Aufgaben:Aufgabe 4.1: Zum „Log Likelihood Ratio”: Unterschied zwischen den Versionen
| (24 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei:P_ID2979__KC_A_4_1_v2.png|right|frame|Betrachtete Kanalmodelle]] | [[Datei:P_ID2979__KC_A_4_1_v2.png|right|frame|Betrachtete Kanalmodelle]] | ||
| − | Zur Interpretation von <i>Log–Likelihood–Verhältnissen</i> (kurz $L$–Werten) gehen wir wie im [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder#Zuverl.C3.A4ssigkeitsinformation_.E2.80.93_Log_Likelihood_Ratio|Theorieteil]] vom <i>Binary Symmetric Channel</i> (BSC) aus. Die englische Bezeichung ist <i>Log Likelihood Ratio</i> (LLR). | + | Zur Interpretation von <i>Log–Likelihood–Verhältnissen</i> (kurz $L$–Werten) gehen wir wie im [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder#Zuverl.C3.A4ssigkeitsinformation_.E2.80.93_Log_Likelihood_Ratio|Theorieteil]] vom <i>Binary Symmetric Channel</i> (BSC) aus. Die englische Bezeichung ist <i>Log Likelihood Ratio</i> (LLR). |
Für die binären Zufallsgrößen am Eingang und Ausgang gelte | Für die binären Zufallsgrößen am Eingang und Ausgang gelte | ||
| Zeile 8: | Zeile 8: | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | Dieses Modell ist in der oberen Grafik dargestellt | + | Dieses Modell ist in der oberen Grafik dargestellt. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt: |
:$${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$ | :$${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$ | ||
:$${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$ | :$${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$ | ||
| − | Die Verfälschungswahrscheinlichkeit $\ | + | Die Verfälschungswahrscheinlichkeit $\varepsilon$ ist der entscheidende Parameter des BSC–Modells. |
| − | Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ das <i>Log Likelihood Ratio</i> (LLR) zu betrachten. | + | Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ das <i>Log Likelihood Ratio</i> (LLR) zu betrachten. |
Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition: | Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition: | ||
:$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | :$$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | ||
| − | wobei der Index & | + | wobei der Index $\rm A$ auf die Apriori–Wahrscheinlichkeit hinweist. |
| − | Beispielsweise ergibt sich für ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ das Apriori–LLR $L_{\rm A}(x) = \, | + | Beispielsweise ergibt sich für ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ das Apriori–LLR $L_{\rm A}(x) = \, -1.382$. |
| − | Aus dem BSC–Modell lässt sich zudem der $L$–Wert der bedingten Wahrscheinlichkeiten ${\rm Pr}(y|x)$ in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit $L_{\rm V}(y)$ bezeichnet wird: | + | Aus dem BSC–Modell lässt sich zudem der $L$–Wert der bedingten Wahrscheinlichkeiten ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit $L_{\rm V}(y)$ bezeichnet wird: |
:$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | :$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = | ||
\left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ | \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ | ||
{\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} | {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} | ||
| − | \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0. | + | \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = 0, |
\\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$ | \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$ | ||
| − | Beispielsweise ergibt sich für $\ | + | Beispielsweise ergibt sich für $\varepsilon = 0.1$: |
:$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$ | :$$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$ | ||
| − | Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten ${\rm Pr}(x|y)$, die mit den Vorwärtswahrscheinlichkeiten ${\rm Pr}(y|x)$ sowie den Eingangswahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ über den Satz von Bayes in Zusammenhang stehen. Der entsprechende $L$–Wert wird in dieser Aufgabe mit $L_{\rm R}(y)$ bezeichnet: | + | Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, die mit den Vorwärtswahrscheinlichkeiten ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ sowie den Eingangswahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ über den Satz von Bayes in Zusammenhang stehen. |
| + | |||
| + | Der entsprechende $L$–Wert wird in dieser Aufgabe mit $L_{\rm R}(y)$ bezeichnet: | ||
:$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = | :$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = | ||
{\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$ | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | * Die Aufgabe | + | * Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Soft%E2%80%93in_Soft%E2%80%93out_Decoder| Soft–in Soft–out Decoder]]. |
| − | * In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen $L_{\rm A}, \ L_{\rm V}$ und $L_{\rm R}$ auch auf den | + | * Bezug genommen wird insbesondere auf die Seite [[Kanalcodierung/Soft–in_Soft–out_Decoder#Zuverl.C3.A4ssigkeitsinformation_.E2.80.93_Log_Likelihood_Ratio| Zuverlässigkeitsinformation – Log Likelihood Ratio]]. |
| + | * In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen $L_{\rm A}, \ L_{\rm V}$ und $L_{\rm R}$ auch auf den „2–auf–$M$–Kanal” übertragen werden können. | ||
| + | *Hierzu wählen wir für die Eingangssymbole eine bipolare Betrachtungsweise: „$0$” → „$+1$” sowie „$1$” → „$–1$”. | ||
| + | |||
| Zeile 46: | Zeile 59: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Wie hängen die bedingten Wahrscheinlichkeiten zweier Zufallsgrößen $A$ und $B$ zusammen? |
| − | |type=" | + | |type="()"} |
| − | + | + | - ${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A)$, |
| − | - | + | - ${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm}B) = {\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm} A) \cdot {\rm Pr}(B) / {\rm Pr}(A)$, |
| + | + ${\rm Pr}(A\hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm}A) \cdot {\rm Pr}(A) / {\rm Pr}(B)$. | ||
| + | |||
| + | {Welche Gleichung gilt für den Binärkanal mit den Wahrscheinlichkeiten ${\rm Pr}(A) = {\rm Pr}(x = 0)$ und ${\rm Pr}(B) = {\rm Pr}(y = 0)$? | ||
| + | |type="()"} | ||
| + | + ${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)$, | ||
| + | - ${\rm Pr}(x = 0 | y = 0) = {\rm Pr}(y = 0 | x = 0) \cdot {\rm Pr}(y = 0) / {\rm Pr}(x = 0)$. | ||
| − | { | + | {Unter welchen Voraussetzungen gilt für das Rückschluss–LLR für alle möglichen Ausgangswerte $y ∈ \{0, \, 1\}$: <br> $L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x)$ bzw. $L_{\rm R}(y) = L_{\rm V}(y)$? |
| + | |type="()"} | ||
| + | - Für jede beliebige Eingangsverteilung ${\rm Pr}(x = 0), \ {\rm Pr}(x = 1)$. | ||
| + | + Nur für die Gleichverteilung: $\hspace{0.2cm} {\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2$. | ||
| + | |||
| + | {Das Ausgangssymbol sei $y = 1$. Welches Rückschluss–LLR erhält man mit der Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ bei gleichwahrscheinlichen Symbolen? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $L_{\rm R}(y = 1) = L(x | y = 1) \ = \ ${ -2.26291--2.13109 } |
| + | |||
| + | {Das Ausgangssymbol sei nun $y = 0$. Welches Rückschluss–LLR erhält man für ${\rm Pr}(x = 0) = 0.2$ und $\varepsilon = 0.1$? | ||
| + | |type="{}"} | ||
| + | $L_{\rm R}(y = 0) = L(x | y = 0) \ = \ ${ 0.815 3% } | ||
| + | |||
| + | {Lässt sich das unter '''(3)''' hergeleitete Ergebnis ⇒ $L_{\rm R} = L_{\rm V} + L_{\rm A}$ auch auf den „2–auf–$M$–Kanal” übertragen? | ||
| + | |type="()"} | ||
| + | + Ja. | ||
| + | - Nein. | ||
| + | |||
| + | {Kann man den Zusammenhang auch auf den AWGN–Kanal übertragen? | ||
| + | |type="()"} | ||
| + | + Ja. | ||
| + | - Nein. | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Für die bedingten Wahrscheinlichkeiten gilt nach dem [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit#Bedingte_Wahrscheinlichkeit| Satz von Bayes]] mit der Schnittmenge $A ∩ B$: |
| − | '''(2)''' | + | :$${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, |
| − | '''(3)''' | + | \hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} |
| − | '''(4)''' | + | \Rightarrow \hspace{0.3cm}{\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = |
| − | '''(5)''' | + | {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$ |
| + | |||
| + | Richtig ist der <u>Lösungsvorschlag 3</u>. Im Sonderfall ${\rm Pr}(B) = {\rm Pr}(A)$ wäre auch der Vorschlag 1 richtig. | ||
| + | |||
| + | |||
| + | '''(2)''' Mit $A$ ⇒ „$x = 0$” und $B$ ⇒ „$y = 0$” ergibt sich sofort die Gleichung gemäß <u>Lösungsvorschlag 1</u>: | ||
| + | :$${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = | ||
| + | {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Wir berechnen den $L$–Wert der Rückschlusswahrscheinlichkeiten. Unter der Annahme $y = 0$ gilt: | ||
| + | :$$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= | ||
| + | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)} + | ||
| + | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| + | |||
| + | In gleicher Weise ergibt sich unter der Annahme $y = 1$: | ||
| + | :$$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die beiden Ergebnisse lassen sich mit $y ∈ \{0, \, 1\}$ und | ||
| + | * dem Eingangs–LLR, | ||
| + | :$$L_{\rm A}(x) = | ||
| + | {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}\hspace{0.05cm},$$ | ||
| + | * sowie dem Vorwärts–LLR, | ||
| + | :$$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} | ||
| + | \hspace{0.05cm},$$ | ||
| + | |||
| + | wie folgt zusammenfassen: | ||
| + | :$$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$ | ||
| + | |||
| + | Die Identität $L_{\rm R}(y) ≡ L_{\rm V}(y)$ erfordert $L_{\rm A}(x) = 0$ ⇒ gleichwahrscheinliche Symbole ⇒ <u>Vorschlag 2</u>. | ||
| + | |||
| + | |||
| + | '''(4)''' Der Aufgabenbeschreibung können Sie entnehmen, dass mit der Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ der Ausgangswert $y = 1$ zum Vorwärts–LLR $L_{\rm V}(y = 1) = \, –2.197$ führt. | ||
| + | |||
| + | *Wegen ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$ gilt somit auch: | ||
| + | :$$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(5)''' Bei gleicher Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ unterscheidet sich $L_{\rm V}(y = 0)$ von $L_{\rm V}(y = 1)$ nur durch das Vorzeichen. | ||
| + | *Mit ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ erhält man somit: | ||
| + | :$$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Wie Sie sicher gerne nachprüfen werden, gilt der Zusammenhang $L_{\rm R} = L_{\rm V} + L_{\rm A}$ auch für den „2–auf–$M$–Kanal”, unabhängig vom Umfang $M$ des Ausgangsalphabets ⇒ <u>Antwort Ja</u>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(7)''' Der AWGN–Kanal wird durch den skizzierten „2–auf–$M$–Kanal” mit $M → ∞$ ebenfalls beschrieben ⇒ <u>Antwort Ja</u>. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Aufgaben zu Kanalcodierung|^4.1 Soft–in Soft–out Decoder^]] | [[Category:Aufgaben zu Kanalcodierung|^4.1 Soft–in Soft–out Decoder^]] | ||
Aktuelle Version vom 4. Juli 2019, 15:28 Uhr
Zur Interpretation von Log–Likelihood–Verhältnissen (kurz $L$–Werten) gehen wir wie im Theorieteil vom Binary Symmetric Channel (BSC) aus. Die englische Bezeichung ist Log Likelihood Ratio (LLR).
Für die binären Zufallsgrößen am Eingang und Ausgang gelte
- $$x \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm},\hspace{0.25cm}y \in \{0\hspace{0.05cm}, 1\} \hspace{0.05cm}. $$
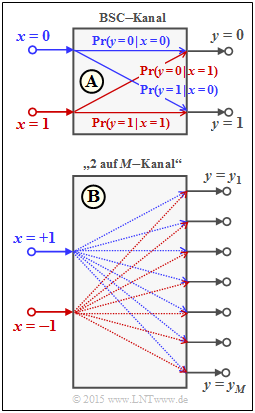
Dieses Modell ist in der oberen Grafik dargestellt. Für die bedingten Wahrscheinlichkeiten in Vorwärtsrichtung gilt:
- $${\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 1) = \varepsilon \hspace{0.05cm},$$
- $${\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} {\rm Pr}(y = 1\hspace{0.05cm}|\hspace{0.05cm} x = 1) = 1-\varepsilon \hspace{0.05cm}.$$
Die Verfälschungswahrscheinlichkeit $\varepsilon$ ist der entscheidende Parameter des BSC–Modells.
Bezüglich der Wahrscheinlichkeitsverteilung am Eingang ist es zweckmäßig, anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ das Log Likelihood Ratio (LLR) zu betrachten.
Für dieses gilt bei der hier verwendeten unipolaren Betrachtungsweise per Definition:
- $$L_{\rm A}(x)={\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)}{{\rm Pr}(x = 1)}\hspace{0.05cm},$$
wobei der Index $\rm A$ auf die Apriori–Wahrscheinlichkeit hinweist.
Beispielsweise ergibt sich für ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ {\rm Pr}(x = 1) = 0.8$ das Apriori–LLR $L_{\rm A}(x) = \, -1.382$.
Aus dem BSC–Modell lässt sich zudem der $L$–Wert der bedingten Wahrscheinlichkeiten ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ in Vorwärtsrichtung ermitteln, der in der vorliegenden Aufgabe auch mit $L_{\rm V}(y)$ bezeichnet wird:
- $$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 0)}{{\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x = 1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} [(1 - \varepsilon)/\varepsilon]\\ {\rm ln} \hspace{0.15cm} [\varepsilon/(1 - \varepsilon)] \end{array} \right.\hspace{0.15cm} \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = 0, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = 1. \\ \end{array}$$
Beispielsweise ergibt sich für $\varepsilon = 0.1$:
- $$L_{\rm V}(y = 0) = +2.197\hspace{0.05cm}, \hspace{0.3cm}L_{\rm V}(y = 1) = -2.197\hspace{0.05cm}.$$
Von besonderer Bedeutung für die Codierungstheorie sind die Rückschlusswahrscheinlichkeiten ${\rm Pr}(x\hspace{0.05cm}|\hspace{0.05cm}y)$, die mit den Vorwärtswahrscheinlichkeiten ${\rm Pr}(y\hspace{0.05cm}|\hspace{0.05cm}x)$ sowie den Eingangswahrscheinlichkeiten ${\rm Pr}(x = 0)$ und ${\rm Pr}(x = 1)$ über den Satz von Bayes in Zusammenhang stehen.
Der entsprechende $L$–Wert wird in dieser Aufgabe mit $L_{\rm R}(y)$ bezeichnet:
- $$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0)\hspace{0.05cm}|\hspace{0.05cm}y)}{{\rm Pr}(x = 1)\hspace{0.05cm}|\hspace{0.05cm}y)} \hspace{0.05cm} .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Soft–in Soft–out Decoder.
- Bezug genommen wird insbesondere auf die Seite Zuverlässigkeitsinformation – Log Likelihood Ratio.
- In den letzten Teilaufgaben ist zu klären, ob die gefundenen Zusammenhänge zwischen $L_{\rm A}, \ L_{\rm V}$ und $L_{\rm R}$ auch auf den „2–auf–$M$–Kanal” übertragen werden können.
- Hierzu wählen wir für die Eingangssymbole eine bipolare Betrachtungsweise: „$0$” → „$+1$” sowie „$1$” → „$–1$”.
Fragebogen
Musterlösung
- $${\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(A)}\hspace{0.05cm}, \hspace{0.3cm} {\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Pr}(A \hspace{0.05cm}|\hspace{0.05cm} B) = {\rm Pr}(B \hspace{0.05cm}|\hspace{0.05cm} A) \cdot \frac{{\rm Pr}(A)}{{\rm Pr}(B)}\hspace{0.05cm}.$$
Richtig ist der Lösungsvorschlag 3. Im Sonderfall ${\rm Pr}(B) = {\rm Pr}(A)$ wäre auch der Vorschlag 1 richtig.
(2) Mit $A$ ⇒ „$x = 0$” und $B$ ⇒ „$y = 0$” ergibt sich sofort die Gleichung gemäß Lösungsvorschlag 1:
- $${\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm} y = 0) = {\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm} x = 0) \cdot \frac{{\rm Pr}(x = 0)}{{\rm Pr}(y = 0)}\hspace{0.05cm}.$$
(3) Wir berechnen den $L$–Wert der Rückschlusswahrscheinlichkeiten. Unter der Annahme $y = 0$ gilt:
- $$L_{\rm R}(y= 0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x = 0\hspace{0.05cm}|\hspace{0.05cm}y=0)}{{\rm Pr}(x = 1\hspace{0.05cm}|\hspace{0.05cm}y=0)} = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) \cdot {\rm Pr}(x = 0) / {\rm Pr}(y = 0)}{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)\cdot {\rm Pr}(x = 1) / {\rm Pr}(y = 0)} $$
- $$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0)= {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y = 0\hspace{0.05cm}|\hspace{0.05cm}x = 1)} + {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}$$
- $$\Rightarrow \hspace{0.3cm} L_{\rm R}(y= 0) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 0) = L_{\rm V}(y= 0) + L_{\rm A}(x)\hspace{0.05cm}.$$
In gleicher Weise ergibt sich unter der Annahme $y = 1$:
- $$L_{\rm R}(y= 1) = L(x\hspace{0.05cm}|\hspace{0.05cm}y= 1) = L_{\rm V}(y= 1) + L_{\rm A}(x)\hspace{0.05cm}.$$
Die beiden Ergebnisse lassen sich mit $y ∈ \{0, \, 1\}$ und
- dem Eingangs–LLR,
- $$L_{\rm A}(x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x=0) }{{\rm Pr}(x = 1)}\hspace{0.05cm},$$
- sowie dem Vorwärts–LLR,
- $$L_{\rm V}(y) = L(y\hspace{0.05cm}|\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x=0) }{{\rm Pr}(y \hspace{0.05cm}|\hspace{0.05cm}x = 1)} \hspace{0.05cm},$$
wie folgt zusammenfassen:
- $$L_{\rm R}(y) = L(x\hspace{0.05cm}|\hspace{0.05cm}y) = L_{\rm V}(y) + L_{\rm A}(x)\hspace{0.05cm}.$$
Die Identität $L_{\rm R}(y) ≡ L_{\rm V}(y)$ erfordert $L_{\rm A}(x) = 0$ ⇒ gleichwahrscheinliche Symbole ⇒ Vorschlag 2.
(4) Der Aufgabenbeschreibung können Sie entnehmen, dass mit der Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ der Ausgangswert $y = 1$ zum Vorwärts–LLR $L_{\rm V}(y = 1) = \, –2.197$ führt.
- Wegen ${\rm Pr}(x = 0) = 1/2 \ \Rightarrow \ L_{\rm A}(x) = 0$ gilt somit auch:
- $$L_{\rm R}(y = 1) = L_{\rm V}(y = 1) \hspace{0.15cm}\underline{= -2.197}\hspace{0.05cm}.$$
(5) Bei gleicher Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ unterscheidet sich $L_{\rm V}(y = 0)$ von $L_{\rm V}(y = 1)$ nur durch das Vorzeichen.
- Mit ${\rm Pr}(x = 0) = 0.2 \ \Rightarrow \ L_{\rm A}(x) = \, -1.382$ erhält man somit:
- $$L_{\rm R}(y = 0) = (+)2.197 - 1.382 \hspace{0.15cm}\underline{=+0.815}\hspace{0.05cm}.$$
(6) Wie Sie sicher gerne nachprüfen werden, gilt der Zusammenhang $L_{\rm R} = L_{\rm V} + L_{\rm A}$ auch für den „2–auf–$M$–Kanal”, unabhängig vom Umfang $M$ des Ausgangsalphabets ⇒ Antwort Ja.
(7) Der AWGN–Kanal wird durch den skizzierten „2–auf–$M$–Kanal” mit $M → ∞$ ebenfalls beschrieben ⇒ Antwort Ja.