Aufgaben:Aufgabe 3.4: GMSK–Modulation: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1229__Bei_A_3_4.png|right|frame|GMSK-Modulation]] | + | [[Datei:P_ID1229__Bei_A_3_4.png|right|frame|Verschiedene Signale der GMSK-Modulation]] |
| − | Das bei GSM eingesetzte Modulationsverfahren ist bekanntlich | + | Das bei GSM eingesetzte Modulationsverfahren ist bekanntlich ''Gaussian Minimum Shift Keying'', abgekürtzt $\rm GMSK$. Dabei handelt es sich um eine Art von '' Frequency Shift Keying'' (FSK) mit kontinuierlicher Phasenanpassung $(\rm CP–FSK)$, bei der |
| − | *der Modulationsindex kleinstmöglich ist, um die Orthogonalitätsbedingung noch zu erfüllen | + | *der Modulationsindex kleinstmöglich ist, um die Orthogonalitätsbedingung noch zu erfüllen <br> $h = 0.5$ ⇒ ''Minimum Shift Keying'', |
| − | *ein Gaußtiefpass mit Impulsantwort $h_{\rm G}(t)$ vor dem FSK–Modulator eingebracht ist, um noch weiter Bandbreite einzusparen. | + | *ein Gaußtiefpass mit Impulsantwort $h_{\rm G}(t)$ vor dem FSK–Modulator eingebracht ist, <br>um noch weiter Bandbreite einzusparen. |
| − | + | Die Grafik verdeutlicht den Sachverhalt: | |
| − | Die digitale Nachricht wird durch die Amplitudenkoeffizienten $a_{\nu} ∈ ±1$ repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete Folge für die Teilaufgabe (3) vorausgesetzt wird. | + | *Die digitale Nachricht wird durch die Amplitudenkoeffizienten $a_{\nu} ∈ ±1$ repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete (rote) Folge für die Teilaufgabe '''(3)''' vorausgesetzt wird. |
| − | Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer $T_{\rm B} = T$: | + | *Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer $T_{\rm B} = T$: |
:$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$ | :$$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$ | ||
| − | Damit ergibt sich für das Rechtecksignal: | + | :Damit ergibt sich für das Rechtecksignal: |
:$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | Der Gaußtiefpass ist durch Frequenzgang bzw. Impulsantwort gegeben: | + | *Der Gaußtiefpass ist durch seinen Frequenzgang bzw. seine Impulsantwort gegeben: |
| − | :$$H_{\rm G}(f) = {\rm e}^{-\pi\cdot | + | :$$H_{\rm G}(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}[f/(2 f_{\rm G})]^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$ |
| − | wobei die systemtheoretische Grenzfrequenz $f_{\rm G}$ verwendet wird. In der GSM–Spezifikation wird aber die $3 \rm dB$–Grenzfrequenz mit $f_{\rm | + | :wobei die systemtheoretische Grenzfrequenz $f_{\rm G}$ verwendet wird. In der GSM–Spezifikation wird aber die $3 \hspace{0.05cm}\rm dB$–Grenzfrequenz mit $f_{\rm 3\hspace{0.05cm} dB} = 0.3/T$ angegeben. Daraus kann $f_{\rm G}$ direkt berechnet werden. |
| − | Das Signal nach dem Gaußtiefpass lautet somit: | + | *Das Signal nach dem Gaußtiefpass lautet somit: |
:$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$ | :$$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$ | ||
| − | Hierbei wird $g(t)$ als Frequenzimpuls bezeichnet. Für diesen gilt: | + | :Hierbei wird $g(t)$ als Frequenzimpuls bezeichnet. Für diesen gilt: |
:$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$ | :$$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$ | ||
| − | Mit dem tiefpassgefilterten Signal $q_{\rm G}(t)$, der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $\Delta f_{\rm A}$ kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden: | + | *Mit dem tiefpassgefilterten Signal $q_{\rm G}(t)$, der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $\Delta f_{\rm A}$ kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden: |
:$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$ | :$$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$ | ||
| − | Verwenden Sie für Ihre Berechnungen die beispielhaften Werte $f_{\rm T} = 900 \ \rm MHz$ und $\Delta f_{\rm A} = 68 \ \rm kHz$. | + | :Verwenden Sie für Ihre Berechnungen die beispielhaften Werte $f_{\rm T} = 900 \ \rm MHz$ und $\Delta f_{\rm A} = 68 \ \rm kHz$. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | |||
| + | [[Datei:P_ID1230__Bei_A_3_4b.png|right|frame|Tabelle der Gaußschen Fehlerfunktion]] | ||
| + | *Diese Aufgabe gehört zum Kapitel [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle|Funkschnittstelle]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Beispiele_von_Nachrichtensystemen/Funkschnittstelle#Gaussian_Minimum_Shift_Keying_.28GMSK.29|Gaussian Minimum Shift Keying]] | ||
| + | |||
| + | *Verwenden Sie zur Lösung dieser Aufgabe das Gaußintegral (siehe nebenstehende Tabelle): | ||
| + | :$$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$ | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {In welchem Bereich kann die Augenblicksfrequenz $f_{\rm A}(t)$ schwanken? Welche Voraussetzungen müssen dafür erfüllt sein? | ||
| + | |type="{}"} | ||
| + | ${\rm Max} \ \big [f_{\rm A}(t) \big ] \ = \ $ { 900.068 3% } | ||
| + | |||
| + | {Welche systemtheoretische Grenzfrequenz des Gaußtiefpasses ergibt sich aus der Forderung $f_{\rm 3\hspace{0.05cm} dB} \cdot T = 0.3$? | ||
| + | |type="{}"} | ||
| + | $f_{\rm G} \cdot T \ = \ $ { 0.45 3% } | ||
| + | |||
| + | {Berechnen Sie den Frequenzimpuls $g(t)$ unter Verwendung der Funktion $\Phi (x)$. Wie groß ist der Impulswert $g(t = 0)$? | ||
| + | |type="{}"} | ||
| + | $g(t = 0) \ = \ $ { 0.737 3% } | ||
| + | |||
| + | {Welcher Wert ergibt sich für $q_{\rm G}(t = 3T)$, wenn alle Koeffizienten außer $a_{3} = -1$ weiterhin $a_{\nu \neq 3} = +1$ sind? Wie groß ist hier $f_{\rm A}(t = 3T)$? | ||
| + | |type="{}"} | ||
| + | $q_{\rm G}(t = 3T) \ = \ $ { -0.48822--0.45978 } | ||
| − | { | + | {Berechnen Sie die Impulswerte $g(t = ±T)$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ g(t = ±T) \ = \ $ { 0.131 3% } |
| + | {Wie groß ist der maximale Betrag von $q_{\rm G}(t)$ bei alternierenden Koeffizienten? Berücksichtigen Sie, dass $g(t ≥ 2 T) \approx 0$ ist. | ||
| + | |type="{}"} | ||
| + | ${\rm Max} \ |q_{\rm G}(t)| \ = \ $ { 0.475 3% } | ||
| Zeile 61: | Zeile 86: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Wenn alle Amplitudenkoeffizienten $a_{\nu}$ gleich $+1$ sind, ist $q_{\rm R}(t) = 1$ eine Konstante. |
| − | '''(2)''' | + | *Der Gaußtiefpass hat deshalb keinen Einfluss und es ergibt sich $q_{\rm G}(t) = 1$. |
| − | '''(3)''' | + | *Die maximale Frequenz ist somit |
| − | '''(4)''' | + | :$${\rm Max}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$ |
| − | '''(5)''' | + | |
| − | '''( | + | *Das Minimum der Augenblicksfrequenz ergibt sich, wenn alle Amplitudenkoeffizienten negativ sind: |
| − | '''( | + | :$${\rm Min}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$ |
| + | *In diesem Fall ist $q_{\rm R}(t) = q_{\rm G}(t) = -1$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Diejenige Frequenz, bei der die logarithmierte Leistungsübertragungsfunktion gegenüber $f = 0$ um $3 \ \rm dB$ kleiner ist, bezeichnet man als die $3\hspace{0.05cm}\rm dB$–Grenzfrequenz. | ||
| + | *Diese lässt sich auch wie folgt ausdrücken: | ||
| + | :$$\frac {|H(f = f_{\rm 3\hspace{0.05cm}dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Insbesondere gilt für den Gaußtiefpass wegen $H(f = 0) = 1$: | ||
| + | :$$H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$ | ||
| + | *Die numerische Auswertung führt auf $f_{\rm G} \approx 1.5 \cdot f_{\rm 3\hspace{0.05cm}dB}$. | ||
| + | *Aus $f_{\rm 3\hspace{0.05cm}dB} \cdot T = 0.3$ folgt somit $f_{\rm G} \cdot T \hspace{0.15cm}\underline{\approx 0.45}$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Der Frequenzimpuls ergibt sich aus der Faltung von Rechteckfunktion $g_{\rm R}(t)$ und Impulsantwort $h_{\rm G}(t)$: | ||
| + | :$$g(t) = g_{\rm R} (t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot \int \limits^{t + T/2} _{t - T/2} {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot \tau)^2}\,{\rm d}\tau \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Mit der Substitution $u^{2 } = 8π \cdot f_{\rm G}^{2} \cdot \tau^{2}$ und der Funktion $\phi (x)$ kann hierfür auch geschrieben werden: | ||
| + | :$$g(t) \ = \ \frac {1}{\sqrt{2 \pi}} \cdot \int \limits^{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2)} _{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)} {\rm e}^{-u^2/2}\,{\rm d}u = \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2))- \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)) \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Für die Zeit $t = 0$ gilt unter Berücksichtigung von $\phi (-x) = 1 - \phi (x)$ und $f_{\rm G} \cdot T = 0.45$: | ||
| + | :$$g(t = 0) \ = \ \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(-\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)= 2 \cdot \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)-1 \approx 2 \cdot \phi(1.12)-1 \hspace{0.15cm} \underline {= 0.737} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Mit $a_{3} = +1$ würde sich $q_{\rm G}(t = 3 T) = 1$ ergeben. Aufgrund der Linearität gilt somit: | ||
| + | :$$q_{\rm G}(t = 3 T ) = 1 - 2 \cdot g(t = 0)= 1 - 2 \cdot 0.737 \hspace{0.15cm} \underline {= -0.474} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Mit dem Ergebnis der Teilaufgabe '''(3)''' und $f_{\rm G} \cdot T = 0.45$ erhält man: | ||
| + | :$$g(t = T) \ = \ \phi(3 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T) \approx \ \phi(3.36)-\phi(1.12) = 0.999 - 0.868 \hspace{0.15cm} \underline { = 0.131} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(6)''' Bei der alternierenden Folge sind aus Symmetriegründen die Beträge $|q_{\rm G}(\nu \cdot T)|$ bei allen Vielfachen der Bitdauer $T$ alle gleich. | ||
| + | *Alle Zwischenwerte bei $t \neq \nu · T$ sind kleiner. | ||
| + | *Unter Berücksichtigung von $g(t ≥ 2T) \approx 0$ wird jeder einzelne Impulswert $g(0)$ durch den vorangegangenen Impuls mit $g(t = T)$ verkleinert, zusätzlich vom nachfolgenden mit $g(t = -T)$. | ||
| + | *Es ergeben sich also Impulsinterferenzen und man erhält: | ||
| + | :$${\rm Max} \hspace{0.08cm}q_{\rm G}(t) = g(0) - 2 \cdot g(T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 8. August 2019, 15:14 Uhr
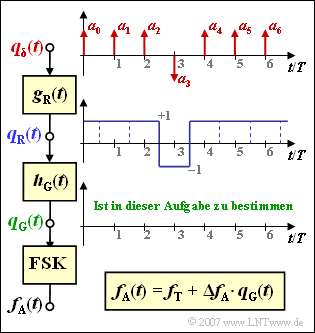
Das bei GSM eingesetzte Modulationsverfahren ist bekanntlich Gaussian Minimum Shift Keying, abgekürtzt $\rm GMSK$. Dabei handelt es sich um eine Art von Frequency Shift Keying (FSK) mit kontinuierlicher Phasenanpassung $(\rm CP–FSK)$, bei der
- der Modulationsindex kleinstmöglich ist, um die Orthogonalitätsbedingung noch zu erfüllen
$h = 0.5$ ⇒ Minimum Shift Keying, - ein Gaußtiefpass mit Impulsantwort $h_{\rm G}(t)$ vor dem FSK–Modulator eingebracht ist,
um noch weiter Bandbreite einzusparen.
Die Grafik verdeutlicht den Sachverhalt:
- Die digitale Nachricht wird durch die Amplitudenkoeffizienten $a_{\nu} ∈ ±1$ repräsentiert, die einem Diracpuls beaufschlagt sind. Anzumerken ist, dass die eingezeichnete (rote) Folge für die Teilaufgabe (3) vorausgesetzt wird.
- Der Rechteckimpuls sei dimensionslos, symmetrisch und besitze die GSM–Bitdauer $T_{\rm B} = T$:
- $$g_{\rm R}(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |\hspace{0.05cm} t \hspace{0.05cm}| < T/2 \hspace{0.05cm}, \\ |\hspace{0.05cm} t \hspace{0.05cm}| > T/2 \hspace{0.05cm}. \\ \end{array}$$
- Damit ergibt sich für das Rechtecksignal:
- $$q_{\rm R} (t) = q_{\rm \delta} (t) \star g_{\rm R}(t) = \sum_{\nu} a_{\nu}\cdot g_{\rm R}(t - \nu \cdot T)\hspace{0.05cm}.$$
- Der Gaußtiefpass ist durch seinen Frequenzgang bzw. seine Impulsantwort gegeben:
- $$H_{\rm G}(f) = {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}[f/(2 f_{\rm G})]^2} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm G}(t) = 2 f_{\rm G} \cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(2 f_{\rm G}\cdot t)^2}\hspace{0.05cm},$$
- wobei die systemtheoretische Grenzfrequenz $f_{\rm G}$ verwendet wird. In der GSM–Spezifikation wird aber die $3 \hspace{0.05cm}\rm dB$–Grenzfrequenz mit $f_{\rm 3\hspace{0.05cm} dB} = 0.3/T$ angegeben. Daraus kann $f_{\rm G}$ direkt berechnet werden.
- Das Signal nach dem Gaußtiefpass lautet somit:
- $$q_{\rm G} (t) = q_{\rm R} (t) \star h_{\rm G}(t) = \sum_{\nu} a_{\nu}\cdot g(t - \nu \cdot T)\hspace{0.05cm}.$$
- Hierbei wird $g(t)$ als Frequenzimpuls bezeichnet. Für diesen gilt:
- $$g(t) = q_{\rm R} (t) \star h_{\rm G}(t) \hspace{0.05cm}.$$
- Mit dem tiefpassgefilterten Signal $q_{\rm G}(t)$, der Trägerfrequenz $f_{\rm T}$ und dem Frequenzhub $\Delta f_{\rm A}$ kann somit für die Augenblicksfrequenz am Ausgang des FSK–Modulators geschrieben werden:
- $$f_{\rm A}(t) = f_{\rm T} + \Delta f_{\rm A} \cdot q_{\rm G} (t)\hspace{0.05cm}.$$
- Verwenden Sie für Ihre Berechnungen die beispielhaften Werte $f_{\rm T} = 900 \ \rm MHz$ und $\Delta f_{\rm A} = 68 \ \rm kHz$.
Hinweise:
- Diese Aufgabe gehört zum Kapitel Funkschnittstelle.
- Bezug genommen wird insbesondere auf die Seite Gaussian Minimum Shift Keying
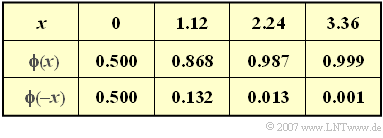
- Verwenden Sie zur Lösung dieser Aufgabe das Gaußintegral (siehe nebenstehende Tabelle):
- $$\phi(x) =\frac {1}{\sqrt{2 \pi}} \cdot \int^{x} _{-\infty} {\rm e}^{-u^2/2}\,{\rm d}u \hspace{0.05cm}.$$
Fragebogen
Musterlösung
- Der Gaußtiefpass hat deshalb keinen Einfluss und es ergibt sich $q_{\rm G}(t) = 1$.
- Die maximale Frequenz ist somit
- $${\rm Max}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} + \Delta f_{\rm A} \hspace{0.15cm} \underline {= 900.068\,{\rm MHz}} \hspace{0.05cm}.$$
- Das Minimum der Augenblicksfrequenz ergibt sich, wenn alle Amplitudenkoeffizienten negativ sind:
- $${\rm Min}\hspace{0.05cm}[f_{\rm A}(t)] = f_{\rm T} - \Delta f_{\rm A} \hspace{0.15cm} \underline { = 899.932\,{\rm MHz}} \hspace{0.05cm}$$
- In diesem Fall ist $q_{\rm R}(t) = q_{\rm G}(t) = -1$.
(2) Diejenige Frequenz, bei der die logarithmierte Leistungsübertragungsfunktion gegenüber $f = 0$ um $3 \ \rm dB$ kleiner ist, bezeichnet man als die $3\hspace{0.05cm}\rm dB$–Grenzfrequenz.
- Diese lässt sich auch wie folgt ausdrücken:
- $$\frac {|H(f = f_{\rm 3\hspace{0.05cm}dB})|}{|H(f = 0)|}= \frac{1}{\sqrt{2}} \hspace{0.05cm}.$$
- Insbesondere gilt für den Gaußtiefpass wegen $H(f = 0) = 1$:
- $$H(f = f_{\rm 3dB})= {\rm e}^{-\pi\cdot ({f_{\rm 3dB}}/{2 f_{\rm G}})^2} = \frac{1}{\sqrt{2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}(\frac{f_{\rm 3dB}}{2 f_{\rm G}})^2 = \frac{{\rm ln}\hspace{0.1cm}\sqrt{2}}{\pi} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm G} = \sqrt{\frac{\pi}{4 \cdot {\rm ln}\hspace{0.1cm}\sqrt{2}}}\cdot f_{\rm 3dB}\hspace{0.05cm}.$$
- Die numerische Auswertung führt auf $f_{\rm G} \approx 1.5 \cdot f_{\rm 3\hspace{0.05cm}dB}$.
- Aus $f_{\rm 3\hspace{0.05cm}dB} \cdot T = 0.3$ folgt somit $f_{\rm G} \cdot T \hspace{0.15cm}\underline{\approx 0.45}$.
(3) Der Frequenzimpuls ergibt sich aus der Faltung von Rechteckfunktion $g_{\rm R}(t)$ und Impulsantwort $h_{\rm G}(t)$:
- $$g(t) = g_{\rm R} (t) \star h_{\rm G}(t) = 2 f_{\rm G} \cdot \int \limits^{t + T/2} _{t - T/2} {\rm e}^{-\pi\cdot (2 f_{\rm G}\cdot \tau)^2}\,{\rm d}\tau \hspace{0.05cm}.$$
- Mit der Substitution $u^{2 } = 8π \cdot f_{\rm G}^{2} \cdot \tau^{2}$ und der Funktion $\phi (x)$ kann hierfür auch geschrieben werden:
- $$g(t) \ = \ \frac {1}{\sqrt{2 \pi}} \cdot \int \limits^{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2)} _{2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)} {\rm e}^{-u^2/2}\,{\rm d}u = \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t + T/2))- \phi(2 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot(t - T/2)) \hspace{0.05cm}.$$
- Für die Zeit $t = 0$ gilt unter Berücksichtigung von $\phi (-x) = 1 - \phi (x)$ und $f_{\rm G} \cdot T = 0.45$:
- $$g(t = 0) \ = \ \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(-\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)= 2 \cdot \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T)-1 \approx 2 \cdot \phi(1.12)-1 \hspace{0.15cm} \underline {= 0.737} \hspace{0.05cm}.$$
(4) Mit $a_{3} = +1$ würde sich $q_{\rm G}(t = 3 T) = 1$ ergeben. Aufgrund der Linearität gilt somit:
- $$q_{\rm G}(t = 3 T ) = 1 - 2 \cdot g(t = 0)= 1 - 2 \cdot 0.737 \hspace{0.15cm} \underline {= -0.474} \hspace{0.05cm}.$$
(5) Mit dem Ergebnis der Teilaufgabe (3) und $f_{\rm G} \cdot T = 0.45$ erhält man:
- $$g(t = T) \ = \ \phi(3 \cdot \sqrt{2 \pi} \cdot f_{\rm G} \cdot T)- \phi(\sqrt{2 \pi} \cdot f_{\rm G} \cdot T) \approx \ \phi(3.36)-\phi(1.12) = 0.999 - 0.868 \hspace{0.15cm} \underline { = 0.131} \hspace{0.05cm}.$$
(6) Bei der alternierenden Folge sind aus Symmetriegründen die Beträge $|q_{\rm G}(\nu \cdot T)|$ bei allen Vielfachen der Bitdauer $T$ alle gleich.
- Alle Zwischenwerte bei $t \neq \nu · T$ sind kleiner.
- Unter Berücksichtigung von $g(t ≥ 2T) \approx 0$ wird jeder einzelne Impulswert $g(0)$ durch den vorangegangenen Impuls mit $g(t = T)$ verkleinert, zusätzlich vom nachfolgenden mit $g(t = -T)$.
- Es ergeben sich also Impulsinterferenzen und man erhält:
- $${\rm Max} \hspace{0.08cm}q_{\rm G}(t) = g(0) - 2 \cdot g(T) = 0.737 - 2 \cdot 0.131 \hspace{0.15cm} \underline {= 0.475 }\hspace{0.05cm}.$$