Signaldarstellung/Analytisches Signal und zugehörige Spektralfunktion: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (39 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Definition im Frequenzbereich== | ==Definition im Frequenzbereich== | ||
| + | <br> | ||
| + | Wir betrachten ein reelles bandpassartiges Signal $x(t)$ mit dem dazugehörigen Bandpass–Spektrum $X(f)$, das bezüglich des Frequenznullpunktes einen geraden Real– und einen ungeraden Imaginärteil besitzt. Es wird vorausgesetzt, dass die Trägerfrequenz $f_{\rm T}$ sehr viel größer als die Bandbreite des Bandpass–Signals $x(t)$ ist. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Das zum physikalischen Signal $x(t)$ gehörige $\text{analytische Signal}$ $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt: | ||
| + | [[Datei:Sig_T_4_2_S1a_Version2.png|right|frame|Analytisches Signal im Frequenzbereich]] | ||
| + | :$$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot | ||
| + | X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$ | ||
| − | { | + | Die so genannte $\text{Signumfunktion}$ ist dabei für positive Frequenzwerte gleich $+1$ und für negative $f$–Werte gleich $-1$. |
| − | + | *Der (beidseitige) Grenzwert liefert $\sign(0) = 0$. | |
| − | + | *Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt. | |
| − | $$ | ||
| − | |||
| − | |||
| − | + | Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$: | |
| − | + | Das tatsächliche Bandpass–Spektrum $X(f)$ wird | |
| − | |||
*bei den positiven Frequenzen verdoppelt, und | *bei den positiven Frequenzen verdoppelt, und | ||
| − | *bei den negativen Frequenzen zu Null gesetzt. | + | *bei den negativen Frequenzen zu Null gesetzt.}} |
| − | + | <br clear=all> | |
| + | [[Datei:P_ID711__Sig_T_4_2_S1b_neu.png|right|frame|Spektrum $X(f)$ und Spektrum $X_{+}(f)$ des analytischen Signals]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ | ||
| − | + | Die Grafik zeigt | |
| − | + | *links das diskrete und komplexe Spektrum $X(f)$ des Bandpass–Signals | |
| − | $$x(t) = 4\hspace{0.05cm}{\rm V} | + | :$$x(t) = 4\hspace{0.05cm}{\rm V} |
\cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} | \cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} | ||
| − | \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t) | + | \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t),$$ |
| − | + | *rechts das (ebenfalls diskrete, komplexe) Spektrum des analytischen Signals $x_{+}(t)$. | |
| − | + | }} | |
==Allgemeingültige Berechnungsvorschrift im Zeitbereich== | ==Allgemeingültige Berechnungsvorschrift im Zeitbereich== | ||
| + | <br> | ||
| + | [[Datei:Sig_T_4_2_S2a_Version2.png|right|frame|Zur anschaulichen Erklärung des analytischen Signals]] | ||
| + | Wir betrachten nun das Spektrum $X_+(f)$ des analytischen Signals etwas genauer und teilen dieses in einen bezüglich $f = 0$ geraden Anteil $X_{\rm +g}(f)$ und einen ungeraden Anteil $X_{\rm +u}(f)$ auf: | ||
| + | :$$X_+(f) = X_{\rm +g}(f) + X_{\rm +u}(f).$$ | ||
| + | Alle diese Spektren sind im allgemeinen komplex. | ||
| − | + | Berücksichtigt man den [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Zuordnungssatz]] der Fouriertransformation, so sind anhand der Grafik folgende Aussagen möglich: | |
| − | + | *Der gerade Anteil $X_{\rm +g}(f)$ von $X_{+}(f)$ führt nach der Fouriertransformation zu einem reellen Zeitsignal, der ungerade Anteil $X_{\rm +u}(f)$ zu einem imaginären. | |
| − | Berücksichtigt man den Zuordnungssatz der Fouriertransformation, so sind anhand der Grafik folgende Aussagen möglich: | + | *Es ist offensichtlich, dass $X_{\rm +g}(f)$ gleich dem tatsächlichen Fourierspektrum $X(f)$ und damit der Realteil von $x_{\rm +g}(t)$ gleich dem vorgegebenen Signal $x(t)$ mit Bandpasseigenschaften ist. |
| − | *Der gerade Anteil $X_{+g}(f)$ von $X_{+}(f)$ führt nach der Fouriertransformation zu einem | + | *Bezeichnen wir den Imaginärteil mit $y(t)$, so lautet das analytische Signal: |
| − | *Es ist offensichtlich, dass $X_{+g}(f)$ gleich dem tatsächlichen Fourierspektrum $X(f)$ und damit der Realteil von $x_{+g}(t)$ gleich dem vorgegebenen | + | :$$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$ |
| − | *Bezeichnen wir den Imaginärteil mit y(t), so lautet das analytische Signal: | + | *Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Zuordnungssatz]] gilt somit für die Spektralfunktion des Imaginärteils: |
| − | $$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$ | + | :$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) |
| − | *Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm |
| − | $${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) | + | sign}(f)}{ {\rm j}}\cdot X(f).$$ |
| − | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{ {\rm | + | *Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungsoperation]], und man erhält: |
| − | sign}(f)}{{\rm j}}\cdot X(f).$$ | + | :$$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star |
| − | *Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die Faltungsoperation, und man erhält: | + | \hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot |
| − | $$y(t) = \frac{1}{{\rm \pi} t} \hspace{0.05cm}\star | + | \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - |
| − | \hspace{0.05cm}x(t) = \frac{1}{{\rm \pi}} \cdot | ||
| − | \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{{t - | ||
\tau}}\hspace{0.15cm} {\rm d}\tau.$$ | \tau}}\hspace{0.15cm} {\rm d}\tau.$$ | ||
| + | ==Darstellung mit der Hilberttransformation== | ||
| + | <br> | ||
| + | An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen, die im Buch [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Lineare zeitinvariante Systeme]] genauer behandelt wird. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Für die $\text{Hilberttransformierte}$ $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt: | ||
| + | |||
| + | :$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot | ||
| + | \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - | ||
| + | \tau} }\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | + | *Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des [https://de.wikipedia.org/wiki/Cauchyscher_Hauptwert Cauchy–Hauptwertsatzes] ausgewertet werden. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *Entsprechend gilt im Frequenzbereich: | |
| − | $$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$ | + | :$$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$}} |
| − | |||
| − | |||
Das Ergebnis der letzten Seite lässt sich mit dieser Definition wie folgt zusammenfassen: | Das Ergebnis der letzten Seite lässt sich mit dieser Definition wie folgt zusammenfassen: | ||
| − | *Man erhält aus dem realen, physikalischen | + | *Man erhält aus dem realen, physikalischen Bandpass–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil entsprechend der Hilberttransformierten hinzufügt: |
| − | $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ | + | :$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ |
| − | *Die Hilberttransformierte $\text{H}\{x(t)\}$ verschwindet nur für | + | *Die Hilberttransformierte $\text{H}\{x(t)\}$ verschwindet nur für den Fall $x(t) = \rm const.$ ⇒ Gleichsignal. Bei allen anderen Signalformen ist das analytische Signal $x_+(t)$ somit stets komplex. |
| − | *Aus dem analytischen Signal $x_+(t)$ kann das | + | *Aus dem analytischen Signal $x_+(t)$ kann das physikalisch Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden: |
| − | $$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$ | + | :$$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$ |
| − | Das Prinzip der Hilbert–Transformation wird durch die | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 2:}$ Das Prinzip der Hilbert–Transformation wird durch die folgende Grafik nochmals verdeutlicht: | |
| − | + | *Nach der linken Darstellung $\rm (A)$ kommt man vom physikalischen Signal $x(t)$ zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil ${\rm j} \cdot y(t)$ hinzufügt. | |
| + | *$y(t) = {\rm H}\left\{x(t)\right\}$ ist eine reelle Funktion, die sich am einfachsten im Spektralbereich durch Multiplikation des Spektrums $X(f)$ mit $- {\rm j} \cdot \sign(f)$ angeben lässt. | ||
| + | [[Datei:P_ID2729__Sig_T_4_2_S2b_neu.png|right|frame|Zur Verdeutlichung der Hilbert–Transformierten]] | ||
| + | <br><br><br> | ||
| + | Die rechte Darstellung $\rm (B)$ ist äquivalent zu $\rm (A)$: | ||
| + | *Mit der imaginären Funktion $z(t)$ erhält man: | ||
| + | :$$x_+(t) = x(t) + z(t).$$ | ||
| + | *Ein Vergleich beider Darstellungen zeigt, dass tatsächlich gilt: | ||
| + | :$$z(t) = {\rm j} \cdot y(t).$$}} | ||
==Zeigerdiagrammdarstellung der harmonischen Schwingung== | ==Zeigerdiagrammdarstellung der harmonischen Schwingung== | ||
| + | <br> | ||
| + | Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_{\rm T}t - \varphi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen | ||
| + | * $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$, | ||
| + | * $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$. | ||
| − | |||
| − | |||
| − | |||
| − | Somit lautet das Spektrum des analytischen Signals: | + | Somit lautet das Spektrum des analytischen Signals $($also ohne die Diracfunktion bei der Frequenz $f =-f_{\rm T})$: |
| − | $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm | + | :$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm |
T}) .$$ | T}) .$$ | ||
| − | Die dazugehörige Zeitfunktion erhält man durch Anwendung des Verschiebungssatzes: | + | Die dazugehörige Zeitfunktion erhält man durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]]: |
| − | $$x_+(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm T} t | + | :$$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t |
\hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | ||
| − | Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\ | + | Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger. |
| + | |||
| + | Im Folgenden bezeichnen wir den zeitlichen Verlauf eines analytischen und frequenzdikreten Signals $x_+(t)$ auch als $\text{Zeigerdiagramm}$. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ Aus Darstellungsgründen ist in der folgenden Grafik das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ nach links gedreht <br>(Realteil nach oben, Imaginärteil nach links). | ||
| + | |||
| + | [[Datei:P_ID712__Sig_T_4_2_S3.png|right|frame|Zeigerdiagramm einer harmonischen Schwingung]] | ||
Anhand dieser Grafik sind folgende Aussagen möglich: | Anhand dieser Grafik sind folgende Aussagen möglich: | ||
| − | *Zum Startzeitpunkt $t | + | *Zum Startzeitpunkt $t = 0$ liegt der Zeiger der Länge $A$ (Amplitude) mit dem Winkel $-\varphi$ in der komplexen Ebene. Im gezeichneten Beispiel gilt $\varphi = 45^\circ$. |
| − | *Für Zeiten $t | + | *Für Zeiten $t > 0$ dreht der Zeiger mit konstanter Winkelgeschwindigkeit (Kreisfrequenz) $\omega_{\rm T}$ in mathematisch positiver Richtung, das heißt entgegen dem Uhrzeigersinn. |
| − | *Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer. | + | *Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer der harmonischen Schwingung $x(t)$. |
| − | *Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte | + | *Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte von $x(t)$.}} |
==Zeigerdiagramm einer Summe harmonischer Schwingungen== | ==Zeigerdiagramm einer Summe harmonischer Schwingungen== | ||
| + | <br> | ||
| + | Für die weitere Beschreibung gehen wir für das analytische Signal von folgendem diskretem Spektrum aus: | ||
| − | + | [[Datei:P_ID715__Sig_T_4_2_S4.png|right|frame|Zeigerdiagramm eines Verbundes aus drei harmonischen Schwingungen]] | |
| − | $$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j} | + | :$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} |
\varphi_i}\cdot\delta (f - f_{i}) .$$ | \varphi_i}\cdot\delta (f - f_{i}) .$$ | ||
| − | Das linke Bild zeigt ein solches Spektrum für das Beispiel $I | + | Das linke Bild zeigt ein solches Spektrum für das Beispiel $I = 3$. Wählt man $I$ relativ groß und den Abstand zwischen benachbarten Spektrallinien entsprechend klein, so können mit obiger Gleichung auch (frequenz–) kontinuierliche Spektralfunktionen $X_+(f)$ angenähert werden. |
Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein: | Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein: | ||
| − | $$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{{\rm j}(\omega_i | + | :$$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i |
| − | \cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$ | + | \hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$ |
| − | Zu dieser Grafik | + | Zu dieser Grafik anzumerken: |
| − | *Die Skizze zeigt die Ausgangslage der Zeiger zum Startzeitpunkt $t | + | *Die Skizze zeigt die Ausgangslage der Zeiger zum Startzeitpunkt $t = 0$ entsprechend den Amplituden $A_i$ und den Phasenlagen $\varphi_i$. |
| − | *Die Spitze des resultierenden Zeigerverbundes ist durch das violette Kreuz markiert. Man erhält durch vektorielle Addition der drei Einzelzeiger für den Zeitpunkt $t | + | *Die Spitze des resultierenden Zeigerverbundes ist durch das violette Kreuz markiert. Man erhält durch vektorielle Addition der drei Einzelzeiger für den Zeitpunkt $t = 0$: |
| − | $$x_+(t) = 1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ)+ 2 +1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$ | + | :$$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$ |
| − | *Für Zeiten $t | + | *Für Zeiten $t > 0$ drehen die drei Zeiger mit unterschiedlichen Winkelgeschwindigkeiten $\omega_i = 2\pi f_i$. Der rote Zeiger dreht schneller als der grüne, aber langsamer als der blaue Zeiger. |
| − | *Da alle Zeiger entgegen dem Uhrzeigersinn drehen, wird sich auch der resultierende Zeiger $x_+(t)$ tendenziell in diese Richtung bewegen. Zum Zeitpunkt $t | + | *Da alle Zeiger entgegen dem Uhrzeigersinn drehen, wird sich auch der resultierende Zeiger $x_+(t)$ tendenziell in diese Richtung bewegen. Zum Zeitpunkt $t = 1\,µ\text {s}$ liegt die Spitze des resultierenen Zeigers für die gegebenen Parameterwerte bei |
| − | $$ \begin{align*} x_+(t = 1 {\rm \hspace{0.05cm} | + | :$$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm |
j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm | j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm | ||
j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 | j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 | ||
| Zeile 141: | Zeile 168: | ||
\hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm | \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm | ||
j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 | j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 | ||
| − | \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} \\ | + | \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} = \\ |
& = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot | & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot | ||
\hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm | \hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm | ||
| Zeile 147: | Zeile 174: | ||
e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx | e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx | ||
1.673- {\rm j} \cdot 0.464.\end{align*}$$ | 1.673- {\rm j} \cdot 0.464.\end{align*}$$ | ||
| − | *Die resultierende Zeigerspitze liegt nun aber nicht wie bei einer einzigen | + | *Die resultierende Zeigerspitze liegt nun aber nicht wie bei einer einzigen Schwingung auf einem Kreis, sondern es entsteht eine komplizierte geometrische Figur. |
| − | Das | + | |
| − | Zeigerdiagramm | + | |
| + | Das interaktive Applet [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physikalisches Signal & Analytisches Signal]] verdeutlicht $x_+(t)$ für die Summe dreier harmonischer Schwingungen. | ||
| + | |||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:Aufgabe_4.3:_Zeigerdiagrammdarstellung|Aufgabe 4.3: Zeigerdiagrammdarstellung]] | ||
| + | |||
| + | [[Aufgaben:Aufgabe_4.3Z:_Hilbert-Transformator|Aufgabe 4.3Z: Hilbert-Transformator]] | ||
| + | |||
| + | [[Aufgaben:Aufgabe_4.4:_Zeigerdiagramm_bei_ZSB-AM|Aufgabe 4.4: Zeigerdiagramm bei ZSB-AM]] | ||
| + | |||
| + | [[Aufgaben:Aufgabe_4.4Z:_Zeigerdiagramm_bei_ESB-AM|Aufgabe 4.4Z: Zeigerdiagramm bei ESB-AM]] | ||
| + | |||
| + | |||
| + | |||
| − | |||
Aktuelle Version vom 6. Mai 2021, 11:53 Uhr
Inhaltsverzeichnis
Definition im Frequenzbereich
Wir betrachten ein reelles bandpassartiges Signal $x(t)$ mit dem dazugehörigen Bandpass–Spektrum $X(f)$, das bezüglich des Frequenznullpunktes einen geraden Real– und einen ungeraden Imaginärteil besitzt. Es wird vorausgesetzt, dass die Trägerfrequenz $f_{\rm T}$ sehr viel größer als die Bandbreite des Bandpass–Signals $x(t)$ ist.
$\text{Definition:}$ Das zum physikalischen Signal $x(t)$ gehörige $\text{analytische Signal}$ $x_+(t)$ ist diejenige Zeitfunktion, deren Spektrum folgende Eigenschaft erfüllt:
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm f\ddot{u}r\hspace{0.2cm} {\it f} < 0.} }\right.$$
Die so genannte $\text{Signumfunktion}$ ist dabei für positive Frequenzwerte gleich $+1$ und für negative $f$–Werte gleich $-1$.
- Der (beidseitige) Grenzwert liefert $\sign(0) = 0$.
- Der Index „+” soll deutlich machen, dass $X_+(f)$ nur Anteile bei positiven Frequenzen besitzt.
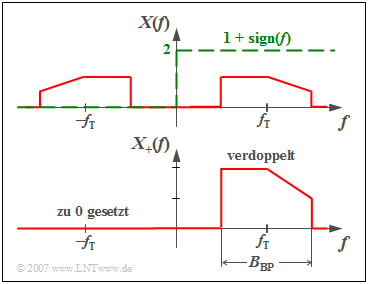
Aus der Grafik erkennt man die Berechnungsvorschrift für $X_+(f)$:
Das tatsächliche Bandpass–Spektrum $X(f)$ wird
- bei den positiven Frequenzen verdoppelt, und
- bei den negativen Frequenzen zu Null gesetzt.
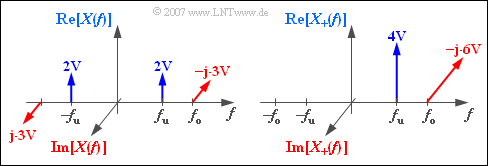
$\text{Beispiel 1:}$
Die Grafik zeigt
- links das diskrete und komplexe Spektrum $X(f)$ des Bandpass–Signals
- $$x(t) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t),$$
- rechts das (ebenfalls diskrete, komplexe) Spektrum des analytischen Signals $x_{+}(t)$.
Allgemeingültige Berechnungsvorschrift im Zeitbereich
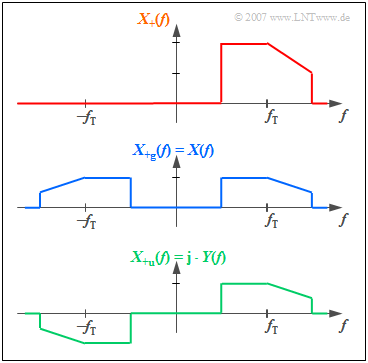
Wir betrachten nun das Spektrum $X_+(f)$ des analytischen Signals etwas genauer und teilen dieses in einen bezüglich $f = 0$ geraden Anteil $X_{\rm +g}(f)$ und einen ungeraden Anteil $X_{\rm +u}(f)$ auf:
- $$X_+(f) = X_{\rm +g}(f) + X_{\rm +u}(f).$$
Alle diese Spektren sind im allgemeinen komplex.
Berücksichtigt man den Zuordnungssatz der Fouriertransformation, so sind anhand der Grafik folgende Aussagen möglich:
- Der gerade Anteil $X_{\rm +g}(f)$ von $X_{+}(f)$ führt nach der Fouriertransformation zu einem reellen Zeitsignal, der ungerade Anteil $X_{\rm +u}(f)$ zu einem imaginären.
- Es ist offensichtlich, dass $X_{\rm +g}(f)$ gleich dem tatsächlichen Fourierspektrum $X(f)$ und damit der Realteil von $x_{\rm +g}(t)$ gleich dem vorgegebenen Signal $x(t)$ mit Bandpasseigenschaften ist.
- Bezeichnen wir den Imaginärteil mit $y(t)$, so lautet das analytische Signal:
- $$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$
- Nach den allgemein gültigen Gesetzen der Fouriertransformation entsprechend dem Zuordnungssatz gilt somit für die Spektralfunktion des Imaginärteils:
- $${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm sign}(f)}{ {\rm j}}\cdot X(f).$$
- Transformiert man diese Gleichung in den Zeitbereich, so wird aus der Multiplikation die Faltungsoperation, und man erhält:
- $$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star \hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau}}\hspace{0.15cm} {\rm d}\tau.$$
Darstellung mit der Hilberttransformation
An dieser Stelle ist es erforderlich, kurz auf eine weitere Spektraltransformation einzugehen, die im Buch Lineare zeitinvariante Systeme genauer behandelt wird.
$\text{Definition:}$ Für die $\text{Hilberttransformierte}$ $ {\rm H}\left\{x(t)\right\}$ einer Zeitfunktion $x(t)$ gilt:
- $$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$
- Dieses bestimmte Integral ist nicht auf einfache, herkömmliche Art lösbar, sondern muss mit Hilfe des Cauchy–Hauptwertsatzes ausgewertet werden.
- Entsprechend gilt im Frequenzbereich:
- $$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$
Das Ergebnis der letzten Seite lässt sich mit dieser Definition wie folgt zusammenfassen:
- Man erhält aus dem realen, physikalischen Bandpass–Signal $x(t)$ das analytische Signal $x_+(t)$, indem man zu $x(t)$ einen Imaginärteil entsprechend der Hilberttransformierten hinzufügt:
- $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- Die Hilberttransformierte $\text{H}\{x(t)\}$ verschwindet nur für den Fall $x(t) = \rm const.$ ⇒ Gleichsignal. Bei allen anderen Signalformen ist das analytische Signal $x_+(t)$ somit stets komplex.
- Aus dem analytischen Signal $x_+(t)$ kann das physikalisch Bandpass–Signal in einfacher Weise durch Realteilbildung ermittelt werden:
- $$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$
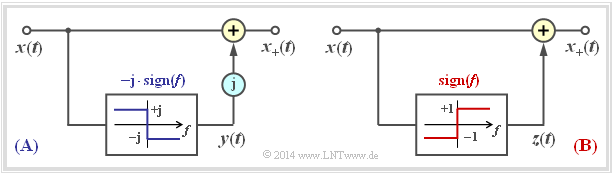
$\text{Beispiel 2:}$ Das Prinzip der Hilbert–Transformation wird durch die folgende Grafik nochmals verdeutlicht:
- Nach der linken Darstellung $\rm (A)$ kommt man vom physikalischen Signal $x(t)$ zum analytischen Signal $x_+(t)$, indem man einen Imaginärteil ${\rm j} \cdot y(t)$ hinzufügt.
- $y(t) = {\rm H}\left\{x(t)\right\}$ ist eine reelle Funktion, die sich am einfachsten im Spektralbereich durch Multiplikation des Spektrums $X(f)$ mit $- {\rm j} \cdot \sign(f)$ angeben lässt.
Die rechte Darstellung $\rm (B)$ ist äquivalent zu $\rm (A)$:
- Mit der imaginären Funktion $z(t)$ erhält man:
- $$x_+(t) = x(t) + z(t).$$
- Ein Vergleich beider Darstellungen zeigt, dass tatsächlich gilt:
- $$z(t) = {\rm j} \cdot y(t).$$
Zeigerdiagrammdarstellung der harmonischen Schwingung
Die Spektralfunktion $X(f)$ einer harmonischen Schwingung $x(t) = A \cdot \text{cos}(2\pi f_{\rm T}t - \varphi)$ besteht bekanntlich aus zwei Diracfunktionen bei den Frequenzen
- $+f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,
- $-f_{\rm T}$ mit dem komplexen Gewicht $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.
Somit lautet das Spektrum des analytischen Signals $($also ohne die Diracfunktion bei der Frequenz $f =-f_{\rm T})$:
- $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$
Die dazugehörige Zeitfunktion erhält man durch Anwendung des Verschiebungssatzes:
- $$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
Diese Gleichung beschreibt einen mit konstanter Winkelgeschwindigkeit $\omega_{\rm T} = 2\pi f_{\rm T}$ drehenden Zeiger.
Im Folgenden bezeichnen wir den zeitlichen Verlauf eines analytischen und frequenzdikreten Signals $x_+(t)$ auch als $\text{Zeigerdiagramm}$.
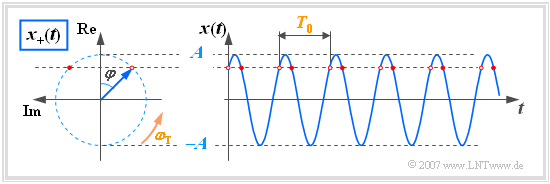
$\text{Beispiel 3:}$ Aus Darstellungsgründen ist in der folgenden Grafik das Koordinatensystem entgegen der üblichen Darstellung um $90^\circ$ nach links gedreht
(Realteil nach oben, Imaginärteil nach links).
Anhand dieser Grafik sind folgende Aussagen möglich:
- Zum Startzeitpunkt $t = 0$ liegt der Zeiger der Länge $A$ (Amplitude) mit dem Winkel $-\varphi$ in der komplexen Ebene. Im gezeichneten Beispiel gilt $\varphi = 45^\circ$.
- Für Zeiten $t > 0$ dreht der Zeiger mit konstanter Winkelgeschwindigkeit (Kreisfrequenz) $\omega_{\rm T}$ in mathematisch positiver Richtung, das heißt entgegen dem Uhrzeigersinn.
- Die Spitze des Zeigers liegt somit stets auf einem Kreis mit Radius $A$ und benötigt für eine Umdrehung genau die Zeit $T_0$, also die Periodendauer der harmonischen Schwingung $x(t)$.
- Die Projektion des analytischen Signals $x_+(t)$ auf die reelle Achse, durch rote Punkte markiert, liefert die Augenblickswerte von $x(t)$.
Zeigerdiagramm einer Summe harmonischer Schwingungen
Für die weitere Beschreibung gehen wir für das analytische Signal von folgendem diskretem Spektrum aus:
- $$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} \varphi_i}\cdot\delta (f - f_{i}) .$$
Das linke Bild zeigt ein solches Spektrum für das Beispiel $I = 3$. Wählt man $I$ relativ groß und den Abstand zwischen benachbarten Spektrallinien entsprechend klein, so können mit obiger Gleichung auch (frequenz–) kontinuierliche Spektralfunktionen $X_+(f)$ angenähert werden.
Im rechten Bild ist die dazugehörige Zeitfunktion angedeutet. Diese lautet allgemein:
- $$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i \hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
Zu dieser Grafik anzumerken:
- Die Skizze zeigt die Ausgangslage der Zeiger zum Startzeitpunkt $t = 0$ entsprechend den Amplituden $A_i$ und den Phasenlagen $\varphi_i$.
- Die Spitze des resultierenden Zeigerverbundes ist durch das violette Kreuz markiert. Man erhält durch vektorielle Addition der drei Einzelzeiger für den Zeitpunkt $t = 0$:
- $$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$
- Für Zeiten $t > 0$ drehen die drei Zeiger mit unterschiedlichen Winkelgeschwindigkeiten $\omega_i = 2\pi f_i$. Der rote Zeiger dreht schneller als der grüne, aber langsamer als der blaue Zeiger.
- Da alle Zeiger entgegen dem Uhrzeigersinn drehen, wird sich auch der resultierende Zeiger $x_+(t)$ tendenziell in diese Richtung bewegen. Zum Zeitpunkt $t = 1\,µ\text {s}$ liegt die Spitze des resultierenen Zeigers für die gegebenen Parameterwerte bei
- $$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}50 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} = \\ & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}18^\circ}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx 1.673- {\rm j} \cdot 0.464.\end{align*}$$
- Die resultierende Zeigerspitze liegt nun aber nicht wie bei einer einzigen Schwingung auf einem Kreis, sondern es entsteht eine komplizierte geometrische Figur.
Das interaktive Applet Physikalisches Signal & Analytisches Signal verdeutlicht $x_+(t)$ für die Summe dreier harmonischer Schwingungen.
Aufgaben zum Kapitel
Aufgabe 4.3: Zeigerdiagrammdarstellung
Aufgabe 4.3Z: Hilbert-Transformator
Aufgabe 4.4: Zeigerdiagramm bei ZSB-AM
Aufgabe 4.4Z: Zeigerdiagramm bei ESB-AM