Kanalcodierung/Informationstheoretische Grenzen der Kanalcodierung: Unterschied zwischen den Versionen
Wael (Diskussion | Beiträge) |
|||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== Kanalcodierungstheorem und Kanalkapazität == | == Kanalcodierungstheorem und Kanalkapazität == | ||
<br> | <br> | ||
| − | Wir betrachten weiterhin einen binären Blockcode mit $k$ Informationsbits pro Block und Codeworte der Länge $n$, woraus sich die Coderate $R=k/n$ mit der Einheit „Informationsbit/Codesymbol” ergibt.<br> | + | Wir betrachten weiterhin einen binären Blockcode mit $k$ Informationsbits pro Block und Codeworte der Länge $n$, woraus sich die Coderate $R=k/n$ mit der Einheit „Informationsbit/Codesymbol” ergibt.<br> |
| − | Der geniale Informationstheoretiker [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] hat sich schon 1948 sehr intensiv mit der Korrekturfähigkeit solcher Codes beschäftigt und hierfür für jeden Kanal eine Grenze angegeben, die sich allein aus informationstheoretischen Überlegungen ergibt. Bis heute wurde noch kein Code gefunden, der diese Grenze übersteigt, und dies wird auch so bleiben.<br> | + | Der geniale Informationstheoretiker [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] hat sich schon 1948 sehr intensiv mit der Korrekturfähigkeit solcher Codes beschäftigt und hierfür für jeden Kanal eine Grenze angegeben, die sich allein aus informationstheoretischen Überlegungen ergibt. Bis heute wurde noch kein Code gefunden, der diese Grenze übersteigt, und dies wird auch so bleiben.<br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Shannons Kanalcodierungstheorem:}$ Zu jedem Kanal mit der Kanalkapazität $C > 0$ existiert stets (mindestens) ein Code, dessen Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R$ kleiner als die Kanalkapazität $C$ | + | $\text{Shannons Kanalcodierungstheorem:}$ Zu jedem Kanal mit der Kanalkapazität $C > 0$ existiert stets (mindestens) ein Code, dessen Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R$ kleiner ist als die Kanalkapazität $C$. Voraussetzung hierfür ist, dass für die Blocklänge dieses Codes gilt: $n \to \infty$.}}<br> |
| − | Die Umkehrung ist ebenfalls zutreffend und besagt:<br> | + | ''Anmerkungen:'' |
| + | *Die Aussage „Die Fehlerwahrscheinlichkeit geht gegen Null” ist nicht identisch mit der Aussage „Die Übertragung ist fehlerfrei”. Beispiel: Bei einer unendlich langen Folge werden endlich viele Symbole verfälscht. | ||
| + | *Bei manchen Kanälen geht auch mit $R=C$ die Fehlerwahrscheinlichkeit noch gegen Null (aber nicht bei allen). | ||
| + | |||
| + | |||
| + | Die Umkehrung des Kanalcodierungstheorems ist ebenfalls zutreffend und besagt:<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Umkehrschluss:}$ | + | $\text{Umkehrschluss:}$ Ist die Coderate $R$ größer als die Kanalkapazität $C$, so kann eine beliebig kleine Fehlerwahrscheinlichkeit auf keinen Fall erreicht werden.}}<br> |
| − | Zur Herleitung und Berechnung der Kanalkapazität gehen wir zunächst von einem digitalen Kanal mit $M_x$ möglichen Eingangswerten $x$ und $M_y$ möglichen Ausgangswerten $y$ aus. | + | Zur Herleitung und Berechnung der Kanalkapazität gehen wir zunächst von einem digitalen Kanal mit $M_x$ möglichen Eingangswerten $x$ und $M_y$ möglichen Ausgangswerten $y$ aus. Dann gilt für den mittleren Transinformationsgehalt – kurz die [[Informationstheorie/Verschiedene_Entropien_zweidimensionaler_Zufallsgrößen#Transinformation_zwischen_zwei_Zufallsgr.C3.B6.C3.9Fen|Transinformation]] (englisch: <i>Mutual Information</i>) – zwischen der Zufallsgröße $x$ am Kanaleingang und der Zufallsgröße $y$ an seinem Ausgang: |
::<math>I(x; y) =\sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y} \hspace{0.15cm}{\rm Pr}(x_i, y_j) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{{\rm Pr}(y_j)} = \sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y}\hspace{0.15cm}{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i) \cdot {\rm Pr}(x_i) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{\sum_{k= 1}^{M_X} {\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_k) \cdot {\rm Pr}(x_k)} | ::<math>I(x; y) =\sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y} \hspace{0.15cm}{\rm Pr}(x_i, y_j) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{{\rm Pr}(y_j)} = \sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y}\hspace{0.15cm}{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i) \cdot {\rm Pr}(x_i) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{\sum_{k= 1}^{M_X} {\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_k) \cdot {\rm Pr}(x_k)} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Beim Übergang von der ersten zur zweiten Gleichung wurden dabei der [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit#Bedingte_Wahrscheinlichkeit_.281.29| Satz von Bayes]] sowie der [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit#R.C3.BCckschlusswahrscheinlichkeit| Satz von der totalen Wahrscheinlichkeit]] berücksichtigt. Weiter ist anzumerken: | + | Beim Übergang von der ersten zur zweiten Gleichung wurden dabei der [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit#Bedingte_Wahrscheinlichkeit_.281.29| Satz von Bayes]] sowie der [[Stochastische_Signaltheorie/Statistische_Abh%C3%A4ngigkeit_und_Unabh%C3%A4ngigkeit#R.C3.BCckschlusswahrscheinlichkeit| Satz von der totalen Wahrscheinlichkeit]] berücksichtigt. |
| − | *Der <i>Logarithmus dualis</i> ist hier mit „log<sub>2</sub>” bezeichnet ist. Teilweise verwenden wir | + | |
| − | *Im Gegensatz zum Buch [[Informationstheorie]] unterscheiden wir im Folgenden nicht zwischen der Zufallsgröße (Großbuchstaben | + | Weiter ist anzumerken: |
| + | *Der <i>Logarithmus dualis</i> ist hier mit „log<sub>2</sub>” bezeichnet ist. Teilweise verwenden wir in unserem Lerntutorial hierfür auch „ld”. | ||
| + | *Im Gegensatz zum Buch [[Informationstheorie]] unterscheiden wir im Folgenden nicht zwischen der Zufallsgröße $($Großbuchstaben $X$ bzw. $Y)$ und den Realisierungen $($Kleinbuchstaben $x$ bzw. $y)$.<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die von Shannon eingeführte '''Kanalkapazität''' gibt die maximale Transinformation $I(x; y)$ zwischen der Eingangsgröße $x$ und der Ausgangsgröße $y$ an: | + | $\text{Definition:}$ Die von Shannon eingeführte '''Kanalkapazität''' gibt die maximale Transinformation $I(x; y)$ zwischen der Eingangsgröße $x$ und der Ausgangsgröße $y$ an: |
::<math>C = \max_{{{\rm Pr}(x_i)}} \hspace{0.1cm} I(X; Y) \hspace{0.05cm}.</math> | ::<math>C = \max_{{{\rm Pr}(x_i)}} \hspace{0.1cm} I(X; Y) \hspace{0.05cm}.</math> | ||
| Zeile 37: | Zeile 44: | ||
Hinzugefügt werden muss die Pseudo–Einheit „bit/Kanalzugriff”.}}<br> | Hinzugefügt werden muss die Pseudo–Einheit „bit/Kanalzugriff”.}}<br> | ||
| − | Da die Maximierung der Transinformation über alle möglichen (diskreten) Eingangsverteilungen ${\rm Pr}(x_i)$ erfolgen muss, ist die Kanalkapazität unabhängig vom Eingang und damit eine reine Kanalkenngröße.<br> | + | Da die Maximierung der Transinformation über alle möglichen (diskreten) Eingangsverteilungen ${\rm Pr}(x_i)$ erfolgen muss, ist die Kanalkapazität unabhängig vom Eingang und damit eine reine Kanalkenngröße.<br> |
== Kanalkapazität des BSC–Modells == | == Kanalkapazität des BSC–Modells == | ||
<br> | <br> | ||
| − | + | Wir wenden nun diese Definitionen auf das [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Symmetric_Channel_.E2.80.93_BSC|BSC–Modell]] (''Binary Symmetric Channel '') an: | |
| − | ::<math>I(x; y) = {\rm Pr}(y = 0 \hspace{0. | + | ::<math>I(x; y) = {\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) |
| − | \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 0 \hspace{0. | + | \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 0)} |
| − | + {\rm Pr}(y = 1 \hspace{0. | + | + {\rm Pr}(y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) |
| − | \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 1 \hspace{0. | + | \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 1)} |
+ </math> | + </math> | ||
::<math>\hspace{1.45cm} + \hspace{0.15cm}{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) | ::<math>\hspace{1.45cm} + \hspace{0.15cm}{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) | ||
| Zeile 69: | Zeile 76: | ||
*Wir berücksichtigen zudem die BSC–Übergangswahrscheinlichkeiten: | *Wir berücksichtigen zudem die BSC–Übergangswahrscheinlichkeiten: | ||
| − | ::<math>{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 0) | + | ::<math>{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = \varepsilon \hspace{0.05cm},</math> |
| − | ::<math>{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 0) | + | ::<math>{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = 1-\varepsilon \hspace{0.05cm}.</math> |
*Nach Zusammenfassen je zweier Terme erhält man somit: | *Nach Zusammenfassen je zweier Terme erhält man somit: | ||
| Zeile 76: | Zeile 83: | ||
::<math>C \hspace{0.15cm} = \hspace{0.15cm} 2 \cdot 1/2 \cdot \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{\varepsilon}{1/2 }+ | ::<math>C \hspace{0.15cm} = \hspace{0.15cm} 2 \cdot 1/2 \cdot \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{\varepsilon}{1/2 }+ | ||
2 \cdot 1/2 \cdot (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1- \varepsilon}{1/2 } | 2 \cdot 1/2 \cdot (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1- \varepsilon}{1/2 } | ||
| − | \varepsilon \cdot {\rm ld } \hspace{0.15cm}2 - \varepsilon \cdot {\rm log_2 } \hspace{0.15cm} \frac{1}{\varepsilon }+ (1- \varepsilon) \cdot {\rm | + | \varepsilon \cdot {\rm ld } \hspace{0.15cm}2 - \varepsilon \cdot {\rm log_2 } \hspace{0.15cm} \frac{1}{\varepsilon }+ (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm} 2 - (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}</math> |
| + | ::<math>\Rightarrow \hspace{0.3cm} C \hspace{0.15cm} = \hspace{0.15cm} 1 - H_{\rm bin}(\varepsilon). </math> | ||
*Verwendet ist hier die ''binäre Entropiefunktion'': | *Verwendet ist hier die ''binäre Entropiefunktion'': | ||
| Zeile 83: | Zeile 91: | ||
(1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\hspace{0.05cm}.</math> | (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\hspace{0.05cm}.</math> | ||
| + | Die folgende rechte Grafik zeigt die BSC–Kanalkapazität abhängig von der Verfälschungswahrscheinlichkeit $\varepsilon$. Links ist zum Vergleich die binäre Entropiefunktion dargestellt, die bereits im Kapitel [[Informationstheorie/Ged%C3%A4chtnislose_Nachrichtenquellen#Bin.C3.A4re_Entropiefunktion|Gedächtnislose Nachrichtenquellen]] des Buches „Informationstheorie” definiert wurde.<br> | ||
| − | + | [[Datei:P ID2379 KC T 1 7 S2 v2.png|rght|frame|Kanalkapazität des BSC–Modells|class=fit]] | |
| − | |||
| − | [[Datei:P ID2379 KC T 1 7 S2 v2.png| | ||
| − | |||
Man erkennt aus dieser Darstellung: | Man erkennt aus dieser Darstellung: | ||
| − | *Die Verfälschungswahrscheinlichkeit $\varepsilon$ führt zur Kanalkapazität $C(\varepsilon)$. Eine fehlerfreie Decodierung nach bestmöglicher Codierung ist nach dem [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t |Kanalcodierungstheorem]] nur dann möglich, wenn die Coderate $R$ | + | *Die Verfälschungswahrscheinlichkeit $\varepsilon$ führt zur Kanalkapazität $C(\varepsilon)$. Eine fehlerfreie Decodierung nach bestmöglicher Codierung ist nach dem [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t |Kanalcodierungstheorem]] nur dann möglich, wenn die Coderate $R$ nicht größer ist als $C(\varepsilon)$. |
| − | *Mit $\varepsilon = 10\%$ ist wegen $C(0.1) = 0.531$ eine fehlerfreie Decodierung nicht möglich, wenn die Coderate $R | + | *Mit $\varepsilon = 10\%$ ist wegen $C(0.1) = 0.531$ eine fehlerfreie Decodierung nicht möglich, wenn die Coderate $R > 0.531$ beträgt. Bei 50–prozentiger Verfälschung ist eine fehlerfreie Decodierung auch bei beliebig kleiner Coderate unmöglich: $C(0.5) = 0$ .<br> |
| − | *Aus informationstheoretischer Sicht ist $\varepsilon = 1$ (Invertierung aller Bits) gleich gut wie $\varepsilon = 0$ (fehlerfreie Übertragung). Ebenso ist $\varepsilon = 0.9$ äquivalent zu $\varepsilon = 0.1$. Eine fehlerfreie Decodierung erzielt man hier durch Vertauschen der Nullen und Einsen, also durch ein so genanntes <i>Mapping</i>.<br> | + | *Aus informationstheoretischer Sicht ist $\varepsilon = 1$ (Invertierung aller Bits) gleich gut wie $\varepsilon = 0$ (fehlerfreie Übertragung). Ebenso ist $\varepsilon = 0.9$ äquivalent zu $\varepsilon = 0.1$. Eine fehlerfreie Decodierung erzielt man hier durch Vertauschen der Nullen und Einsen, also durch ein so genanntes <i>Mapping</i>.<br> |
== Kanalkapazität des AWGN–Modells== | == Kanalkapazität des AWGN–Modells== | ||
<br> | <br> | ||
| − | [[Datei:P ID2372 KC T 1 7 S3a.png|right|frame| | + | [[Datei:P ID2372 KC T 1 7 S3a.png|right|frame|AWGN–Kanalmodell|class=fit]] |
| − | Wir betrachten nun den [[Digitalsignalübertragung/Systemkomponenten_eines_Basisbandübertragungssystems#.C3.9Cbertragungskanal_und_St.C3.B6rungen|AWGN–Kanal]] (<i>Additive White Gaussian Noise</i>). Hier gilt für das Ausgangssignal $y = x + n$, wobei $n$ eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|gaußverteilte Zufallsgröße]] beschreibt, und es gilt für deren Erwartungswerte (Momente): | + | Wir betrachten nun den [[Digitalsignalübertragung/Systemkomponenten_eines_Basisbandübertragungssystems#.C3.9Cbertragungskanal_und_St.C3.B6rungen|AWGN–Kanal]] (<i>Additive White Gaussian Noise</i> ). Hier gilt für das Ausgangssignal $y = x + n$, wobei $n$ eine [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|gaußverteilte Zufallsgröße]] beschreibt, und es gilt für deren Erwartungswerte (Momente): |
| − | :$${\rm E}[n] = 0, | + | :$${\rm E}[n] = 0,\hspace{1cm} {\rm E}[n^2] = P_n.$$ |
| − | |||
| − | Damit ergibt sich unabhängig vom Eingangssignal $x$ (analog oder digital) stets ein | + | Damit ergibt sich unabhängig vom Eingangssignal $x$ (analog oder digital) stets ein wertkontinuierliches Ausgangssignal $y$, und in der [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t|Gleichung für die Transinformation]] ist $M_y \to\infty$ einzusetzen.<br> |
| − | Die Berechnung der Kanalkapazität für den AWGN–Kanal wird hier nur in Stichworten angegeben. Die genaue Herleitung finden Sie im vierten Hauptkapitel „Wertdiskrete Informationstheorie” des Buches [[Informationstheorie]] | + | Die Berechnung der Kanalkapazität für den AWGN–Kanal wird hier nur in Stichworten angegeben. Die genaue Herleitung finden Sie im vierten Hauptkapitel „Wertdiskrete Informationstheorie” des Buches [[Informationstheorie]]. |
| − | *Die im Hinblick auf maximale Transinformation optimierte Eingangsgröße $x$ wird mit Sicherheit wertkontinuierlich sein, das heißt, beim AWGN–Kanal gilt außer $M_y \to\infty$ auch $M_x \to\infty$. | + | *Die im Hinblick auf maximale Transinformation optimierte Eingangsgröße $x$ wird mit Sicherheit wertkontinuierlich sein, das heißt, beim AWGN–Kanal gilt außer $M_y \to\infty$ auch $M_x \to\infty$. |
| − | *Während bei wertdiskretem Eingang über alle ${\rm Pr}(x_i)$ zu optimieren ist, erfolgt nun die Optimierung anhand der [[Stochastische_Signaltheorie/Gau%C3%9Fverteilte_Zufallsgr%C3%B6%C3%9Fe#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion| WDF]] $f_x(x)$ des Eingangssignals unter der Nebenbedingung [[Digitalsignal%C3%BCbertragung/Optimierung_der_Basisband%C3%BCbertragungssysteme#Leistungs.E2.80. | + | *Während bei wertdiskretem Eingang über alle ${\rm Pr}(x_i)$ zu optimieren ist, erfolgt nun die Optimierung anhand der [[Stochastische_Signaltheorie/Gau%C3%9Fverteilte_Zufallsgr%C3%B6%C3%9Fe#Wahrscheinlichkeitsdichte-_und_Verteilungsfunktion| WDF]] $f_x(x)$ des Eingangssignals unter der Nebenbedingung [[Digitalsignal%C3%BCbertragung/Optimierung_der_Basisband%C3%BCbertragungssysteme#Leistungs.E2.80.93_und_Spitzenwertbegrenzung| Leistungsbegrenzung]]: |
| − | ::<math>C = \max_{f_x(x)} \hspace{0.1cm} I(x; y)\hspace{0.05cm},\hspace{0.3cm}{\rm wobei \hspace{0.15cm} gelten \hspace{0.15cm} muss:}\hspace{0.15cm} {\rm E} \left [ x^2 \right ] \le P_x \hspace{0.05cm}.</math> | + | ::<math>C = \max_{f_x(x)} \hspace{0.1cm} I(x; y)\hspace{0.05cm},\hspace{0.3cm}{\rm wobei \hspace{0.15cm} gelten \hspace{0.15cm} muss} \text{:}\hspace{0.15cm} {\rm E} \left [ x^2 \right ] \le P_x \hspace{0.05cm}.</math> |
| − | *Die Optimierung liefert für die Eingangs–WDF ebenfalls eine Gaußverteilung ⇒ $x$, $n$ und $y$ sind gaußverteilt gemäß den Dichtefunktionen $f_x(x)$, $f_n(n)$ und $f_y(y)$ | + | *Die Optimierung liefert für die Eingangs–WDF ebenfalls eine Gaußverteilung ⇒ $x$, $n$ und $y$ sind gaußverteilt gemäß den Dichtefunktionen $f_x(x)$, $f_n(n)$ und $f_y(y)$. Die entsprechenden Leistungen benennen wir $P_x$, $P_n$ und $P_y$.<br> |
| − | *Nach längerer Rechnung erhält man für die Kanalkapazität unter Verwendung des <i>Logarithmus dualis</i> $\log_2(\cdot)$ – wiederum mit der Pseudo–Einheit „bit/Kanalzugriff”: | + | *Nach längerer Rechnung erhält man für die Kanalkapazität unter Verwendung des <i>Logarithmus dualis</i> $\log_2(\cdot)$ – wiederum mit der Pseudo–Einheit „bit/Kanalzugriff”: |
| − | ::<math>C = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_y}{P_n }} = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_x + P_n}{P_n }} = | + | ::<math>C = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_y}{P_n }} = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_x + P_n}{P_n }} = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + \frac{P_x}{P_n } \right )\hspace{0.05cm}.</math> |
| − | *Beschreibt $x$ ein zeitdiskretes Signal mit der Symbolrate $1/T_{\rm S}$, so muss dieses auf $B = 1/(2T_{\rm S})$ bandbegrenzt sein, und die gleiche Bandbreite $B$ muss man für das Rauschsignal $n$ ansetzen ⇒ „Rauschbandbreite”: | + | *Beschreibt $x$ ein zeitdiskretes Signal mit der Symbolrate $1/T_{\rm S}$, so muss dieses auf $B = 1/(2T_{\rm S})$ bandbegrenzt sein, und die gleiche Bandbreite $B$ muss man auch für das Rauschsignal $n$ ansetzen ⇒ „Rauschbandbreite”: |
::<math>P_X = \frac{E_{\rm S}}{T_{\rm S} } \hspace{0.05cm}, \hspace{0.4cm} P_N = \frac{N_0}{2T_{\rm S} }\hspace{0.05cm}. </math> | ::<math>P_X = \frac{E_{\rm S}}{T_{\rm S} } \hspace{0.05cm}, \hspace{0.4cm} P_N = \frac{N_0}{2T_{\rm S} }\hspace{0.05cm}. </math> | ||
| − | *Somit lässt sich die AWGN–Kanalkapazität auch durch die '''Sendeenergie pro Symbol''' $(E_{\rm S})$ und die '''Rauschleistungsdichte''' $(N_0)$ ausdrücken: | + | *Somit lässt sich die AWGN–Kanalkapazität auch durch die '''Sendeenergie pro Symbol''' $(E_{\rm S})$ und die '''Rauschleistungsdichte''' $(N_0)$ ausdrücken: |
| − | ::<math>C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + | + | ::<math>C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{1.9cm} |
| − | { | + | \text {Einheit:}\hspace{0.3cm} \frac{\rm bit}{\rm Kanalzugriff}\hspace{0.05cm}.</math> |
| − | ::<math>C^{\star} = \frac{C}{T_{\rm S} } = B \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + | + | *Mit der folgenden Gleichung erhält man die Kanalkapazität pro Zeiteinheit (Kennzeichnung durch $^{\star})$: |
| − | { | + | ::<math>C^{\star} = \frac{C}{T_{\rm S} } = B \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{0.8cm} |
| + | \text {Einheit:} \hspace{0.3cm} \frac{\rm bit}{\rm Zeiteinheit}\hspace{0.05cm}.</math><br> | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | *Für $E_{\rm S}/N_0 = 7.5$ ⇒ $10 \cdot \lg \, E_{\rm S}/N_0 = 8.75 \, \rm dB$ erhält man die Kanalkapazität $C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm} (16) = 2 \, \rm bit/Kanalzugriff$. | + | *Für $E_{\rm S}/N_0 = 7.5$ ⇒ $10 \cdot \lg \, E_{\rm S}/N_0 = 8.75 \, \rm dB$ erhält man die Kanalkapazität $C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm} (16) = 2 \, \rm bit/Kanalzugriff$. |
| − | *Bei einem Kanal mit der (physikalischen) Bandbreite $B = 4 \, \rm kHz$, was der Abtastrate $f_{\rm A} = 8\, \rm kHz$ entspricht, gilt zudem $C^\star = 16 \, \rm kbit/s$.}}<br> | + | *Bei einem Kanal mit der (physikalischen) Bandbreite $B = 4 \, \rm kHz$, was der Abtastrate $f_{\rm A} = 8\, \rm kHz$ entspricht, gilt zudem $C^\star = 16 \, \rm kbit/s$.}}<br> |
| − | |||
| − | Ein Vergleich verschiedener Codierverfahren bei konstantem $E_{\rm S}$ (Energie ''pro übertragenem Symbol'') ist nicht fair. Vielmehr sollte man für diesen Vergleich die Energie $E_{\rm B}$ ''pro Nutzbit'' fest vorgeben. Dabei | + | Ein Vergleich verschiedener Codierverfahren bei konstantem $E_{\rm S}$ (Energie ''pro übertragenem Symbol'' ) ist allerdings nicht fair. Vielmehr sollte man für diesen Vergleich die Energie $E_{\rm B}$ ''pro Nutzbit'' fest vorgeben. Dabei gelten folgende Zusammenhänge: |
::<math>E_{\rm S} = R \cdot E_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ::<math>E_{\rm S} = R \cdot E_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| Zeile 140: | Zeile 145: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Kanalcodierungstheorem für den AWGN–Kanal:}$ |
| + | |||
| + | Eine fehlerfreie Decodierung $($bei unendlich langen Blöcken ⇒ $n \to \infty)$ ist immer dann möglich, falls die Coderate $R$ kleiner ist als die Kanalkapazität $C$: | ||
::<math>R < C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 +2 \cdot R\cdot E_{\rm B}/{N_0 } \right )\hspace{0.05cm}.</math> | ::<math>R < C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 +2 \cdot R\cdot E_{\rm B}/{N_0 } \right )\hspace{0.05cm}.</math> | ||
| − | Für jede Coderate $R$ lässt sich damit das erforderliche $E_{\rm B}/N_0$ des AWGN–Kanals ermitteln, damit eine fehlerfreie Decodierung möglich ist. Man erhält für den Grenzfall $R = C$: | + | Für jede Coderate  $R$ lässt sich damit das erforderliche $E_{\rm B}/N_0$ des AWGN–Kanals ermitteln, damit eine fehlerfreie Decodierung gerade noch möglich ist. Man erhält für den Grenzfall $R = C$: |
::<math>{E_{\rm B} }/{N_0} > \frac{2^{2R}-1}{2R } \hspace{0.05cm}.</math>}} | ::<math>{E_{\rm B} }/{N_0} > \frac{2^{2R}-1}{2R } \hspace{0.05cm}.</math>}} | ||
| − | Die Grafik fasst das Ergebnis zusammen, wobei die Ordinate $R$ im linearen Maßstab und die Abszisse $E_{\rm B}/{N_0 }$ logarithmisch aufgetragen ist. | + | Die Grafik fasst das Ergebnis zusammen, wobei die Ordinate $R$ im linearen Maßstab und die Abszisse $E_{\rm B}/{N_0 }$ logarithmisch aufgetragen ist. |
| + | [[Datei:P ID2373 KC T 1 7 S3b v3.png|right|frame|Kanalkapazität des AWGN–Kanals|class=fit]] | ||
*Außerhalb der blauen Fläche ist eine fehlerfreie Codierung nicht möglich. | *Außerhalb der blauen Fläche ist eine fehlerfreie Codierung nicht möglich. | ||
| − | *Die blaue Grenzkurve gibt die Kanalkapazität $C$ des AWGN–Kanals an.<br> | + | *Die blaue Grenzkurve gibt die Kanalkapazität $C$ des AWGN–Kanals an.<br> |
| − | + | <br clear=all> | |
| − | |||
| − | |||
Aus dieser Grafik und obiger Gleichung lässt sich Folgendes ableiten: | Aus dieser Grafik und obiger Gleichung lässt sich Folgendes ableiten: | ||
| − | *Die Kanalkapazität $C$ steigt etwas weniger als linear mit $10 \cdot \lg \, E_{\rm B}/N_0 $ an. In der Grafik sind einige ausgewählte Funktionswerte als blaue Kreuze angegeben.<br> | + | *Die Kanalkapazität $C$ steigt etwas weniger als linear mit $10 \cdot \lg \, E_{\rm B}/N_0 $ an. In der Grafik sind einige ausgewählte Funktionswerte als blaue Kreuze angegeben.<br> |
| − | *Ist $10 \cdot \lg \, E_{\rm B}/N_0 < -1.59 \, \rm dB$, so ist eine fehlerfreie Decodierung prinzipiell unmöglich. Beträgt die Coderate $R = 0.5$, so muss $10 \cdot \lg \, E_{\rm B}/N_0 > 0 \, \rm dB$ sein ⇒ $E_{\rm B} > N_0$.<br> | + | *Ist $10 \cdot \lg \, E_{\rm B}/N_0 < -1.59 \, \rm dB$, so ist eine fehlerfreie Decodierung prinzipiell unmöglich. Beträgt die Coderate $R = 0.5$, so muss $10 \cdot \lg \, E_{\rm B}/N_0 > 0 \, \rm dB$ sein ⇒ $E_{\rm B} > N_0$.<br> |
| − | *Für alle binären Codes gilt per se $0 | + | *Für alle binären Codes gilt per se $0 < R ≤ 1$. Nur mit <i>nichtbinären</i> Codes sind Coderaten $R > 1$ möglich. Beispielsweise beträgt die maximal mögliche Coderate eines quaternären Codes $R = \log_2 \, M_y = \log_2 \, 4 = 2$.<br> |
| − | *Alle eindimensionalen Modulationsarten – also solche Verfahren, die nur die Inphase– oder nur die Quadraturkomponente nutzen wie [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|2–ASK]], [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#Binary_Phase_Shift_Keying_.28BPSK.29|BPSK]] und [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_bin.C3.A4rer_FSK_.282.E2.80.93FSK.29|2–FSK]] – müssen im blauen Bereich liegen.<br> | + | *Alle eindimensionalen Modulationsarten – also solche Verfahren, die nur die Inphase– oder nur die Quadraturkomponente nutzen wie [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#On.E2.80.93Off.E2.80.93Keying_.282.E2.80.93ASK.29|2–ASK]], [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_kohärenter_Demodulation#Binary_Phase_Shift_Keying_.28BPSK.29|BPSK]] und [[Digitalsignalübertragung/Trägerfrequenzsysteme_mit_nichtkohärenter_Demodulation#Nichtkoh.C3.A4rente_Demodulation_von_bin.C3.A4rer_FSK_.282.E2.80.93FSK.29|2–FSK]] – müssen im blauen Bereich der vorliegenden Grafik liegen.<br> |
| + | *Wie im Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#Maximale_Coderate_f.C3.BCr_QAM.E2.80.93Strukturen|Maximale Coderate für QAM–Strukturen]] des Buches „Informationstheorie” gezeigt wird, gibt es für zweidimensionale Modulationsarten wie zum Beispiel die [[Modulationsverfahren/Quadratur–Amplitudenmodulation|Quadratur–Amplitudenmodulation]] eine „freundlichere” Grenzkurve. | ||
== AWGN–Kanalkapazität für binäre Eingangssignale == | == AWGN–Kanalkapazität für binäre Eingangssignale == | ||
<br> | <br> | ||
| − | In diesem Buch beschränken wir uns vorwiegend auf binäre Codes, also auf das Galoisfeld ${\rm GF}(2^n)$. Damit ist | + | In diesem Buch beschränken wir uns vorwiegend auf binäre Codes, also auf das Galoisfeld ${\rm GF}(2^n)$. Damit ist |
| − | [[Datei:P ID2374 KC T 1 7 S4a.png|right|frame|Bedingte | + | [[Datei:P ID2374 KC T 1 7 S4a.png|right|frame|Bedingte Dichtefunktionen bei AWGN–Kanal und binärem Eingang]] |
| − | *zum einen die Coderate auf den Bereich $R ≤ 1$ begrenzt,<br> | + | *zum einen die Coderate auf den Bereich $R ≤ 1$ begrenzt,<br> |
| − | *zum zweiten auch für $R ≤ 1$ nicht die gesamte blaue Region verfügbar (siehe vorherige Seite) . | + | *zum zweiten auch für $R ≤ 1$ nicht die gesamte blaue Region verfügbar (siehe vorherige Seite). |
| − | Die nun gültige Region ergibt sich aus der [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t|allgemeinen Gleichung]] der Transinformation durch | + | |
| − | *die Parameter $M_x = 2$ und $M_y \to \infty$,<br> | + | Die nun gültige Region ergibt sich aus der [[Kanalcodierung/Informationstheoretische_Grenzen_der_Kanalcodierung#Kanalcodierungstheorem_und_Kanalkapazit.C3.A4t|allgemeinen Gleichung]] der Transinformation durch |
| − | *bipolare Signalisierung ⇒ $x=0$ → $\tilde{x} = +1$ und $x=1$ → $\tilde{x} = -1$,<br> | + | *die Parameter $M_x = 2$ und $M_y \to \infty$,<br> |
| − | *den Übergang von bedingten Wahrscheinlichkeiten ${\rm Pr}(\tilde{x}_i)$ zu bedingten Wahrscheinlichkeitsdichtefunktionen,<br> | + | *bipolare Signalisierung ⇒ $x=0$ → $\tilde{x} = +1$ und $x=1$ → $\tilde{x} = -1$,<br> |
| + | *den Übergang von bedingten Wahrscheinlichkeiten ${\rm Pr}(\tilde{x}_i)$ zu bedingten Wahrscheinlichkeitsdichtefunktionen,<br> | ||
*Ersetzen der Summe durch eine Integration.<br><br> | *Ersetzen der Summe durch eine Integration.<br><br> | ||
| Zeile 181: | Zeile 189: | ||
::<math>{\rm Pr}(\tilde{x} = +1) = {\rm Pr}(\tilde{x} = -1) = 1/2 \hspace{0.05cm}. </math> | ::<math>{\rm Pr}(\tilde{x} = +1) = {\rm Pr}(\tilde{x} = -1) = 1/2 \hspace{0.05cm}. </math> | ||
| − | Damit erhält man | + | Damit erhält man für das Maximum der Transinformation, also für die Kanalkapazität: |
::<math>C \hspace{-0.15cm} = {1}/{2} \cdot \int_{-\infty }^{+ \infty} | ::<math>C \hspace{-0.15cm} = {1}/{2} \cdot \int_{-\infty }^{+ \infty} | ||
| Zeile 189: | Zeile 197: | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Das Integral lässt sich nicht in mathematisch–geschlossener Form lösen, sondern kann nur numerisch ausgewertet werden. Die grüne Kurve zeigt das Ergebnis. Die blaue Kurve gibt zum Vergleich die auf der letzten Seite hergeleitete Kanalkapazität für gaußverteilte Eingangssignale an. | + | Das Integral lässt sich nicht in mathematisch–geschlossener Form lösen, sondern kann nur numerisch ausgewertet werden. |
| + | *Die grüne Kurve zeigt das Ergebnis. | ||
| + | *Die blaue Kurve gibt zum Vergleich die auf der letzten Seite hergeleitete Kanalkapazität für gaußverteilte Eingangssignale an. | ||
| + | |||
| + | [[Datei:P ID2375 KC T 1 7 S4b v3.png|right|frame|AWGN–Kanalkapazität für binäre Eingangssignale|class=fit]] | ||
| + | |||
| − | |||
Man erkennt: | Man erkennt: | ||
| − | *Für $10 \cdot \lg \, E_{\rm B}/N_0 < 0 \, \rm dB$ unterscheiden sich die beiden Kapazitätskurven nur geringfügig. So muss man bei binärem bipolaren Eingang gegenüber dem Optimum (Gaußscher Eingang) die Kenngröße $10 \cdot \lg \, E_{\rm B}/N_0$ nur etwa um $0.1 \, \rm dB$ erhöhen, um ebenfalls die Coderate $R = 0.5$ zu ermöglichen.<br> | + | *Für $10 \cdot \lg \, E_{\rm B}/N_0 < 0 \, \rm dB$ unterscheiden sich die beiden Kapazitätskurven nur geringfügig. |
| + | *So muss man bei binärem bipolaren Eingang gegenüber dem Optimum (Gaußscher Eingang) die Kenngröße $10 \cdot \lg \, E_{\rm B}/N_0$ nur etwa um $0.1 \, \rm dB$ erhöhen, um ebenfalls die Coderate $R = 0.5$ zu ermöglichen.<br> | ||
| − | *Ab | + | *Ab $10 \cdot \lg \, E_{\rm B}/N_0 \approx6 \, \rm dB$ ist die Kapazität $C = 1 \, \rm bit/Kanalzugriff$ des AWGN–Kanals für binären Eingang (fast) erreicht. |
| + | *Dazwischen verläuft die Grenzkurve annähernd exponentiell ansteigend. | ||
| + | <br clear=all> | ||
| + | == Gebräuchliche Kanalcodes im Vergleich zur Kanalkapazität == | ||
| + | <br> | ||
| + | Nun soll gezeigt werden, in wie weit sich etablierte Kanalcodes der BPSK–Kanalkapazität (grüne Kurve) annähern. In der folgenden Grafik ist als Ordinate die Rate $R=k/n$ dieser Codes bzw. die Kapazität $C$ (mit der zusätzlichen Pseudo–Einheit „bit/Kanalzugriff”) aufgetragen. Weiter ist vorausgesetzt: | ||
| + | *der AWGN–Kanal, gekennzeichnet durch $10 \cdot \lg \, E_{\rm B}/N_0$ in dB, und<br> | ||
| + | *für die durch Kreuze markierten Codes eine Bitfehlerrate (BER) von $10^{-5}$.<br> | ||
| − | + | [[Datei:P ID2968 KC T 1 7 S5a v3.png|right|frame|Raten und erforderliches $E_{\rm B}/N_0$ verschiedener Kanalcodes|class=fit]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ||
$\text{Bitte beachten Sie:}$ | $\text{Bitte beachten Sie:}$ | ||
| − | *Die Kanalkapazitätskurven gelten stets für $n \to \infty$ und $\rm BER | + | *Die Kanalkapazitätskurven gelten stets für $n \to \infty$ und $\rm BER \to 0$ gelten. |
| − | *Würde man diese strenge Forderung „ | + | *Würde man diese strenge Forderung „fehlerfrei” auch an die betrachteten Kanalcodes endlicher Codelänge $n$ anlegen, so wäre hierfür stets $10 \cdot \lg \, E_{\rm B}/N_0 \to \infty$ erforderlich. |
| − | *Dies ist aber ein akademisches Problem, das für die Praxis wenig Bedeutung hat. Für $\rm BER = 10^{-10}$ ergäbe sich eine qualitativ ähnliche Grafik. | + | *Dies ist aber ein akademisches Problem, das für die Praxis wenig Bedeutung hat. Für $\rm BER = 10^{-10}$ ergäbe sich eine qualitativ und auch quantitativ ähnliche Grafik.<br> |
| − | + | <br clear=all> | |
Es folgen einige Erläuterungen zu den Daten, die der Vorlesung [Liv10]<ref name='Liv10'>Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.</ref> entnommen wurden: | Es folgen einige Erläuterungen zu den Daten, die der Vorlesung [Liv10]<ref name='Liv10'>Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.</ref> entnommen wurden: | ||
| + | *Die Punkte $\rm A$, $\rm B$ und $\rm C$ markieren [[Kanalcodierung/Beispiele_binärer_Blockcodes#Hamming.E2.80.93Codes|Hamming–Codes]] unterschiedlicher Rate. Sie alle benötigen für $\rm BER = 10^{-5}$ mehr alss $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$. | ||
| + | *Die Markierung $\rm D$ kennzeichnet den binären [https://de.wikipedia.org/wiki/Golay-Code Golay–Code] mit der Rate $1/2$ und die Markierung $\rm E$ einen [https://de.wikipedia.org/wiki/Reed-Muller-Code Reed–Muller–Code]. Dieser sehr niederratige Code kam bereits 1971 bei der Raumsonde Mariner 9 zum Einsatz. | ||
| + | *Die [[Kanalcodierung/Definition_und_Eigenschaften_von_Reed–Solomon–Codes|Reed–Solomon–Codes]] (RS–Codes) werden im zweiten Hauptkapitel ausführlich behandelt. Mit $\rm F$ markiert ist ein hochratiger RS–Code $(R = 223/255 > 0.9)$ und einem erforderlichen $10 \cdot \lg \, E_{\rm B}/N_0 < 6 \, \rm dB$. | ||
| + | *Die Markierungen $\rm G$ und $\rm H$ bezeichnen beispielhafte [[Kanalcodierung/Grundlagen_der_Faltungscodierung|Faltungscodes]] (englisch: <i>Convolutional Codes</i>, CC) mittlerer Rate. Der Code $\rm G$ wurde schon 1972 bei der Pioneer10–Mission eingesetzt. | ||
| + | *Die Kanalcodierung der Voyager–Mission Ende der 1970er Jahre ist mit $\rm I$ markiert. Es handelt sich um die Verkettung eines $\text{(2, 1, 7)}$–Faltungscodes mit einem Reed–Solomon–Code, wie im vierten Hauptkapitel beschrieben.<br><br> | ||
| − | + | ''Anmerkung'': Bei den Faltungscodes hat insbesondere der dritte Kennungsparameter eine andere Bedeutung als bei den Blockcodes. $\text{CC (2, 1, 32)}$ weist beispielsweise auf das Memory $m = 32$ hin.<br> | |
| − | + | [[Datei:P ID2377 KC T 1 7 S5b v4.png|right|frame|Raten und erforderliches $E_{\rm B}/N_0$ für iterative Codierverfahren |class=fit]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | + | Mit iterativer Decodierung lassen sich deutlich bessere Ergebnisse erzielen, wie die zweite Grafik zeigt. |
| + | *Das heißt: Die einzelnen Markierungspunkte liegen sehr viel näher an der Kapazitätskurve.<br> | ||
| + | *Die bisher mit „Gauß–Kapazität” beschriftete durchgezogene blaue Kurve wird hier „Gauß (reell)” genannt. | ||
| + | <br clear=all> | ||
| + | Hier noch einige weitere Erläuterungen zu dieser Grafik: | ||
| + | * Rote Kreuze markieren sogenannte [[Kanalcodierung/Grundlegendes_zu_den_Turbocodes|Turbocodes]] nach [https://en.wikipedia.org/wiki/Consultative_Committee_for_Space_Data_Systems CCSDS] (<i>Consultative Committee for Space Data Systems</i> ) mit jeweils $k = 6920$ Informationsbits und unterschiedlichen Codelängen $n$. Diese von [http://perso.telecom-bretagne.eu/claudeberrou/ Claude Berrou] um 1990 erfundenen Codes können iterativ decodiert werden. Die (roten) Markierungen liegen jeweils weniger als $1 \, \rm dB$ von der Shannon–Grenze entfernt.<br> | ||
| − | * | + | *Ähnliches Verhalten zeigen die durch weiße Rechtecke gekennzeichneten [[Kanalcodierung/Grundlegendes_zu_den_Low–density_Parity–check_Codes|LDPC–Codes]] (<i>Low Density Parity–check Codes</i> ), die seit 2006 bei [https://praxistipps.chip.de/dvb-s-und-dvb-s2-was-ist-der-unterschied_12879 DVB–S(2)] (<i>Digital Video Broadcast over Satellite</i> ) eingesetzt werden. Diese eignen sich aufgrund der spärlichen Belegung der Prüfmatrix $\boldsymbol {\rm H}$ (mit Einsen) sehr gut für die iterative Decodierung mittels ''Faktor–Graphen'' und ''Exit Charts''. Siehe [Hag02]<ref name='Hag02'>Hagenauer, J.: ''The Turbo Principle in Mobile Communications''. In: Int. Symp. on Information Theory and Its Applications, Oct.2010, [http://wwwmayr.in.tum.de/konferenzen/Jass05/courses/4/papers/prof_hagenauer.pdf PDF–Dokument.]</ref><br> |
| − | * | + | *Die schwarzen Punkte markieren die von CCSDS spezifizierten [[Kanalcodierung/Grundlegendes_zu_den_Low–density_Parity–check_Codes|LDPC–Codes]], die alle von einer konstanten Anzahl von Informationsbits ausgehen $(k = 16384)$. Dagegen ist bei allen weißen Rechtecken die Codelänge $n = 64800$ konstant, während sich die Anzahl $k$ der Informationsbits entsprechend der Rate $R = k/n$ ändert.<br> |
| + | *Um das Jahr 2000 hatten viele Forscher den Ehrgeiz, sich der Shannon–Grenze bis auf Bruchteile von einem $\rm dB$ anzunähern. Das gelbe Kreuz markiert ein solches Ergebnis aus [CFRU01]<ref name='CFRU01'>Chung S.Y; Forney Jr., G.D.; Richardson, T.J.; Urbanke, R.: ''On the Design of Low-Density Parity- Check Codes within 0.0045 dB of the Shannon Limit''. – In: IEEE Communications Letters, vol. 5, no. 2 (2001), pp. 58–60.''</ref>. Verwendet wurde ein irregulärer Rate–1/2–LDPC–Code der Codelänge $n = 2 \cdot10^6$.<br><br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Fazit:}$ Festzuhalten ist, dass Shannon bereits 1948 erkannt und nachgewiesen hat, dass kein eindimensionales Modulationsverfahren links von der durchgehend eingezeichneten AWGN–Grenzkurve „Gauß (reell)” liegen kann. | $\text{Fazit:}$ Festzuhalten ist, dass Shannon bereits 1948 erkannt und nachgewiesen hat, dass kein eindimensionales Modulationsverfahren links von der durchgehend eingezeichneten AWGN–Grenzkurve „Gauß (reell)” liegen kann. | ||
*Für zweidimensionale Verfahren wie QAM und mehrstufige PSK gilt dagegen die Grenzkurve „Gauß (komplex)”, die hier gestrichelt gezeichnet ist und stets links von der durchgezogenen Kurve liegt. | *Für zweidimensionale Verfahren wie QAM und mehrstufige PSK gilt dagegen die Grenzkurve „Gauß (komplex)”, die hier gestrichelt gezeichnet ist und stets links von der durchgezogenen Kurve liegt. | ||
| − | *Näheres hierzu finden Sie im Abschnitt | + | *Näheres hierzu finden Sie im Abschnitt [[Informationstheorie/AWGN%E2%80%93Kanalkapazit%C3%A4t_bei_wertdiskretem_Eingang#Maximale_Coderate_f.C3.BCr_QAM.E2.80.93Strukturen|Maximale Coderate für QAM–Strukturen]] des Buches „Informationstheorie”.<br> |
*Auch diese Grenzkurve wurde mit QAM–Verfahren und sehr langen Kanalcodes inzwischen nahezu erreicht, ohne dass sie jemals überschritten werden wird.}}<br> | *Auch diese Grenzkurve wurde mit QAM–Verfahren und sehr langen Kanalcodes inzwischen nahezu erreicht, ohne dass sie jemals überschritten werden wird.}}<br> | ||
== Aufgaben zum Kapitel == | == Aufgaben zum Kapitel == | ||
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.17:_Zum_Kanalcodierungstheorem|Aufgabe 1.17: Zum Kanalcodierungstheorem]] |
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.17Z:_BPSK–Kanalkapazität|Aufgabe 1.17Z: BPSK–Kanalkapazität]] |
==Quellenverzeichnis== | ==Quellenverzeichnis== | ||
Aktuelle Version vom 18. August 2022, 15:17 Uhr
Inhaltsverzeichnis
Kanalcodierungstheorem und Kanalkapazität
Wir betrachten weiterhin einen binären Blockcode mit $k$ Informationsbits pro Block und Codeworte der Länge $n$, woraus sich die Coderate $R=k/n$ mit der Einheit „Informationsbit/Codesymbol” ergibt.
Der geniale Informationstheoretiker Claude E. Shannon hat sich schon 1948 sehr intensiv mit der Korrekturfähigkeit solcher Codes beschäftigt und hierfür für jeden Kanal eine Grenze angegeben, die sich allein aus informationstheoretischen Überlegungen ergibt. Bis heute wurde noch kein Code gefunden, der diese Grenze übersteigt, und dies wird auch so bleiben.
$\text{Shannons Kanalcodierungstheorem:}$ Zu jedem Kanal mit der Kanalkapazität $C > 0$ existiert stets (mindestens) ein Code, dessen Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R$ kleiner ist als die Kanalkapazität $C$. Voraussetzung hierfür ist, dass für die Blocklänge dieses Codes gilt: $n \to \infty$.
Anmerkungen:
- Die Aussage „Die Fehlerwahrscheinlichkeit geht gegen Null” ist nicht identisch mit der Aussage „Die Übertragung ist fehlerfrei”. Beispiel: Bei einer unendlich langen Folge werden endlich viele Symbole verfälscht.
- Bei manchen Kanälen geht auch mit $R=C$ die Fehlerwahrscheinlichkeit noch gegen Null (aber nicht bei allen).
Die Umkehrung des Kanalcodierungstheorems ist ebenfalls zutreffend und besagt:
$\text{Umkehrschluss:}$ Ist die Coderate $R$ größer als die Kanalkapazität $C$, so kann eine beliebig kleine Fehlerwahrscheinlichkeit auf keinen Fall erreicht werden.
Zur Herleitung und Berechnung der Kanalkapazität gehen wir zunächst von einem digitalen Kanal mit $M_x$ möglichen Eingangswerten $x$ und $M_y$ möglichen Ausgangswerten $y$ aus. Dann gilt für den mittleren Transinformationsgehalt – kurz die Transinformation (englisch: Mutual Information) – zwischen der Zufallsgröße $x$ am Kanaleingang und der Zufallsgröße $y$ an seinem Ausgang:
- \[I(x; y) =\sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y} \hspace{0.15cm}{\rm Pr}(x_i, y_j) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{{\rm Pr}(y_j)} = \sum_{i= 1 }^{M_X} \hspace{0.15cm}\sum_{j= 1 }^{M_Y}\hspace{0.15cm}{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i) \cdot {\rm Pr}(x_i) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_i)}{\sum_{k= 1}^{M_X} {\rm Pr}(y_j \hspace{0.05cm}| \hspace{0.05cm}x_k) \cdot {\rm Pr}(x_k)} \hspace{0.05cm}.\]
Beim Übergang von der ersten zur zweiten Gleichung wurden dabei der Satz von Bayes sowie der Satz von der totalen Wahrscheinlichkeit berücksichtigt.
Weiter ist anzumerken:
- Der Logarithmus dualis ist hier mit „log2” bezeichnet ist. Teilweise verwenden wir in unserem Lerntutorial hierfür auch „ld”.
- Im Gegensatz zum Buch Informationstheorie unterscheiden wir im Folgenden nicht zwischen der Zufallsgröße $($Großbuchstaben $X$ bzw. $Y)$ und den Realisierungen $($Kleinbuchstaben $x$ bzw. $y)$.
$\text{Definition:}$ Die von Shannon eingeführte Kanalkapazität gibt die maximale Transinformation $I(x; y)$ zwischen der Eingangsgröße $x$ und der Ausgangsgröße $y$ an:
- \[C = \max_{{{\rm Pr}(x_i)}} \hspace{0.1cm} I(X; Y) \hspace{0.05cm}.\]
Hinzugefügt werden muss die Pseudo–Einheit „bit/Kanalzugriff”.
Da die Maximierung der Transinformation über alle möglichen (diskreten) Eingangsverteilungen ${\rm Pr}(x_i)$ erfolgen muss, ist die Kanalkapazität unabhängig vom Eingang und damit eine reine Kanalkenngröße.
Kanalkapazität des BSC–Modells
Wir wenden nun diese Definitionen auf das BSC–Modell (Binary Symmetric Channel ) an:
- \[I(x; y) = {\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 0 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 0)} + {\rm Pr}(y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0) \cdot {\rm Pr}(x = 0) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 1 \hspace{0.03cm}| \hspace{0.03cm}x = 0)}{{\rm Pr}(y = 1)} + \]
- \[\hspace{1.45cm} + \hspace{0.15cm}{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(Y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1)}{{\rm Pr}(y = 0)} + {\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1) \cdot {\rm Pr}(x = 1) \cdot {\rm log_2 } \hspace{0.15cm}\frac{{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1)}{{\rm Pr}(y = 1)} \hspace{0.05cm}.\]
Zur Kanalkapazität gelangt man durch folgende Überlegungen:
- Die Maximierung bezüglich der Eingangsverteilung führt auf gleichwahrscheinliche Symbole:
- \[{\rm Pr}(x = 0) = {\rm Pr}(x = 1) = 1/2 \hspace{0.05cm}.\]
- Aufgrund der aus dem Modell erkennbaren Symmetrie gilt dann gleichzeitig:
- \[{\rm Pr}(y = 0) = {\rm Pr}(y = 1) = 1/2 \hspace{0.05cm}.\]
- Wir berücksichtigen zudem die BSC–Übergangswahrscheinlichkeiten:
- \[{\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = \varepsilon \hspace{0.05cm},\]
- \[{\rm Pr}(y = 0 \hspace{0.05cm}| \hspace{0.05cm}x = 0) = {\rm Pr}(y = 1 \hspace{0.05cm}| \hspace{0.05cm}x = 1) = 1-\varepsilon \hspace{0.05cm}.\]
- Nach Zusammenfassen je zweier Terme erhält man somit:
- \[C \hspace{0.15cm} = \hspace{0.15cm} 2 \cdot 1/2 \cdot \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{\varepsilon}{1/2 }+ 2 \cdot 1/2 \cdot (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1- \varepsilon}{1/2 } \varepsilon \cdot {\rm ld } \hspace{0.15cm}2 - \varepsilon \cdot {\rm log_2 } \hspace{0.15cm} \frac{1}{\varepsilon }+ (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm} 2 - (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\]
- \[\Rightarrow \hspace{0.3cm} C \hspace{0.15cm} = \hspace{0.15cm} 1 - H_{\rm bin}(\varepsilon). \]
- Verwendet ist hier die binäre Entropiefunktion:
- \[H_{\rm bin}(\varepsilon) = \varepsilon \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{\varepsilon}+ (1- \varepsilon) \cdot {\rm log_2 } \hspace{0.15cm}\frac{1}{1- \varepsilon}\hspace{0.05cm}.\]
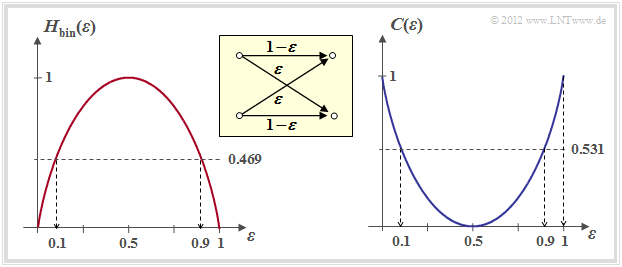
Die folgende rechte Grafik zeigt die BSC–Kanalkapazität abhängig von der Verfälschungswahrscheinlichkeit $\varepsilon$. Links ist zum Vergleich die binäre Entropiefunktion dargestellt, die bereits im Kapitel Gedächtnislose Nachrichtenquellen des Buches „Informationstheorie” definiert wurde.
Man erkennt aus dieser Darstellung:
- Die Verfälschungswahrscheinlichkeit $\varepsilon$ führt zur Kanalkapazität $C(\varepsilon)$. Eine fehlerfreie Decodierung nach bestmöglicher Codierung ist nach dem Kanalcodierungstheorem nur dann möglich, wenn die Coderate $R$ nicht größer ist als $C(\varepsilon)$.
- Mit $\varepsilon = 10\%$ ist wegen $C(0.1) = 0.531$ eine fehlerfreie Decodierung nicht möglich, wenn die Coderate $R > 0.531$ beträgt. Bei 50–prozentiger Verfälschung ist eine fehlerfreie Decodierung auch bei beliebig kleiner Coderate unmöglich: $C(0.5) = 0$ .
- Aus informationstheoretischer Sicht ist $\varepsilon = 1$ (Invertierung aller Bits) gleich gut wie $\varepsilon = 0$ (fehlerfreie Übertragung). Ebenso ist $\varepsilon = 0.9$ äquivalent zu $\varepsilon = 0.1$. Eine fehlerfreie Decodierung erzielt man hier durch Vertauschen der Nullen und Einsen, also durch ein so genanntes Mapping.
Kanalkapazität des AWGN–Modells
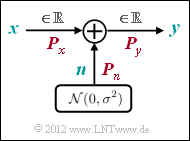
Wir betrachten nun den AWGN–Kanal (Additive White Gaussian Noise ). Hier gilt für das Ausgangssignal $y = x + n$, wobei $n$ eine gaußverteilte Zufallsgröße beschreibt, und es gilt für deren Erwartungswerte (Momente):
- $${\rm E}[n] = 0,\hspace{1cm} {\rm E}[n^2] = P_n.$$
Damit ergibt sich unabhängig vom Eingangssignal $x$ (analog oder digital) stets ein wertkontinuierliches Ausgangssignal $y$, und in der Gleichung für die Transinformation ist $M_y \to\infty$ einzusetzen.
Die Berechnung der Kanalkapazität für den AWGN–Kanal wird hier nur in Stichworten angegeben. Die genaue Herleitung finden Sie im vierten Hauptkapitel „Wertdiskrete Informationstheorie” des Buches Informationstheorie.
- Die im Hinblick auf maximale Transinformation optimierte Eingangsgröße $x$ wird mit Sicherheit wertkontinuierlich sein, das heißt, beim AWGN–Kanal gilt außer $M_y \to\infty$ auch $M_x \to\infty$.
- Während bei wertdiskretem Eingang über alle ${\rm Pr}(x_i)$ zu optimieren ist, erfolgt nun die Optimierung anhand der WDF $f_x(x)$ des Eingangssignals unter der Nebenbedingung Leistungsbegrenzung:
- \[C = \max_{f_x(x)} \hspace{0.1cm} I(x; y)\hspace{0.05cm},\hspace{0.3cm}{\rm wobei \hspace{0.15cm} gelten \hspace{0.15cm} muss} \text{:}\hspace{0.15cm} {\rm E} \left [ x^2 \right ] \le P_x \hspace{0.05cm}.\]
- Die Optimierung liefert für die Eingangs–WDF ebenfalls eine Gaußverteilung ⇒ $x$, $n$ und $y$ sind gaußverteilt gemäß den Dichtefunktionen $f_x(x)$, $f_n(n)$ und $f_y(y)$. Die entsprechenden Leistungen benennen wir $P_x$, $P_n$ und $P_y$.
- Nach längerer Rechnung erhält man für die Kanalkapazität unter Verwendung des Logarithmus dualis $\log_2(\cdot)$ – wiederum mit der Pseudo–Einheit „bit/Kanalzugriff”:
- \[C = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_y}{P_n }} = {\rm log_2 } \hspace{0.15cm} \sqrt{\frac{P_x + P_n}{P_n }} = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + \frac{P_x}{P_n } \right )\hspace{0.05cm}.\]
- Beschreibt $x$ ein zeitdiskretes Signal mit der Symbolrate $1/T_{\rm S}$, so muss dieses auf $B = 1/(2T_{\rm S})$ bandbegrenzt sein, und die gleiche Bandbreite $B$ muss man auch für das Rauschsignal $n$ ansetzen ⇒ „Rauschbandbreite”:
- \[P_X = \frac{E_{\rm S}}{T_{\rm S} } \hspace{0.05cm}, \hspace{0.4cm} P_N = \frac{N_0}{2T_{\rm S} }\hspace{0.05cm}. \]
- Somit lässt sich die AWGN–Kanalkapazität auch durch die Sendeenergie pro Symbol $(E_{\rm S})$ und die Rauschleistungsdichte $(N_0)$ ausdrücken:
- \[C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{1.9cm} \text {Einheit:}\hspace{0.3cm} \frac{\rm bit}{\rm Kanalzugriff}\hspace{0.05cm}.\]
- Mit der folgenden Gleichung erhält man die Kanalkapazität pro Zeiteinheit (Kennzeichnung durch $^{\star})$:
- \[C^{\star} = \frac{C}{T_{\rm S} } = B \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 + {2 E_{\rm S}}/{N_0 } \right )\hspace{0.05cm}, \hspace{0.8cm}
\text {Einheit:} \hspace{0.3cm} \frac{\rm bit}{\rm Zeiteinheit}\hspace{0.05cm}.\]
$\text{Beispiel 1:}$
- Für $E_{\rm S}/N_0 = 7.5$ ⇒ $10 \cdot \lg \, E_{\rm S}/N_0 = 8.75 \, \rm dB$ erhält man die Kanalkapazität $C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm} (16) = 2 \, \rm bit/Kanalzugriff$.
- Bei einem Kanal mit der (physikalischen) Bandbreite $B = 4 \, \rm kHz$, was der Abtastrate $f_{\rm A} = 8\, \rm kHz$ entspricht, gilt zudem $C^\star = 16 \, \rm kbit/s$.
Ein Vergleich verschiedener Codierverfahren bei konstantem $E_{\rm S}$ (Energie pro übertragenem Symbol ) ist allerdings nicht fair. Vielmehr sollte man für diesen Vergleich die Energie $E_{\rm B}$ pro Nutzbit fest vorgeben. Dabei gelten folgende Zusammenhänge:
- \[E_{\rm S} = R \cdot E_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} E_{\rm B} = E_{\rm S} / R \hspace{0.05cm}. \]
$\text{Kanalcodierungstheorem für den AWGN–Kanal:}$
Eine fehlerfreie Decodierung $($bei unendlich langen Blöcken ⇒ $n \to \infty)$ ist immer dann möglich, falls die Coderate $R$ kleiner ist als die Kanalkapazität $C$:
- \[R < C = {1}/{2 } \cdot {\rm log_2 } \hspace{0.05cm}\left ( 1 +2 \cdot R\cdot E_{\rm B}/{N_0 } \right )\hspace{0.05cm}.\]
Für jede Coderate  $R$ lässt sich damit das erforderliche $E_{\rm B}/N_0$ des AWGN–Kanals ermitteln, damit eine fehlerfreie Decodierung gerade noch möglich ist. Man erhält für den Grenzfall $R = C$:
- \[{E_{\rm B} }/{N_0} > \frac{2^{2R}-1}{2R } \hspace{0.05cm}.\]
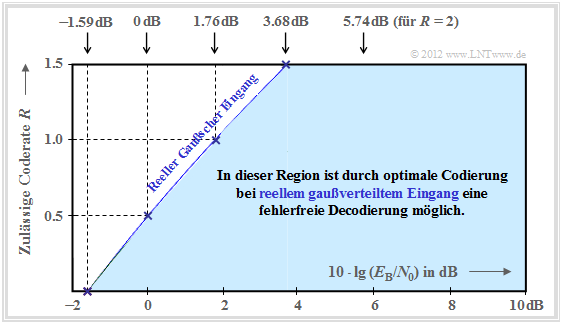
Die Grafik fasst das Ergebnis zusammen, wobei die Ordinate $R$ im linearen Maßstab und die Abszisse $E_{\rm B}/{N_0 }$ logarithmisch aufgetragen ist.
- Außerhalb der blauen Fläche ist eine fehlerfreie Codierung nicht möglich.
- Die blaue Grenzkurve gibt die Kanalkapazität $C$ des AWGN–Kanals an.
Aus dieser Grafik und obiger Gleichung lässt sich Folgendes ableiten:
- Die Kanalkapazität $C$ steigt etwas weniger als linear mit $10 \cdot \lg \, E_{\rm B}/N_0 $ an. In der Grafik sind einige ausgewählte Funktionswerte als blaue Kreuze angegeben.
- Ist $10 \cdot \lg \, E_{\rm B}/N_0 < -1.59 \, \rm dB$, so ist eine fehlerfreie Decodierung prinzipiell unmöglich. Beträgt die Coderate $R = 0.5$, so muss $10 \cdot \lg \, E_{\rm B}/N_0 > 0 \, \rm dB$ sein ⇒ $E_{\rm B} > N_0$.
- Für alle binären Codes gilt per se $0 < R ≤ 1$. Nur mit nichtbinären Codes sind Coderaten $R > 1$ möglich. Beispielsweise beträgt die maximal mögliche Coderate eines quaternären Codes $R = \log_2 \, M_y = \log_2 \, 4 = 2$.
- Alle eindimensionalen Modulationsarten – also solche Verfahren, die nur die Inphase– oder nur die Quadraturkomponente nutzen wie 2–ASK, BPSK und 2–FSK – müssen im blauen Bereich der vorliegenden Grafik liegen.
- Wie im Kapitel Maximale Coderate für QAM–Strukturen des Buches „Informationstheorie” gezeigt wird, gibt es für zweidimensionale Modulationsarten wie zum Beispiel die Quadratur–Amplitudenmodulation eine „freundlichere” Grenzkurve.
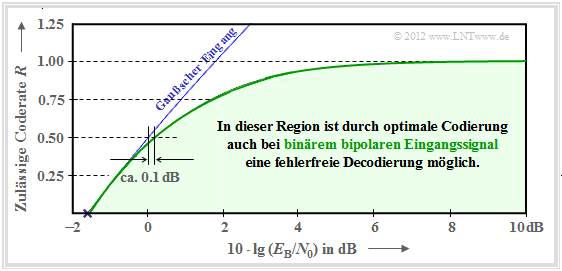
AWGN–Kanalkapazität für binäre Eingangssignale
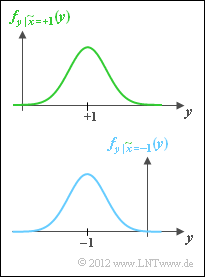
In diesem Buch beschränken wir uns vorwiegend auf binäre Codes, also auf das Galoisfeld ${\rm GF}(2^n)$. Damit ist
- zum einen die Coderate auf den Bereich $R ≤ 1$ begrenzt,
- zum zweiten auch für $R ≤ 1$ nicht die gesamte blaue Region verfügbar (siehe vorherige Seite).
Die nun gültige Region ergibt sich aus der allgemeinen Gleichung der Transinformation durch
- die Parameter $M_x = 2$ und $M_y \to \infty$,
- bipolare Signalisierung ⇒ $x=0$ → $\tilde{x} = +1$ und $x=1$ → $\tilde{x} = -1$,
- den Übergang von bedingten Wahrscheinlichkeiten ${\rm Pr}(\tilde{x}_i)$ zu bedingten Wahrscheinlichkeitsdichtefunktionen,
- Ersetzen der Summe durch eine Integration.
Die Optimierung der Quelle führt auf gleichwahrscheinliche Symbole:
- \[{\rm Pr}(\tilde{x} = +1) = {\rm Pr}(\tilde{x} = -1) = 1/2 \hspace{0.05cm}. \]
Damit erhält man für das Maximum der Transinformation, also für die Kanalkapazität:
- \[C \hspace{-0.15cm} = {1}/{2} \cdot \int_{-\infty }^{+ \infty} \left [ f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = +1}(y)\cdot {\rm log_2 } \hspace{0.15cm}\frac {f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = +1}(y)}{f_y(y)} + f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = -1}(y)\cdot {\rm log_2 } \hspace{0.15cm}\frac {f_{y\hspace{0.05cm} |\hspace{0.05cm}\tilde{x} = -1}(y)}{f_y(y)} \right ]\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.\]
Das Integral lässt sich nicht in mathematisch–geschlossener Form lösen, sondern kann nur numerisch ausgewertet werden.
- Die grüne Kurve zeigt das Ergebnis.
- Die blaue Kurve gibt zum Vergleich die auf der letzten Seite hergeleitete Kanalkapazität für gaußverteilte Eingangssignale an.
Man erkennt:
- Für $10 \cdot \lg \, E_{\rm B}/N_0 < 0 \, \rm dB$ unterscheiden sich die beiden Kapazitätskurven nur geringfügig.
- So muss man bei binärem bipolaren Eingang gegenüber dem Optimum (Gaußscher Eingang) die Kenngröße $10 \cdot \lg \, E_{\rm B}/N_0$ nur etwa um $0.1 \, \rm dB$ erhöhen, um ebenfalls die Coderate $R = 0.5$ zu ermöglichen.
- Ab $10 \cdot \lg \, E_{\rm B}/N_0 \approx6 \, \rm dB$ ist die Kapazität $C = 1 \, \rm bit/Kanalzugriff$ des AWGN–Kanals für binären Eingang (fast) erreicht.
- Dazwischen verläuft die Grenzkurve annähernd exponentiell ansteigend.
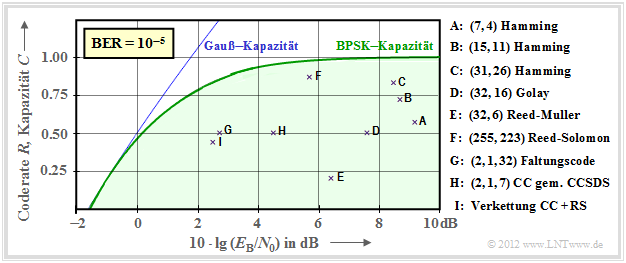
Gebräuchliche Kanalcodes im Vergleich zur Kanalkapazität
Nun soll gezeigt werden, in wie weit sich etablierte Kanalcodes der BPSK–Kanalkapazität (grüne Kurve) annähern. In der folgenden Grafik ist als Ordinate die Rate $R=k/n$ dieser Codes bzw. die Kapazität $C$ (mit der zusätzlichen Pseudo–Einheit „bit/Kanalzugriff”) aufgetragen. Weiter ist vorausgesetzt:
- der AWGN–Kanal, gekennzeichnet durch $10 \cdot \lg \, E_{\rm B}/N_0$ in dB, und
- für die durch Kreuze markierten Codes eine Bitfehlerrate (BER) von $10^{-5}$.
$\text{Bitte beachten Sie:}$
- Die Kanalkapazitätskurven gelten stets für $n \to \infty$ und $\rm BER \to 0$ gelten.
- Würde man diese strenge Forderung „fehlerfrei” auch an die betrachteten Kanalcodes endlicher Codelänge $n$ anlegen, so wäre hierfür stets $10 \cdot \lg \, E_{\rm B}/N_0 \to \infty$ erforderlich.
- Dies ist aber ein akademisches Problem, das für die Praxis wenig Bedeutung hat. Für $\rm BER = 10^{-10}$ ergäbe sich eine qualitativ und auch quantitativ ähnliche Grafik.
Es folgen einige Erläuterungen zu den Daten, die der Vorlesung [Liv10][1] entnommen wurden:
- Die Punkte $\rm A$, $\rm B$ und $\rm C$ markieren Hamming–Codes unterschiedlicher Rate. Sie alle benötigen für $\rm BER = 10^{-5}$ mehr alss $10 \cdot \lg \, E_{\rm B}/N_0 = 8 \, \rm dB$.
- Die Markierung $\rm D$ kennzeichnet den binären Golay–Code mit der Rate $1/2$ und die Markierung $\rm E$ einen Reed–Muller–Code. Dieser sehr niederratige Code kam bereits 1971 bei der Raumsonde Mariner 9 zum Einsatz.
- Die Reed–Solomon–Codes (RS–Codes) werden im zweiten Hauptkapitel ausführlich behandelt. Mit $\rm F$ markiert ist ein hochratiger RS–Code $(R = 223/255 > 0.9)$ und einem erforderlichen $10 \cdot \lg \, E_{\rm B}/N_0 < 6 \, \rm dB$.
- Die Markierungen $\rm G$ und $\rm H$ bezeichnen beispielhafte Faltungscodes (englisch: Convolutional Codes, CC) mittlerer Rate. Der Code $\rm G$ wurde schon 1972 bei der Pioneer10–Mission eingesetzt.
- Die Kanalcodierung der Voyager–Mission Ende der 1970er Jahre ist mit $\rm I$ markiert. Es handelt sich um die Verkettung eines $\text{(2, 1, 7)}$–Faltungscodes mit einem Reed–Solomon–Code, wie im vierten Hauptkapitel beschrieben.
Anmerkung: Bei den Faltungscodes hat insbesondere der dritte Kennungsparameter eine andere Bedeutung als bei den Blockcodes. $\text{CC (2, 1, 32)}$ weist beispielsweise auf das Memory $m = 32$ hin.
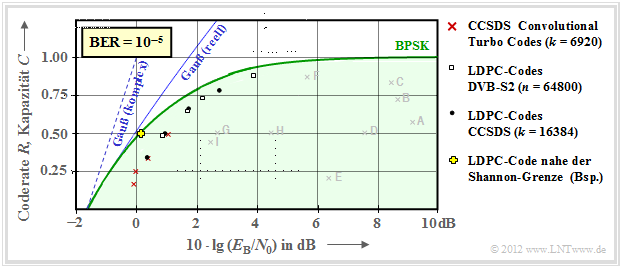
Mit iterativer Decodierung lassen sich deutlich bessere Ergebnisse erzielen, wie die zweite Grafik zeigt.
- Das heißt: Die einzelnen Markierungspunkte liegen sehr viel näher an der Kapazitätskurve.
- Die bisher mit „Gauß–Kapazität” beschriftete durchgezogene blaue Kurve wird hier „Gauß (reell)” genannt.
Hier noch einige weitere Erläuterungen zu dieser Grafik:
- Rote Kreuze markieren sogenannte Turbocodes nach CCSDS (Consultative Committee for Space Data Systems ) mit jeweils $k = 6920$ Informationsbits und unterschiedlichen Codelängen $n$. Diese von Claude Berrou um 1990 erfundenen Codes können iterativ decodiert werden. Die (roten) Markierungen liegen jeweils weniger als $1 \, \rm dB$ von der Shannon–Grenze entfernt.
- Ähnliches Verhalten zeigen die durch weiße Rechtecke gekennzeichneten LDPC–Codes (Low Density Parity–check Codes ), die seit 2006 bei DVB–S(2) (Digital Video Broadcast over Satellite ) eingesetzt werden. Diese eignen sich aufgrund der spärlichen Belegung der Prüfmatrix $\boldsymbol {\rm H}$ (mit Einsen) sehr gut für die iterative Decodierung mittels Faktor–Graphen und Exit Charts. Siehe [Hag02][2]
- Die schwarzen Punkte markieren die von CCSDS spezifizierten LDPC–Codes, die alle von einer konstanten Anzahl von Informationsbits ausgehen $(k = 16384)$. Dagegen ist bei allen weißen Rechtecken die Codelänge $n = 64800$ konstant, während sich die Anzahl $k$ der Informationsbits entsprechend der Rate $R = k/n$ ändert.
- Um das Jahr 2000 hatten viele Forscher den Ehrgeiz, sich der Shannon–Grenze bis auf Bruchteile von einem $\rm dB$ anzunähern. Das gelbe Kreuz markiert ein solches Ergebnis aus [CFRU01][3]. Verwendet wurde ein irregulärer Rate–1/2–LDPC–Code der Codelänge $n = 2 \cdot10^6$.
$\text{Fazit:}$ Festzuhalten ist, dass Shannon bereits 1948 erkannt und nachgewiesen hat, dass kein eindimensionales Modulationsverfahren links von der durchgehend eingezeichneten AWGN–Grenzkurve „Gauß (reell)” liegen kann.
- Für zweidimensionale Verfahren wie QAM und mehrstufige PSK gilt dagegen die Grenzkurve „Gauß (komplex)”, die hier gestrichelt gezeichnet ist und stets links von der durchgezogenen Kurve liegt.
- Näheres hierzu finden Sie im Abschnitt Maximale Coderate für QAM–Strukturen des Buches „Informationstheorie”.
- Auch diese Grenzkurve wurde mit QAM–Verfahren und sehr langen Kanalcodes inzwischen nahezu erreicht, ohne dass sie jemals überschritten werden wird.
Aufgaben zum Kapitel
Aufgabe 1.17: Zum Kanalcodierungstheorem
Aufgabe 1.17Z: BPSK–Kanalkapazität
Quellenverzeichnis
- ↑ Liva, G.: Channel Coding. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, TU München und DLR Oberpfaffenhofen, 2010.
- ↑ Hagenauer, J.: The Turbo Principle in Mobile Communications. In: Int. Symp. on Information Theory and Its Applications, Oct.2010, PDF–Dokument.
- ↑ Chung S.Y; Forney Jr., G.D.; Richardson, T.J.; Urbanke, R.: On the Design of Low-Density Parity- Check Codes within 0.0045 dB of the Shannon Limit. – In: IEEE Communications Letters, vol. 5, no. 2 (2001), pp. 58–60.