Aufgaben:Aufgabe 3.1: Kausalitätsbetrachtungen: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 3.1 Kausalitätsbetrachtungen nach Aufgabe 3.1: Kausalitätsbetrachtungen) |
|||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1755__LZI_A_3_1.png|right|Zwei Vierpolschaltungen]] | + | [[Datei:P_ID1755__LZI_A_3_1.png|right|frame|Zwei Vierpolschaltungen]] |
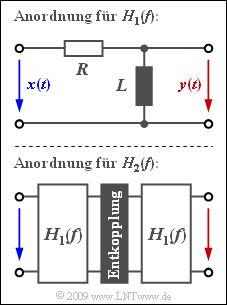
Die Grafik zeigt oben den Vierpol mit der Übertragungsfunktion | Die Grafik zeigt oben den Vierpol mit der Übertragungsfunktion | ||
| − | $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} | + | :$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | wobei $f_{\rm G}$ die 3dB–Grenzfrequenz angibt: | + | wobei $f_{\rm G}$ die 3dB–Grenzfrequenz angibt: |
| − | $$f_{\rm G} = \frac{R}{2 \pi \cdot L} | + | :$$f_{\rm G} = \frac{R}{2 \pi \cdot L} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Durch Hintereinanderschalten $n$ gleich | + | Durch Hintereinanderschalten von $n$ gleich aufgebauten Vierpolen $H_1(f)$ kommt man zur Übertragungsfunktion |
| − | $$H_n(f) = \ | + | :$$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Vorausgesetzt ist hierbei eine geeignete Widerstandsentkopplung, die aber zur Lösung dieser Aufgabe nicht von Bedeutung ist. Die untere Grafik zeigt zum Beispiel die Realisierung der Übertragungsfunktion $H_2(f)$. | + | *Vorausgesetzt ist hierbei eine geeignete Widerstandsentkopplung, die aber zur Lösung dieser Aufgabe nicht von Bedeutung ist. |
| + | *Die untere Grafik zeigt zum Beispiel die Realisierung der Übertragungsfunktion $H_2(f)$. | ||
| − | In dieser Aufgabe wird ein solcher Vierpol im Hinblick auf seine Kausalitätseigenschaften betrachtet. Bei einem jeden kausalen System erfüllen der Real– und der Imaginärteil der Spektralfunktion $H(f)$ die [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Hilbert–Transformation]], was durch das folgende Kurzzeichen ausgedrückt wird: | + | |
| − | $${\rm Im} \left\{ H(f) \right \} \quad | + | In dieser Aufgabe wird ein solcher Vierpol im Hinblick auf seine Kausalitätseigenschaften betrachtet. |
| + | |||
| + | Bei einem jeden kausalen System erfüllen der Real– und der Imaginärteil der Spektralfunktion $H(f)$ die [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Hilbert–Transformation]], was durch das folgende Kurzzeichen ausgedrückt wird: | ||
| + | :$${\rm Im} \left\{ H(f) \right \} \quad | ||
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
{\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$ | ||
| − | Da die Hilbert–Transformation nicht nur für Übertragungsfunktionen, sondern auch für Zeitsignale wichtige Aussagen liefert, wird die Korrespondenz häufig durch die allgemeine Variable $x$ ausgedrückt, die je nach Anwendungsfall als normierte Frequenz oder als normierte Zeit zu interpretieren ist. | + | Da die Hilbert–Transformation nicht nur für Übertragungsfunktionen, sondern auch für Zeitsignale wichtige Aussagen liefert, wird die Korrespondenz häufig durch die allgemeine Variable $x$ ausgedrückt, die je nach Anwendungsfall als normierte Frequenz oder als normierte Zeit zu interpretieren ist. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz|Folgerungen aus dem Zuordnungssatz]]. | + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz|Folgerungen aus dem Zuordnungssatz]]. |
| − | *Bezug genommen wird auch auf die Therieseiten [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Hilbert-Transformation]] sowie [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Partialbruchzerlegung|Partialbruchzerlegung]]. | + | *Bezug genommen wird auch auf die Therieseiten [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Hilbert-Transformation]] sowie [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Partialbruchzerlegung|Partialbruchzerlegung]]. |
| − | + | ||
| Zeile 34: | Zeile 45: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie kann $H_1(f)$ charakterisiert werden? | + | {Wie kann $H_1(f)$ charakterisiert werden? |
| − | |type=" | + | |type="()"} |
| − | - $H_1(f)$ beschreibt einen Tiefpass. | + | - $H_1(f)$ beschreibt einen Tiefpass. |
| − | + $H_1(f)$ beschreibt einen Hochpass. | + | + $H_1(f)$ beschreibt einen Hochpass. |
| − | {Beschreibt $H_1(f)$ ein kausales Netzwerk? | + | {Beschreibt $H_1(f)$ ein kausales Netzwerk? |
| − | |type=" | + | |type="()"} |
+ Ja. | + Ja. | ||
- Nein. | - Nein. | ||
| − | {Berechnen Sie die Übertragungsfunktion $H_2(f)$. Welcher komplexe Wert ergibt sich für $f = f_{\rm G} | + | {Berechnen Sie die Übertragungsfunktion $H_2(f)$. Welcher komplexe Wert ergibt sich für $f = f_{\rm G}$? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Re} | + | ${\rm Re}\big[H_2(f = f_{\rm G})\big] \ = \ $ { 0. } |
| − | ${\rm Im} | + | ${\rm Im}\big[H_2(f = f_{\rm G})\big] \ = \ $ { 0.5 3% } |
| − | {Welche der | + | {Welche der folgenden Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
| − | + $H_2(f)$ beschreibt ein kausales System. | + | + $H_2(f)$ beschreibt ein kausales System. |
| − | + $(x^4 - x^2)/(x^4 +2 x^2 + 1)$ und $2x^3/(x^4 +2 x^2 + 1)$ sind ein Hilbert–Paar. | + | + Die Ausdrücke $(x^4 - x^2)/(x^4 +2 x^2 + 1)$ und $2x^3/(x^4 +2 x^2 + 1)$ sind ein Hilbert–Paar. |
| − | - Für $n > 2$ ist die Kausalitätsbedingung nicht erfüllt. | + | - Für $n > 2$ ist die Kausalitätsbedingung nicht erfüllt. |
| Zeile 64: | Zeile 75: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: |
| − | $$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1$$ | + | *Die angegebene Übertragungsfunktion kann man nach dem Spannungsteilerprinzip berechnen. Es gilt: |
| + | :$$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1.$$ | ||
| + | *Es handelt sich um einen Hochpass. | ||
| + | *Für sehr niedrige Frequenzen stellt die Induktivität $L$ einen Kurzschluss dar. | ||
| − | |||
| − | '''(2)''' Jedes reale Netzwerk ist kausal. Die Impulsantwort $h(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn zum Zeitpunkt $t= 0$ am Eingang ein extrem kurzfristiger Impuls – ein so genannter Diracimpuls – angelegt wird. Aus Kausalitätsgründen kann dann natürlich am Ausgang nicht schon für Zeiten $t< 0$ ein Signal auftreten: | + | '''(2)''' Richtig ist <u>Ja</u>: |
| − | $$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | + | *Jedes reale Netzwerk ist kausal. Die Impulsantwort $h(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn zum Zeitpunkt $t= 0$ am Eingang ein extrem kurzfristiger Impuls – ein so genannter Diracimpuls – angelegt wird. |
| + | *Aus Kausalitätsgründen kann dann natürlich am Ausgang nicht schon für Zeiten $t< 0$ ein Signal auftreten: | ||
| + | :$$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | ||
t<0 \hspace{0.05cm}.$$ | t<0 \hspace{0.05cm}.$$ | ||
| − | + | *Formal lässt sich dies folgendermaßen zeigen: Die Hochpass–Übertragungsfunktion $H_1(f)$ kann wie folgt umgeformt werden: | |
| − | Formal lässt sich dies folgendermaßen zeigen: Die Hochpass–Übertragungsfunktion $H_1(f)$ kann wie folgt umgeformt werden: | + | :$$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} |
| − | $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} | ||
= 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} | = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | *Die zweite Übertragungsfunktion beschreibt die zu $H_1(f)$ äquivalente Tiefpassfunktion, die im Zeitbereich zur Exponentialfunktion führt. | ||
| + | *Die „$1$” wird zu einer Diracfunktion. Mit $T = 2\pi \cdot f_{\rm G}$ gilt somit für $t \ge 0$: | ||
| + | :$$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$ | ||
| + | *Für $t< 0$ gilt dagegen $h_1(t)= 0$, womit die Kausalität nachgewiesen wäre. | ||
| − | |||
| − | |||
| − | |||
| − | |||
'''(3)''' Die Hintereinanderschaltung zweier Hochpässe führt zu folgender Übertragungsfunktion: | '''(3)''' Die Hintereinanderschaltung zweier Hochpässe führt zu folgender Übertragungsfunktion: | ||
| − | $$ | + | :$$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} |
| − | =\frac{\ | + | =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} |
| − | {\ | + | {\big [(1+{\rm j}\cdot f/f_{\rm G}) \cdot (1-{\rm j}\cdot f/f_{\rm G})\big ]^2}= \frac{(f/f_{\rm G})^4 - (f/f_{\rm G})^2 +{\rm j}\cdot 2 |
\cdot (f/f_{\rm G})^3)} | \cdot (f/f_{\rm G})^3)} | ||
| − | {\ | + | {\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$ |
| − | Mit $f = f_{\rm G}$ folgt daraus: | + | *Mit $f = f_{\rm G}$ folgt daraus: |
| − | $$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} | + | :$$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} |
| − | {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} = 0, \hspace{0.4cm} | + | {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} |
{\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$ | {\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' Richtig sind | + | |
| − | * Da für $t < 0$ die Impulsantwort $h_1(t) = 0$ ist, erfüllt auch die Faltungsoperation $h_2(t) = h_1(t) \star h_1(t)$ die Kausalitätsbedingung. Ebenso ergibt die $n$–fache Faltung eine kausale Impulsantwort: $h_n(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | + | '''(4)''' Richtig sind <u>die beiden ersten Lösungsvorschläge</u>: |
| + | * Da für $t < 0$ die Impulsantwort $h_1(t) = 0$ ist, erfüllt auch die Faltungsoperation $h_2(t) = h_1(t) \star h_1(t)$ die Kausalitätsbedingung. | ||
| + | *Ebenso ergibt die $n$–fache Faltung eine kausale Impulsantwort: $h_n(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} | ||
t<0 \hspace{0.05cm}.$ | t<0 \hspace{0.05cm}.$ | ||
| − | *Bei kausaler Impulsantwort $h_2(t)$ hängen aber der Real– und der Imaginärteil der Spektralfunktion $H_2(f)$ über die Hilbert–Transformation zusammen. Mit der Abkürzung $x = f/f_{\rm G}$ | + | *Bei kausaler Impulsantwort $h_2(t)$ hängen aber der Real– und der Imaginärteil der Spektralfunktion $H_2(f)$ über die Hilbert–Transformation zusammen. |
| + | *Mit der Abkürzung $x = f/f_{\rm G}$ und dem Ergebnis der Teilaufgabe '''(3)''' gilt somit: | ||
:$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad | :$$\frac{x^4- x^2}{x^4+2 x^2+1} \quad | ||
\bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad | ||
Aktuelle Version vom 9. Oktober 2021, 15:26 Uhr
Die Grafik zeigt oben den Vierpol mit der Übertragungsfunktion
- $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm},$$
wobei $f_{\rm G}$ die 3dB–Grenzfrequenz angibt:
- $$f_{\rm G} = \frac{R}{2 \pi \cdot L} \hspace{0.05cm}.$$
Durch Hintereinanderschalten von $n$ gleich aufgebauten Vierpolen $H_1(f)$ kommt man zur Übertragungsfunktion
- $$H_n(f) = \big [H_1(f)\big ]^n =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^n}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^n} \hspace{0.05cm}.$$
- Vorausgesetzt ist hierbei eine geeignete Widerstandsentkopplung, die aber zur Lösung dieser Aufgabe nicht von Bedeutung ist.
- Die untere Grafik zeigt zum Beispiel die Realisierung der Übertragungsfunktion $H_2(f)$.
In dieser Aufgabe wird ein solcher Vierpol im Hinblick auf seine Kausalitätseigenschaften betrachtet.
Bei einem jeden kausalen System erfüllen der Real– und der Imaginärteil der Spektralfunktion $H(f)$ die Hilbert–Transformation, was durch das folgende Kurzzeichen ausgedrückt wird:
- $${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm}.$$
Da die Hilbert–Transformation nicht nur für Übertragungsfunktionen, sondern auch für Zeitsignale wichtige Aussagen liefert, wird die Korrespondenz häufig durch die allgemeine Variable $x$ ausgedrückt, die je nach Anwendungsfall als normierte Frequenz oder als normierte Zeit zu interpretieren ist.
Hinweise:
- Die Aufgabe gehört zum Kapitel Folgerungen aus dem Zuordnungssatz.
- Bezug genommen wird auch auf die Therieseiten Hilbert-Transformation sowie Partialbruchzerlegung.
Fragebogen
Musterlösung
- Die angegebene Übertragungsfunktion kann man nach dem Spannungsteilerprinzip berechnen. Es gilt:
- $$H_1(f = 0) = 0, \hspace{0.2cm}H_1(f \rightarrow \infty) = 1.$$
- Es handelt sich um einen Hochpass.
- Für sehr niedrige Frequenzen stellt die Induktivität $L$ einen Kurzschluss dar.
(2) Richtig ist Ja:
- Jedes reale Netzwerk ist kausal. Die Impulsantwort $h(t)$ ist gleich dem Ausgangssignal $y(t)$, wenn zum Zeitpunkt $t= 0$ am Eingang ein extrem kurzfristiger Impuls – ein so genannter Diracimpuls – angelegt wird.
- Aus Kausalitätsgründen kann dann natürlich am Ausgang nicht schon für Zeiten $t< 0$ ein Signal auftreten:
- $$y(t) = h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$$
- Formal lässt sich dies folgendermaßen zeigen: Die Hochpass–Übertragungsfunktion $H_1(f)$ kann wie folgt umgeformt werden:
- $$H_1(f) = \frac{{\rm j}\cdot f/f_{\rm G}}{1+{\rm j}\cdot f/f_{\rm G}} = 1- \frac{1}{1+{\rm j}\cdot f/f_{\rm G}} \hspace{0.05cm}.$$
- Die zweite Übertragungsfunktion beschreibt die zu $H_1(f)$ äquivalente Tiefpassfunktion, die im Zeitbereich zur Exponentialfunktion führt.
- Die „$1$” wird zu einer Diracfunktion. Mit $T = 2\pi \cdot f_{\rm G}$ gilt somit für $t \ge 0$:
- $$h_1(t) = \delta(t) - {1}/{T} \cdot {\rm e}^{-t/T} \hspace{0.05cm}.$$
- Für $t< 0$ gilt dagegen $h_1(t)= 0$, womit die Kausalität nachgewiesen wäre.
(3) Die Hintereinanderschaltung zweier Hochpässe führt zu folgender Übertragungsfunktion:
- $$H_2(f) = \big [H_1(f)\big ]^2 =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2}{\big [1+{\rm j}\cdot f/f_{\rm G}\big ]^2} =\frac{\big [{\rm j}\cdot f/f_{\rm G}\big ]^2 \cdot \big [(1-{\rm j}\cdot f/f_{\rm G})\big ]^2} {\big [(1+{\rm j}\cdot f/f_{\rm G}) \cdot (1-{\rm j}\cdot f/f_{\rm G})\big ]^2}= \frac{(f/f_{\rm G})^4 - (f/f_{\rm G})^2 +{\rm j}\cdot 2 \cdot (f/f_{\rm G})^3)} {\big [1+(f/f_{\rm G})^2 \big ]^2}\hspace{0.05cm}.$$
- Mit $f = f_{\rm G}$ folgt daraus:
- $$H_2(f = f_{\rm G}) = \frac{1 - 1 +{\rm j}\cdot 2} {4}= {\rm j} /{2} \hspace{0.5cm}\Rightarrow \hspace{0.5cm}{\rm Re} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0}, \hspace{0.4cm} {\rm Im} \left\{ H_2(f = f_{\rm G}) \right \} \hspace{0.15cm}\underline{ = 0.5}\hspace{0.05cm}.$$
(4) Richtig sind die beiden ersten Lösungsvorschläge:
- Da für $t < 0$ die Impulsantwort $h_1(t) = 0$ ist, erfüllt auch die Faltungsoperation $h_2(t) = h_1(t) \star h_1(t)$ die Kausalitätsbedingung.
- Ebenso ergibt die $n$–fache Faltung eine kausale Impulsantwort: $h_n(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}.$
- Bei kausaler Impulsantwort $h_2(t)$ hängen aber der Real– und der Imaginärteil der Spektralfunktion $H_2(f)$ über die Hilbert–Transformation zusammen.
- Mit der Abkürzung $x = f/f_{\rm G}$ und dem Ergebnis der Teilaufgabe (3) gilt somit:
- $$\frac{x^4- x^2}{x^4+2 x^2+1} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{2x^3}{x^4+2 x^2+1}\hspace{0.05cm}.$$