Aufgaben:Aufgabe 3.11Z: Extrem unsymmetrischer Kanal: Unterschied zwischen den Versionen
Aus LNTwww
K (Guenter verschob die Seite 3.11Z Extrem unsymmetrischer Kanal nach Aufgabe 3.11Z: Extrem unsymmetrischer Kanal) |
|||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID2800__Inf_Z_3_10.png|right|frame|Einseitig verfälschender Kanal]] | [[Datei:P_ID2800__Inf_Z_3_10.png|right|frame|Einseitig verfälschender Kanal]] | ||
Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften: | Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften: | ||
| − | * Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$. | + | * Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$. |
| − | * Das Symbol $X = 1$ wird maximal verfälscht. Aus Sicht der Informationstheorie bedeutet dies: | + | * Das Symbol $X = 1$ wird maximal verfälscht. |
| − | :$${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}$$ | + | |
| + | |||
| + | Aus Sicht der Informationstheorie bedeutet dies: | ||
| + | :$${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}.$$ | ||
Zu bestimmen sind in dieser Aufgabe: | Zu bestimmen sind in dieser Aufgabe: | ||
| − | * die Transinformation $I(X; Y)$ für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. Es gilt allgemein: | + | * die Transinformation $I(X; Y)$ für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. <br>Es gilt allgemein: |
| − | :$$ I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}=H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm} =\hspace{ | + | :$$ I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}=\hspace{0.05cm}H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm} =\hspace{0.05cm} H(X) + H(Y)- H(XY)\hspace{0.05cm},$$ |
* die Kanalkapazität: | * die Kanalkapazität: | ||
| − | :$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ | + | :$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$ |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung|Anwendung auf die Digitalsignalübertragung]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Kanalkapazit.C3.A4t_eines_Bin.C3.A4rkanals|Kanalkapazität eines Binärkanals]]. | + | *Bezug genommen wird insbesondere auf die Seite [[Informationstheorie/Anwendung_auf_die_Digitalsignalübertragung#Kanalkapazit.C3.A4t_eines_Bin.C3.A4rkanals|Kanalkapazität eines Binärkanals]]. |
| − | *In der [[Aufgaben:3.14_Kanalcodierungstheorem|Aufgabe 3.14]] sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden. | + | *In der [[Aufgaben:3.14_Kanalcodierungstheorem|Aufgabe 3.14]] sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden. |
| − | + | ||
| Zeile 25: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie die Quellenentropie allgemein und für $p_0 = 0.4$. | + | {Berechnen Sie die Quellenentropie allgemein und für $\underline{p_0 = 0.4}$. |
|type="{}"} | |type="{}"} | ||
$H(X) \ = \ $ { 0.971 3% } $\ \rm bit$ | $H(X) \ = \ $ { 0.971 3% } $\ \rm bit$ | ||
| − | {Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4$. | + | {Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4$. |
|type="{}"} | |type="{}"} | ||
$H(Y) \ = \ $ { 0.881 3% } $\ \rm bit$ | $H(Y) \ = \ $ { 0.881 3% } $\ \rm bit$ | ||
| − | {Berechnen Sie die Verbundentropie allgemein und für $p_0 = 0.4$. | + | {Berechnen Sie die Verbundentropie allgemein und für $p_0 = 0.4$. |
|type="{}"} | |type="{}"} | ||
$H(XY) \ = \ $ { 1.571 3% } $\ \rm bit$ | $H(XY) \ = \ $ { 1.571 3% } $\ \rm bit$ | ||
| − | {Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4$. | + | {Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4$. |
|type="{}"} | |type="{}"} | ||
$I(X; Y) \ = \ $ { 0.281 3% } $\ \rm bit$ | $I(X; Y) \ = \ $ { 0.281 3% } $\ \rm bit$ | ||
| − | {Welche Wahrscheinlichkeit $p_0^{(*)}$ führt zur Kanalkapazität $C$? | + | {Welche Wahrscheinlichkeit $p_0^{(*)}$ führt zur Kanalkapazität $C$? |
|type="{}"} | |type="{}"} | ||
$p_0^{(*)} \ = \ $ { 0.6 3% } | $p_0^{(*)} \ = \ $ { 0.6 3% } | ||
| Zeile 49: | Zeile 59: | ||
$C \ = \ $ { 0.322 3% } $\ \rm bit$ | $C \ = \ $ { 0.322 3% } $\ \rm bit$ | ||
| − | {Wie groß sind die bedingten Entropien mit $p_0 = p_0^{(*)}$ gemäß Teilaufgabe (5)? | + | {Wie groß sind die bedingten Entropien mit $p_0 = p_0^{(*)}$ gemäß Teilaufgabe '''(5)'''? |
|type="{}"} | |type="{}"} | ||
$H(X|Y) \ = \ $ { 0.649 3% } $\ \rm bit$ | $H(X|Y) \ = \ $ { 0.649 3% } $\ \rm bit$ | ||
| Zeile 60: | Zeile 70: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Die Quellenentropie ergibt sich entsprechend der binären Entropiefunktion: | '''(1)''' Die Quellenentropie ergibt sich entsprechend der binären Entropiefunktion: | ||
| − | :$$H(X) = H_{\rm bin}(p_0)= H_{\rm bin}(0.4) \hspace{0.15cm} \underline {=0.971\,{\rm bit}} \hspace{0.05cm}$$ | + | :$$H(X) = H_{\rm bin}(p_0)= H_{\rm bin}(0.4) \hspace{0.15cm} \underline {=0.971\,{\rm bit}} \hspace{0.05cm}.$$ |
| + | |||
| + | |||
'''(2)''' Die Wahrscheinlichkeiten der Sinkensymbole sind: | '''(2)''' Die Wahrscheinlichkeiten der Sinkensymbole sind: | ||
:$$P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.3\hspace{0.05cm},\hspace{0.2cm} P_Y(0) = 1-P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.7$$ | :$$P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.3\hspace{0.05cm},\hspace{0.2cm} P_Y(0) = 1-P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.7$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm} H(Y) = H_{\rm bin}(\frac{1+p_0}{2})= H_{\rm bin}(0.7) \hspace{0.15cm} \underline {=0.881\,{\rm bit}} \hspace{0.05cm}$$ | + | :$$\Rightarrow \hspace{0.3cm} H(Y) = H_{\rm bin}(\frac{1+p_0}{2})= H_{\rm bin}(0.7) \hspace{0.15cm} \underline {=0.881\,{\rm bit}} \hspace{0.05cm}.$$ |
| + | |||
| − | '''(3)''' Die Verbundwahrscheinlichkeiten $p_{μκ} = {\rm Pr}[(X = μ) ∩ (Y = κ)]$ ergeben sich zu: | + | |
| + | '''(3)''' Die Verbundwahrscheinlichkeiten $p_{μκ} = {\rm Pr}\big[(X = μ) ∩ (Y = κ)\big] $ ergeben sich zu: | ||
:$$ p_{00} = p_0 \hspace{0.05cm},\hspace{0.3cm} p_{01} = 0 \hspace{0.05cm},\hspace{0.3cm} p_{10} = (1 - p_0)/2 \hspace{0.05cm},\hspace{0.3cm} p_{11} = (1 - p_0)/2$$ | :$$ p_{00} = p_0 \hspace{0.05cm},\hspace{0.3cm} p_{01} = 0 \hspace{0.05cm},\hspace{0.3cm} p_{10} = (1 - p_0)/2 \hspace{0.05cm},\hspace{0.3cm} p_{11} = (1 - p_0)/2$$ | ||
:$$\Rightarrow \hspace{0.3cm} H(XY) =p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + 2 \cdot \frac{1-p_0}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{ 1- p_0} = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ 1- p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} (2)$$ | :$$\Rightarrow \hspace{0.3cm} H(XY) =p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + 2 \cdot \frac{1-p_0}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{ 1- p_0} = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ 1- p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} (2)$$ | ||
| − | :$$\Rightarrow \hspace{0.3cm}H(XY) =H_{\rm bin}(p_0) + 1 - p_0 \hspace{0.05cm}$$ | + | :$$\Rightarrow \hspace{0.3cm}H(XY) =H_{\rm bin}(p_0) + 1 - p_0 \hspace{0.05cm}.$$ |
| − | Das numerische Ergebnis für $p_0 = 0.4$ lautet somit: | + | *Das numerische Ergebnis für $p_0 = 0.4$ lautet somit: |
| − | :$$H(XY) = H_{\rm bin}(0.4) + 0.6 = 0.971 + 0.6 \hspace{0.15cm} \underline {=1.571\,{\rm bit}} \hspace{0.05cm}$$ | + | :$$H(XY) = H_{\rm bin}(0.4) + 0.6 = 0.971 + 0.6 \hspace{0.15cm} \underline {=1.571\,{\rm bit}} \hspace{0.05cm}.$$ |
| + | |||
| + | |||
'''(4)''' Eine (mögliche) Gleichung zur Berechnung der Transinformation lautet: | '''(4)''' Eine (mögliche) Gleichung zur Berechnung der Transinformation lautet: | ||
| − | :$$ I(X;Y) = H(X) + H(Y)- H(XY)\hspace{0.05cm}$$ | + | :$$ I(X;Y) = H(X) + H(Y)- H(XY)\hspace{0.05cm}.$$ |
| − | Daraus erhält man mit den Ergebnissen der ersten drei Teilaufgaben: | + | *Daraus erhält man mit den Ergebnissen der ersten drei Teilaufgaben: |
| − | :$$I(X;Y) = H_{\rm bin}(p_0) + H_{\rm bin}(\frac{1+p_0}{2}) - H_{\rm bin}(p_0) -1 + p_0 = H_{\rm bin}(\frac{1+p_0}{2}) -1 + p_0$$ | + | :$$I(X;Y) = H_{\rm bin}(p_0) + H_{\rm bin}(\frac{1+p_0}{2}) - H_{\rm bin}(p_0) -1 + p_0 = H_{\rm bin}(\frac{1+p_0}{2}) -1 + p_0.$$ |
| − | :$$ \Rightarrow \hspace{0.3cm} p_0 = 0.4 {\rm :}\hspace{0.5cm} I(X;Y) = H_{\rm bin}(0.7) - 0.6 = 0.881 - 0.6 \hspace{0.15cm} \underline {=0.281\,{\rm bit}}\hspace{0.05cm}$$ | + | :$$ \Rightarrow \hspace{0.3cm} p_0 = 0.4 {\rm :}\hspace{0.5cm} I(X;Y) = H_{\rm bin}(0.7) - 0.6 = 0.881 - 0.6 \hspace{0.15cm} \underline {=0.281\,{\rm bit}}\hspace{0.05cm}.$$ |
| − | '''(5)''' Die Kanalkapazität $C$ ist die Transinformation $I(X; Y) $bei bestmöglichen Wahrscheinlichkeiten $p_0$ und $p_1$ der Quellensymbole. Nach Differentiation erhält man die Bestimmungsgleichung: | + | |
| + | |||
| + | '''(5)''' Die Kanalkapazität $C$ ist die Transinformation $I(X; Y)$ bei bestmöglichen Wahrscheinlichkeiten $p_0$ und $p_1$ der Quellensymbole. | ||
| + | *Nach Differentiation erhält man die Bestimmungsgleichung: | ||
:$$\frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} I(X;Y) = | :$$\frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} I(X;Y) = | ||
\frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} H_{\rm bin}(\frac{1+p_0}{2}) +1 \stackrel{!}{=} 0 | \frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} H_{\rm bin}(\frac{1+p_0}{2}) +1 \stackrel{!}{=} 0 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Mit dem Differentialquotienten der binären Entropiefunktion | + | *Mit dem Differentialquotienten der binären Entropiefunktion |
:$$ \frac{\rm d}{{\rm d}p} \hspace{0.1cm} H_{\rm bin}(p) = {\rm log}_2 \hspace{0.1cm} \frac{1-p}{ p} \hspace{0.05cm},$$ | :$$ \frac{\rm d}{{\rm d}p} \hspace{0.1cm} H_{\rm bin}(p) = {\rm log}_2 \hspace{0.1cm} \frac{1-p}{ p} \hspace{0.05cm},$$ | ||
| − | und entsprechendes Nachdifferenzieren erhält man : | + | :und entsprechendes Nachdifferenzieren erhält man: |
:$${1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{1- (1-p_0)/2} +1 \stackrel{!}{=} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{(1+p_0)/2} +1 \stackrel{!}{=} 0$$ | :$${1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{1- (1-p_0)/2} +1 \stackrel{!}{=} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{(1+p_0)/2} +1 \stackrel{!}{=} 0$$ | ||
| − | :$$ \Rightarrow \hspace{0.3cm} {\rm log}_2 \hspace{0.1cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_0 \hspace{0.15cm} \underline {=0.6}\hspace{0.05cm}.$$ | + | :$$ \Rightarrow \hspace{0.3cm} {\rm log}_2 \hspace{0.1cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_0 \hspace{0.15cm} \underline {=0.6}=p_0^{(*)}\hspace{0.05cm}.$$ |
| + | |||
| + | |||
'''(6)''' Für die Kanalkapazität gilt dementsprechend: | '''(6)''' Für die Kanalkapazität gilt dementsprechend: | ||
:$$C = I(X;Y) \big |_{p_0 \hspace{0.05cm}=\hspace{0.05cm} 0.6} = H_{\rm bin}(0.8) - 0.4 = 0.722 -0.4 \hspace{0.15cm} \underline {=0.322\,{\rm bit}}\hspace{0.05cm}.$$ | :$$C = I(X;Y) \big |_{p_0 \hspace{0.05cm}=\hspace{0.05cm} 0.6} = H_{\rm bin}(0.8) - 0.4 = 0.722 -0.4 \hspace{0.15cm} \underline {=0.322\,{\rm bit}}\hspace{0.05cm}.$$ | ||
| − | In der Aufgabe A3.14 wird dieses Ergebnis im Vergleich zum BSC–Kanalmodell interpretiert. | + | *In der Aufgabe A3.14 wird dieses Ergebnis im Vergleich zum BSC–Kanalmodell interpretiert. |
| + | |||
| + | |||
| + | |||
'''(7)''' Für die Äquivokation gilt: | '''(7)''' Für die Äquivokation gilt: | ||
| − | :$$ H(X \hspace{-0.1cm}\mid \hspace{-0.1cm}Y) = H(X) - I(X;Y) = 0.971 -0.322 \hspace{0.15cm} \underline {=0.649\,{\rm bit}}\hspace{0.05cm}$$ | + | :$$ H(X \hspace{-0.1cm}\mid \hspace{-0.1cm}Y) = H(X) - I(X;Y) = 0.971 -0.322 \hspace{0.15cm} \underline {=0.649\,{\rm bit}}\hspace{0.05cm}.$$ |
| − | Wegen $H_{\rm bin}(0.4) = H_{\rm bin}(0.6)$ ergibt sich die gleiche Quellenentropie $H(X)$ wie in Teilaufgabe (1). Die Sinkenentropie muss neu berechnet werden. Mit $p_0 = 0.6$ erhält man $H(Y) = H_{\rm bin}(0.8) = 0.722\ \rm bit$ | + | *Wegen $H_{\rm bin}(0.4) = H_{\rm bin}(0.6)$ ergibt sich die gleiche Quellenentropie $H(X)$ wie in Teilaufgabe '''(1)'''. |
| − | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) - I(X;Y) = 0.722 -0.322 \hspace{0.15cm} \underline {=0.400\,{\rm bit}}\hspace{0.05cm}$$ | + | *Die Sinkenentropie muss neu berechnet werden. Mit $p_0 = 0.6$ erhält man $H(Y) = H_{\rm bin}(0.8) = 0.722\ \rm bit$. |
| + | * Damit ergibt sich für die Irrelevanz: | ||
| + | :$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) - I(X;Y) = 0.722 -0.322 \hspace{0.15cm} \underline {=0.400\,{\rm bit}}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 22. September 2021, 13:04 Uhr
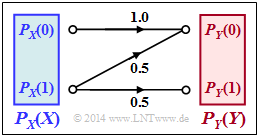
Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften:
- Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$.
- Das Symbol $X = 1$ wird maximal verfälscht.
Aus Sicht der Informationstheorie bedeutet dies:
- $${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}.$$
Zu bestimmen sind in dieser Aufgabe:
- die Transinformation $I(X; Y)$ für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$.
Es gilt allgemein:
- $$ I(X;Y) = H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}=\hspace{0.05cm}H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm} =\hspace{0.05cm} H(X) + H(Y)- H(XY)\hspace{0.05cm},$$
- die Kanalkapazität:
- $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Anwendung auf die Digitalsignalübertragung.
- Bezug genommen wird insbesondere auf die Seite Kanalkapazität eines Binärkanals.
- In der Aufgabe 3.14 sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden.
Fragebogen
Musterlösung
(1) Die Quellenentropie ergibt sich entsprechend der binären Entropiefunktion:
- $$H(X) = H_{\rm bin}(p_0)= H_{\rm bin}(0.4) \hspace{0.15cm} \underline {=0.971\,{\rm bit}} \hspace{0.05cm}.$$
(2) Die Wahrscheinlichkeiten der Sinkensymbole sind:
- $$P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.3\hspace{0.05cm},\hspace{0.2cm} P_Y(0) = 1-P_Y(1) = p_1/2 = (1 - p_0)/2 = 0.7$$
- $$\Rightarrow \hspace{0.3cm} H(Y) = H_{\rm bin}(\frac{1+p_0}{2})= H_{\rm bin}(0.7) \hspace{0.15cm} \underline {=0.881\,{\rm bit}} \hspace{0.05cm}.$$
(3) Die Verbundwahrscheinlichkeiten $p_{μκ} = {\rm Pr}\big[(X = μ) ∩ (Y = κ)\big] $ ergeben sich zu:
- $$ p_{00} = p_0 \hspace{0.05cm},\hspace{0.3cm} p_{01} = 0 \hspace{0.05cm},\hspace{0.3cm} p_{10} = (1 - p_0)/2 \hspace{0.05cm},\hspace{0.3cm} p_{11} = (1 - p_0)/2$$
- $$\Rightarrow \hspace{0.3cm} H(XY) =p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + 2 \cdot \frac{1-p_0}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{ 1- p_0} = p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ 1- p_0} + (1-p_0) \cdot {\rm log}_2 \hspace{0.1cm} (2)$$
- $$\Rightarrow \hspace{0.3cm}H(XY) =H_{\rm bin}(p_0) + 1 - p_0 \hspace{0.05cm}.$$
- Das numerische Ergebnis für $p_0 = 0.4$ lautet somit:
- $$H(XY) = H_{\rm bin}(0.4) + 0.6 = 0.971 + 0.6 \hspace{0.15cm} \underline {=1.571\,{\rm bit}} \hspace{0.05cm}.$$
(4) Eine (mögliche) Gleichung zur Berechnung der Transinformation lautet:
- $$ I(X;Y) = H(X) + H(Y)- H(XY)\hspace{0.05cm}.$$
- Daraus erhält man mit den Ergebnissen der ersten drei Teilaufgaben:
- $$I(X;Y) = H_{\rm bin}(p_0) + H_{\rm bin}(\frac{1+p_0}{2}) - H_{\rm bin}(p_0) -1 + p_0 = H_{\rm bin}(\frac{1+p_0}{2}) -1 + p_0.$$
- $$ \Rightarrow \hspace{0.3cm} p_0 = 0.4 {\rm :}\hspace{0.5cm} I(X;Y) = H_{\rm bin}(0.7) - 0.6 = 0.881 - 0.6 \hspace{0.15cm} \underline {=0.281\,{\rm bit}}\hspace{0.05cm}.$$
(5) Die Kanalkapazität $C$ ist die Transinformation $I(X; Y)$ bei bestmöglichen Wahrscheinlichkeiten $p_0$ und $p_1$ der Quellensymbole.
- Nach Differentiation erhält man die Bestimmungsgleichung:
- $$\frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} I(X;Y) = \frac{\rm d}{{\rm d}p_0} \hspace{0.1cm} H_{\rm bin}(\frac{1+p_0}{2}) +1 \stackrel{!}{=} 0 \hspace{0.05cm}.$$
- Mit dem Differentialquotienten der binären Entropiefunktion
- $$ \frac{\rm d}{{\rm d}p} \hspace{0.1cm} H_{\rm bin}(p) = {\rm log}_2 \hspace{0.1cm} \frac{1-p}{ p} \hspace{0.05cm},$$
- und entsprechendes Nachdifferenzieren erhält man:
- $${1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{1- (1-p_0)/2} +1 \stackrel{!}{=} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{(1-p_0)/2}{(1+p_0)/2} +1 \stackrel{!}{=} 0$$
- $$ \Rightarrow \hspace{0.3cm} {\rm log}_2 \hspace{0.1cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac{1+p_0}{1-p_0} \stackrel{!}{=} 4 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_0 \hspace{0.15cm} \underline {=0.6}=p_0^{(*)}\hspace{0.05cm}.$$
(6) Für die Kanalkapazität gilt dementsprechend:
- $$C = I(X;Y) \big |_{p_0 \hspace{0.05cm}=\hspace{0.05cm} 0.6} = H_{\rm bin}(0.8) - 0.4 = 0.722 -0.4 \hspace{0.15cm} \underline {=0.322\,{\rm bit}}\hspace{0.05cm}.$$
- In der Aufgabe A3.14 wird dieses Ergebnis im Vergleich zum BSC–Kanalmodell interpretiert.
(7) Für die Äquivokation gilt:
- $$ H(X \hspace{-0.1cm}\mid \hspace{-0.1cm}Y) = H(X) - I(X;Y) = 0.971 -0.322 \hspace{0.15cm} \underline {=0.649\,{\rm bit}}\hspace{0.05cm}.$$
- Wegen $H_{\rm bin}(0.4) = H_{\rm bin}(0.6)$ ergibt sich die gleiche Quellenentropie $H(X)$ wie in Teilaufgabe (1).
- Die Sinkenentropie muss neu berechnet werden. Mit $p_0 = 0.6$ erhält man $H(Y) = H_{\rm bin}(0.8) = 0.722\ \rm bit$.
- Damit ergibt sich für die Irrelevanz:
- $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(Y) - I(X;Y) = 0.722 -0.322 \hspace{0.15cm} \underline {=0.400\,{\rm bit}}\hspace{0.05cm}.$$