Aufgaben:Aufgabe 4.2Z: Gemischte Zufallsgrößen: Unterschied zwischen den Versionen
K (Guenter verschob die Seite 4.2Z Gemischte Zufallsgrößen nach Aufgabe 4.2Z: Gemischte Zufallsgrößen) |
|||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
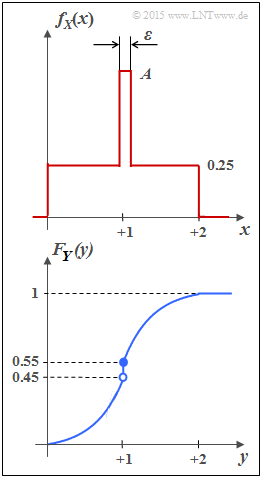
| − | [[Datei:P_ID2868__Inf_Z_4_2_neu.png|right|frame|WDF von | + | [[Datei:P_ID2868__Inf_Z_4_2_neu.png|right|frame|WDF von $X$ (oben), und <br>VTF von $Y$ (unten)]] |
| − | Man spricht von einer | + | Man spricht von einer „gemischten Zufallsgröße”, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet. |
| − | *Die Zufallsgröße $Y$ mit der [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] $F_Y(y)$ gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil. | + | *Die Zufallsgröße $Y$ mit der [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] $F_Y(y)$ gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil. |
| − | *Die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion]] $f_Y(y)$ erhält man aus $F_Y(y)$ durch Differentiation. | + | *Die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion]] $f_Y(y)$ erhält man aus $F_Y(y)$ durch Differentiation. |
| − | *Aus dem Sprung bei $y= 1$ in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF). | + | *Aus dem Sprung bei $y= 1$ in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF). |
| − | *In der Teilaufgabe | + | *In der Teilaufgabe '''(4)''' soll die differentielle Entropie $h(Y)$ der Zufallsgröße $Y$ ermittelt werden (in bit), wobei von folgender Gleichung auszugehen ist: |
:$$h(Y) = | :$$h(Y) = | ||
| − | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_Y(y) ] \hspace{0.1cm}{\rm d}y | + | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *In der Teilaufgabe | + | *In der Teilaufgabe '''(2)''' ist die differentielle Entropie $h(X)$ der Zufallsgröße $X$ zu berechnen, deren WDF $f_X(x)$ oben skizziert ist. Führt man einen geeigneten Grenzübergang durch, so wird auch aus der Zufallsgröße $X$ eine gemischte Zufallsgröße. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Differentielle_Entropie|Differentielle Entropie]]. | + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Differentielle_Entropie|Differentielle Entropie]]. |
| − | *Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] des Buches „Stochastische Signaltheorie”. | + | *Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel [[Stochastische_Signaltheorie/Verteilungsfunktion|Verteilungsfunktion]] des Buches „Stochastische Signaltheorie”. |
| − | + | ||
| Zeile 28: | Zeile 34: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die WDF–Höhe $A$ von $f_X(x)$ um $x = 1$? | + | {Wie groß ist die WDF–Höhe $A$ von $f_X(x)$ um $x = 1$? |
|type="[]"} | |type="[]"} | ||
- $A = 0.5/\varepsilon$, | - $A = 0.5/\varepsilon$, | ||
| Zeile 34: | Zeile 40: | ||
- $A = 1/\varepsilon$. | - $A = 1/\varepsilon$. | ||
| − | {Berechnen Sie die differentielle Entropie für verschiedene $\varepsilon$–Werte. | + | {Berechnen Sie die differentielle Entropie für verschiedene $\varepsilon$–Werte. |
|type="{}"} | |type="{}"} | ||
$ε = 10^{-1}\text{:} \ \ h(X) \ = \ $ { 0.644 3% } $\ \rm bit$ | $ε = 10^{-1}\text{:} \ \ h(X) \ = \ $ { 0.644 3% } $\ \rm bit$ | ||
| Zeile 40: | Zeile 46: | ||
$ε = 10^{-3}\text{:} \ \ h(X) \ = \ $ { -7.2--6.8 } $\ \rm bit$ | $ε = 10^{-3}\text{:} \ \ h(X) \ = \ $ { -7.2--6.8 } $\ \rm bit$ | ||
| − | {Welches Ergebnis liefert der Grenzwert $ε \to 0$? | + | {Welches Ergebnis liefert der Grenzwert $ε \to 0$? |
|type="[]"} | |type="[]"} | ||
| − | + $f_X(x)$ hat nun einen kontinuierlichen und einen diskreten Anteil. | + | + $f_X(x)$ hat nun einen kontinuierlichen und einen diskreten Anteil. |
| − | + Die differentielle Energie $h(X)$ ist negativ. | + | + Die differentielle Energie $h(X)$ ist negativ. |
| − | + Der Betrag $|h(X)|$ ist unendlich groß. | + | + Der Betrag $|h(X)|$ ist unendlich groß. |
| − | {Welche Aussagen treffen für die Zufallsgröße $Y$ zu? | + | {Welche Aussagen treffen für die Zufallsgröße $Y$ zu? |
|type="[]"} | |type="[]"} | ||
| − | - Der VTF–Wert an der Stelle $y = 1$ ist $0.5$. | + | - Der VTF–Wert an der Stelle $y = 1$ ist $0.5$. |
| − | + $Y$ beinhaltet einen diskreten und einen kontinuierlichen Anteil | + | + $Y$ beinhaltet einen diskreten und einen kontinuierlichen Anteil. |
| − | + Der diskrete Anteil bei $Y = 1$ | + | + Der diskrete Anteil bei $Y = 1$ tritt mit $10\%$ Wahrscheinlichkeit auf. |
| − | - Der kontinuierliche Anteil von $Y$ ist gleichverteilt. | + | - Der kontinuierliche Anteil von $Y$ ist gleichverteilt. |
| − | + Die differentiellen Entropien von $X$ und $Y$ sind gleich. | + | + Die differentiellen Entropien von $X$ und $Y$ sind gleich. |
| Zeile 61: | Zeile 67: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>, weil das Integral über die WDF $1$ ergeben muss: | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>, weil das Integral über die WDF $1$ ergeben muss: |
:$$f_X(x) \hspace{0.1cm}{\rm d}x = | :$$f_X(x) \hspace{0.1cm}{\rm d}x = | ||
0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1 \hspace{0.3cm} | 0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1 \hspace{0.3cm} | ||
\Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 | \Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$$ | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
'''(2)''' Die differentielle Entropie (in „bit”) ist wie folgt gegeben: | '''(2)''' Die differentielle Entropie (in „bit”) ist wie folgt gegeben: | ||
| Zeile 75: | Zeile 83: | ||
\hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + | \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + | ||
\hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x | \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x | ||
| − | + \hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} [0.5/\varepsilon + 0.25] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$ | + | + \hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} \big [0.5/\varepsilon + 0.25 \big ] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$ |
:$$ \Rightarrow \hspace{0.3cm} h(X) = 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) | :$$ \Rightarrow \hspace{0.3cm} h(X) = 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Insbesondere erhält man | Insbesondere erhält man | ||
| − | * für $\varepsilon = 0.1$: | + | * für $\varepsilon = 0.1$: |
:$$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 | :$$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 | ||
\hspace{0.15cm}\underline{= 0.644\,{\rm bit}} | \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * für $\varepsilon = 0.01$: | + | * für $\varepsilon = 0.01$: |
:$$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 | :$$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 | ||
\hspace{0.15cm}\underline{= -0.850\,{\rm bit}} | \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | * für $\varepsilon = 0.001$: | + | * für $\varepsilon = 0.001$: |
:$$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 | :$$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 | ||
\hspace{0.15cm}\underline{= -6.968\,{\rm bit}} | \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' <u>Alle Lösungsvorschläge</u> sind | + | |
| − | *Nach dem Grenzübergang | + | '''(3)''' <u>Alle Lösungsvorschläge</u> sind zutreffend: |
| − | :$$h(X) = \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)] | + | *Nach dem Grenzübergang $\varepsilon → 0$ erhält man für die differentielle Entropie |
| + | :$$h(X) = \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}\big[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)\big] | ||
= 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) | = 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
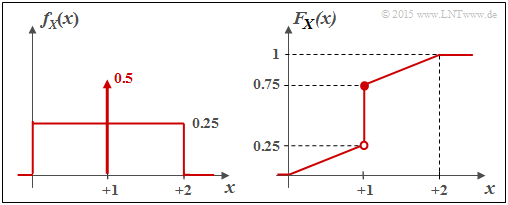
| + | [[Datei:P_ID2871__Inf_Z_4_2c_neu.png|right|frame|WDF und VTF der gemischten Zufallsgröße $X$]] | ||
*Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu | *Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu | ||
:$$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} | :$$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Es handelt sich demzufolge um eine „gemischte” Zufallsgröße mit | Es handelt sich demzufolge um eine „gemischte” Zufallsgröße mit | ||
| − | * einem stochastischen, gleichverteilten Anteil im Bereich $0 \le x \le 2$, und | + | * einem stochastischen, gleichverteilten Anteil im Bereich $0 \le x \le 2$, und |
| − | * einem diskreten Anteil bei $x = 1$ mit der Wahrscheinlichkeit $0.5$. | + | * einem diskreten Anteil bei $x = 1$ mit der Wahrscheinlichkeit $0.5$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Richtig ist auch der letzte Vorschlag: $h(Y) = h(X) = - \infty$. | + | Die Grafik zeigt links die WDF $f_X(x)$ und rechts die Verteilungsfunktion $F_X(x)$. |
| − | <br>Denn: Bei jeder Zufallsgröße mit einem diskreten Anteil – und ist er auch noch so klein, ist die differentielle Entropie gleich minus unendlich. | + | <br clear=all> |
| + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 2, 3 und 5</u>. | ||
| + | Die untere Grafik zeigt die WDF und die VTF der Zufallsgröße $Y$. Man erkennt: | ||
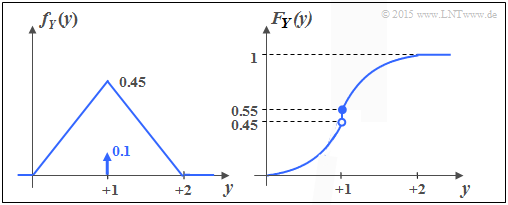
| + | [[Datei:P_ID2872__Inf_Z_4_2d_neu.png|right|frame|WDF und VTF der gemischten Zufallsgröße $Y$]] | ||
| + | * $Y$ beinhaltet wie $X$ einen kontinuierlichen und einen diskreten Anteil. | ||
| + | * Der diskrete Anteil tritt mit der Wahrscheinlichkeit ${\rm Pr}(Y = 1) = 0.1$ auf. | ||
| + | * Da $F_Y(y)= {\rm Pr}(Y \le y)$ gilt, ergibt sich der rechtsseitige Grenzwert: | ||
| + | :$$F_Y(y = 1) = 0.55.$$ | ||
| + | * Der kontinuierliche Anteil ist nicht gleichverteilt; vielmehr liegt eine Dreieckverteilung vor. | ||
| + | *Richtig ist auch der letzte Vorschlag: $h(Y) = h(X) = - \infty$. | ||
| + | <br clear=all> | ||
| + | Denn: '''Bei jeder Zufallsgröße mit einem diskreten Anteil – und ist er auch noch so klein, ist die differentielle Entropie gleich minus unendlich'''. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 10. Februar 2020, 17:38 Uhr
Man spricht von einer „gemischten Zufallsgröße”, wenn die Zufallsgröße neben einem kontinuierlichen Anteil auch noch diskrete Anteile beinhaltet.
- Die Zufallsgröße $Y$ mit der Verteilungsfunktion $F_Y(y)$ gemäß der unteren Skizze besitzt beispielsweise sowohl einen kontinuierlichen als auch einen diskreten Anteil.
- Die Wahrscheinlichkeitsdichtefunktion $f_Y(y)$ erhält man aus $F_Y(y)$ durch Differentiation.
- Aus dem Sprung bei $y= 1$ in der Verteilungsfunktion (VTF) wird somit ein „Dirac” in der Wahrscheinlichkeitsdichtefunktion (WDF).
- In der Teilaufgabe (4) soll die differentielle Entropie $h(Y)$ der Zufallsgröße $Y$ ermittelt werden (in bit), wobei von folgender Gleichung auszugehen ist:
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log}_2 \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
- In der Teilaufgabe (2) ist die differentielle Entropie $h(X)$ der Zufallsgröße $X$ zu berechnen, deren WDF $f_X(x)$ oben skizziert ist. Führt man einen geeigneten Grenzübergang durch, so wird auch aus der Zufallsgröße $X$ eine gemischte Zufallsgröße.
Hinweise:
- Die Aufgabe gehört zum Kapitel Differentielle Entropie.
- Weitere Informationen zu gemischten Zufallsgrößen finden Sie im Kapitel Verteilungsfunktion des Buches „Stochastische Signaltheorie”.
Fragebogen
Musterlösung
- $$f_X(x) \hspace{0.1cm}{\rm d}x = 0.25 \cdot 2 + (A - 0.25) \cdot \varepsilon \stackrel{!}{=} 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}(A - 0.25) \cdot \varepsilon \stackrel{!}{=} 0.5 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.5/\varepsilon +0.25\hspace{0.05cm}.$$
(2) Die differentielle Entropie (in „bit”) ist wie folgt gegeben:
- $$h(X) = \hspace{0.1cm} \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{f_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Wir unterteilen nun das Integral in drei Teilintegrale:
- $$h(X) = \hspace{-0.25cm} \int\limits_{0}^{1-\varepsilon/2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1+\varepsilon/2}^{2} \hspace{-0.15cm} 0.25 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.25} \hspace{0.1cm}{\rm d}x + \hspace{-0.25cm}\int\limits_{1-\varepsilon/2}^{1+\varepsilon/2} \hspace{-0.15cm} \big [0.5/\varepsilon + 0.25 \big ] \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5/\varepsilon + 0.25} \hspace{0.1cm}{\rm d}x $$
- $$ \Rightarrow \hspace{0.3cm} h(X) = 2 \cdot 0.25 \cdot 2 \cdot (2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25) \hspace{0.05cm}.$$
Insbesondere erhält man
- für $\varepsilon = 0.1$:
- $$h(X) =1.9 - 0.525 \cdot {\rm log}_2 \hspace{0.1cm}(5.25) = 1.9 - 1.256 \hspace{0.15cm}\underline{= 0.644\,{\rm bit}} \hspace{0.05cm},$$
- für $\varepsilon = 0.01$:
- $$h(X) =1.99 - 0.5025 \cdot {\rm log}_2 \hspace{0.1cm}(50.25)= 1.99 - 2.84 \hspace{0.15cm}\underline{= -0.850\,{\rm bit}} \hspace{0.05cm}$$
- für $\varepsilon = 0.001$:
- $$h(X) =1.999 - 0.50025 \cdot {\rm log}_2 \hspace{0.1cm}(500.25) = 1.999 - 8.967 \hspace{0.15cm}\underline{= -6.968\,{\rm bit}} \hspace{0.05cm}.$$
(3) Alle Lösungsvorschläge sind zutreffend:
- Nach dem Grenzübergang $\varepsilon → 0$ erhält man für die differentielle Entropie
- $$h(X) = \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0} \hspace{0.1cm}\big[(2-\varepsilon) - (0.5 + 0.25 \cdot \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon +0.25)\big] = 2\,{\rm bit} - 0.5 \cdot \lim\limits_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm} 0}\hspace{0.1cm}{\rm log}_2 \hspace{0.1cm}(0.5/\varepsilon) \hspace{0.3cm}\Rightarrow\hspace{0.3cm} - \infty \hspace{0.05cm}.$$
- Die Wahrscheinlichkeitsdichtefunktion (WDF) ergibt sich in diesem Fall zu
- $$f_X(x) = \left\{ \begin{array}{c} 0.25 + 0.5 \cdot \delta (x-1) \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 2, \\ {\rm sonst} \\ \end{array} \hspace{0.05cm}.$$
Es handelt sich demzufolge um eine „gemischte” Zufallsgröße mit
- einem stochastischen, gleichverteilten Anteil im Bereich $0 \le x \le 2$, und
- einem diskreten Anteil bei $x = 1$ mit der Wahrscheinlichkeit $0.5$.
Die Grafik zeigt links die WDF $f_X(x)$ und rechts die Verteilungsfunktion $F_X(x)$.
(4) Richtig sind die Lösungsvorschläge 2, 3 und 5.
Die untere Grafik zeigt die WDF und die VTF der Zufallsgröße $Y$. Man erkennt:
- $Y$ beinhaltet wie $X$ einen kontinuierlichen und einen diskreten Anteil.
- Der diskrete Anteil tritt mit der Wahrscheinlichkeit ${\rm Pr}(Y = 1) = 0.1$ auf.
- Da $F_Y(y)= {\rm Pr}(Y \le y)$ gilt, ergibt sich der rechtsseitige Grenzwert:
- $$F_Y(y = 1) = 0.55.$$
- Der kontinuierliche Anteil ist nicht gleichverteilt; vielmehr liegt eine Dreieckverteilung vor.
- Richtig ist auch der letzte Vorschlag: $h(Y) = h(X) = - \infty$.
Denn: Bei jeder Zufallsgröße mit einem diskreten Anteil – und ist er auch noch so klein, ist die differentielle Entropie gleich minus unendlich.