Aufgaben:Aufgabe 4.3Z: Hilbert-Transformator: Unterschied zwischen den Versionen
Aus LNTwww
| (7 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID717__Sig_Z_4_3_neu.png|right|frame|Hilbert-Transformator ]] | [[Datei:P_ID717__Sig_Z_4_3_neu.png|right|frame|Hilbert-Transformator ]] | ||
| − | Die Grafik beschreibt ein Modell, wie | + | Die Grafik beschreibt ein Modell, wie zumindest gedanklich, |
| − | Der untere Zweig enthält den so genannten Hilbert–Transformator mit dem Frequenzgang $H_{\rm HT}(f)$. Dessen Ausgangssignal $y(t)$ wird mit der imaginären Einheit $\rm j$ multipliziert und zum Signal $x(t)$ addiert: | + | *aus dem reellen Bandpass–Signal $x(t)$ |
| + | *das analytische Signal $x_{+}(t)$ generiert werden kann. | ||
| + | |||
| + | |||
| + | Der untere Zweig enthält den so genannten „Hilbert–Transformator” mit dem Frequenzgang $H_{\rm HT}(f)$. | ||
| + | |||
| + | Dessen Ausgangssignal $y(t)$ wird mit der imaginären Einheit $\rm j$ multipliziert und zum Signal $x(t)$ addiert: | ||
:$$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$ | :$$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$ | ||
| − | Als Testsignale werden verwendet, jeweils mit $A = 1 \, \text{V}$ und $f_0 = 10 \, \text{kHz}$: | + | Als Testsignale werden verwendet, jeweils mit $A = 1 \, \text{V}$ und $f_0 = 10 \, \text{kHz}$: |
:$$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$ | :$$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$ | ||
:$$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$ | :$$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$ | ||
| − | :$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 (t - \tau) ) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm | + | :$$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm µ s}.$$ |
| + | |||
| + | |||
| + | |||
| Zeile 17: | Zeile 26: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]]. | + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Analytisches_Signal_und_zugehörige_Spektralfunktion|Analytisches Signal und zugehörige Spektralfunktion]]. |
| − | + | ||
*Für die Spektralfunktion des analytischen Signals gilt: | *Für die Spektralfunktion des analytischen Signals gilt: | ||
| − | :$$ X_{\rm +}(f)= \ | + | :$$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$ |
| Zeile 26: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie den Frequenzgang $H_{HT}(f)$ des Hilbert-Transformators. Welcher Wert gilt für die Frequenz $f_0 = 10 \text{kHz}$? | + | {Berechnen Sie den Frequenzgang $H_{\rm HT}(f)$ des Hilbert-Transformators. Welcher Wert gilt für die Frequenz $f_0 = 10 \text{ kHz}$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[H_{\rm HT}(f = f_0)]\ = \ $ { 0. } | $\text{Re}[H_{\rm HT}(f = f_0)]\ = \ $ { 0. } | ||
| − | $\text{ | + | $\text{Im}[H_{\rm HT}(f = f_0)]\ = \ $ { -1.03--0.97 } |
| − | {Wie lautet die Hilbert-Transformierte $y_1(t)$ für das Eingangssignal $x_1(t)$? Welcher Wert ergibt sich insbesondere bei $t = 0$? | + | {Wie lautet die Hilbert-Transformierte $y_1(t)$ für das Eingangssignal $x_1(t)$? Welcher Wert ergibt sich insbesondere bei $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_1(t = 0)\ = \ $ { 0. } $\rm V$ | $y_1(t = 0)\ = \ $ { 0. } $\rm V$ | ||
| − | {Wie lautet die Hilbert-Transformierte $y_2(t)$ für das Eingangssignal $x_2(t)$? Welcher Wert ergibt sich insbesondere bei $t = 0$? | + | {Wie lautet die Hilbert-Transformierte $y_2(t)$ für das Eingangssignal $x_2(t)$? Welcher Wert ergibt sich insbesondere bei $t = 0$? |
|type="{}"} | |type="{}"} | ||
$y_2(t = 0)\ = \ $ { -1.03--0.97 } $\rm V$ | $y_2(t = 0)\ = \ $ { -1.03--0.97 } $\rm V$ | ||
| − | {Wie lautet die Hilbert-Transformierte $y_3(t)$ für das Eingangssignal $x_3(t)$? Wie groß ist die Phasenverzögerung $\varphi_{\rm HT}$ des Hilbert-Transformators? | + | {Wie lautet die Hilbert-Transformierte $y_3(t)$ für das Eingangssignal $x_3(t)$? Welcher Wert ergibt sich für $t=0$? Wie groß ist die Phasenverzögerung $\varphi_{\rm HT}$ des Hilbert-Transformators? |
|type="{}"} | |type="{}"} | ||
$\varphi_{\rm HT}\ = \ $ { 90 3% } $\text{Grad}$ | $\varphi_{\rm HT}\ = \ $ { 90 3% } $\text{Grad}$ | ||
| Zeile 48: | Zeile 57: | ||
| − | {Wie lautet das zu $x_3(t)$ gehörige analytische Signal? | + | {Wie lautet das zu $x_3(t)$ gehörige analytische Signal? Welche Werte haben Real– und Imaginärteil dieses komplexen Signals zum Zeitpunkt $t = 0$? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[x_{3+}(t = 0)]\ = \ $ { 0.707 3% } $\text{V}$ | $\text{Re}[x_{3+}(t = 0)]\ = \ $ { 0.707 3% } $\text{V}$ | ||
| Zeile 59: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Für die Spektralfunktion am Modellausgang gilt: |
:$$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot | :$$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot | ||
X(f).$$ | X(f).$$ | ||
| − | Ein Vergleich mit der angegebenen Beziehung | + | *Ein Vergleich mit der angegebenen Beziehung |
:$$X_{\rm +}(f)= \left(1 + {\rm | :$$X_{\rm +}(f)= \left(1 + {\rm | ||
sign}(f)\right) \cdot X(f)$$ | sign}(f)\right) \cdot X(f)$$ | ||
| − | zeigt, dass $H_{\rm HT}(f) = | + | :zeigt, dass $H_{\rm HT}(f) = - {\rm j} \cdot \sign(f)$ ist. |
| − | '''2 | + | *Der gesuchte Realteil ist somit ${\rm Re}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=0}$ und der Imaginärteil ist gleich ${\rm Im}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=-1}$. |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Aus der Spektralfunktion | ||
:$$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ | :$$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ | ||
{A}/{2}\cdot\delta (f - f_{0}).$$ | {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | wird nach dem Hilbert-Transformator: | + | :wird nach dem Hilbert-Transformator: |
:$$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | :$$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | ||
j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$ | j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | Damit lautet das Signal am Ausgang des Hilbert-Transformators: | + | *Damit lautet das Signal am Ausgang des Hilbert-Transformators: |
:$$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$ | :$$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$ | ||
| − | '''3 | + | |
| + | |||
| + | '''(3)''' Nun lauten die Spektralfunktionen am Eingang und Ausgang des Hilbert-Transformators: | ||
:$$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | :$$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm | ||
j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$ | j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$ | ||
:$$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- | :$$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- | ||
{A}/{2}\cdot\delta (f - f_{0}).$$ | {A}/{2}\cdot\delta (f - f_{0}).$$ | ||
| − | Daraus folgt $y_2(t) = | + | *Daraus folgt $y_2(t) = - A \cdot \cos(2\pi f_0 t)$ und $y_2(t = 0)\; \underline{= -\hspace{-0.08cm}1 \,\text{V}}$. |
| − | '''4 | + | |
| + | |||
| + | |||
| + | '''(4)''' Dieses Eingangssignal lässt sich auch wie folgt darstellen: | ||
:$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - | :$$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - | ||
2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = | 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = | ||
| − | A \cdot {\cos} ( 2 \pi f_0 t - \pi/4). | + | A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} |
| − | + | \Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$ | |
| − | Die Signalphase ist somit $\varphi = \pi /4$. Durch den Hilbert-Transformator wird diese um $\varphi_{\rm HT} \; \underline{= | + | *Die Signalphase ist somit $\varphi = \pi /4$. |
| + | *Durch den Hilbert-Transformator wird diese um $\varphi_{\rm HT} \; \underline{= 90^\circ} \; (\pi /2)$ verzögert. | ||
| + | *Deshalb ist das Ausgangssignal $y_3(t) = A \cdot \cos(2\pi f_0 t -3 \pi /4)$ und der Signalwert zur Zeit $t = 0$ beträgt $A \cdot \cos(135^\circ) \; \underline{= -0.707 \,\text{V}}$. | ||
| − | '''5 | + | |
| + | |||
| + | '''(5)''' Die Spektralfunktion des Signals $x_3(t)$ lautet: | ||
:$$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta | :$$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta | ||
(f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} | (f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} | ||
\varphi}\cdot\delta (f - f_{\rm 0}) .$$ | \varphi}\cdot\delta (f - f_{\rm 0}) .$$ | ||
| − | Beim analytischen Signal verschwindet der erste Anteil und der Anteil bei $+f_0$ wird verdoppelt: | + | *Beim analytischen Signal verschwindet der erste Anteil und der Anteil bei $+f_0$ wird verdoppelt: |
:$$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f | :$$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f | ||
- f_{\rm 0}) .$$ | - f_{\rm 0}) .$$ | ||
| − | Durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]] lautet damit die zugehörige Zeitfunktion mit $\varphi = \pi /4$: | + | *Durch Anwendung des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Verschiebungssatz|Verschiebungssatzes]] lautet damit die zugehörige Zeitfunktion mit $\varphi = \pi /4$: |
:$$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | :$$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | ||
\hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | ||
| − | Speziell gilt für den Zeitpunkt $t = 0$: | + | *Speziell gilt für den Zeitpunkt $t = 0$: |
:$$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} | :$$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} | ||
\varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 | \varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 | ||
| Zeile 106: | Zeile 128: | ||
j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$ | j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$ | ||
| − | ''Hinweis'': Um von $x(t)$ zu $x_+(t)$ zu kommen, muss man nur die Cosinusfunktion durch die komplexe Exponentialfunktion ersetzen. | + | |
| − | Beispielsweise gilt für eine harmonische Schwingung: | + | |
| + | |||
| + | ''Hinweis'': | ||
| + | *Um von $x(t)$ zu $x_+(t)$ zu kommen, muss man nur die Cosinusfunktion durch die komplexe Exponentialfunktion ersetzen. | ||
| + | *Beispielsweise gilt für eine harmonische Schwingung: | ||
:$$x(t) = A \cdot {\cos} ( 2 \pi f_0 t | :$$x(t) = A \cdot {\cos} ( 2 \pi f_0 t | ||
-\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | -\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t | ||
Aktuelle Version vom 6. Mai 2021, 15:49 Uhr
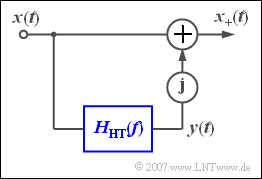
Die Grafik beschreibt ein Modell, wie zumindest gedanklich,
- aus dem reellen Bandpass–Signal $x(t)$
- das analytische Signal $x_{+}(t)$ generiert werden kann.
Der untere Zweig enthält den so genannten „Hilbert–Transformator” mit dem Frequenzgang $H_{\rm HT}(f)$.
Dessen Ausgangssignal $y(t)$ wird mit der imaginären Einheit $\rm j$ multipliziert und zum Signal $x(t)$ addiert:
- $$x_{\rm +}(t)= x(t) + {\rm j}\cdot y(t) .$$
Als Testsignale werden verwendet, jeweils mit $A = 1 \, \text{V}$ und $f_0 = 10 \, \text{kHz}$:
- $$x_1(t) = A \cdot {\cos} ( 2 \pi f_0 t ),$$
- $$x_2(t) = A \cdot {\sin} ( 2 \pi f_0 t ),$$
- $$x_3(t) = A \cdot {\cos} \big( 2 \pi f_0 (t - \tau) \big) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}\tau = 12.5 \hspace{0.1cm}{\rm µ s}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Analytisches Signal und zugehörige Spektralfunktion.
- Für die Spektralfunktion des analytischen Signals gilt:
- $$ X_{\rm +}(f)= \big[1 + {\rm sign}(f)\big] \cdot X(f).$$
Fragebogen
Musterlösung
(1) Für die Spektralfunktion am Modellausgang gilt:
- $$X_{\rm +}(f)= \left(1 + {\rm j}\cdot H_{\rm HT}(f)\right) \cdot X(f).$$
- Ein Vergleich mit der angegebenen Beziehung
- $$X_{\rm +}(f)= \left(1 + {\rm sign}(f)\right) \cdot X(f)$$
- zeigt, dass $H_{\rm HT}(f) = - {\rm j} \cdot \sign(f)$ ist.
- Der gesuchte Realteil ist somit ${\rm Re}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=0}$ und der Imaginärteil ist gleich ${\rm Im}[X_{\rm +}(f)]\hspace{0.15cm}\underline{=-1}$.
(2) Aus der Spektralfunktion
- $$X_1(f) = {A}/{2}\cdot\delta (f + f_{0})+ {A}/{2}\cdot\delta (f - f_{0}).$$
- wird nach dem Hilbert-Transformator:
- $$Y_1(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}).$$
- Damit lautet das Signal am Ausgang des Hilbert-Transformators:
- $$y_1(t) = A \cdot {\sin} ( 2 \pi f_0 t ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}y_1(t=0)\hspace{0.15 cm}\underline{ =0}.$$
(3) Nun lauten die Spektralfunktionen am Eingang und Ausgang des Hilbert-Transformators:
- $$X_2(f) = {\rm j}\cdot {A}/{2}\cdot\delta (f + f_{0})-{\rm j}\cdot {A}/{2}\cdot\delta (f - f_{0}),$$
- $$Y_2(f) = -{A}/{2}\cdot\delta (f + f_{0})- {A}/{2}\cdot\delta (f - f_{0}).$$
- Daraus folgt $y_2(t) = - A \cdot \cos(2\pi f_0 t)$ und $y_2(t = 0)\; \underline{= -\hspace{-0.08cm}1 \,\text{V}}$.
(4) Dieses Eingangssignal lässt sich auch wie folgt darstellen:
- $$x_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot {\rm 0.0125 \hspace{0.05cm} ms}) = A \cdot {\cos} ( 2 \pi f_0 t - \pi/4)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}y_3(t) = A \cdot {\cos} ( 2 \pi f_0 t - 3\pi/4).$$
- Die Signalphase ist somit $\varphi = \pi /4$.
- Durch den Hilbert-Transformator wird diese um $\varphi_{\rm HT} \; \underline{= 90^\circ} \; (\pi /2)$ verzögert.
- Deshalb ist das Ausgangssignal $y_3(t) = A \cdot \cos(2\pi f_0 t -3 \pi /4)$ und der Signalwert zur Zeit $t = 0$ beträgt $A \cdot \cos(135^\circ) \; \underline{= -0.707 \,\text{V}}$.
(5) Die Spektralfunktion des Signals $x_3(t)$ lautet:
- $$X_3(f) = {A_0}/{2} \cdot {\rm e}^{{\rm j} \varphi}\cdot\delta (f + f_{\rm 0}) + {A_0}/{2} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$
- Beim analytischen Signal verschwindet der erste Anteil und der Anteil bei $+f_0$ wird verdoppelt:
- $$X_{3+}(f) = {A_0} \cdot {\rm e}^{-{\rm j} \varphi}\cdot\delta (f - f_{\rm 0}) .$$
- Durch Anwendung des Verschiebungssatzes lautet damit die zugehörige Zeitfunktion mit $\varphi = \pi /4$:
- $$x_{3+}(t) = A_0 \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
- Speziell gilt für den Zeitpunkt $t = 0$:
- $$x_{3+}(t = 0) = A_0 \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \varphi} = A_0 \cdot{\cos} ( 45^\circ)-{\rm j}\cdot A_0 \cdot{\sin} ( 45^\circ)= \hspace{0.15 cm}\underline{{\rm 0.707 \hspace{0.05cm} V}-{\rm j}\cdot {\rm 0.707 \hspace{0.05cm} V}}.$$
Hinweis:
- Um von $x(t)$ zu $x_+(t)$ zu kommen, muss man nur die Cosinusfunktion durch die komplexe Exponentialfunktion ersetzen.
- Beispielsweise gilt für eine harmonische Schwingung:
- $$x(t) = A \cdot {\cos} ( 2 \pi f_0 t -\hspace{0.05cm} \varphi) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{+}(t) = A \cdot {\rm e}^{{\rm j}( 2 \pi f_{\rm 0} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$