Lineare zeitinvariante Systeme/Laplace–Rücktransformation: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Aufgabenstellung:}$ Dieses Kapitel behandelt das folgende Problem: | $\text{Aufgabenstellung:}$ Dieses Kapitel behandelt das folgende Problem: | ||
| − | *Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. | + | *Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form. |
| − | *Gesucht ist die '''Laplace–Rücktransformierte''', also die dazugehörige Zeitfunktion $y(t)$, wobei folgende Notation gelten soll: | + | *Gesucht ist die '''Laplace–Rücktransformierte''', also die dazugehörige Zeitfunktion $y(t)$, wobei folgende Notation gelten soll: |
:$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} | :$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} | ||
y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$}} | y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$}} | ||
| Zeile 17: | Zeile 17: | ||
In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt. | In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt. | ||
| − | [[Datei:P_ID1770__LZI_T_3_3_S1_neu.png | | + | [[Datei:P_ID1770__LZI_T_3_3_S1_neu.png |right|frame| Voraussetzungen für das Kapitel „Laplace–Rücktransformation”]] |
| − | *$H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem und $Y_{\rm L}(p)$ gibt die Laplace–Transformierte des Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ an. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$ | + | *$H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem und $Y_{\rm L}(p)$ gibt die Laplace–Transformierte des Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ an. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$ |
| − | *Die Pole und Nullstellen zeigen die im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Eigenschaften_der_Pole_und_Nullstellen|letzten Kapitel]] genannten Eigenschaften: Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind dagegen auch in der rechten $p$–Halbebene erlaubt. | + | *Die Pole und Nullstellen zeigen die im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Eigenschaften_der_Pole_und_Nullstellen|letzten Kapitel]] genannten Eigenschaften: Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind dagegen auch in der rechten $p$–Halbebene erlaubt. |
| − | *Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind | + | *Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind erlaubt. |
| − | *Verwendet man das Eingangssignal $x(t) = δ(t) | + | *Verwendet man das Eingangssignal $x(t) = δ(t)$ ⇒ $ X_{\rm L}(p) = 1 $ ⇒ $ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt $y(t)$ die [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Impulsantwort|Impulsantwort]] $h(t)$ des Übertragungssystems. Zur Berechnung dürfen hierfür nur die in der Grafik grün eingezeichneten Singularitäten herangezogen werden. |
| − | *Eine Sprungfunktion $x(t) = γ(t) ⇒ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Sprungantwort|Sprungantwort]] | + | *Eine Sprungfunktion $x(t) = γ(t) \ \ ⇒ \ \ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich#Sprungantwort|Sprungantwort]] $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p = 0$ zu berücksichtigen. |
| − | *Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Einige_wichtige_Laplace.E2.80.93Korrespondenzen|Tabelle]] im Kapitel „Laplace–Transformation und $p$–Übertragungsfunktion”), zum Beispiel ein zum Zeitpunkt $t = 0$ eingeschaltetes Cosinus– oder Sinussignal. | + | *Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Einige_wichtige_Laplace.E2.80.93Korrespondenzen|Tabelle]] im Kapitel „Laplace–Transformation und $p$–Übertragungsfunktion”), zum Beispiel ein zum Zeitpunkt $t = 0$ eingeschaltetes Cosinus– oder Sinussignal. |
| − | *Bei der hier beschriebenen Vorgehensweise ist also ein Rechteck als Eingangssignal $x(t) ⇒ X_{\rm L}(p) = (1 | + | *Bei der hier beschriebenen Vorgehensweise ist also ein Rechteck als Eingangssignal $x(t)\ \ ⇒ \ \ X_{\rm L}(p) = (1 - {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm} T})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden. |
==Einige Ergebnisse der Funktionentheorie== | ==Einige Ergebnisse der Funktionentheorie== | ||
<br> | <br> | ||
| − | Im Gegensatz zu den [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Fourierintegralen]], die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei „Laplace” die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation – | + | Im Gegensatz zu den [[Signaldarstellung/Fouriertransformation_und_-rücktransformation#Das_erste_Fourierintegral|Fourierintegralen]], die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei „Laplace” die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation – |
| − | *sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$, | + | *sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$, |
*auf elementarem Weg nicht oder nur sehr umständlich lösbar. | *auf elementarem Weg nicht oder nur sehr umständlich lösbar. | ||
| Zeile 36: | Zeile 36: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | Allgemein gilt für die '''Laplace–Rücktransformation''': | + | Allgemein gilt für die '''Laplace–Rücktransformation''': |
| − | :$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{ {\rm j} \cdot 2 \pi}\cdot | + | :$$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{ {\rm j} \cdot 2 \pi}\cdot \int_{ \alpha - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta } ^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm}{\rm |
d}p \hspace{0.05cm} .$$ | d}p \hspace{0.05cm} .$$ | ||
| − | Die Integration erfolgt parallel zur imaginären Achse. Der Realteil $α$ ist | + | *Die Integration erfolgt parallel zur imaginären Achse. |
| + | *Der Realteil $α$ ist so zu wählen, dass alle Pole links vom Integrationsweg liegen.}} | ||
| − | [[Datei:P_ID1777__LZI_T_3_3_S2_neu.png | | + | [[Datei:P_ID1777__LZI_T_3_3_S2_neu.png |right|frame| Linienintegral sowie linkes und rechtes Kreisintegral]] |
| − | Die linke Grafik verdeutlicht dieses Linienintegral entlang der rot gepunkteten Vertikalen ${\rm Re}\{p\}= α$. Lösbar ist dieses Integral mit dem [https://de.wikipedia.org/wiki/Lemma_von_Jordan Jordanschen Lemma der Funktionstheorie]. | + | Die linke Grafik verdeutlicht dieses Linienintegral entlang der rot gepunkteten Vertikalen ${\rm Re}\{p\}= α$. Lösbar ist dieses Integral mit dem [https://de.wikipedia.org/wiki/Lemma_von_Jordan Jordanschen Lemma der Funktionstheorie]. Hier folgt nur eine sehr kurze und einfache Zusammenfassung der Vorgehensweise: |
| − | *Das Linienintegral kann | + | *Das Linienintegral kann in zwei Kreisintegrale aufgeteilt werden, wobei sämtliche Polstellen im linken Kreisintegral liegen, während das rechte Kreisintegral nur Nullstellen beinhalten darf. |
| − | *Entsprechend der Funktionstheorie liefert das rechte Kreisintegral die Zeitfunktion $y(t)$ für negative Zeiten. Aufgrund der Kausalität | + | *Entsprechend der Funktionstheorie liefert das rechte Kreisintegral die Zeitfunktion $y(t)$ für negative Zeiten. Aufgrund der Kausalität ist $y(t < 0) \equiv 0$, sein. Dies trifft aber nur dann zu, wenn es in der rechten $p$–Halbebene keine Pole gibt. |
| − | *Das Integral über den linken Halbkreis liefert | + | *Das Integral über den linken Halbkreis liefert die Zeitfunktion für $t ≥ 0$. Dieses umschließt alle Pole und ist mit dem Residuensatz in (relativ) einfacher Weise berechenbar, wie auf den nächsten Seiten gezeigt wird. |
==Formulierung des Residuensatzes== | ==Formulierung des Residuensatzes== | ||
<br> | <br> | ||
| − | Es wird weiter vorausgesetzt, dass die Übertragungsfunktion $Y_{\rm L}(p)$ in Pol–Nullstellen–Form durch | + | Es wird weiter vorausgesetzt, dass die Übertragungsfunktion $Y_{\rm L}(p)$ in Pol–Nullstellen–Form durch |
| − | *den konstanten Faktor $K$, | + | *den konstanten Faktor $K$, |
| − | *die $Z$ Nullstellen $p_{{\rm o}i} (i =$ | + | *die $Z$ Nullstellen $p_{{\rm o}i}$ $(i = 1$, ... , $Z)$ und |
| − | *die $N$ Polstellen $p_{{\rm x}i} (i =$ | + | *die $N$ Polstellen $p_{{\rm x}i}$ $(i = 1$, ... , $N$) |
| − | dargestellt werden kann. Wir setzen zudem $Z < N$ | + | dargestellt werden kann. Wir setzen zudem $Z < N$ voraus. |
| − | |||
| − | |||
| − | |||
| + | Die Anzahl der unterscheidbaren Pole bezeichnen wir mit $I$. Zur Bestimung von $I$ werden mehrfache Pole nur einfach gezählt. So gilt für die [[Lineare_zeitinvariante_Systeme/Laplace–Rücktransformation#Einige_Ergebnisse_der_Funktionentheorie|Skizze]] im letzten Abschnitt (unter Berücksichtigung des Poles bei $p=0$) aufgrund der doppelten Polstelle: $N = 5$ und $I = 4$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Residuensatz:}$ | $\text{Residuensatz:}$ | ||
| − | Unter den genannten Voraussetzungen ergibt sich die '''Laplace–Rücktransformierte''' von $Y_{\rm L}(p)$ für Zeiten $t ≥$ | + | Unter den genannten Voraussetzungen ergibt sich die '''Laplace–Rücktransformierte''' von $Y_{\rm L}(p)$ für Zeiten $t ≥ 0$ als die Summe von $I$ Eigenschwingungen der Pole, die man als die '''Residuen''' – abgekürzt mit „Res” – bezeichnet: |
:$$y(t) = \sum_{i=1}^{I}{\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}_i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p \hspace{0.05cm}t}\} \hspace{0.05cm} .$$ | :$$y(t) = \sum_{i=1}^{I}{\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}_i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p \hspace{0.05cm}t}\} \hspace{0.05cm} .$$ | ||
| − | Da $Y_{\rm L}(p)$ nur für kausale Signale angebbar ist, gilt für negative Zeiten stets $y(t < 0) = 0$. | + | Da $Y_{\rm L}(p)$ nur für kausale Signale angebbar ist, gilt für negative Zeiten stets $y(t < 0) = 0$. |
| − | + | *Für einen Pol der Vielfachheit $l$ gilt allgemein: | |
| − | Für einen | ||
:$${\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{1}{(l-1)!}\cdot \frac{ {\rm d}^{\hspace{0.05cm}l-1} }{ {\rm d}p^{\hspace{0.05cm}l-1} }\hspace{0.15cm} \left \{Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i})^{\hspace{0.05cm}l}\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg \vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$ | :$${\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{1}{(l-1)!}\cdot \frac{ {\rm d}^{\hspace{0.05cm}l-1} }{ {\rm d}p^{\hspace{0.05cm}l-1} }\hspace{0.15cm} \left \{Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i})^{\hspace{0.05cm}l}\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg \vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$ | ||
| − | Als Sonderfall ergibt sich daraus mit $l = 1$ für einen | + | *Als Sonderfall ergibt sich daraus mit $l = 1$ für einen einfachen Pol: |
:$${\rm Res} \bigg\vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i} )\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$}} | :$${\rm Res} \bigg\vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i} )\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$}} | ||
| − | + | Auf den nächsten Seiten wird der Residuensatz anhand dreier ausführlicher Beispiele verdeutlicht, die mit den drei Konstellationen im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Eigenschaften_der_Pole_und_Nullstellen| $\text{Beispiel 3}$]] im Kapitel „Laplace–Transformation” korrespondieren: | |
| − | Auf den nächsten Seiten wird der Residuensatz anhand dreier ausführlicher Beispiele verdeutlicht, die mit den drei Konstellationen im [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Eigenschaften_der_Pole_und_Nullstellen| Beispiel 3]] im Kapitel „Laplace–Transformation” korrespondieren: | + | *Wir betrachten also wieder den Vierpol mit einer Induktivität $L = 25 \ \rm µH$ im Längszweig sowie im Querzweig die Serienschaltung aus einem Ohmschen Widerstand $R = 50 \ \rm Ω$ und einer Kapazität $C$. |
| − | *Wir betrachten also wieder den Vierpol mit einer Induktivität $L = 25 \ \rm µH$ im Längszweig sowie im Querzweig die Serienschaltung aus einem Ohmschen Widerstand $R = 50 \ \rm Ω$ und einer Kapazität $C$. | + | *Für Letztere betrachten wir wieder drei verschiedene Werte, nämlich $C = 62.5 \ \rm nF$, $C = 8 \ \rm nF$ und $C = 40 \ \rm nF$. |
| − | *Für Letztere betrachten wir wieder drei verschiedene Werte, nämlich $C = 62.5 \ \rm nF$, $C = 8 \ \rm nF$ und $C = 40 \ \rm nF$. | + | *Vorausgesetzt ist stets $x(t) = δ(t) \; ⇒ \; X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$ ⇒ $y(t)$ ist gleich der Impulsantwort $h(t)$. |
| − | *Vorausgesetzt ist stets $x(t) = δ(t) \; ⇒ \; X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$ ⇒ | ||
==Aperiodisch abklingende Impulsantwort== | ==Aperiodisch abklingende Impulsantwort== | ||
<br> | <br> | ||
| − | Mit der Kapazität $C = 62.5 \ \rm nF$ und den weiteren in der unteren Grafik angegebenen Zahlenwerten erhält man für die auf der Seite [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Pol.E2.80.93Nullstellen.E2.80.93Darstellung_von_Schaltungen|Pol–Nullstellen–Darstellung von Schaltungen]] berechnete $p$–Übertragungsfunktion: | + | Mit der Kapazität $C = 62.5 \ \rm nF$ und den weiteren in der unteren Grafik angegebenen Zahlenwerten erhält man für die auf der Seite [[Lineare_zeitinvariante_Systeme/Laplace–Transformation_und_p–Übertragungsfunktion#Pol.E2.80.93Nullstellen.E2.80.93Darstellung_von_Schaltungen|Pol–Nullstellen–Darstellung von Schaltungen]] berechnete $p$–Übertragungsfunktion: |
| + | [[Datei: P_ID1772__LZI_T_3_3_S3a_kurz.png |right|frame| Abklingende Impulsantwort]] | ||
| + | |||
:$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})}= 2 \cdot \frac {p + 0.32 } | :$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})}= 2 \cdot \frac {p + 0.32 } | ||
{(p +0.4)(p +1.6 )} \hspace{0.05cm} .$$ | {(p +0.4)(p +1.6 )} \hspace{0.05cm} .$$ | ||
| − | Beachten Sie bitte die Normierung von $p$, $K$ sowie aller Pole und Nullstellen mit dem Faktor ${\rm 10^6} · 1/\rm s$. | + | Beachten Sie bitte die Normierung von $p$, $K$ sowie aller Pole und Nullstellen mit dem Faktor ${\rm 10^6} · 1/\rm s$. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die Impulsantwort setzt sich aus $I = N = 2$ Eigenschwingungen zusammen. Für $t < 0$ sind diese gleich Null. | |
| + | *Das Residium des Pols bei $p_{{\rm x}1} =\ –0.4$ liefert folgende Zeitfunktion: | ||
| + | :$$h_1(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}1})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}$$ | ||
| + | : $$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {p + 0.32 } {p +0.4}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.4}= - \frac {2 } {15}\cdot {\rm e}^{-0.4 \hspace{0.05cm} t} \hspace{0.05cm}. $$ | ||
| + | *Für das Residium des zweiten Pols bei $p_{{\rm x}2} = \ –1.6$ gilt: | ||
| + | :$$h_2(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}2})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}h_2(t) = 2 \cdot \frac {p + 0.32 } {p +1.6}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1.6}= \frac {32 } {15}\cdot {\rm e}^{-1.6 \hspace{0.05cm} t} \hspace{0.05cm}. $$ | ||
| − | Die Grafik zeigt $h_1(t)$ und $h_2(t)$ sowie das Summensignal $h(t)$. Berücksichtigt ist auch hier der Normierungsfaktor $1/T = 10^6 · \rm 1/s$, so dass die Zeit auf $T = 1 \ \rm µ s$ normiert ist. Für $t =0$ ergibt sich | + | Die Grafik zeigt $h_1(t)$ und $h_2(t)$ sowie das Summensignal $h(t)$. |
| − | + | *Berücksichtigt ist auch hier der Normierungsfaktor $1/T = 10^6 · \rm 1/s$, so dass die Zeit auf $T = 1 \ \rm µ s$ normiert ist. | |
| − | Für Zeiten $t > 2 \ \rm µ s$ ist die Impulsantwort negativ (wenn auch nur geringfügig und in der Grafik nur schwer zu erkennen). | + | *Für $t =0$ ergibt sich $T \cdot h(t=0) = {32 }/ {15} -{2 }/ {15}= 2 \hspace{0.05cm}$. |
| + | *Für Zeiten $t > 2 \ \rm µ s$ ist die Impulsantwort negativ (wenn auch nur geringfügig und in der Grafik nur schwer zu erkennen). | ||
<br clear=all> | <br clear=all> | ||
==Gedämpft oszillierende Impulsantwort== | ==Gedämpft oszillierende Impulsantwort== | ||
<br> | <br> | ||
| − | Die Bauelementewerte $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 8 \ \rm nF$ ergeben zwei konjugiert komplexe Pole bei $p_{{\rm x}1} = \ –1 + {\rm j} · 2$ und $p_{{\rm x}2} = \ –1 - {\rm j} · 2$. Die Nullstelle liegt bei $p_{\rm o} = \ –2.5$. Es gilt $K = 2$ und alle Zahlenwerte sind wieder mit dem Faktor $1/T$ zu multiplizieren $(T = 1\ \rm µ s$). | + | Die Bauelementewerte $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 8 \ \rm nF$ ergeben zwei konjugiert komplexe Pole bei $p_{{\rm x}1} = \ –1 + {\rm j} · 2$ und $p_{{\rm x}2} = \ –1 - {\rm j} · 2$. |
| + | [[Datei:P_ID1780__LZI_T_3_3_S3b_kurz.png |right|frame| Gedämpft oszillierende Impulsantwort]] | ||
| + | *Die Nullstelle liegt bei $p_{\rm o} = \ –2.5$. | ||
| + | *Es gilt $K = 2$ und alle Zahlenwerte sind wieder mit dem Faktor $1/T$ zu multiplizieren $(T = 1\ \rm µ s$). | ||
| + | |||
Wendet man den Residuensatz auf diese Konfiguration an, so erhält man: | Wendet man den Residuensatz auf diese Konfiguration an, so erhält man: | ||
| − | :$$h_1(t) = | + | :$$h_1(t) = K \cdot \frac {p_{\rm x 1} - p_{\rm o }} {p_{\rm x 1} - p_{\rm x 2}} \cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot \hspace{0.05cm}t} $$ |
| − | \cdot\hspace{0.05cm}t}= 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= (1 - {\rm j}\cdot 0.75)\cdot {\rm | + | :$$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {-1 + {\rm j}\cdot 2 +2.5} {(-1 + {\rm j}\cdot 2) - (-1 - {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} |
| + | \cdot\hspace{0.05cm}t}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= (1 - {\rm j}\cdot 0.75)\cdot {\rm | ||
e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} ,$$ | e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} ,$$ | ||
| − | |||
| − | Mit dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] ergibt sich somit für das Summensignal: | + | :$$ h_2(t) = K \cdot \frac {p_{\rm x 2} - p_{\rm o }} {p_{\rm x 2} - p_{\rm x 1}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot \hspace{0.05cm}t} $$ |
| − | :$$h(t) = h_1(t) + h_2(t) = {\rm e}^{-t}\cdot \ | + | :$$\Rightarrow \hspace{0.3cm} h_2(t) = 2 \cdot \frac {-1 - {\rm j}\cdot 2 +2.5} {(-1 - {\rm j}\cdot 2) - (-1 + {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t} $$ |
| − | (1 + {\rm j}\cdot 0.75)\cdot (\cos() - {\rm j}\cdot \sin())\ | + | :$$\Rightarrow \hspace{0.3cm}h_2(t) =2 \cdot \frac {1.5 - {\rm j}\cdot 2} {-{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t}= (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} $$ |
| + | :$$\Rightarrow \hspace{0.3cm}h_2(t) = (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} . $$ | ||
| + | |||
| + | Mit dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] ergibt sich somit für das Summensignal: | ||
| + | :$$h(t) = h_1(t) + h_2(t)\hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm}h(t) = {\rm e}^{-t}\cdot \big [ (1 - {\rm j}\cdot 0.75)\cdot (\cos() + {\rm j}\cdot \sin())+ | ||
| + | + (1 + {\rm j}\cdot 0.75)\cdot (\cos() - {\rm j}\cdot \sin())\big ]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}h(t) ={\rm e}^{-t}\cdot \big [ 2\cdot \cos(2t) + 1.5 \cdot \sin(2t)\big ]\hspace{0.05cm} . $$ | ||
| − | + | Die Grafik zeigt die nun mit ${\rm e}^{–t}$ gedämpft oszillierende Impulsantwort $h(t)$ für diese Pol–Nullstellen–Konfiguration. | |
| − | Die Grafik | ||
<br clear=all> | <br clear=all> | ||
==Aperiodischer Grenzfall== | ==Aperiodischer Grenzfall== | ||
<br> | <br> | ||
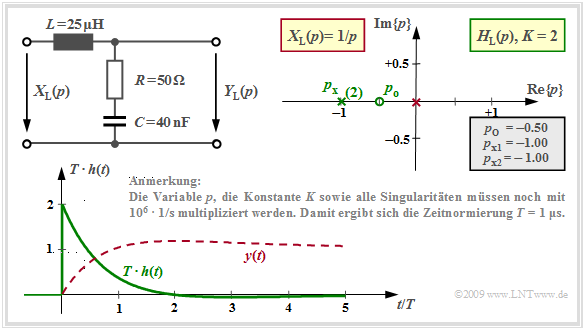
| − | Mit $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 40 \ \rm nF$ ergibt sich der so genannte aperiodische Grenzfall: | + | Mit $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 40 \ \rm nF$ ergibt sich der so genannte aperiodische Grenzfall: |
:$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x })^2}= 2 \cdot \frac {p + 0.5 } {(p +1)^2} \hspace{0.05cm} .$$ | :$$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x })^2}= 2 \cdot \frac {p + 0.5 } {(p +1)^2} \hspace{0.05cm} .$$ | ||
| − | Der Kapazitätswert $C = 40 \ \rm nF$ ist der kleinstmögliche Wert, für den sich gerade noch reelle Polstellen ergeben. Diese fallen zusammen, das heißt $p_{\rm x} = \ –1$ ist eine doppelte Polstelle. Die Zeitfunktion lautet somit entsprechend dem Residuensatz mit $l = 2$: | + | Der Kapazitätswert $C = 40 \ \rm nF$ ist der kleinstmögliche Wert, für den sich gerade noch reelle Polstellen ergeben. Diese fallen zusammen, das heißt $p_{\rm x} = \ –1$ ist eine doppelte Polstelle. Die Zeitfunktion lautet somit entsprechend dem Residuensatz mit $l = 2$: |
:$$h(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm} | :$$h(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm} | ||
\left \{H_{\rm L}(p)\cdot (p - p_{ {\rm x} })^2\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } = K \cdot \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm}\left \{ (p - p_{ {\rm o} })\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{0.05cm} .$$ | \left \{H_{\rm L}(p)\cdot (p - p_{ {\rm x} })^2\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } = K \cdot \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm}\left \{ (p - p_{ {\rm o} })\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{0.05cm} .$$ | ||
| − | Mit der | + | [[Datei:P_ID1774__LZI_T_3_3_S3c_kurz.png |right|frame| Impulsantwort (grün) und Sprungantwort (rot) des aperiodischen Grenzfalls]] |
| + | |||
| + | Mit der Produktregel der Differentialrechnung ergibt sich daraus: | ||
:$$h(t) = K \cdot \left [ {\rm e}^{p \hspace{0.05cm}t} + (p - p_{ {\rm o} })\cdot t \cdot {\rm e}^{p \hspace{0.05cm}t} \right ] \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1} = {\rm e}^{-t}\cdot \left ( 2 - t \right) | :$$h(t) = K \cdot \left [ {\rm e}^{p \hspace{0.05cm}t} + (p - p_{ {\rm o} })\cdot t \cdot {\rm e}^{p \hspace{0.05cm}t} \right ] \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1} = {\rm e}^{-t}\cdot \left ( 2 - t \right) | ||
\hspace{0.05cm} .$$ | \hspace{0.05cm} .$$ | ||
| − | + | *Die Grafik zeigt diese '''Impulsantwort''' als grüne Kurve in normierter Darstellung. Sie unterscheidet sich von derjenigen mit den beiden unterschiedlichen Polen bei $-0.4$ und $-1.6$ nur geringfügig. | |
| + | |||
| + | *Das rot gezeichnete Signal $y(t) = 1 - {\rm e}^{-t} + t \cdot {\rm e}^{-t}$ ergibt sich, wenn am Eingang zusätzlich eine Sprungfunktion berücksichtigt wird. | ||
| + | |||
| − | + | Zur Berechnung der '''Sprungantwort''' $\sigma(t) = y(t)$ kann man alternativ | |
| + | :*bei der Residuenberechnung einen zusätzlichen Pol bei $p = 0$ (rot markiert) berücksichtigen, oder | ||
| + | :*das Integral über die Impulsantwort $h(t)$ bilden. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Partialbruchzerlegung== | ==Partialbruchzerlegung== | ||
<br> | <br> | ||
| − | Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt | + | Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt ⇒ $Z$ muss stets kleiner als $N$ sein. |
| − | Gilt dagegen wie bei einem Hochpass $Z = N$, so | + | Gilt dagegen wie bei einem Hochpass $Z = N$, so |
| − | *ist der Grenzwert der Spektralfunktion für großes $p$ ungleich | + | *ist der Grenzwert der Spektralfunktion für großes $p$ ungleich Null, |
| − | *beinhaltet das zugehörige Zeitsignal $y(t)$ auch einen [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale#Diracimpuls|Diracimpuls]], | + | *beinhaltet das zugehörige Zeitsignal $y(t)$ auch einen [[Signaldarstellung/Einige_Sonderfälle_impulsartiger_Signale#Diracimpuls|Diracimpuls]], |
| − | *versagt der Residuensatz und es ist eine ''Partialbruchzerlegung'' vorzunehmen. | + | *versagt der Residuensatz und es ist eine [https://de.wikipedia.org/wiki/Partialbruchzerlegung '''Partialbruchzerlegung'''] vorzunehmen. |
| Zeile 158: | Zeile 171: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 1:}$ | $\text{Beispiel 1:}$ | ||
| − | Die $p$–Übertragungsfunktion eines | + | Die $p$–Übertragungsfunktion eines RC–Hochpasses erster Ordnung kann durch Abspaltung einer Konstanten wie folgt umgewandelt werden: |
| − | $$\frac{p}{p + RC} = 1- \frac{RC}{p + RC}\hspace{0.05cm} .$$ | + | :$$\frac{p}{p + RC} = 1- \frac{RC}{p + RC}\hspace{0.05cm} .$$ |
| − | Damit lautet die Impulsantwort | + | Damit lautet die Hochpass–Impulsantwort: |
| − | $$h_{\rm HP}(t) = \delta(t) - h_{\rm TP}(t) \hspace{0.05cm} .$$ | + | :$$h_{\rm HP}(t) = \delta(t) - h_{\rm TP}(t) \hspace{0.05cm} .$$ |
| + | |||
Die Grafik zeigt | Die Grafik zeigt | ||
| − | *als rote Kurve die Impulsantwort $h_{\rm HP}(t)$ | + | *als rote Kurve die Hochpass–Impulsantwort $h_{\rm HP}(t)$, |
| − | * als blaue Kurve die Impulsantwort $h_{\rm TP}(t)$ des äquivalenten Tiefpasses. | + | * als blaue Kurve die Impulsantwort $h_{\rm TP}(t)$ des äquivalenten Tiefpasses. |
| − | |||
| − | Die Diracfunktion ist die Laplace–Transformierte des konstanten Wertes | + | Die Diracfunktion ist die Laplace–Transformierte des konstanten Wertes $1$, während die zweite, zu subtrahierende Funktion die Impulsantwort des äquivalenten Tiefpasses angibt, die durch den Residuensatz angebbar ist mit den Parametern |
| + | :$$Z = 0,\hspace{0.2cm} N =1,\hspace{0.2cm} K = RC.$$ }} | ||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
Aktuelle Version vom 18. Oktober 2021, 10:19 Uhr
Inhaltsverzeichnis
Problemstellung und Voraussetzungen
$\text{Aufgabenstellung:}$ Dieses Kapitel behandelt das folgende Problem:
- Bekannt ist die $p$–Spektralfunktion $Y_{\rm L}(p)$ in der Pol–Nullstellen–Form.
- Gesucht ist die Laplace–Rücktransformierte, also die dazugehörige Zeitfunktion $y(t)$, wobei folgende Notation gelten soll:
- $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}\hspace{0.05cm} , \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} y(t) \quad \circ\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\bullet\quad Y_{\rm L}(p)\hspace{0.05cm} .$$
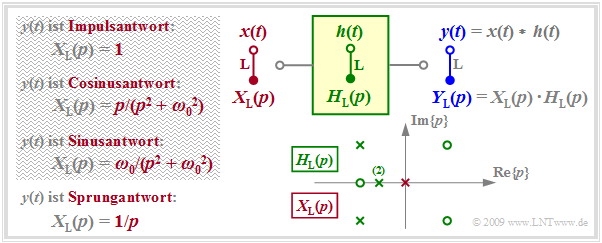
In der Grafik sind die Voraussetzungen für diese Aufgabenstellung zusammengestellt.
- $H_{\rm L}(p)$ beschreibt das kausale Übertragungssystem und $Y_{\rm L}(p)$ gibt die Laplace–Transformierte des Ausgangssignals $y(t)$ unter Berücksichtigung des Eingangssignals $x(t)$ an. $Y_{\rm L}(p)$ ist gekennzeichnet durch $N$ Pole, durch $Z ≤ N$ Nullstellen sowie durch die Konstante $K.$
- Die Pole und Nullstellen zeigen die im letzten Kapitel genannten Eigenschaften: Pole dürfen nur in der linken $p$–Halbebene oder auf der imaginären Achse liegen, Nullstellen sind dagegen auch in der rechten $p$–Halbebene erlaubt.
- Alle Singularitäten – dies ist der Oberbegriff für Pole und Nullstellen – sind entweder reell oder es treten Paare von konjugiert–komplexen Singularitäten auf. Mehrfache Pole und Nullstellen sind erlaubt.
- Verwendet man das Eingangssignal $x(t) = δ(t)$ ⇒ $ X_{\rm L}(p) = 1 $ ⇒ $ Y_{\rm L}(p) = H_{\rm L}(p)$, so beschreibt $y(t)$ die Impulsantwort $h(t)$ des Übertragungssystems. Zur Berechnung dürfen hierfür nur die in der Grafik grün eingezeichneten Singularitäten herangezogen werden.
- Eine Sprungfunktion $x(t) = γ(t) \ \ ⇒ \ \ X_{\rm L} = 1/p$ am Eingang bewirkt, dass das Ausgangssignal $y(t)$ gleich der Sprungantwort $σ(t)$ von $H_{\rm L}(p)$ ist. Zur Berechnung ist neben den Singularitäten von $H_{\rm L}(p)$ nun auch die (in der Grafik rot eingezeichnete) Polstelle bei $p = 0$ zu berücksichtigen.
- Als Eingang $x(t)$ sind nur Signale möglich, für die $X_{ \rm L}(p)$ in Pol–Nullstellen–Form darstellbar ist (siehe Tabelle im Kapitel „Laplace–Transformation und $p$–Übertragungsfunktion”), zum Beispiel ein zum Zeitpunkt $t = 0$ eingeschaltetes Cosinus– oder Sinussignal.
- Bei der hier beschriebenen Vorgehensweise ist also ein Rechteck als Eingangssignal $x(t)\ \ ⇒ \ \ X_{\rm L}(p) = (1 - {\rm e}^{\hspace{0.05cm}p\hspace{0.05cm}\cdot \hspace{0.05cm} T})/p$ nicht möglich. Die Rechteckantwort $y(t)$ kann aber als Differenz zweier Sprungantworten indirekt berechnet werden.
Einige Ergebnisse der Funktionentheorie
Im Gegensatz zu den Fourierintegralen, die sich in den beiden Transformationsrichtungen nur geringfügig unterscheiden, ist bei „Laplace” die Berechnung von $y(t)$ aus $Y_{\rm L}(p)$ – also die Rücktransformation –
- sehr viel schwieriger als die Berechnung von $Y_{\rm L}(p)$ aus $y(t)$,
- auf elementarem Weg nicht oder nur sehr umständlich lösbar.
$\text{Definition:}$ Allgemein gilt für die Laplace–Rücktransformation:
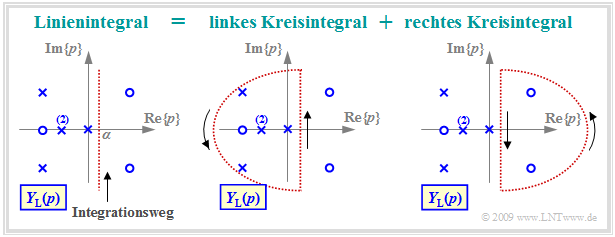
- $$y(t) = {\rm L}^{-1}\{Y_{\rm L}(p)\}= \lim_{\beta \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} \hspace{0.15cm} \frac{1}{ {\rm j} \cdot 2 \pi}\cdot \int_{ \alpha - {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta } ^{\alpha+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \beta} Y_{\rm L}(p) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm}{\rm d}p \hspace{0.05cm} .$$
- Die Integration erfolgt parallel zur imaginären Achse.
- Der Realteil $α$ ist so zu wählen, dass alle Pole links vom Integrationsweg liegen.
Die linke Grafik verdeutlicht dieses Linienintegral entlang der rot gepunkteten Vertikalen ${\rm Re}\{p\}= α$. Lösbar ist dieses Integral mit dem Jordanschen Lemma der Funktionstheorie. Hier folgt nur eine sehr kurze und einfache Zusammenfassung der Vorgehensweise:
- Das Linienintegral kann in zwei Kreisintegrale aufgeteilt werden, wobei sämtliche Polstellen im linken Kreisintegral liegen, während das rechte Kreisintegral nur Nullstellen beinhalten darf.
- Entsprechend der Funktionstheorie liefert das rechte Kreisintegral die Zeitfunktion $y(t)$ für negative Zeiten. Aufgrund der Kausalität ist $y(t < 0) \equiv 0$, sein. Dies trifft aber nur dann zu, wenn es in der rechten $p$–Halbebene keine Pole gibt.
- Das Integral über den linken Halbkreis liefert die Zeitfunktion für $t ≥ 0$. Dieses umschließt alle Pole und ist mit dem Residuensatz in (relativ) einfacher Weise berechenbar, wie auf den nächsten Seiten gezeigt wird.
Formulierung des Residuensatzes
Es wird weiter vorausgesetzt, dass die Übertragungsfunktion $Y_{\rm L}(p)$ in Pol–Nullstellen–Form durch
- den konstanten Faktor $K$,
- die $Z$ Nullstellen $p_{{\rm o}i}$ $(i = 1$, ... , $Z)$ und
- die $N$ Polstellen $p_{{\rm x}i}$ $(i = 1$, ... , $N$)
dargestellt werden kann. Wir setzen zudem $Z < N$ voraus.
Die Anzahl der unterscheidbaren Pole bezeichnen wir mit $I$. Zur Bestimung von $I$ werden mehrfache Pole nur einfach gezählt. So gilt für die Skizze im letzten Abschnitt (unter Berücksichtigung des Poles bei $p=0$) aufgrund der doppelten Polstelle: $N = 5$ und $I = 4$.
$\text{Residuensatz:}$ Unter den genannten Voraussetzungen ergibt sich die Laplace–Rücktransformierte von $Y_{\rm L}(p)$ für Zeiten $t ≥ 0$ als die Summe von $I$ Eigenschwingungen der Pole, die man als die Residuen – abgekürzt mit „Res” – bezeichnet:
- $$y(t) = \sum_{i=1}^{I}{\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}_i}} \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p \hspace{0.05cm}t}\} \hspace{0.05cm} .$$
Da $Y_{\rm L}(p)$ nur für kausale Signale angebbar ist, gilt für negative Zeiten stets $y(t < 0) = 0$.
- Für einen Pol der Vielfachheit $l$ gilt allgemein:
- $${\rm Res} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{1}{(l-1)!}\cdot \frac{ {\rm d}^{\hspace{0.05cm}l-1} }{ {\rm d}p^{\hspace{0.05cm}l-1} }\hspace{0.15cm} \left \{Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i})^{\hspace{0.05cm}l}\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg \vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$
- Als Sonderfall ergibt sich daraus mit $l = 1$ für einen einfachen Pol:
- $${\rm Res} \bigg\vert_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{-0.7cm}\{Y_{\rm L}(p)\cdot {\rm e}^{p t}\}= Y_{\rm L}(p)\cdot (p - p_{ {\rm x}_i} )\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg \vert _{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x}_i} } \hspace{0.05cm} .$$
Auf den nächsten Seiten wird der Residuensatz anhand dreier ausführlicher Beispiele verdeutlicht, die mit den drei Konstellationen im $\text{Beispiel 3}$ im Kapitel „Laplace–Transformation” korrespondieren:
- Wir betrachten also wieder den Vierpol mit einer Induktivität $L = 25 \ \rm µH$ im Längszweig sowie im Querzweig die Serienschaltung aus einem Ohmschen Widerstand $R = 50 \ \rm Ω$ und einer Kapazität $C$.
- Für Letztere betrachten wir wieder drei verschiedene Werte, nämlich $C = 62.5 \ \rm nF$, $C = 8 \ \rm nF$ und $C = 40 \ \rm nF$.
- Vorausgesetzt ist stets $x(t) = δ(t) \; ⇒ \; X_{\rm L}(p) = 1$ ⇒ $Y_{\rm L}(p) = H_{\rm L}(p)$ ⇒ $y(t)$ ist gleich der Impulsantwort $h(t)$.
Aperiodisch abklingende Impulsantwort
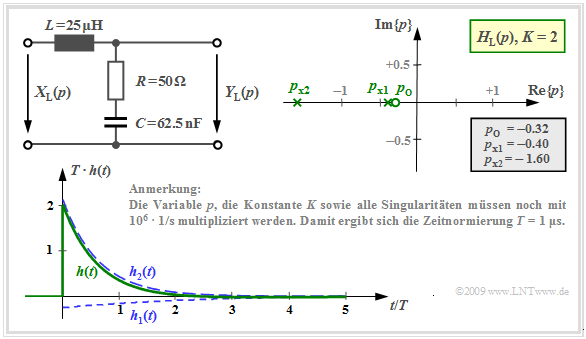
Mit der Kapazität $C = 62.5 \ \rm nF$ und den weiteren in der unteren Grafik angegebenen Zahlenwerten erhält man für die auf der Seite Pol–Nullstellen–Darstellung von Schaltungen berechnete $p$–Übertragungsfunktion:
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})}= 2 \cdot \frac {p + 0.32 } {(p +0.4)(p +1.6 )} \hspace{0.05cm} .$$
Beachten Sie bitte die Normierung von $p$, $K$ sowie aller Pole und Nullstellen mit dem Faktor ${\rm 10^6} · 1/\rm s$.
Die Impulsantwort setzt sich aus $I = N = 2$ Eigenschwingungen zusammen. Für $t < 0$ sind diese gleich Null.
- Das Residium des Pols bei $p_{{\rm x}1} =\ –0.4$ liefert folgende Zeitfunktion:
- $$h_1(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}1})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}$$
- $$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {p + 0.32 } {p +0.4}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.4}= - \frac {2 } {15}\cdot {\rm e}^{-0.4 \hspace{0.05cm} t} \hspace{0.05cm}. $$
- Für das Residium des zweiten Pols bei $p_{{\rm x}2} = \ –1.6$ gilt:
- $$h_2(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= H_{\rm L}(p)\cdot (p - p_{{\rm x}2})\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}$$
- $$\Rightarrow \hspace{0.3cm}h_2(t) = 2 \cdot \frac {p + 0.32 } {p +1.6}\cdot {\rm e}^{p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1.6}= \frac {32 } {15}\cdot {\rm e}^{-1.6 \hspace{0.05cm} t} \hspace{0.05cm}. $$
Die Grafik zeigt $h_1(t)$ und $h_2(t)$ sowie das Summensignal $h(t)$.
- Berücksichtigt ist auch hier der Normierungsfaktor $1/T = 10^6 · \rm 1/s$, so dass die Zeit auf $T = 1 \ \rm µ s$ normiert ist.
- Für $t =0$ ergibt sich $T \cdot h(t=0) = {32 }/ {15} -{2 }/ {15}= 2 \hspace{0.05cm}$.
- Für Zeiten $t > 2 \ \rm µ s$ ist die Impulsantwort negativ (wenn auch nur geringfügig und in der Grafik nur schwer zu erkennen).
Gedämpft oszillierende Impulsantwort
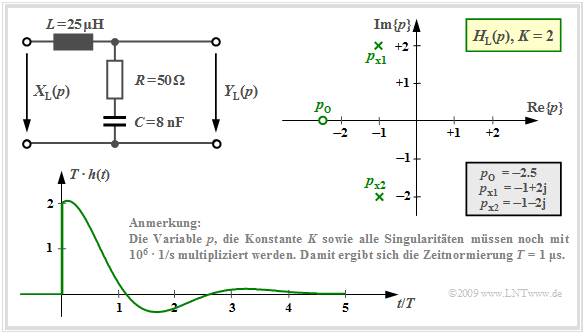
Die Bauelementewerte $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 8 \ \rm nF$ ergeben zwei konjugiert komplexe Pole bei $p_{{\rm x}1} = \ –1 + {\rm j} · 2$ und $p_{{\rm x}2} = \ –1 - {\rm j} · 2$.
- Die Nullstelle liegt bei $p_{\rm o} = \ –2.5$.
- Es gilt $K = 2$ und alle Zahlenwerte sind wieder mit dem Faktor $1/T$ zu multiplizieren $(T = 1\ \rm µ s$).
Wendet man den Residuensatz auf diese Konfiguration an, so erhält man:
- $$h_1(t) = K \cdot \frac {p_{\rm x 1} - p_{\rm o }} {p_{\rm x 1} - p_{\rm x 2}} \cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot \hspace{0.05cm}t} $$
- $$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {-1 + {\rm j}\cdot 2 +2.5} {(-1 + {\rm j}\cdot 2) - (-1 - {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}$$
- $$\Rightarrow \hspace{0.3cm}h_1(t) = 2 \cdot \frac {1.5 + {\rm j}\cdot 2} {{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 1} \cdot\hspace{0.05cm}t}= (1 - {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} ,$$
- $$ h_2(t) = K \cdot \frac {p_{\rm x 2} - p_{\rm o }} {p_{\rm x 2} - p_{\rm x 1}}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot \hspace{0.05cm}t} $$
- $$\Rightarrow \hspace{0.3cm} h_2(t) = 2 \cdot \frac {-1 - {\rm j}\cdot 2 +2.5} {(-1 - {\rm j}\cdot 2) - (-1 + {\rm j}\cdot 2)}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t} $$
- $$\Rightarrow \hspace{0.3cm}h_2(t) =2 \cdot \frac {1.5 - {\rm j}\cdot 2} {-{\rm j}\cdot 4}\cdot {\rm e}^{\hspace{0.05cm}p_{\rm x 2} \hspace{0.03cm}\cdot\hspace{0.05cm}t}= (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} $$
- $$\Rightarrow \hspace{0.3cm}h_2(t) = (1 + {\rm j}\cdot 0.75)\cdot {\rm e}^{-t}\cdot {\rm e}^{\hspace{0.03cm}-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 2t} \hspace{0.05cm} . $$
Mit dem Satz von Euler ergibt sich somit für das Summensignal:
- $$h(t) = h_1(t) + h_2(t)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}h(t) = {\rm e}^{-t}\cdot \big [ (1 - {\rm j}\cdot 0.75)\cdot (\cos() + {\rm j}\cdot \sin())+ + (1 + {\rm j}\cdot 0.75)\cdot (\cos() - {\rm j}\cdot \sin())\big ]$$
- $$\Rightarrow \hspace{0.3cm}h(t) ={\rm e}^{-t}\cdot \big [ 2\cdot \cos(2t) + 1.5 \cdot \sin(2t)\big ]\hspace{0.05cm} . $$
Die Grafik zeigt die nun mit ${\rm e}^{–t}$ gedämpft oszillierende Impulsantwort $h(t)$ für diese Pol–Nullstellen–Konfiguration.
Aperiodischer Grenzfall
Mit $R = 50 \ \rm Ω$, $L = 25 \ \rm µ H$ und $C = 40 \ \rm nF$ ergibt sich der so genannte aperiodische Grenzfall:
- $$H_{\rm L}(p)= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x })^2}= 2 \cdot \frac {p + 0.5 } {(p +1)^2} \hspace{0.05cm} .$$
Der Kapazitätswert $C = 40 \ \rm nF$ ist der kleinstmögliche Wert, für den sich gerade noch reelle Polstellen ergeben. Diese fallen zusammen, das heißt $p_{\rm x} = \ –1$ ist eine doppelte Polstelle. Die Zeitfunktion lautet somit entsprechend dem Residuensatz mit $l = 2$:
- $$h(t) = {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{-0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{p t}\}= \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{ {\rm x} })^2\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } = K \cdot \frac{ {\rm d} }{ {\rm d}p}\hspace{0.15cm}\left \{ (p - p_{ {\rm o} })\cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{ {\rm x} } } \hspace{0.05cm} .$$
Mit der Produktregel der Differentialrechnung ergibt sich daraus:
- $$h(t) = K \cdot \left [ {\rm e}^{p \hspace{0.05cm}t} + (p - p_{ {\rm o} })\cdot t \cdot {\rm e}^{p \hspace{0.05cm}t} \right ] \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-1} = {\rm e}^{-t}\cdot \left ( 2 - t \right) \hspace{0.05cm} .$$
- Die Grafik zeigt diese Impulsantwort als grüne Kurve in normierter Darstellung. Sie unterscheidet sich von derjenigen mit den beiden unterschiedlichen Polen bei $-0.4$ und $-1.6$ nur geringfügig.
- Das rot gezeichnete Signal $y(t) = 1 - {\rm e}^{-t} + t \cdot {\rm e}^{-t}$ ergibt sich, wenn am Eingang zusätzlich eine Sprungfunktion berücksichtigt wird.
Zur Berechnung der Sprungantwort $\sigma(t) = y(t)$ kann man alternativ
- bei der Residuenberechnung einen zusätzlichen Pol bei $p = 0$ (rot markiert) berücksichtigen, oder
- das Integral über die Impulsantwort $h(t)$ bilden.
Partialbruchzerlegung
Voraussetzung für die Anwendung des Residuensatzes ist, dass es weniger Nullstellen als Pole gibt ⇒ $Z$ muss stets kleiner als $N$ sein.
Gilt dagegen wie bei einem Hochpass $Z = N$, so
- ist der Grenzwert der Spektralfunktion für großes $p$ ungleich Null,
- beinhaltet das zugehörige Zeitsignal $y(t)$ auch einen Diracimpuls,
- versagt der Residuensatz und es ist eine Partialbruchzerlegung vorzunehmen.
Die Vorgehensweise soll beispielhaft für einen Hochpass erster Ordnung verdeutlicht werden.
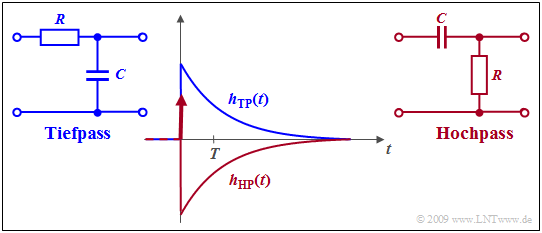
$\text{Beispiel 1:}$ Die $p$–Übertragungsfunktion eines RC–Hochpasses erster Ordnung kann durch Abspaltung einer Konstanten wie folgt umgewandelt werden:
- $$\frac{p}{p + RC} = 1- \frac{RC}{p + RC}\hspace{0.05cm} .$$
Damit lautet die Hochpass–Impulsantwort:
- $$h_{\rm HP}(t) = \delta(t) - h_{\rm TP}(t) \hspace{0.05cm} .$$
Die Grafik zeigt
- als rote Kurve die Hochpass–Impulsantwort $h_{\rm HP}(t)$,
- als blaue Kurve die Impulsantwort $h_{\rm TP}(t)$ des äquivalenten Tiefpasses.
Die Diracfunktion ist die Laplace–Transformierte des konstanten Wertes $1$, während die zweite, zu subtrahierende Funktion die Impulsantwort des äquivalenten Tiefpasses angibt, die durch den Residuensatz angebbar ist mit den Parametern
- $$Z = 0,\hspace{0.2cm} N =1,\hspace{0.2cm} K = RC.$$
Aufgaben zum Kapitel
Aufgabe 3.5: Schaltung mit R, L und C
Aufgabe 3.5Z: Anwendung des Residuensatzes
Aufgabe 3.6: Einschwingverhalten
Aufgabe 3.6Z: Zwei imaginäre Pole
Aufgabe 3.7: Hochpass-Impulsantwort
Aufgabe 3.7Z: Partialbruchzerlegung