Stochastische Signaltheorie/Momente einer diskreten Zufallsgröße: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
==Berechnung als Schar- bzw. Zeitmittelwert== | ==Berechnung als Schar- bzw. Zeitmittelwert== | ||
<br> | <br> | ||
| − | Die Wahrscheinlichkeiten | + | Die Wahrscheinlichkeiten und die relativen Häufigkeiten liefern weitreichende Informationen über eine diskrete Zufallsgröße. |
| + | |||
| + | Reduzierte Informationen erhält man durch die so genannten Momente $m_k$, wobei $k$ eine natürliche Zahl darstellt. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Zwei alternative Berechnungsmöglichkeiten:}$ | $\text{Zwei alternative Berechnungsmöglichkeiten:}$ | ||
| − | Unter der hier stillschweigend vorausgesetzten [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|Ergodizität]] gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten: | + | |
| − | *die '''Scharmittelung''' bzw. | + | Unter der hier stillschweigend vorausgesetzten Bedingung [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Ergodische_Zufallsprozesse|"Ergodizität"]] gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten: |
| − | :$$m_k = {\rm E} [z^k ] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E[\text{ ...} ]\hspace{-0.1cm}:} \hspace{0. | + | *die '''Scharmittelung''' bzw. "Erwartungswertbildung" ⇒ Mittelung über alle möglichen Werte $\{ z_\mu\}$ mit der Laufvariablen $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$: |
| − | *die '''Zeitmittelung''' über die Zufallsfolge $\langle z_ν\rangle$ mit der Laufvariablen $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$: | + | :$$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm Erwartungswert ;$$ |
| + | *die '''Zeitmittelung''' über die Zufallsfolge $\langle z_ν\rangle$ mit der Laufvariablen $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$: | ||
:$$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie\hspace{-0.1cm}:\hspace{0.1cm}Zeitmittelwert.$$}} | :$$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie\hspace{-0.1cm}:\hspace{0.1cm}Zeitmittelwert.$$}} | ||
Anzumerken ist: | Anzumerken ist: | ||
| − | *Beide Berechnungsarten führen | + | *Beide Berechnungsarten führen bei genügend großen Werten von $N$ zum gleichen asymptotischen Ergebnis. |
| − | *Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird. | + | *Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird. |
| − | ==Linearer Mittelwert | + | ==Moment erster Ordnung – Linearer Mittelwert – Gleichanteil== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ Mit $k = 1$ erhält man aus der allgemeinen Gleichung das Moment erster Ordnung ⇒ den '''linearen Mittelwert''' (englisch: "mean"): |
| − | Mit $k = 1$ erhält man aus der allgemeinen Gleichung | ||
:$$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$ | :$$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$ | ||
| − | Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte), während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt. In Zusammenhang mit Signalen wird diese Größe auch als der [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|Gleichanteil]] bezeichnet.}} | + | *Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte), |
| + | :während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt. | ||
| + | *In Zusammenhang mit Signalen wird diese Größe auch als der [[Signaldarstellung/Gleichsignal_-_Grenzfall_eines_periodischen_Signals|Gleichanteil]] bezeichnet.}} | ||
| − | [[Datei:P_ID49__Sto_T_2_2_S2_neu.png|right|frame|Gleichanteil $m_1$ eines Binärsignals]] | + | [[Datei:P_ID49__Sto_T_2_2_S2_neu.png|right|frame|Gleichanteil $m_1$ eines Binärsignals]] |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ | + | $\text{Beispiel 1:}$ Ein Binärsignal $x(t)$ mit den beiden möglichen Amplitudenwerten |
| − | Ein Binärsignal $x(t)$ mit den beiden möglichen Amplitudenwerten | + | *$1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$, |
| − | *$1\hspace{0.03cm}\rm V$ (für das Symbol $\rm L$ | + | *$3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$ |
| − | *$3\hspace{0.03cm}\rm V$ (für das Symbol $\rm H$ | ||
| − | sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ besitzt den linearen Mittelwert (Gleichanteil ) | + | |
| + | sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ besitzt den linearen Mittelwert (Gleichanteil ) | ||
:$$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$ | :$$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$ | ||
Dieser ist in der Grafik als rote Linie eingezeichnet. | Dieser ist in der Grafik als rote Linie eingezeichnet. | ||
| − | + | ||
| − | Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N = 12$ Signalwerte, so erhält man einen etwas kleineren Wert: | + | Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N = 12$ Signalwerte, so erhält man einen etwas kleineren Wert: |
:$$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$ | :$$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$ | ||
| − | Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ durch die entsprechenden Häufigkeiten $h_{\rm L} = 4/12$ und $h_{\rm H} = 8/12$ ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als $10\%$. | + | Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ durch die entsprechenden Häufigkeiten $h_{\rm L} = 4/12$ und $h_{\rm H} = 8/12$ ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als $10\%$. |
| + | $\text{Hinweis zu unserer (zugegebenermaßen etwas ungewöhnlicher) Nomenklatur:}$ | ||
| − | + | Wir bezeichnen hier Binärsymbole wie in der Schaltungstechnik mit $\rm L$ ("Low") und $\rm H$ ("High"), um Verwechslungen zu vermeiden. | |
| − | + | *In der Codierungstheorie wird sinnvollerweise $\{ \text{L, H}\}$ auf $\{0, 1\}$ abgebildet, um die Möglichkeiten der Modulo-Algebra nutzen zu können. | |
| − | Wir bezeichnen hier Binärsymbole wie in der Schaltungstechnik mit $\rm L$ (Low) und $\rm H$ (High), um Verwechslungen zu vermeiden. | + | *Zur Beschreibung der Modulation mit bipolaren (antipodalen) Signalen wählt man dagegen besser die Zuordnung $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$. |
| − | *In der Codierungstheorie wird sinnvollerweise $\{ \text{L, H}\}$ auf $\{0, 1\}$ abgebildet, um die Möglichkeiten der Modulo-Algebra nutzen zu können. | ||
| − | *Zur Beschreibung der Modulation mit bipolaren (antipodalen) Signalen wählt man dagegen besser die Zuordnung $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$. | ||
}} | }} | ||
| − | == | + | ==Moment zweiter Ordnung – Leistung – Varianz – Streuung== |
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definitionen:}$ | $\text{Definitionen:}$ | ||
| − | Analog zum linearen Mittelwert erhält man mit $k = 2$ | + | *Analog zum linearen Mittelwert erhält man mit $k = 2$ das '''Moment zweiter Ordnung''' (englisch: "second order moment"): |
:$$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$ | :$$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$ | ||
| − | Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die '''Varianz''' $σ^2$ bestimmt werden ( | + | *Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die '''Varianz''' (englisch: "variance") $σ^2$ bestimmt werden ("Satz von Steiner"): |
:$$\sigma^2=m_2-m_1^2.$$ | :$$\sigma^2=m_2-m_1^2.$$ | ||
| − | + | *Die '''Streuung''' $σ$ ist die Quadratwurzel der Varianz; manchmal wird diese Größe auch "Standardabweichung" (englisch: "standard deviation") genannt: | |
:$$\sigma=\sqrt{m_2-m_1^2}.$$}} | :$$\sigma=\sqrt{m_2-m_1^2}.$$}} | ||
| − | + | $\text{Hinweise zu den Einheiten:}$ | |
| − | + | #Bei einem Zufallssignal $x(t)$ gibt $m_2$ die gesamte Leistung (Gleichleistung plus Wechselleitung) an, bezogen auf den Widerstand $1 \hspace{0.03cm} Ω$. | |
| − | + | #Beschreibt $x(t)$ einen Spannungsverlauf, so besitzt dementsprechend $m_2$ die Einheit ${\rm V}^2$ und der Effektivwert (englisch: "root mean square") $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm V}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2/R$ und besitzt dementsprechend die Einheit $\rm V^2/(V/A) = W$. | |
| − | + | #Beschreibt $x(t)$ einen Stromverlauf, so hat $m_2$ die Einheit ${\rm A}^2$ und der Effektivwert $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm A}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2\cdot R$ und besitzt dementsprechend die Einheit $\rm A^2 \cdot(V/A) = W$. | |
| − | + | #Nur im Sonderfall $m_1=0$ ist die Varianz $σ^2=m_2$. Dann stimmt auch die Standardabweichung $σ$ mit dem Effektivwert $x_{\rm eff}$ überein. | |
| − | Das Lernvideo [[Momentenberechnung bei diskreten Zufallsgrößen (Lernvideo)|Momentenberechnung bei diskreten Zufallsgrößen]] verdeutlicht die definierten Größen am Beispiel eines Digitalsignals. | + | Das Lernvideo [[Momentenberechnung bei diskreten Zufallsgrößen (Lernvideo)|Momentenberechnung bei diskreten Zufallsgrößen]] verdeutlicht die definierten Größen am Beispiel eines Digitalsignals. |
| − | |||
[[Datei:P_ID456__Sto_T_2_2_S3_neu.png | right|frame|Standardabweichung eines Binärsignals]] | [[Datei:P_ID456__Sto_T_2_2_S3_neu.png | right|frame|Standardabweichung eines Binärsignals]] | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 2:}$ | $\text{Beispiel 2:}$ | ||
| − | + | Bei einem Binärsignal $x(t)$ mit den Amplitudenwerten | |
| − | *$1\hspace{0. | + | *$1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$, |
| − | *$3\hspace{0. | + | *$3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ ergibt sich für das zweite Moment: | ||
| + | :$$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$ | ||
| − | + | Der Effektivwert $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ ist unabhängig vom Bezugswiderstand $R$ im Gegensatz zur Gesamtleistung. Für diese ergibt sich mit $R=1 \hspace{0.1cm} Ω$ der Wert $P=7.4 \hspace{0.1cm}{\rm W}$, mit $R=50 \hspace{0.1cm} Ω$ dagegen nur $P=0.148 \hspace{0.1cm}{\rm W}$. | |
| − | + | ||
| − | + | Mit dem Gleichanteil $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($siehe [[Stochastische_Signaltheorie/Momente_einer_diskreten_Zufallsgröße#Linearer_Mittelwert_-_Gleichanteil|$\text{Beispiel 1})$]] folgt daraus für | |
| − | + | *die Varianz $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$, | |
| + | *die Standardabweichung (Streuung) $σ = 0.8 \hspace{0.05cm} \rm V$. | ||
| − | + | Die gleiche Varianz $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ und die gleiche Standardabweichung $σ = 0.8 \hspace{0.05cm} \rm V$ ergeben sich für die Amplituden $0\hspace{0.05cm}\rm V$ $($für das Symbol $\rm L)$ und $2\hspace{0.05cm}\rm V$ $($für das Symbol $\rm H)$, vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ und $p_{\rm H} = 0.8$ bleiben gleich. Nur der Gleichanteil und die Gesamtleistung ändern sich: | |
| − | :$$m_1 = | + | :$$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$ |
| + | :$$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$}} | ||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
Aktuelle Version vom 18. Februar 2022, 14:26 Uhr
Inhaltsverzeichnis
Berechnung als Schar- bzw. Zeitmittelwert
Die Wahrscheinlichkeiten und die relativen Häufigkeiten liefern weitreichende Informationen über eine diskrete Zufallsgröße.
Reduzierte Informationen erhält man durch die so genannten Momente $m_k$, wobei $k$ eine natürliche Zahl darstellt.
$\text{Zwei alternative Berechnungsmöglichkeiten:}$
Unter der hier stillschweigend vorausgesetzten Bedingung "Ergodizität" gibt es für das Moment $k$-ter Ordnung zwei unterschiedliche Berechnungsmöglichkeiten:
- die Scharmittelung bzw. "Erwartungswertbildung" ⇒ Mittelung über alle möglichen Werte $\{ z_\mu\}$ mit der Laufvariablen $\mu = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , M$:
- $$m_k = {\rm E} \big[z^k \big] = \sum_{\mu = 1}^{M}p_\mu \cdot z_\mu^k \hspace{2cm} \rm mit \hspace{0.1cm} {\rm E\big[\text{ ...} \big]\hspace{-0.1cm}:} \hspace{0.3cm} \rm Erwartungswert ;$$
- die Zeitmittelung über die Zufallsfolge $\langle z_ν\rangle$ mit der Laufvariablen $ν = 1 , \hspace{0.1cm}\text{ ...} \hspace{0.1cm} , N$:
- $$m_k=\overline{z_\nu^k}=\hspace{0.01cm}\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=\rm 1}^{\it N}z_\nu^k\hspace{1.7cm}\rm mit\hspace{0.1cm}\ddot{u}berstreichender\hspace{0.1cm}Linie\hspace{-0.1cm}:\hspace{0.1cm}Zeitmittelwert.$$
Anzumerken ist:
- Beide Berechnungsarten führen bei genügend großen Werten von $N$ zum gleichen asymptotischen Ergebnis.
- Bei endlichem $N$ ergibt sich ein vergleichbarer Fehler, als wenn die Wahrscheinlichkeit durch die relative Häufigkeit angenähert wird.
Moment erster Ordnung – Linearer Mittelwert – Gleichanteil
$\text{Definition:}$ Mit $k = 1$ erhält man aus der allgemeinen Gleichung das Moment erster Ordnung ⇒ den linearen Mittelwert (englisch: "mean"):
- $$m_1 =\sum_{\mu=1}^{M}p_\mu\cdot z_\mu =\lim_{N\to\infty}\frac{1}{N}\sum_{\nu=1}^{N}z_\nu.$$
- Der linke Teil dieser Gleichung beschreibt die Scharmittelung (über alle möglichen Werte),
- während die rechte Gleichung die Bestimmung als Zeitmittelwert angibt.
- In Zusammenhang mit Signalen wird diese Größe auch als der Gleichanteil bezeichnet.
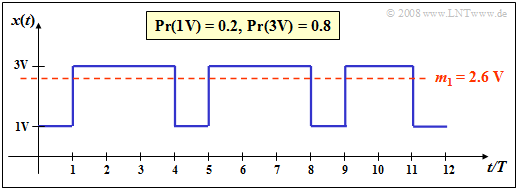
$\text{Beispiel 1:}$ Ein Binärsignal $x(t)$ mit den beiden möglichen Amplitudenwerten
- $1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$
sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ besitzt den linearen Mittelwert (Gleichanteil )
- $$m_1 = 0.2 \cdot 1\,{\rm V}+ 0.8 \cdot 3\,{\rm V}= 2.6 \,{\rm V}. $$
Dieser ist in der Grafik als rote Linie eingezeichnet.
Bestimmt man diese Kenngröße durch Zeitmittelung über die dargestellten $N = 12$ Signalwerte, so erhält man einen etwas kleineren Wert:
- $$m_1\hspace{0.01cm}' = 4/12 \cdot 1\,{\rm V}+ 8/12 \cdot 3\,{\rm V}= 2.33 \,{\rm V}. $$
Hier wurden die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ durch die entsprechenden Häufigkeiten $h_{\rm L} = 4/12$ und $h_{\rm H} = 8/12$ ersetzt. Der relative Fehler aufgrund der unzureichenden Folgenlänge $N$ ist im Beispiel größer als $10\%$.
$\text{Hinweis zu unserer (zugegebenermaßen etwas ungewöhnlicher) Nomenklatur:}$
Wir bezeichnen hier Binärsymbole wie in der Schaltungstechnik mit $\rm L$ ("Low") und $\rm H$ ("High"), um Verwechslungen zu vermeiden.
- In der Codierungstheorie wird sinnvollerweise $\{ \text{L, H}\}$ auf $\{0, 1\}$ abgebildet, um die Möglichkeiten der Modulo-Algebra nutzen zu können.
- Zur Beschreibung der Modulation mit bipolaren (antipodalen) Signalen wählt man dagegen besser die Zuordnung $\{ \text{L, H}\}$ ⇔ $ \{-1, +1\}$.
Moment zweiter Ordnung – Leistung – Varianz – Streuung
$\text{Definitionen:}$
- Analog zum linearen Mittelwert erhält man mit $k = 2$ das Moment zweiter Ordnung (englisch: "second order moment"):
- $$m_2 =\sum_{\mu=\rm 1}^{\it M}p_\mu\cdot z_\mu^2 =\lim_{N\to\infty}\frac{\rm 1}{\it N}\sum_{\nu=\rm 1}^{\it N}z_\nu^2.$$
- Zusammen mit dem Gleichanteil $m_1$ kann daraus als weitere Kenngröße die Varianz (englisch: "variance") $σ^2$ bestimmt werden ("Satz von Steiner"):
- $$\sigma^2=m_2-m_1^2.$$
- Die Streuung $σ$ ist die Quadratwurzel der Varianz; manchmal wird diese Größe auch "Standardabweichung" (englisch: "standard deviation") genannt:
- $$\sigma=\sqrt{m_2-m_1^2}.$$
$\text{Hinweise zu den Einheiten:}$
- Bei einem Zufallssignal $x(t)$ gibt $m_2$ die gesamte Leistung (Gleichleistung plus Wechselleitung) an, bezogen auf den Widerstand $1 \hspace{0.03cm} Ω$.
- Beschreibt $x(t)$ einen Spannungsverlauf, so besitzt dementsprechend $m_2$ die Einheit ${\rm V}^2$ und der Effektivwert (englisch: "root mean square") $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm V}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2/R$ und besitzt dementsprechend die Einheit $\rm V^2/(V/A) = W$.
- Beschreibt $x(t)$ einen Stromverlauf, so hat $m_2$ die Einheit ${\rm A}^2$ und der Effektivwert $x_{\rm eff}=\sqrt{m_2}$ die Einheit ${\rm A}$. Die Gesamtleistung für beliebigen Bezugswiderstand $R$ berechnet sich zu $P=m_2\cdot R$ und besitzt dementsprechend die Einheit $\rm A^2 \cdot(V/A) = W$.
- Nur im Sonderfall $m_1=0$ ist die Varianz $σ^2=m_2$. Dann stimmt auch die Standardabweichung $σ$ mit dem Effektivwert $x_{\rm eff}$ überein.
Das Lernvideo Momentenberechnung bei diskreten Zufallsgrößen verdeutlicht die definierten Größen am Beispiel eines Digitalsignals.
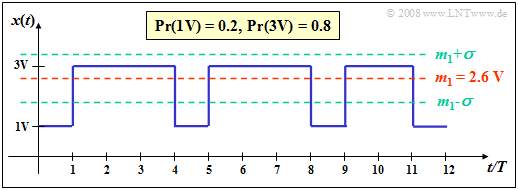
$\text{Beispiel 2:}$ Bei einem Binärsignal $x(t)$ mit den Amplitudenwerten
- $1\hspace{0.03cm}\rm V$ $($für das Symbol $\rm L)$,
- $3\hspace{0.03cm}\rm V$ $($für das Symbol $\rm H)$
sowie den Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ bzw. $p_{\rm H} = 0.8$ ergibt sich für das zweite Moment:
- $$m_2 = 0.2 \cdot (1\,{\rm V})^2+ 0.8 \cdot (3\,{\rm V})^2 = 7.4 \hspace{0.1cm}{\rm V}^2,$$
Der Effektivwert $x_{\rm eff}=\sqrt{m_2}=2.72\,{\rm V}$ ist unabhängig vom Bezugswiderstand $R$ im Gegensatz zur Gesamtleistung. Für diese ergibt sich mit $R=1 \hspace{0.1cm} Ω$ der Wert $P=7.4 \hspace{0.1cm}{\rm W}$, mit $R=50 \hspace{0.1cm} Ω$ dagegen nur $P=0.148 \hspace{0.1cm}{\rm W}$.
Mit dem Gleichanteil $m_1 = 2.6 \hspace{0.05cm}\rm V$ $($siehe $\text{Beispiel 1})$ folgt daraus für
- die Varianz $ σ^2 = 7.4 \hspace{0.05cm}{\rm V}^2 - \big [2.6 \hspace{0.05cm}\rm V\big ]^2 = 0.64\hspace{0.05cm} {\rm V}^2$,
- die Standardabweichung (Streuung) $σ = 0.8 \hspace{0.05cm} \rm V$.
Die gleiche Varianz $ σ^2 = 0.64\hspace{0.05cm} {\rm V}^2$ und die gleiche Standardabweichung $σ = 0.8 \hspace{0.05cm} \rm V$ ergeben sich für die Amplituden $0\hspace{0.05cm}\rm V$ $($für das Symbol $\rm L)$ und $2\hspace{0.05cm}\rm V$ $($für das Symbol $\rm H)$, vorausgesetzt, die Auftrittswahrscheinlichkeiten $p_{\rm L} = 0.2$ und $p_{\rm H} = 0.8$ bleiben gleich. Nur der Gleichanteil und die Gesamtleistung ändern sich:
- $$m_1 = 1.6 \hspace{0.05cm}{\rm V}, $$
- $$P = {m_1}^2 +\sigma^2 = 3.2 \hspace{0.05cm}{\rm V}^2.$$
Aufgaben zum Kapitel
Aufgabe 2.2: Mehrstufensignale
Aufgabe 2.2Z: Diskrete Zufallsgrößen