Aufgaben:Aufgabe 2.1Z: Zur äquivalenten Bitrate: Unterschied zwischen den Versionen
Aus LNTwww
K (Textersetzung - „*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.“ durch „ “) |
|||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
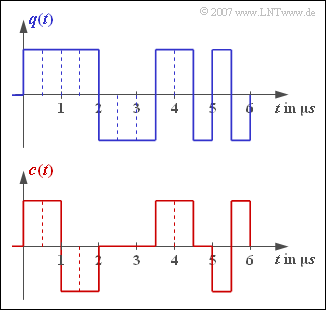
[[Datei:P_ID1309__Dig_Z_2_1.png|right|frame|Quellensignal (oben) und Codersignal (unten)]] | [[Datei:P_ID1309__Dig_Z_2_1.png|right|frame|Quellensignal (oben) und Codersignal (unten)]] | ||
| − | Die obere Darstellung zeigt das Quellensignal $q(t)$ einer redundanzfreien Binärquelle mit Bitdauer $T_{q}$ und Bitrate $R_{q}$. Die beiden Signalparameter $T_{q}$ und $R_{q}$ können der Skizze entnommen werden. | + | Die obere Darstellung zeigt das Quellensignal $q(t)$ einer redundanzfreien Binärquelle mit Bitdauer $T_{q}$ und Bitrate $R_{q}$. Die beiden Signalparameter $T_{q}$ und $R_{q}$ können der Skizze entnommen werden. |
| − | Dieses Binärsignal wird symbolweise codiert und ergibt das unten gezeichnete Codersignal $c(t)$. Alle möglichen Codesymbole kommen in dem dargestellten Signalausschnitt der Dauer $6 \ \rm | + | *Dieses Binärsignal wird symbolweise codiert und ergibt das unten gezeichnete Codersignal $c(t)$. |
| − | Mit der Stufenzahl $M_{c}$ und der Symboldauer $T_{c}$ kann man die äquivalente Bitrate | + | *Alle möglichen Codesymbole kommen in dem dargestellten Signalausschnitt der Dauer $6 \ \rm µ s$ vor. |
| + | *Mit der Stufenzahl $M_{c}$ und der Symboldauer $T_{c}$ kann man die äquivalente Bitrate des Codersignals angeben: | ||
:$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$ | :$$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$ | ||
Daraus erhält man die relative Redundanz des Codes, wenn man wie hier davon ausgeht, dass die Quelle selbst redundanzfrei ist: | Daraus erhält man die relative Redundanz des Codes, wenn man wie hier davon ausgeht, dass die Quelle selbst redundanzfrei ist: | ||
| Zeile 16: | Zeile 17: | ||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Grundlagen_der_codierten_Übertragung|Grundlagen der codierten Übertragung]]. | + | *Die Aufgabe gehört zum Kapitel [[Digitalsignalübertragung/Grundlagen_der_codierten_Übertragung|"Grundlagen der codierten Übertragung"]]. |
| − | *Bei dem hier betrachteten Übertragungscode handelt es sich um den Bipolarcode zweiter Ordnung, was jedoch für die Lösung dieser Aufgabe nicht von Bedeutung ist. | + | *Bei dem hier betrachteten Übertragungscode handelt es sich um den Bipolarcode zweiter Ordnung, was jedoch für die Lösung dieser Aufgabe nicht von Bedeutung ist. |
| Zeile 27: | Zeile 28: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie Bitdauer $(T_{q})$ und Bitrate $(R_{q})$ der Quelle an | + | {Geben Sie die Bitdauer $(T_{q})$ und die Bitrate $(R_{q})$ der Quelle an. |
|type="{}"} | |type="{}"} | ||
| − | $T_{q} \ = \ $ { 0.5 3% } $\ \rm | + | $T_{q} \ = \ $ { 0.5 3% } $\ \rm µ s $ |
$R_{q} \ = \ $ { 2 3% } $\ \rm Mbit/s $ | $R_{q} \ = \ $ { 2 3% } $\ \rm Mbit/s $ | ||
| − | {Wie groß sind Symboldauer $(T_{c})$ und Stufenzahl $(M_{c})$ des Codersignals? | + | {Wie groß sind Symboldauer $(T_{c})$ und Stufenzahl $(M_{c})$ des Codersignals? |
|type="{}"} | |type="{}"} | ||
| − | $T_{c} \ = \ $ { 0.5 3% } $\ \rm | + | $T_{c} \ = \ $ { 0.5 3% } $\ \rm µ s $ |
$M_{c} \ = \ $ { 3 3% } | $M_{c} \ = \ $ { 3 3% } | ||
| − | {Wie groß ist die äquivalente Bitrate $R_{c}$ des Codersignals? | + | {Wie groß ist die äquivalente Bitrate $R_{c}$ des Codersignals? |
|type="{}"} | |type="{}"} | ||
$R_{c} \ = \ $ { 3.17 3% } $\ \rm Mbit/s $ | $R_{c} \ = \ $ { 3.17 3% } $\ \rm Mbit/s $ | ||
| Zeile 50: | Zeile 51: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Bitdauer $T_{q} = \underline{0.5\ \ | + | '''(1)''' Die Bitdauer $T_{q} = \underline{0.5\ \rm µ s}$ kann der Grafik entnommen werden. |
| + | *Da die Quelle binär und redundanzfrei ist, gilt für die Bitrate der Quelle: | ||
| + | :$$R_{q}= 1/T_{q}\ \underline{= 2\ \rm Mbit/s}.$$ | ||
| − | |||
| − | '''(3)''' Die Symbolrate des Codersignals beträgt $2 \cdot 10^{6}$ Ternärsymbole pro Sekunde. Für die äquivalente Bitrate gilt | + | '''(2)''' Bei symbolweiser Codierung gilt stets $T_{c} = T_{q}$. |
| + | *Im vorliegenden Beispiel ist somit auch $T_{c}\ \underline{ = 0.5\ \rm µ s}$. | ||
| + | *Die Stufenzahl $M_{c}\ \underline{ = 3}$ kann aus der unteren Skizze abgelesen werden. | ||
| + | |||
| + | |||
| + | '''(3)''' Die Symbolrate des Codersignals beträgt $2 \cdot 10^{6}$ Ternärsymbole pro Sekunde. | ||
| + | *Für die äquivalente Bitrate gilt: | ||
:$$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$ | :$$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$ | ||
| + | |||
'''(4)''' Für die relative Coderedundanz gilt bei redundanzfreier Quelle allgemein: | '''(4)''' Für die relative Coderedundanz gilt bei redundanzfreier Quelle allgemein: | ||
:$$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$ | :$$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$ | ||
| − | Beim hier betrachteten Biploarcodes 2. Ordnung mit den Parametern $T_{c} = T_{q}$ und $M_{c} = 3$ gilt weiter: | + | *Beim hier betrachteten Biploarcodes 2. Ordnung mit den Parametern $T_{c} = T_{q}$ und $M_{c} = 3$ gilt weiter: |
:$$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$ | :$$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$ | ||
Aktuelle Version vom 13. Mai 2022, 17:10 Uhr
Die obere Darstellung zeigt das Quellensignal $q(t)$ einer redundanzfreien Binärquelle mit Bitdauer $T_{q}$ und Bitrate $R_{q}$. Die beiden Signalparameter $T_{q}$ und $R_{q}$ können der Skizze entnommen werden.
- Dieses Binärsignal wird symbolweise codiert und ergibt das unten gezeichnete Codersignal $c(t)$.
- Alle möglichen Codesymbole kommen in dem dargestellten Signalausschnitt der Dauer $6 \ \rm µ s$ vor.
- Mit der Stufenzahl $M_{c}$ und der Symboldauer $T_{c}$ kann man die äquivalente Bitrate des Codersignals angeben:
- $$R_c = \frac{{\rm log_2} (M_c)}{T_c} \hspace{0.05cm}.$$
Daraus erhält man die relative Redundanz des Codes, wenn man wie hier davon ausgeht, dass die Quelle selbst redundanzfrei ist:
- $$r_c = \frac{R_c - R_q}{R_c}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel "Grundlagen der codierten Übertragung".
- Bei dem hier betrachteten Übertragungscode handelt es sich um den Bipolarcode zweiter Ordnung, was jedoch für die Lösung dieser Aufgabe nicht von Bedeutung ist.
Fragebogen
Musterlösung
(1) Die Bitdauer $T_{q} = \underline{0.5\ \rm µ s}$ kann der Grafik entnommen werden.
- Da die Quelle binär und redundanzfrei ist, gilt für die Bitrate der Quelle:
- $$R_{q}= 1/T_{q}\ \underline{= 2\ \rm Mbit/s}.$$
(2) Bei symbolweiser Codierung gilt stets $T_{c} = T_{q}$.
- Im vorliegenden Beispiel ist somit auch $T_{c}\ \underline{ = 0.5\ \rm µ s}$.
- Die Stufenzahl $M_{c}\ \underline{ = 3}$ kann aus der unteren Skizze abgelesen werden.
(3) Die Symbolrate des Codersignals beträgt $2 \cdot 10^{6}$ Ternärsymbole pro Sekunde.
- Für die äquivalente Bitrate gilt:
- $$R_c = \frac{{\rm log_2} (M_c)}{T_c} = \frac{{\rm log_2}(3)}{0.5\,\,{\rm \mu s}} = \frac{{\rm lg} (3)}{{\rm lg} (2) \cdot 0.5\,\,{\rm \mu s}}= \frac{1.585\,\,{\rm (bit)}}{0.5\,\,{\rm \mu s}}\hspace{0.15cm} \underline {\approx 3.17\,\,{\rm Mbit/s}} \hspace{0.05cm}.$$
(4) Für die relative Coderedundanz gilt bei redundanzfreier Quelle allgemein:
- $$ r_c = \frac{R_c - R_q}{R_c} = 1- \frac{R_q}{R_c}= 1- \frac{T_c}{T_q \cdot {\rm log_2} (M_c)}\hspace{0.05cm}.$$
- Beim hier betrachteten Biploarcodes 2. Ordnung mit den Parametern $T_{c} = T_{q}$ und $M_{c} = 3$ gilt weiter:
- $$r_c = 1- \frac{1}{{\rm log_2} (3)}\hspace{0.15cm}\underline {\approx 36.9 \% }\hspace{0.05cm}.$$