Aufgaben:Aufgabe 2.3Z: Zur LZ77-Codierung

• Zurück zum Buch

Sliding–Window mit  $G = 4$  und  $G = 5$
(gültig für „LZ77”)

In der  Aufgabe 2.3  sollten Sie  "BARBARA–BAR"  (String der Länge  $11$, vier verschiedene Zeichen)  mit dem LZ78–Algorithmus komprimieren. 

In dieser Aufgabe verwenden wir den gleichen Text zur Demonstration der LZ77–Komprimierung.  Anzumerken ist:

• Während beim Nachfolger „LZ78” sukzessive ein globales Wörterbuch aufgebaut wird, verwendet „LZ77” ein lokales Wörterbuch.
• Das LZ77–Verfahren arbeitet mit einem  „Sliding Window”, das schrittweise über den Eingabetext verschoben wird.
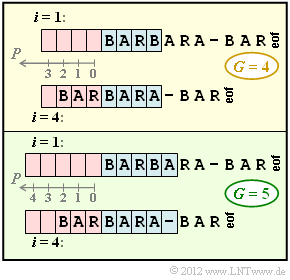
• Dieses „gleitende Fenster” ist unterteilt in den  „Vorschaupuffer”  (in der Grafik blau hinterlegt) und den  „Suchpuffer”  (rote Hinterlegung).  Beide Puffer haben je eine Größe von  $G$  Speicherplätzen.
• Jeder Codierschritt  $i$  wird durch ein Zahlentriple  $(P,\ L,\ Z)$  charakterisiert.  Hierbei sind  $P$  und  $L$  Integergrößen und  $Z$  ein Character.  Übertragen werden die Binärdarstellungen von  $P$,  $L$  und  $Z$.
• Nach der Übertragung wird das  „Sliding Window”  um eine oder mehrere Positionen nach rechts verschoben und es beginnt der nächste Codierschritt  $i + 1$.

Die obere Grafik zeigt die Anfangsbelegung mit der Puffergröße  $G = 4$  zu den Zeitpunkten  $i = 1$  sowie  $i = 4$.

• Zum Zeitpunkt  $i = 1$  ist der Suchpuffer leer, so dass die Coderausgabe  $(0, 0,$ B$)$  lautet.
• Nach der Verschiebung um eine Position beinhaltet der Suchpuffer ein  B, aber keinen String, der mit  A  anfängt.  Das zweite Zahlentriple ist somit  $(0, 0,$ A$)$.
• Die Ausgabe für  $i = 3$  lautet  $(0, 0,$ R$)$, da im Suchpuffer auch jetzt keine mit  R  beginnende Zeichenfolge zu finden ist.

Die Momentaufnahme zum Zeitpunkt  $i = 4$  ist ebenfalls in der Grafik angegeben.  Gesucht ist nun die Zeichenfolge im Suchpuffer, die mit dem Vorschautext  BARA  am besten übereinstimmt.  Übertragen wird wieder ein Zahlentriple  $(P,\ L,\ Z)$, aber nun mit folgender Bedeutung:

• $P$  gibt die Position im (roten) Suchpuffer an, bei der die Übereinstimmung beginnt.  Die  $P$–Werte der einzelnen Speicherplätze kann man der Grafik entnehmen.
• $L$  bezeichnet die Anzahl der Zeichen im Suchpuffer, die beginnend bei  $P$  mit dem aktuellen String im Vorschaupuffer übereinstimmen.
• $Z$  bezeichnet schließlich das erste Zeichen im Vorschaupuffer, das sich vom gefundenen Übereinstimmungs–String im Suchpuffer unterscheidet.

Je größer der LZ77–Parameter  $G$  ist, um so leichter findet man eine möglichst lange Übereinstimmung.  In der Teilaufgabe  (4)  werden Sie feststellen, dass die LZ77–Codierung mit  $G = 5$  ein besseres Ergebnis liefert als diejenige mit  $G = 4$.

• Aufgrund der späteren Binärdarstellung von  $P$ wird  man allerdings  $G$  stets als Zweierpotenz wählen, so dass  $G$  mit  $\log_2 \ P$  Bit darstellbar ist 
  $(G = 8$   ⇒   dreistellige Binärzahl  $P)$.
• Das heißt, ein  „Sliding Window”  mit  $G = 5$  hat eher einen geringen Praxisbezug.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Komprimierung nach Lempel, Ziv und Welch.
• Insbesondere wird auf die Seite  LZ77 – die Grundform der Lempel-Ziv-Algorithmen  Bezug genommen.
• Die Originalliteratur  [LZ77]  zu diesem Verfahren lautet:
  Ziv, J.; Lempel, A.:  A Universal Algorithm for Sequential Data Compression.  In: IEEE Transactions on Information Theory, no. 3, vol. 23, 1977, p. 337–343.

• Die  Aufgabe 2.3  sowie die  Aufgabe 2.4  behandeln andere Lempel–Ziv-Verfahren in ähnlicher Weise.

Fragebogen

1

Wie lautet die LZ77–Ausgabe mit  $G = 4$  beim Schritt  $i = 4$?

	$(0, 0,$ B$)$,
	$(2, 1,$ A$)$,
	$(2, 3,$ A$)$.

2

Welche Aussage gilt für die gleiche Puffergröße  $G = 4$  beim Schritt  $i = 5$?

	Im Suchpuffer steht  BARA.
	Im Vorschaupuffer steht  –BAR.
	Die Ausgabe lautet  $(0, 0,$ A$)$.

3

Nach welchem Schritt  $i_{\rm Ende}$  ist die Codierung mit  $G = 4$  beendet?

$i_{\rm Ende} \ = \ $

4

Nun gelte  $G = 5$.  Nach welchem Schritt  $i_{\rm Ende}$  ist nun die Codierung beendet?

$i_{\rm Ende} \ = \ $

5

Welche Vorteile hat LZ78 gegenüber LZ77 bei „sehr großen” Dateien?

	Man findet häufiger bereits abgelegte Phrasen im Wörterbuch.
	Pro Codierschritt müssen weniger Bit übertragen werden.

Musterlösung

Musterlösung

Beispiel zum LZ77–Algorithmus mit  $G = 4$

(1)  Richtig ist der Lösungsvorschlag 3.

• Im Vorschaupuffer steht zum betrachteten Zeitpunkt  $i = 4$  die Zeichenfolge  BARA.
• Im Suchpuffer steht in den letzten drei Stellen  BAR:

$$P = 2\hspace{0.05cm},\hspace{0.2cm}L = 3\hspace{0.05cm},\hspace{0.2cm}Z = \boldsymbol{\rm A}\hspace{0.05cm}.$$

(2)  Richtig sind die beiden ersten Lösungsvorschläge:

• Der Bindestrich findet sich zum Zeitpunkt  $i = 5$  nicht im Suchpuffer.
• Ausgegeben wird  $(0, 0,$ –$)$.

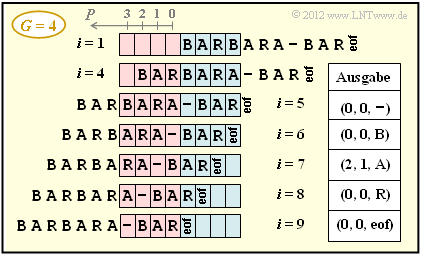
(3)  Die obere Grafik zeigt das  „Sliding–Window”  und die Coderausgabe zu den Zeiten  $i>5$.

• Nach  $i = 9$  Codierschritten ist der Codiervorgang unter Berücksichtigung von  "eof"  beendet   ⇒   $\underline{i_{\rm Ende} = 9}$.

Beispiel zum LZ77–Algorithmus mit  $G = 5$

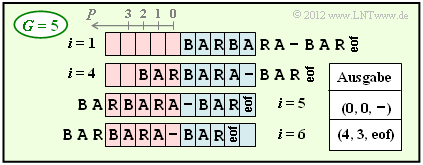
(4)  Bei größerer Puffergröße  $(G = 5$  anstelle von  $G = 4)$  ist die Codierung schon nach dem 6. Codierschritt abgeschlossen   ⇒   $\underline{i_{\rm Ende} = 6}$.

• Ein Vergleich der beiden Grafiken zeigt, dass sich für  $G = 5$  gegenüber  $G = 4$  bis einschließlich  $i = 5$  nichts ändert.
• Aufgrund des größeren Puffers lässt sich aber nun  BAR  gemeinsam mit  eof  (end-of-file) in einem einzigen Schritt codieren, während mit  $G = 4$  hierfür vier Schritte notwendig waren.

(5)  Richtig ist nur die Aussage 1.

• Ein Nachteil von LZ77 ist das lokale Wörterbuch.  Eigentlich schon bekannte Phrasen können nicht für die Datenkomprimierung verwendet werden, wenn sie mehr als  $G$  Zeichen vorher im Text aufgetreten sind.  Dagegen sind bei LZ78 alle Phrasen im globalen Wörterbuch abgelegt.
• Richtig ist zwar, dass bei LZ78 nur Pärchen  $(I, \ Z)$  übertragen werden müssen, während bei LZ77 jeder Codierschritt durch ein Triple  $(P, \ L, \ Z)$  gekennzeichnet ist.  Das bedeutet aber noch nicht, dass pro Codierschritt auch weniger Bit übertragen werden müssen.
• Betrachten wir beispielhaft die Puffergröße  $G = 8$.  Bei LZ77 muss man dann  $P$  mit drei Bit und  $L$  mit vier Bit dargestellen.  Beachten Sie bitte, dass die gefundene Übereinstimmung zwischen Vorschaupuffer und Suchpuffer auch im Vorschaupuffer enden darf.
• Das neue Zeichen  $Z$  benötigt bei LZ78 genau die gleiche Bitanzahl wie bei LZ77 (nämlich zwei Bit), wenn man wie hier vom Symbolumfang  $M = 4$  ausgeht.
• Die Aussage 2 wäre nur dann richtig, wenn  $N_{\rm I}$  kleiner wäre als  $N_{\rm P}+ N_{\rm L}$, beispielsweise  $N_{\rm I} = 6$. Das würde aber bedeuten, dass man die Wörterbuchgröße auf  $I = 2^6 = 64$  begrenzen müsste.  Dies reicht für große Dateien nicht aus.
• Unsere Überschlagsrechnung basiert allerdings auf einer einheitlichen Bitanzahl für den Index  $I$.  Mit variabler Bitanzahl für den Index kann man etliche Bit einsparen, indem man  $I$  nur mit so vielen Bit überträgt, wie es für den Codierschritt  $i$  erforderlich ist.
• Prinzipiell ändert das aber nichts an der Beschränkung der Wörterbuchgröße, was bei großen Dateien stets zu Problemen führen wird.