Aufgaben:Aufgabe 4.5: Transinformation aus 2D-WDF: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (9 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID2886__Inf_A_4_5_neu.png|right|frame|Vorgegebene Verbund- | + | [[Datei:P_ID2886__Inf_A_4_5_neu.png|right|frame|Vorgegebene Verbund-WDF]] |
| − | Vorgegeben sind hier die drei unterschiedlichen 2D–Gebiete $f_{XY}(x, y)$, die in der Aufgabe nach ihren Füllfarben mit | + | Vorgegeben sind hier die drei unterschiedlichen 2D–Gebiete $f_{XY}(x, y)$, die in der Aufgabe nach ihren Füllfarben mit |
| − | * | + | * rote Verbund-WDF, |
| − | * | + | * blaue Verbund-WDF, und |
| − | * | + | * grüne Verbund-WDF |
| − | |||
| − | Die Transinformation zwischen den wertkontinuierlichen Zufallsgrößen $X$ und $Y$ kann | + | bezeichnet werden. Innerhalb der dargestellten Gebieten gelte jeweils $f_{XY}(x, y) = C = \rm const.$ |
| + | |||
| + | Die Transinformation zwischen den wertkontinuierlichen Zufallsgrößen $X$ und $Y$ kann man zum Beispiel wie folgt berechnen: | ||
:$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ | :$$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$ | ||
Für die hier verwendeten differentiellen Entropien gelten die folgenden Gleichungen: | Für die hier verwendeten differentiellen Entropien gelten die folgenden Gleichungen: | ||
| − | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x | + | :$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y | + | :$$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
:$$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} | :$$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} | ||
| − | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} [ f_{XY}(x, y) ] | + | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] |
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$ | ||
| − | Für die beiden Randwahrscheinlichkeitsdichtefunktionen gilt dabei: | + | *Für die beiden Randwahrscheinlichkeitsdichtefunktionen gilt dabei: |
:$$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) | :$$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) | ||
\hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$ | \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$ | ||
| Zeile 29: | Zeile 30: | ||
| − | + | ||
| − | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN–Kanalkapazität bei wertkontinuierlichem Eingang]]. | + | |
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN–Kanalkapazität bei wertkontinuierlichem Eingang]]. | ||
| + | |||
*Gegeben seien zudem folgende differentielle Entropien: | *Gegeben seien zudem folgende differentielle Entropien: | ||
| − | * Ist $X$ dreieckverteilt zwischen $x_{\rm min}$ und $x_{\rm max}$, so gilt: | + | :* Ist $X$ dreieckverteilt zwischen $x_{\rm min}$ und $x_{\rm max}$, so gilt: |
| − | * Ist $Y$ gleichverteilt zwischen $y_{\rm min}$ und $y_{\rm max}$, so gilt: $h(Y) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}]\hspace{0.05cm}.$ | + | ::$$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$ |
| − | *Alle Ergebnisse sollen in „bit” angegeben werden. Dies erreicht man mit & | + | :* Ist $Y$ gleichverteilt zwischen $y_{\rm min}$ und $y_{\rm max}$, so gilt: |
| + | ::$$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$ | ||
| + | *Alle Ergebnisse sollen in „bit” angegeben werden. Dies erreicht man mit $\log$ ⇒ $\log_2$. | ||
| + | |||
| Zeile 43: | Zeile 51: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die Transinformation der roten Verbund-WDF? | + | {Wie groß ist die Transinformation <u>der roten Verbund-WDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0. } $\ \rm bit$ |
| − | {Wie groß ist die Transinformation der blauen Verbund-WDF? | + | {Wie groß ist die Transinformation <u>der blauen Verbund-WDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | {Wie groß ist die Transinformation der grünen Verbund-WDF? | + | {Wie groß ist die Transinformation <u>der grünen Verbund-WDF</u>? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $I(X; Y) \ = \ $ { 0.721 3% } $\ \rm bit$ |
| − | {Welche Voraussetzungen müssen die Zufallsgrößen $X$ und $Y$ gleichzeitig erfüllen, damit allgemein $I(X;Y) = 1/2 \cdot \log (\rm e)$ gilt: | + | {Welche Voraussetzungen müssen die Zufallsgrößen $X$ und $Y$ gleichzeitig erfüllen, damit allgemein $I(X;Y) = 1/2 \cdot \log (\rm e)$ gilt: |
|type="[]"} | |type="[]"} | ||
| − | + Die Verbund-WDF $f_{XY}(x, y)$ ergibt ein Parallelogramm. | + | + Die Verbund-WDF $f_{XY}(x, y)$ ergibt ein Parallelogramm. |
| − | + Eine der Zufallsgrößen ( | + | + Eine der Zufallsgrößen $(X$ oder $Y)$ ist gleichverteilt. |
| − | + Die andere Zufallsgröße ($ | + | + Die andere Zufallsgröße $(Y$ oder $X)$ ist dreieckverteilt. |
| Zeile 68: | Zeile 76: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[Datei:P_ID2887__Inf_A_4_5a.png|right|frame|„Rote” Wahrscheinlichkeitsdichtefunktionen]] | + | [[Datei:P_ID2887__Inf_A_4_5a.png|right|frame|„Rote” Wahrscheinlichkeitsdichtefunktionen; <br>'''!''' Ordinate von $f_{Y}(y)$ ist nach links gerichtet '''!''']] |
| − | '''(1)''' Bei der rechteckförmigen Verbund–WDF | + | '''(1)''' Bei der rechteckförmigen Verbund–WDF $f_{XY}(x, y)$ gibt es zwischen $X$ und $Y$ keine statistischen Bindungen ⇒ $\underline{I(X;Y) = 0}$. |
Formal lässt sich dieses Ergebnis mit der folgenden Gleichung nachweisen: | Formal lässt sich dieses Ergebnis mit der folgenden Gleichung nachweisen: | ||
:$$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$ | :$$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$ | ||
| − | Die rote Fläche 2D–WDF | + | *Die rote Fläche der 2D–WDF $f_{XY}(x, y)$ ist $F = 4$. Da $f_{XY}(x, y)$ in diesem Gebiet konstant ist und das Volumen unter $f_{XY}(x, y)$ gleich $1$ sein muss, gilt für die Höhe $C = 1/F = 1/4$. |
| + | *Daraus folgt für die differentielle Verbundentropie in „bit”: | ||
:$$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | :$$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} | ||
\hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] | \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] | ||
| Zeile 80: | Zeile 89: | ||
\hspace{-0.6cm} f_{XY}(x, y) | \hspace{-0.6cm} f_{XY}(x, y) | ||
\hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$ | \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$ | ||
| − | Es ist berücksichtigt, das das Doppelintegral gleich 1 ist. Die Pseudo–Einheit „bit” korrespondiert mit dem | + | *Es ist berücksichtigt, das das Doppelintegral gleich $1$ ist. Die Pseudo–Einheit „bit” korrespondiert mit dem "Logarithmus dualis" ⇒ „log<sub>2</sub>”. |
| − | * Die | + | |
| + | |||
| + | Weiterhin gilt: | ||
| + | * Die Randwahrscheinlichkeitsdichtefunktionen $f_{X}(x)$ und $f_{Y}(y)$ sind jeweils rechteckförmig ⇒ Gleichverteilung zwischen $0$ und $2$: | ||
:$$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$ | :$$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$ | ||
| + | [[Datei:P_ID2888__Inf_A_4_5b_neu.png|right|frame|„Blaue” Wahrscheinlichkeitsdichtefunktionen]] | ||
* Setzt man diese Ergebnisse in die obige Gleichung ein, so erhält man: | * Setzt man diese Ergebnisse in die obige Gleichung ein, so erhält man: | ||
:$$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} | :$$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} | ||
| Zeile 88: | Zeile 101: | ||
| − | |||
| − | |||
| − | Dagegen ist | + | '''(2)''' Auch bei diesem Parallelogramm ergibt sich $F = 4, \ C = 1/4$ sowie $h(XY) = 2$ bit. |
| − | :$$h(X) = {\rm log}_2 \hspace{0.1cm} [\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}] | + | *Die Zufallsgröße $Y$ ist hier wie in der Teilaufgabe '''(1)''' zwischen $0$ und $2$ gleichverteilt ⇒ $h(Y) = 1$ bit. |
| + | |||
| + | *Dagegen ist $X$ dreieckverteilt zwischen $0$ und $4$ $($mit Maximum bei $2)$. | ||
| + | *Es ergibt sich hierfür die gleiche differentielle Entropie $h(Y)$ wie bei einer symmetrischen Dreieckverteilung im Bereich zwischen $±2$ (siehe Angabenblatt): | ||
| + | :$$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] | ||
= 1.721 \,{\rm bit}$$ | = 1.721 \,{\rm bit}$$ | ||
:$$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} | :$$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | <br clear=all> | |
| − | |||
| − | |||
[[Datei:P_ID2889__Inf_A_4_5c_neu.png|right|frame|„Grüne” Wahrscheinlichkeitsdichtefunktionen]] | [[Datei:P_ID2889__Inf_A_4_5c_neu.png|right|frame|„Grüne” Wahrscheinlichkeitsdichtefunktionen]] | ||
'''(3)''' Bei den grünen Gegebenheiten ergeben sich folgende Eigenschaften: | '''(3)''' Bei den grünen Gegebenheiten ergeben sich folgende Eigenschaften: | ||
| Zeile 105: | Zeile 118: | ||
\Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) | \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Die Zufallsgröße | + | *Die Zufallsgröße $Y$ ist nun zwischen $0$ und $A$ gleichverteilt und die Zufallsgröße $X$ ist zwischen $0$ und $2B$ dreieckverteilt $($mit Maximum bei $B)$: |
:$$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) | :$$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) | ||
\hspace{0.05cm},$$ $$ | \hspace{0.05cm},$$ $$ | ||
h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$ | h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$ | ||
| − | Damit ergibt sich für die Transinformation zwischen | + | *Damit ergibt sich für die Transinformation zwischen $X$ und $Y$: |
:$$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$ | :$$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$ | ||
| − | :$$ = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} | + | :$$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
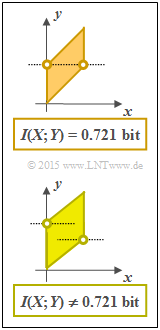
| − | + | [[Datei: P_ID2890__Inf_A_4_5d.png |right|frame|Weitere Beispiele für 2D–WDF $f_{XY}(x, y)$]] | |
| + | *$I(X;Y)$ somit unabhängig von den WDF–Parametern $A$ und $B$. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' <u>Alle genannten Voraussetzungen</u> sind erforderlich. Nicht für jedes Parallelogramm werden aber die Forderungen '''(2)''' und '''(3)''' erfüllt. | ||
| − | + | *Die nebenstehende Grafik zeigt zwei Konstellationen, wobei die Zufallsgröße $X$ jeweils gleichverteilt zwischen $0$ und $1$ ist. | |
| − | + | * Bei der oberen Grafik liegen die eingezeichneten Punkte auf einer Höhe ⇒ $f_{Y}(y)$ ist dreieckverteilt ⇒ $I(X;Y) = 0.721$ bit. | |
| − | * Bei der oberen Grafik liegen die | + | *Die untere Verbund–WDF besitzt eine andere Transinformation, da die beiden eingezeichneten Punkte nicht auf gleicher Höhe liegen <br>⇒ die WDF $f_{Y}(y)$ hat hier eine Trapezform. |
| − | *Die untere Verbund–WDF besitzt eine andere Transinformation, da die beiden Punkte nicht auf gleicher Höhe liegen ⇒ die WDF | + | *Gefühlsmäßig tippe ich auf $I(X;Y) < 0.721$ bit, da sich das 2D–Gebiet eher einem Rechteck annähert. Wenn Sie noch Lust haben, so überprüfen Sie diese Aussage. |
| − | *Gefühlsmäßig tippe ich auf | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 1. Oktober 2021, 17:13 Uhr
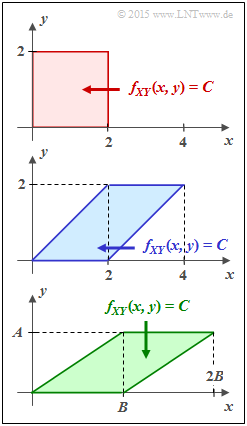
Vorgegeben sind hier die drei unterschiedlichen 2D–Gebiete $f_{XY}(x, y)$, die in der Aufgabe nach ihren Füllfarben mit
- rote Verbund-WDF,
- blaue Verbund-WDF, und
- grüne Verbund-WDF
bezeichnet werden. Innerhalb der dargestellten Gebieten gelte jeweils $f_{XY}(x, y) = C = \rm const.$
Die Transinformation zwischen den wertkontinuierlichen Zufallsgrößen $X$ und $Y$ kann man zum Beispiel wie folgt berechnen:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
Für die hier verwendeten differentiellen Entropien gelten die folgenden Gleichungen:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},$$
- $$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- Für die beiden Randwahrscheinlichkeitsdichtefunktionen gilt dabei:
- $$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$
- $$f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
- Gegeben seien zudem folgende differentielle Entropien:
- Ist $X$ dreieckverteilt zwischen $x_{\rm min}$ und $x_{\rm max}$, so gilt:
- $$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$
- Ist $Y$ gleichverteilt zwischen $y_{\rm min}$ und $y_{\rm max}$, so gilt:
- $$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$
- Alle Ergebnisse sollen in „bit” angegeben werden. Dies erreicht man mit $\log$ ⇒ $\log_2$.
Fragebogen
Musterlösung
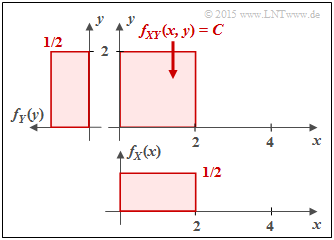
(1) Bei der rechteckförmigen Verbund–WDF $f_{XY}(x, y)$ gibt es zwischen $X$ und $Y$ keine statistischen Bindungen ⇒ $\underline{I(X;Y) = 0}$.
Formal lässt sich dieses Ergebnis mit der folgenden Gleichung nachweisen:
- $$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$
- Die rote Fläche der 2D–WDF $f_{XY}(x, y)$ ist $F = 4$. Da $f_{XY}(x, y)$ in diesem Gebiet konstant ist und das Volumen unter $f_{XY}(x, y)$ gleich $1$ sein muss, gilt für die Höhe $C = 1/F = 1/4$.
- Daraus folgt für die differentielle Verbundentropie in „bit”:
- $$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
- $$\Rightarrow \hspace{0.3cm} h(XY) \ = \ \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$
- Es ist berücksichtigt, das das Doppelintegral gleich $1$ ist. Die Pseudo–Einheit „bit” korrespondiert mit dem "Logarithmus dualis" ⇒ „log2”.
Weiterhin gilt:
- Die Randwahrscheinlichkeitsdichtefunktionen $f_{X}(x)$ und $f_{Y}(y)$ sind jeweils rechteckförmig ⇒ Gleichverteilung zwischen $0$ und $2$:
- $$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$
- Setzt man diese Ergebnisse in die obige Gleichung ein, so erhält man:
- $$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} \hspace{0.05cm}.$$
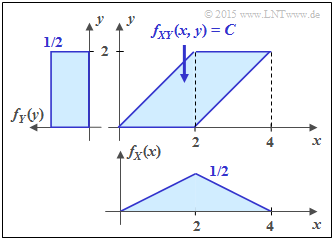
(2) Auch bei diesem Parallelogramm ergibt sich $F = 4, \ C = 1/4$ sowie $h(XY) = 2$ bit.
- Die Zufallsgröße $Y$ ist hier wie in der Teilaufgabe (1) zwischen $0$ und $2$ gleichverteilt ⇒ $h(Y) = 1$ bit.
- Dagegen ist $X$ dreieckverteilt zwischen $0$ und $4$ $($mit Maximum bei $2)$.
- Es ergibt sich hierfür die gleiche differentielle Entropie $h(Y)$ wie bei einer symmetrischen Dreieckverteilung im Bereich zwischen $±2$ (siehe Angabenblatt):
- $$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] = 1.721 \,{\rm bit}$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} \hspace{0.05cm}.$$
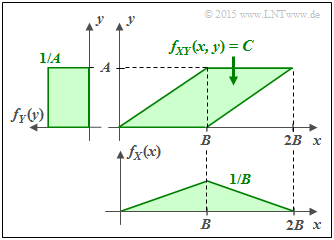
(3) Bei den grünen Gegebenheiten ergeben sich folgende Eigenschaften:
- $$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) \hspace{0.05cm}.$$
- Die Zufallsgröße $Y$ ist nun zwischen $0$ und $A$ gleichverteilt und die Zufallsgröße $X$ ist zwischen $0$ und $2B$ dreieckverteilt $($mit Maximum bei $B)$:
- $$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) \hspace{0.05cm},$$ $$ h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$
- Damit ergibt sich für die Transinformation zwischen $X$ und $Y$:
- $$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} \hspace{0.05cm}.$$
- $I(X;Y)$ somit unabhängig von den WDF–Parametern $A$ und $B$.
(4) Alle genannten Voraussetzungen sind erforderlich. Nicht für jedes Parallelogramm werden aber die Forderungen (2) und (3) erfüllt.
- Die nebenstehende Grafik zeigt zwei Konstellationen, wobei die Zufallsgröße $X$ jeweils gleichverteilt zwischen $0$ und $1$ ist.
- Bei der oberen Grafik liegen die eingezeichneten Punkte auf einer Höhe ⇒ $f_{Y}(y)$ ist dreieckverteilt ⇒ $I(X;Y) = 0.721$ bit.
- Die untere Verbund–WDF besitzt eine andere Transinformation, da die beiden eingezeichneten Punkte nicht auf gleicher Höhe liegen
⇒ die WDF $f_{Y}(y)$ hat hier eine Trapezform. - Gefühlsmäßig tippe ich auf $I(X;Y) < 0.721$ bit, da sich das 2D–Gebiet eher einem Rechteck annähert. Wenn Sie noch Lust haben, so überprüfen Sie diese Aussage.