Aufgaben:Aufgabe 5.1Z: cos² -Rauschbegrenzung: Unterschied zwischen den Versionen
K (Textersetzung - „\*\s*Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0\.” ein.“ durch „ “) |
|||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
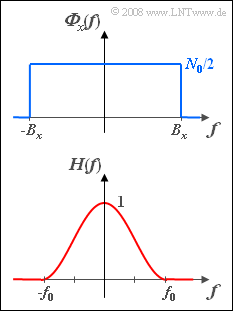
| − | [[Datei:P_ID491__Sto_Z_5_1.png|right| | + | [[Datei:P_ID491__Sto_Z_5_1.png|right|frame|oben: Eingangs–LDS ${\it Φ}_x(f)$, <br>unten: Filterfrequenzgang $H(f)$]] |
| − | Wir betrachten | + | Wir betrachten bandbegrenztes weißes Rauschen $x(t)$ mit dem oben skizzierten Leistungsdichtespektrum ${\it Φ}_x(f)$. Dieses ist im Bereich $|f| \le B_x$ konstant gleich $N_0/2$ und außerhalb gleich Null. |
Gehen Sie von folgenden Zahlenwerten aus: | Gehen Sie von folgenden Zahlenwerten aus: | ||
| − | *Rauschleistungsdichte $N_0 = 10^{-16} \ \rm V^2/Hz$, | + | *Rauschleistungsdichte $N_0 = 10^{-16} \ \rm V^2/Hz$, |
| − | *Rauschbandbreite $B_x = 10 \ \rm kHz$. | + | *(einseitige) Rauschbandbreite $B_x = 10 \ \rm kHz$. |
| + | |||
Dieses Signal wird an den Eingang eines Tiefpassfilters mit dem Frequenzgang | Dieses Signal wird an den Eingang eines Tiefpassfilters mit dem Frequenzgang | ||
| − | $$H(f) = \left\{ {\begin{array}{*{20}c} {\cos ^2 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)} & {\rm{f\ddot{u}r}\quad \left| \it f \right| \le \it f_{\rm 0} ,} \\ 0 & {{\rm{sonst}}} \\\end{array}} \right.$$ | + | :$$H(f) = \left\{ {\begin{array}{*{20}c} {\cos ^2 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)} & {\rm{f\ddot{u}r}\quad \left| \it f \right| \le \it f_{\rm 0} ,} \\ 0 & {{\rm{sonst}}} \\\end{array}} \right.$$ |
| + | |||
| + | angelegt. Hierbei bezeichnet $f_0$ die absolute Filterbandbreite, die zwischen $B_x/2$ und $2B_x$ variieren kann. Das Filterausgangssignal wird mit $y(t)$ bezeichnet. | ||
| + | |||
| − | |||
| − | |||
| − | + | Hinweise: | |
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Stochastische_Systemtheorie|Stochastische Systemtheorie]]. | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Stochastische_Systemtheorie|Stochastische Systemtheorie]]. |
| − | *Bezug genommen wird auch auf die Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|Gaußverteilte Zufallsgrößen]] sowie [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]]. | + | *Bezug genommen wird auch auf die Kapitel [[Stochastische_Signaltheorie/Gaußverteilte_Zufallsgrößen|Gaußverteilte Zufallsgrößen]] sowie [[Stochastische_Signaltheorie/Leistungsdichtespektrum_(LDS)|Leistungsdichtespektrum]]. |
| − | *Benutzen Sie, falls nötig, die nachfolgenden Gleichungen: | + | *Benutzen Sie, falls nötig, die nachfolgenden Gleichungen: |
| − | :$${\rm Q}(x) \approx \frac{1}{{\sqrt {2{\rm{\pi }}} \cdot x}} \cdot {\rm{e}}^{ - x^2 /2} \ | + | :$${\rm Q}(x) \approx \frac{1}{{\sqrt {2{\rm{\pi }}} \cdot x}} \cdot {\rm{e}}^{ - x^2 /2} \hspace{0.15cm}( |
| + | \text{für großes }x),$$ | ||
:$$\int {\rm{cos}}^{\rm{2}}( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{1}{2} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ),$$ | :$$\int {\rm{cos}}^{\rm{2}}( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{1}{2} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ),$$ | ||
:$$\int {\cos ^4 } ( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ) + \frac{1}{32a} \cdot \sin ( {4ax} ).$$ | :$$\int {\cos ^4 } ( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ) + \frac{1}{32a} \cdot \sin ( {4ax} ).$$ | ||
| + | |||
| + | |||
| Zeile 32: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist der Effektivwert des Eingangssignals $x(t)$? | + | {Wie groß ist der Effektivwert des Eingangssignals $x(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $\sigma_x \ = $ { 1 3% } $\ \rm | + | $\sigma_x \ = \ $ { 1 3% } $\ \rm µ V$ |
| − | {Wie groß ist die Wahrscheinlichkeit, dass ein momentaner Spannungswert des Eingangssignals betragsmäßig größer als $5 \hspace{0.05cm} \rm | + | {Wie groß ist die Wahrscheinlichkeit, dass ein momentaner Spannungswert des Eingangssignals betragsmäßig größer als $5 \hspace{0.05cm} \rm µ V$ ist? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(|x(t)| > 5 \hspace{0.05cm} \rm | + | ${\rm Pr}(|x(t)| > 5 \hspace{0.05cm} \rm µ V) \ = \ $ { 0.6 3% } $\ \cdot 10^{-6}$ |
| − | {Wie groß ist der Mittelwert (Gleichanteil) des Ausgangssignals $y(t)$? | + | {Wie groß ist der Mittelwert (Gleichanteil) des Ausgangssignals $y(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $m_y\ \ = $ { 0. } $\ \rm | + | $m_y\ \ = \ $ { 0. } $\ \rm µ V$ |
| − | {Berechnen Sie den Effektivwert des Ausgangssignals $y(t)$ für | + | {Berechnen Sie den Effektivwert des Ausgangssignals $y(t)$ für $f_0 = B_x/2$. |
| − | $f_0 = B_x/2$. | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_y \ = \ $ { 0.433 3% } $\ \rm µ V$ |
| − | {Berechnen Sie den Effektivwert von $y(t)$ unter der Bedingung $f_0 = 2 \cdot B_x$. | + | {Berechnen Sie den Effektivwert von $y(t)$ unter der Bedingung $f_0 = 2 \cdot B_x$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $\sigma_y \ = \ $ { 0.731 3% } $\ \rm µ V$ |
| − | {Es gelte weiter $f_0 = 2 \cdot B_x$. Wie groß ist die Wahrscheinlichkeit, dass das Ausgangssignal $y(t)$ betragsmäßig größer als $5 \hspace{0.05cm} \rm | + | {Es gelte weiter $f_0 = 2 \cdot B_x$. Wie groß ist die Wahrscheinlichkeit, dass das Ausgangssignal $y(t)$ betragsmäßig größer als $5 \hspace{0.05cm} \rm µ V$ ist? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(|y(t)| > 5 \hspace{0.05cm} \rm | + | ${\rm Pr}(|y(t)| > 5 \hspace{0.05cm} \rm µ V) \ = \ $ { 8 3% } $\ \cdot 10^{-12}$ |
| Zeile 68: | Zeile 72: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Varianz (Leistung) ⇒ Effektivwert zum Quadrat des Signals $x(t)$ beträgt | + | '''(1)''' Die Varianz (Leistung) ⇒ Effektivwert zum Quadrat des Signals $x(t)$ beträgt |
:$$\sigma _x ^2 = \frac{N_0 }{2} \cdot 2B_x = N_0 \cdot B_x = 10^{ - 12} \;{\rm{V}}^2 | :$$\sigma _x ^2 = \frac{N_0 }{2} \cdot 2B_x = N_0 \cdot B_x = 10^{ - 12} \;{\rm{V}}^2 | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm} | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} | ||
| − | \sigma _x \hspace{0.15cm}\underline{ = 1\,\,{\rm \ | + | \sigma _x \hspace{0.15cm}\underline{ = 1\,\,{\rm µ}{\rm V}}.$$ |
| + | |||
| + | |||
| + | '''(2)''' Entsprechend dem Kapitel „Gaußverteilte Zufallsgrößen” und der hier angegebenen Näherung $($für große $x)$ erhält man: | ||
| + | :$$\Pr \left( {\left| {x(t)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}(5) = \frac{2}{{\sqrt {2{\rm{\pi }}} \cdot 5}} \cdot {\rm{e}}^{ - 12.5}\hspace{0.15cm} \underline{ \approx 0.6 \cdot 10^{ - 6}} .$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Das Eingangssignal $x(t)$ ist mittelwertfrei ⇒ $m_x = 0$. | ||
| + | *Sonst müsste ${\it Φ}_x(f)$ noch eine Diracfunktion bei $f= 0$ beinhalten. | ||
| + | *Der Mittelwert wird durch das lineare Filter nicht verändert ⇒ $m_y\hspace{0.05cm}\underline{ = 0}$. | ||
| − | |||
| − | |||
| − | |||
'''(4)''' Für das Leistungsdichtespektrum des Ausgangssignals gilt allgemein: | '''(4)''' Für das Leistungsdichtespektrum des Ausgangssignals gilt allgemein: | ||
:$${\it \Phi}_y (f) = {N_0 }/{2} \cdot \left| {H( f )} \right|^2 .$$ | :$${\it \Phi}_y (f) = {N_0 }/{2} \cdot \left| {H( f )} \right|^2 .$$ | ||
| − | Damit kann die Varianz $\sigma _y^2$ berechnet werden. Unter Ausnützung der Symmetrie erhält man: | + | *Damit kann die Varianz $\sigma _y^2$ berechnet werden. Unter Ausnützung der Symmetrie erhält man: |
| − | :$$\sigma _y ^2 = {N_0 }/{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H( f )} \right|^2 | + | :$$\sigma _y ^2 = {N_0 }/{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = N_0 \cdot \int_0^{f_0 } {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f .$$ |
| + | |||
| + | *Das bestimmte Integral ist vorgegeben. Bei jedem der drei Lösungsterme ergibt sich für die untere Grenze der Wert Null. Daraus folgt: | ||
| + | :$$\sigma _y ^2 = {N_0}/{2} \cdot \left( {\frac{3}{8} \cdot f_0 + \frac{f_0 }{{2{\rm{\pi }}}} \cdot \sin ( {\rm{\pi }} ) + \frac{f_0 }{{16{\rm{\pi }}}} \cdot \sin ( {{\rm{2\pi }}} )} \right) = \frac{3}{8} \cdot N_0 \cdot f_0 $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} f_0 = B_x/2\text{:}\hspace{0.2cm}\sigma _y ^2 = \frac{3}{16} \cdot N_0 \cdot B_x = \frac{3}{16} \cdot \sigma _x ^2 = 0.1875 \cdot 10^{ - 12} \;{\rm{V}}^2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\sigma _y \hspace{0.15cm}\underline{ = 0.433\;{\rm{µ V}}}{\rm{.}}$$ | ||
| + | |||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' Nun besitzt das Eingangs- | + | '''(5)''' Nun besitzt das Eingangs-Leistungsdichtespektrum für $|f| > B_x$ keine Anteile. |
| + | *Deshalb gilt: | ||
:$$\sigma _y ^2 = N_0\cdot \int_0^{B_x } {\cos ^4 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f = N_0 \cdot \int_0^{f_0 /2} {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f.}$$ | :$$\sigma _y ^2 = N_0\cdot \int_0^{B_x } {\cos ^4 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f = N_0 \cdot \int_0^{f_0 /2} {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f.}$$ | ||
| − | Die numerische Auswertung liefert hierfür: | + | *Die numerische Auswertung liefert hierfür: |
| − | :$$\sigma _y ^2 = N_0 \left( {\frac{3}{8} \cdot B_x + \frac{B_x }{{2{\rm{\pi }}}} \cdot \sin ( {\frac{{\rm{\pi }}}{2}} ) + \frac{B_x }{{{\rm{16\pi }}}} \cdot \sin ( {\rm{\pi }} )} \right) = N_0 \cdot B_x \left( {\frac{3}{8} + \frac{1}{{2{\rm{\pi }}}}} \right) = 0.534\cdot \sigma _x ^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma _y \hspace{0.15cm}\underline{ = 0.731\;{\rm{ | + | :$$\sigma _y ^2 = N_0 \left( {\frac{3}{8} \cdot B_x + \frac{B_x }{{2{\rm{\pi }}}} \cdot \sin ( {\frac{{\rm{\pi }}}{2}} ) + \frac{B_x }{{{\rm{16\pi }}}} \cdot \sin ( {\rm{\pi }} )} \right) = N_0 \cdot B_x \left( {\frac{3}{8} + \frac{1}{{2{\rm{\pi }}}}} \right) = 0.534\cdot \sigma _x ^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma _y \hspace{0.15cm}\underline{ = 0.731\;{\rm{µ V}}}{\rm{.}}$$ |
| + | |||
| + | |||
| − | '''(6)''' Analog zur Musterlösung der Teilaufgabe (2) gilt: | + | '''(6)''' Analog zur Musterlösung der Teilaufgabe '''(2)''' gilt: |
| − | :$$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{ | + | :$$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}\left( {\frac{{5\;{\rm{µ V}}}}{{0.731\;{\rm{µ V}}}}} \right) = 2 \cdot {\rm Q}( {6.84} ).$$ |
| − | Mit der angegebenen Näherung hat diese Wahrscheinlichkeit den Wert $\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{ | + | *Mit der angegebenen Näherung hat diese Wahrscheinlichkeit den folgenden Wert: |
| + | :$$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) \hspace{0.15cm} \underline{ \approx 8 \cdot 10^{ - 12}}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 9. Februar 2022, 18:29 Uhr
Wir betrachten bandbegrenztes weißes Rauschen $x(t)$ mit dem oben skizzierten Leistungsdichtespektrum ${\it Φ}_x(f)$. Dieses ist im Bereich $|f| \le B_x$ konstant gleich $N_0/2$ und außerhalb gleich Null.
Gehen Sie von folgenden Zahlenwerten aus:
- Rauschleistungsdichte $N_0 = 10^{-16} \ \rm V^2/Hz$,
- (einseitige) Rauschbandbreite $B_x = 10 \ \rm kHz$.
Dieses Signal wird an den Eingang eines Tiefpassfilters mit dem Frequenzgang
- $$H(f) = \left\{ {\begin{array}{*{20}c} {\cos ^2 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)} & {\rm{f\ddot{u}r}\quad \left| \it f \right| \le \it f_{\rm 0} ,} \\ 0 & {{\rm{sonst}}} \\\end{array}} \right.$$
angelegt. Hierbei bezeichnet $f_0$ die absolute Filterbandbreite, die zwischen $B_x/2$ und $2B_x$ variieren kann. Das Filterausgangssignal wird mit $y(t)$ bezeichnet.
Hinweise:
- Die Aufgabe gehört zum Kapitel Stochastische Systemtheorie.
- Bezug genommen wird auch auf die Kapitel Gaußverteilte Zufallsgrößen sowie Leistungsdichtespektrum.
- Benutzen Sie, falls nötig, die nachfolgenden Gleichungen:
- $${\rm Q}(x) \approx \frac{1}{{\sqrt {2{\rm{\pi }}} \cdot x}} \cdot {\rm{e}}^{ - x^2 /2} \hspace{0.15cm}( \text{für großes }x),$$
- $$\int {\rm{cos}}^{\rm{2}}( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{1}{2} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ),$$
- $$\int {\cos ^4 } ( {ax} )\hspace{0.1cm}{\rm{d}}x = \frac{3}{8} \cdot x + \frac{1}{4a} \cdot \sin ( {2ax} ) + \frac{1}{32a} \cdot \sin ( {4ax} ).$$
Fragebogen
Musterlösung
- $$\sigma _x ^2 = \frac{N_0 }{2} \cdot 2B_x = N_0 \cdot B_x = 10^{ - 12} \;{\rm{V}}^2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma _x \hspace{0.15cm}\underline{ = 1\,\,{\rm µ}{\rm V}}.$$
(2) Entsprechend dem Kapitel „Gaußverteilte Zufallsgrößen” und der hier angegebenen Näherung $($für große $x)$ erhält man:
- $$\Pr \left( {\left| {x(t)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}(5) = \frac{2}{{\sqrt {2{\rm{\pi }}} \cdot 5}} \cdot {\rm{e}}^{ - 12.5}\hspace{0.15cm} \underline{ \approx 0.6 \cdot 10^{ - 6}} .$$
(3) Das Eingangssignal $x(t)$ ist mittelwertfrei ⇒ $m_x = 0$.
- Sonst müsste ${\it Φ}_x(f)$ noch eine Diracfunktion bei $f= 0$ beinhalten.
- Der Mittelwert wird durch das lineare Filter nicht verändert ⇒ $m_y\hspace{0.05cm}\underline{ = 0}$.
(4) Für das Leistungsdichtespektrum des Ausgangssignals gilt allgemein:
- $${\it \Phi}_y (f) = {N_0 }/{2} \cdot \left| {H( f )} \right|^2 .$$
- Damit kann die Varianz $\sigma _y^2$ berechnet werden. Unter Ausnützung der Symmetrie erhält man:
- $$\sigma _y ^2 = {N_0 }/{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H( f )} \right|^2 \hspace{0.1cm}{\rm{d}}f} = N_0 \cdot \int_0^{f_0 } {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f .$$
- Das bestimmte Integral ist vorgegeben. Bei jedem der drei Lösungsterme ergibt sich für die untere Grenze der Wert Null. Daraus folgt:
- $$\sigma _y ^2 = {N_0}/{2} \cdot \left( {\frac{3}{8} \cdot f_0 + \frac{f_0 }{{2{\rm{\pi }}}} \cdot \sin ( {\rm{\pi }} ) + \frac{f_0 }{{16{\rm{\pi }}}} \cdot \sin ( {{\rm{2\pi }}} )} \right) = \frac{3}{8} \cdot N_0 \cdot f_0 $$
- $$\Rightarrow \hspace{0.3cm} f_0 = B_x/2\text{:}\hspace{0.2cm}\sigma _y ^2 = \frac{3}{16} \cdot N_0 \cdot B_x = \frac{3}{16} \cdot \sigma _x ^2 = 0.1875 \cdot 10^{ - 12} \;{\rm{V}}^2 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\sigma _y \hspace{0.15cm}\underline{ = 0.433\;{\rm{µ V}}}{\rm{.}}$$
(5) Nun besitzt das Eingangs-Leistungsdichtespektrum für $|f| > B_x$ keine Anteile.
- Deshalb gilt:
- $$\sigma _y ^2 = N_0\cdot \int_0^{B_x } {\cos ^4 \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f = N_0 \cdot \int_0^{f_0 /2} {\cos ^4 } \left( {\frac{{{\rm{\pi }}f}}{2f_0 }} \right)\hspace{0.1cm}{\rm{d}}f.}$$
- Die numerische Auswertung liefert hierfür:
- $$\sigma _y ^2 = N_0 \left( {\frac{3}{8} \cdot B_x + \frac{B_x }{{2{\rm{\pi }}}} \cdot \sin ( {\frac{{\rm{\pi }}}{2}} ) + \frac{B_x }{{{\rm{16\pi }}}} \cdot \sin ( {\rm{\pi }} )} \right) = N_0 \cdot B_x \left( {\frac{3}{8} + \frac{1}{{2{\rm{\pi }}}}} \right) = 0.534\cdot \sigma _x ^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma _y \hspace{0.15cm}\underline{ = 0.731\;{\rm{µ V}}}{\rm{.}}$$
(6) Analog zur Musterlösung der Teilaufgabe (2) gilt:
- $$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) = 2 \cdot {\rm Q}\left( {\frac{{5\;{\rm{µ V}}}}{{0.731\;{\rm{µ V}}}}} \right) = 2 \cdot {\rm Q}( {6.84} ).$$
- Mit der angegebenen Näherung hat diese Wahrscheinlichkeit den folgenden Wert:
- $$\Pr \left( {\left| {y\left( t \right)} \right| > 5\;{\rm{µ V}}} \right) \hspace{0.15cm} \underline{ \approx 8 \cdot 10^{ - 12}}.$$