| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
<br> | <br> | ||
| − | Im Abschnitt [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Beispiele_und_Eigenschaften_von_Galoisfeldern|Beispiel 2]] im Kapitel „Einige Grundlagen der Algebra” wurde bereits gezeigt, dass die '''endliche Zahlenmenge''' $\{0, 1, 2, 3\}$ ⇒ $q = 4$ nicht die Eigenschaften eines Galoisfeldes $\rm GF(4)$ erfüllt. Vielmehr ergeben sich für die ''Addition'' modulo 4 und die ''Multiplikation'' modulo 4 folgende Tabellen: | + | Im Abschnitt [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Beispiele_und_Eigenschaften_von_Galoisfeldern|$\text{Beispiel 2}$]] im Kapitel „Einige Grundlagen der Algebra” wurde bereits gezeigt, dass die '''endliche Zahlenmenge''' $\{0, 1, 2, 3\}$ ⇒ $q = 4$ nicht die Eigenschaften eines Galoisfeldes $\rm GF(4)$ erfüllt. Vielmehr ergeben sich für die ''Addition'' modulo 4 und die ''Multiplikation'' modulo 4 folgende Tabellen: |
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Zeile 29: | Zeile 29: | ||
| − | Für $z_i = 2$ gibt es keine multiplikative Inverse ${\rm Inv_M}(z_i)$. Dies erkennt man daran, dass kein einziges Element $z_i ∈ \{0, 1, 2, 3\}$ die Bedingung $2 · z_i = 1$ erfüllt. | + | Für $z_i = 2$ gibt es keine multiplikative Inverse ${\rm Inv_M}(z_i)$. Dies erkennt man daran, dass kein einziges Element $z_i ∈ \{0, 1, 2, 3\}$ die Bedingung $2 · z_i = 1$ erfüllt. |
| − | Geht man dagegen vom binären Galoisfeld ${\rm GF}(2) = \{0, 1\}$ aus und erweitert dieses entsprechend der Gleichung | + | Geht man dagegen vom binären Galoisfeld ${\rm GF}(2) = \{0, 1\}$ aus und erweitert dieses entsprechend der Gleichung |
::<math>{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ \big | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, </math> | ::<math>{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ \big | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, </math> | ||
| − | so ergibt sich die ebenfalls '''endliche <b>Menge''' $\{0, 1, \alpha, 1 + \alpha\}$</b> ⇒ die Ordnung ist weiterhin $q=4$. Führt man die Rechenoperationen modulo $p(\alpha) = \alpha^2 + \alpha + 1$ durch, so erhält man das folgende Ergebnis: | + | so ergibt sich die ebenfalls '''endliche <b>Menge''' $\{0, 1, \alpha, 1 + \alpha\}$</b> ⇒ die Ordnung ist weiterhin $q=4$. |
| + | |||
| + | Führt man die Rechenoperationen modulo $p(\alpha) = \alpha^2 + \alpha + 1$ durch, so erhält man das folgende Ergebnis: | ||
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Zeile 55: | Zeile 57: | ||
Hierzu ist anzumerken: | Hierzu ist anzumerken: | ||
| − | *Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin $N_{\rm A} = 0$ und $N_{\rm M} = 1$ . | + | *Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin $N_{\rm A} = 0$ und $N_{\rm M} = 1$. |
| − | *Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist $\alpha + \alpha = \alpha - \alpha = 0$. | + | *Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist $\alpha + \alpha = \alpha - \alpha = 0$. |
| − | *Für alle | + | *Für alle $z_i$ gilt somit: Die additive Inverse von $z_i$ ist das Element $z_i$ selbst. |
*Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen: | *Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen: | ||
| Zeile 71: | Zeile 73: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Zwischenergebnis:}$ | $\text{Zwischenergebnis:}$ | ||
| − | *Die Menge $\{0, 1, \alpha, 1 + \alpha\}$ stellt zusammen mit den | + | *Die Menge $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ stellt zusammen mit den beiden Operationen <i>Addition</i> und <i>Multiplikation</i> modulo $p(\alpha)= \alpha^2 + \alpha + 1$ ein <i>Galoisfeld</i> dar. Die Ordnung ist $q = 4$. |
| − | *Dieses mit $\rm GF(2^2) = GF(4)$ bezeichnete Galoisfeld erfüllt alle im [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Definition_eines_Galoisfeldes| vorherigen Kapitel ]] genannten Anforderungen.<br> | + | *Dieses mit $\rm GF(2^2) = GF(4)$ bezeichnete Galoisfeld erfüllt alle im [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Definition_eines_Galoisfeldes| vorherigen Kapitel ]] genannten Anforderungen.<br> |
| − | *Im Gegensatz zum Zahlenkörper $\rm GF(3) = \{0, 1, 2\}$ mit der Eigenschaft, dass $q = 3$ eine Primzahl ist, nennt man $\rm GF(2^2)$ einen <b>Erweiterungskörper </b>(englisch: <i>Extension Field</i> ).}}<br> | + | *Im Gegensatz zum Zahlenkörper $\rm GF(3) = \{0, \ 1, \ 2\}$ mit der Eigenschaft, dass $q = 3$ eine Primzahl ist, nennt man $\rm GF(2^2)$ einen <b>Erweiterungskörper </b> (englisch: <i>Extension Field</i> ).}}<br> |
== Reduzible und irreduzible Polynome == | == Reduzible und irreduzible Polynome == | ||
<br> | <br> | ||
| − | Das Polynom $p(\alpha)$ und damit die Bestimmungsgleichung $p(\alpha) = 0$ darf nicht beliebig vorgegeben werden. Das auf der letzten Seite verwendete Polynom $p(\alpha)= \alpha^2 + \alpha + 1$ | + | Das Polynom $p(\alpha)$ und damit die Bestimmungsgleichung $p(\alpha) = 0$ darf nicht beliebig vorgegeben werden. Das auf der letzten Seite verwendete Polynom |
| + | :$$p(\alpha)= \alpha^2 + \alpha + 1$$ | ||
| + | ist geeignet. Nun versuchen wir es mit einem anderen Polynom, nämlich $p(\alpha)= \alpha^2 + 1$. | ||
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Zeile 97: | Zeile 101: | ||
Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten: | Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten: | ||
| − | *Aus $p(\alpha) = 0$ folgt nun für das Produkt $\alpha \cdot \alpha = 1$ und das Produkt $(1 +\alpha) \cdot (1 +\alpha) $ ergibt das Nullelement. Das gemischte Produkt | + | *Aus $p(\alpha) = 0$ folgt nun für das Produkt $\alpha \cdot \alpha = 1$ und das Produkt $(1 +\alpha) \cdot (1 +\alpha) $ ergibt das Nullelement. Das gemischte Produkt ist $\alpha \cdot (1 +\alpha) = 1 +\alpha $.<br> |
| − | *In der letzten Zeile der | + | *In der letzten Zeile der Multiplikationstabelle und auch in der letzten Spalte steht nun keine „$1$” ⇒ Hinsichtlich der Bedingung $p(\alpha)= \alpha^2 + 1= 0$ existiert demzufolge die multiplikative Inverse zu $1 +\alpha$ nicht.<br> |
| − | *Damit erfüllt aber die endliche Menge $\{0, 1, \alpha, 1 + \alpha\}$ zusammen mit Rechenoperationen modulo $p(\alpha)= \alpha^2 + 1$ auch nicht die Voraussetzungen eines Erweiterungskörpers $\rm GF(2^2) $.<br><br> | + | *Damit erfüllt aber die endliche Menge $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ zusammen mit Rechenoperationen modulo $p(\alpha)= \alpha^2 + 1$ auch nicht die Voraussetzungen eines Erweiterungskörpers $\rm GF(2^2) $.<br><br> |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Fassen wir zusammen:}$ Aus dem binären Galoisfeld $\rm GF(2) = \{0, 1\}$ lässt sich unter Zuhilfenahme eines Polynoms vom Grad $m = 2$ mit binären Koeffizienten, | + | $\text{Fassen wir zusammen:}$ |
| + | |||
| + | Aus dem binären Galoisfeld $\rm GF(2) = \{0, \ 1\}$ lässt sich unter Zuhilfenahme eines Polynoms vom Grad $m = 2$ mit binären Koeffizienten, | ||
::<math>p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} | ::<math>p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | ein Erweiterungskörper $\rm GF(2^2)$ formulieren. <i>Anmerkung:</i> Die Umbenennung der | + | ein Erweiterungskörper $\rm GF(2^2)$ formulieren. <i>Anmerkung:</i> Die Umbenennung der Variablen $\alpha$ in $x$ hat nur formale Bedeutung im Hinblick auf spätere Seiten.<br> |
| − | *Im vorliegenden Fall gibt es nur ein geeignetes Polynom $p_1(x)= x^2 + x + 1$. Alle anderen möglichen Polynome vom Grad $m = 2$, nämlich | + | *Im vorliegenden Fall gibt es nur ein geeignetes Polynom $p_1(x)= x^2 + x + 1$. Alle anderen möglichen Polynome vom Grad $m = 2$, nämlich |
::<math>p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},</math> | ::<math>p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},</math> | ||
::<math>p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},</math> | ::<math>p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},</math> | ||
::<math>p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, </math> | ::<math>p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, </math> | ||
| − | + | :lassen sich faktorisieren und ergeben keinen Erweiterungskörper. | |
| − | lassen sich faktorisieren und ergeben keinen Erweiterungskörper. | + | *Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ ''reduzibel''. |
| − | *Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ ''reduzibel''. Der Schluss liegt nahe, dass für einen Erweiterungskörper nur ''irreduzible Polynome'' wie $p_1(x)$ geeignet sind.}}<br> | + | *Der Schluss liegt nahe, dass für einen Erweiterungskörper nur ''irreduzible Polynome'' wie $p_1(x)$ geeignet sind.}}<br> |
| Zeile 123: | Zeile 129: | ||
== Interpretation des neuen Elementes „alpha” == | == Interpretation des neuen Elementes „alpha” == | ||
<br> | <br> | ||
| − | Wir betrachten weiterhin den Körper ${\rm GF}(2^2) = \{0, 1, \alpha, 1 + \alpha\}$ entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreduzibles Ploynom): | + | Wir betrachten weiterhin den Körper ${\rm GF}(2^2) = \{0, \ 1,\ \alpha,\ 1 + \alpha\}$ entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreduzibles Ploynom): |
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Zeile 143: | Zeile 149: | ||
| − | [[Datei:P ID2552 KC T 2 2 S1 v2.png|right|frame|Übergang von ${\rm GF}(2)$ auf ${\rm GF}(2^2)$ |class=fit]] | + | [[Datei:P ID2552 KC T 2 2 S1 v2.png|right|frame|Übergang von ${\rm GF}(2)$ auf ${\rm GF}(2^2)$ |class=fit]] |
Welche Bedeutung hat aber nun das neue Element $\alpha$? | Welche Bedeutung hat aber nun das neue Element $\alpha$? | ||
| − | *Das Polynom $p(\alpha)= \alpha^2 + \alpha + 1 $ hat in ${\rm GF}(2) = \{0, 1\}$ keine Nullstelle. Das bedeutet weiter, dass $\alpha$ weder $0$ noch $1$ sein kann.<br> | + | *Das Polynom $p(\alpha)= \alpha^2 + \alpha + 1 $ hat in ${\rm GF}(2) = \{0, \ 1\}$ keine Nullstelle. Das bedeutet weiter, dass $\alpha$ weder $0$ noch $1$ sein kann.<br> |
| − | *Wäre $\alpha= 0$ bzw. $\alpha= 1$, so wären zudem zwei der vier Mengenelemente $\{0, 1, \alpha, 1 + \alpha\}$ jeweils identisch: Entweder „$0$” und „$\alpha$” sowie „$1$” und „$1+\alpha$” oder „$1$” und „$\alpha$” sowie „$0$” und „$1+\alpha$”. | + | *Wäre $\alpha= 0$ bzw. $\alpha= 1$, so wären zudem zwei der vier Mengenelemente $\{0,\ 1,\ \alpha,\ 1 + \alpha\}$ jeweils identisch: Entweder „$0$” und „$\alpha$” sowie „$1$” und „$1+\alpha$” oder „$1$” und „$\alpha$” sowie „$0$” und „$1+\alpha$”. |
| − | *Vielmehr erhält der eindimensionale Körper ${\rm GF}(2)$ durch die Einführung des Elementes $\alpha$ eine zweite Dimension. Er wird also zum Galoisfeld ${\rm GF}(2^2)$ erweitert, wie die nebenstehende Grafik zeigt. | + | *Vielmehr erhält der eindimensionale Körper ${\rm GF}(2)$ durch die Einführung des Elementes $\alpha$ eine zweite Dimension. Er wird also zum Galoisfeld ${\rm GF}(2^2)$ erweitert, wie die nebenstehende Grafik zeigt. |
| − | *Das Element $\alpha$ hat ähnliche Bedeutung wie die imaginäre Einheit ${\rm j}$, durch die man die Menge der reellen Zahlen unter der Nebenbedingung ${\rm j}^2 + 1 = 0$ zur Menge der komplexen Zahlen erweitert. | + | *Das Element $\alpha$ hat ähnliche Bedeutung wie die imaginäre Einheit ${\rm j}$, durch die man die Menge der reellen Zahlen unter der Nebenbedingung ${\rm j}^2 + 1 = 0$ zur Menge der komplexen Zahlen erweitert. |
<br clear=all> | <br clear=all> | ||
| Zeile 157: | Zeile 163: | ||
$\text{Übliche Darstellung des binären Erweiterungskörpers}\ {\rm GF}(2^2)\text{:}$ | $\text{Übliche Darstellung des binären Erweiterungskörpers}\ {\rm GF}(2^2)\text{:}$ | ||
| − | Aufgrund der Identität $\alpha^2 = 1 + \alpha$, die aus der Nebenbedingung $p(\alpha) = 0$ folgt, kann man in gleicher Weise ${\rm GF}(2^2) = \{0, 1, \alpha, \alpha^2\}$ schreiben, wobei nun folgende Operationstabellen gelten: | + | Aufgrund der Identität $\alpha^2 = 1 + \alpha$, die aus der Nebenbedingung $p(\alpha) = 0$ folgt, kann man in gleicher Weise ${\rm GF}(2^2) = \{0,\ 1,\ \alpha,\ \alpha^2\}$ schreiben, wobei nun folgende Operationstabellen gelten: |
:$$ \begin{array}{c} | :$$ \begin{array}{c} | ||
| Zeile 181: | Zeile 187: | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Ein '''Polynom''' in einem endlichen Körper ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt, hat folgende Form: | + | $\text{Definition:}$ Ein '''Polynom''' in einem endlichen Körper ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt, hat folgende Form: |
::<math>a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} | ::<math>a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
Anzumerken ist: | Anzumerken ist: | ||
| − | *Alle Koeffizienten $a_i $ sind Elemente des Körpers: $a_i \in {\rm GF}(P)$.<br> | + | *Alle Koeffizienten $a_i $ sind Elemente des Körpers: $a_i \in {\rm GF}(P)$.<br> |
| − | *Ist der führende Koeffizient $a_m ≠ 0$, so gibt $m$ den '''Grad''' des Polynoms an.}}<br> | + | *Ist der führende Koeffizient $a_m ≠ 0$, so gibt $m$ den '''Grad''' des Polynoms an.}}<br> |
| − | Betrachten wir ein dazu zweites Polynom mit Grad $M$, | + | Betrachten wir ein dazu zweites Polynom mit Grad $M$, |
::<math>b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} | ::<math>b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} | ||
\hspace{0.05cm},</math> | \hspace{0.05cm},</math> | ||
| − | so erhält man für die Summe (bzw. Differenz) und das Produkt jeweils in ${\rm GF}(P)$: | + | so erhält man für die Summe (bzw. Differenz) und das Produkt jeweils in ${\rm GF}(P)$: |
::<math>a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},</math> | ::<math>a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},</math> | ||
| Zeile 203: | Zeile 209: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Es gelte $a(x) = x^3 + x + 1$ und $b(x) = x^2 + x + 1$. | + | $\text{Beispiel 1:}$ Es gelte $a(x) = x^3 + x + 1$ und $b(x) = x^2 + x + 1$. |
| − | + | Im binären Galoisfeld ⇒ ${\rm GF}(2)$ ergibt sich nach den obigen Gleichungen für die Summe, die Differenz und das Produkt der beiden Polynome: | |
| − | |||
| + | ::<math>s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, </math> | ||
| + | ::<math>d(x) = a(x) - b(x) = x^3 + x^2 = s(x)\hspace{0.05cm},</math> | ||
::<math>c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} | ::<math>c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} | ||
c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} | c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} | ||
\hspace{0.05cm}.</math> | \hspace{0.05cm}.</math> | ||
| − | Mit $a_0 = a_1 = a_3 = b_0 = b_1 =b_2 = 1$ und $a_2 = a_4 = a_5 = b_3 = b_4 =b_5 = 0$ erhält man: | + | Mit $a_0 = a_1 = a_3 = b_0 = b_1 =b_2 = 1$ und $a_2 = a_4 = a_5 = b_3 = b_4 =b_5 = 0$ erhält man: |
::<math>c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},</math> | ::<math>c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},</math> | ||
| Zeile 226: | Zeile 233: | ||
::<math>\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.</math> | ::<math>\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.</math> | ||
| − | Im Galoisfeld ${\rm GF}(3)$ erhält man aufgrund der Modulo–3–Operationen andere Ergebnisse: | + | Im Galoisfeld ${\rm GF}(3)$ erhält man aufgrund der Modulo–3–Operationen andere Ergebnisse: |
::<math>s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},</math> | ::<math>s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},</math> | ||
| Zeile 233: | Zeile 240: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Ein Polynom $a(x)$ bezeichnet man als '''reduzibel''' (englisch: <i>reducible</i>), wenn es als Produkt zweier Polynome $p(x)$ und $q(x)$ mit jeweils niedrigerem Grad dargestellt werden kann: | + | $\text{Definition:}$ Ein Polynom $a(x)$ bezeichnet man als '''reduzibel''' (englisch: <i>reducible</i>), wenn es als Produkt zweier Polynome $p(x)$ und $q(x)$ mit jeweils niedrigerem Grad dargestellt werden kann: |
::<math>a(x) = p(x) \cdot q(x) | ::<math>a(x) = p(x) \cdot q(x) | ||
| Zeile 242: | Zeile 249: | ||
::<math>a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0</math> | ::<math>a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0</math> | ||
| − | gilt, so spricht man von einem '''irreduziblen''' (englisch: <i>irreducible</i> oder <i>prime</i>) Polynom.}}<br> | + | gilt, so spricht man von einem '''irreduziblen''' (englisch: <i>irreducible</i> oder <i>prime</i>) Polynom.}}<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$. Die Grafik verdeutlicht links die Modulo–2–Multiplikation $a(x)= b(x) \cdot p_1(x)$. Das Ergebnis ist $a(x) = x^5 + x^4 + 1$.<br> | + | $\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$. |
| + | |||
| + | Die Grafik verdeutlicht links die Modulo–2–Multiplikation $a(x)= b(x) \cdot p_1(x)$. Das Ergebnis ist $a(x) = x^5 + x^4 + 1$.<br> | ||
[[Datei:P ID2538 KC T 2 2 S2 v2.png|center|frame|Beispiel für Polynom–Multiplikation und –Division|class=fit]] | [[Datei:P ID2538 KC T 2 2 S2 v2.png|center|frame|Beispiel für Polynom–Multiplikation und –Division|class=fit]] | ||
| Zeile 255: | Zeile 264: | ||
::<math>p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}</math> | ::<math>p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}</math> | ||
| − | einen Rest $r(x) ≠ 0$ liefert. Dies würde im vorliegenden Beispiel (nahezu) $2^5 = 32$ Divisionen erfordern.<br> | + | einen Rest $r(x) ≠ 0$ liefert. Dies würde im vorliegenden Beispiel (nahezu) $2^5 = 32$ Divisionen erfordern.<br> |
Aufgrund unserer linken Berechnung können wir hier sofort erkennen, dass $a(x)$ mit Sicherheit kein irreduzibles Polynom ist, da zum Beispiel $a(x) = x^5 + x^4 + 1$ dividiert durch $p_1(x) = x^2 + x + 1$ das Polynom $b(x) = x^3 + x + 1$ ohne Rest ergibt.}}<br> | Aufgrund unserer linken Berechnung können wir hier sofort erkennen, dass $a(x)$ mit Sicherheit kein irreduzibles Polynom ist, da zum Beispiel $a(x) = x^5 + x^4 + 1$ dividiert durch $p_1(x) = x^2 + x + 1$ das Polynom $b(x) = x^3 + x + 1$ ohne Rest ergibt.}}<br> | ||
| Zeile 262: | Zeile 271: | ||
<br> | <br> | ||
Wir gehen von folgenden Voraussetzungen aus: | Wir gehen von folgenden Voraussetzungen aus: | ||
| − | *einem Galoisfeld ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt,<br> | + | *einem Galoisfeld ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt,<br> |
| − | *einem irreduziblen Polynom $p(x)$ über ${\rm GF}(P)$ | + | *einem irreduziblen Polynom $p(x)$ über ${\rm GF}(P)$ vom Grad $m$: |
::<math>p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} | ::<math>p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} | ||
| Zeile 272: | Zeile 281: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Es sei $P$ eine Primzahl, $m$ ganzzahlig, $p(x)$ ein irreduzibles Polynom vom Grad $m$ und es gelte $p(\alpha) = 0$. | + | $\text{Definition:}$ Es sei $P$ eine Primzahl, $m$ ganzzahlig, $p(x)$ ein irreduzibles Polynom vom Grad $m$ und es gelte $p(\alpha) = 0$. |
| − | Ein <b>Erweiterungskörper</b> lässt sich dann wie folgt beschreiben. | + | Ein <b>Erweiterungskörper</b> lässt sich dann wie folgt beschreiben. |
| − | ::<math>{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}\text{...} \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{\vert}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, P-1\}\Big \}</math> | + | ::<math>{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}\text{...} \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{\vert}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, P-1\}\Big \}.</math> |
| − | *Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der | + | *Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der Polynom–Addition und Polynom–Multiplikation modulo $p(\alpha)$.<br> |
| − | *Ein Galoisfeld ${\rm GF}(q)$ mit $q$ Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form $q = P^m$ geschrieben werden kann ( | + | *Ein Galoisfeld ${\rm GF}(q)$ mit $q$ Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form $q = P^m$ geschrieben werden kann <br>$(P$ kennzeichnet eine Primzahl, $m$ sei ganzzahlig$)$.}}<br> |
| − | [[Datei:P ID2500 KC T 2 2 S3 v2.png| | + | [[Datei:P ID2500 KC T 2 2 S3 v2.png|right|frame|Mögliche Galoisfelder ${\rm GF}(q)$ für $q ≤ 64$ |class=fit]] |
| − | Die Grafik zeigt, für welche $q$–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten Werte ist kein endlicher Körper angebbar. | + | Die Grafik zeigt, für welche $q$–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten Werte ist kein endlicher Körper angebbar. |
| − | |||
| − | *Die | + | Weiter ist anzumerken: |
| + | *Die gelb hinterlegten Positionen $q=P$ ⇒ $m = 1$ markieren Zahlenmengen $\{0,\ 1,\hspace{0.05cm}\text{ ...} \hspace{0.05cm},\ q- 1\}$ mit Galoiseigenschaften, siehe Seite [[Kanalcodierung/Einige_Grundlagen_der_Algebra#Definition_eines_Galoisfeldes| Definition eines Galoisfeldes]].<br> | ||
| + | |||
| + | *Die anderen Hinterlegungsfarben markieren Erweiterungskörper mit $q=P^m$, $m ≥ 2$. Für $q ≤ 64$ basieren diese auf den Primzahlen $2$, $3$, $5$ und $7$.<br> | ||
*Mit roter Schrift hervorgehoben sind binäre Körper ⇒ $q=2^m$, $m ≥ 1$, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.<br> | *Mit roter Schrift hervorgehoben sind binäre Körper ⇒ $q=2^m$, $m ≥ 1$, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.<br> | ||
| − | + | <br clear=all> | |
| − | |||
| − | |||
| − | |||
== Binäre Erweiterungskörper – Primitive Polynome== | == Binäre Erweiterungskörper – Primitive Polynome== | ||
<br> | <br> | ||
| + | [[Datei:P ID2501 KC T 2 2 S4 v4.png|right|frame|Irreduzible und primitive Polynome|class=fit]] | ||
Im Folgenden betrachten wir binäre Erweiterungskörper mit | Im Folgenden betrachten wir binäre Erweiterungskörper mit | ||
| − | ::<math>q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4, 8, 16, 32, 64, \text{...}</math | + | ::<math>q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4,\ 8,\ 16, 32,\ 64,\ \text{...}</math> |
| − | |||
| − | |||
| − | + | Elementen. | |
| + | *In der Tabelle sind für $2 ≤ m ≤ 6$ alle irreduziblen Polynome des Galoisfeldes ${\rm GF}(2)$ angegeben. | ||
| + | *Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern zusätzlich auch primitiv.<br> | ||
| + | *Primitive Polynome liefern auch die Grundlage für die [[Stochastische_Signaltheorie/Erzeugung_von_diskreten_Zufallsgr%C3%B6%C3%9Fen#Realisierung_von_PN-Generatoren| Realisierung von Pseudo–Noise–Generatoren]].<br> | ||
| − | |||
| − | Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten | + | Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten „primitiver Elemente” am Beispiel von |
::<math>{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.05cm}z_{q-1}\}</math> | ::<math>{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.05cm}z_{q-1}\}</math> | ||
| − | genannt werden. Das Element $z_i = \beta$ wird dann als '''primitiv''' bezeichnet, | + | genannt werden. Das Element $z_i = \beta$ wird dann als '''primitiv''' bezeichnet, |
| − | *wenn die Potenz $\beta^{\hspace{0.05cm}i}$ modulo $q$ zum ersten Mal für $i = q-1$ zum Ergebnis „$1$” führt, so dass <br> | + | *wenn die Potenz $\beta^{\hspace{0.05cm}i}$ modulo $q$ zum ersten Mal für $i = q-1$ zum Ergebnis „$1$” führt, so dass <br> |
| − | *$\beta^{\hspace{0.05cm}i}$ für $1 ≤ i ≤ q- 1$ genau die Elemente $z_1$, ... , $z_{q-1}$ liefert, also alle Elemente von ${\rm GF}(q)$ mit Ausnahme des Nullelementes $z_0 = 0$.<br> | + | *$\beta^{\hspace{0.05cm}i}$ für $1 ≤ i ≤ q- 1$ genau die Elemente $z_1$, ... , $z_{q-1}$ liefert, also alle Elemente von ${\rm GF}(q)$ mit Ausnahme des Nullelementes $z_0 = 0$.<br> |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ Von der Zahlenmenge $Z_5 = \{0, 1, 2, 3, 4\}$ sind „$2$” und „$3$” primitive Elemente wegen | + | $\text{Beispiel 3:}$ Von der Zahlenmenge $Z_5 = \{0,\ 1,\ 2,\ 3,\ 4\}$ sind „$2$” und „$3$” primitive Elemente wegen |
::<math>2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},</math> | ::<math>2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},</math> | ||
::<math>3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1</math> | ::<math>3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1</math> | ||
| − | *Dagegen ist „$4$” kein primitives Element, weil bereits $4^2 = 1$ ist: | + | *Dagegen ist „$4$” kein primitives Element, weil bereits„ $4^2 = 1$„ ist: |
::<math>4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.</math>}}<br> | ::<math>4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.</math>}}<br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Ein irreduzibles Polynom bezeichnet man gleichzeitig als ein '''primitives Polynom''', wenn die Wurzel $\alpha$ bezüglich des Polynoms $p(x)$ ein primitives Element von ${\rm GF}(q)$ ist. Dann gilt | + | $\text{Definition:}$ Ein irreduzibles Polynom bezeichnet man gleichzeitig als ein '''primitives Polynom''', wenn die Wurzel $\alpha$ bezüglich des Polynoms $p(x)$ ein primitives Element von ${\rm GF}(q)$ ist. Dann gilt |
| − | ::<math>{\rm GF}(q) = \{\hspace{0.1cm}\alpha^{-\infty} = 0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0. | + | ::<math>{\rm GF}(q) = \{\hspace{0.1cm}\alpha^{-\infty} = 0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.2cm} |
| − | \alpha\hspace{0.05cm},\hspace{0. | + | \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^{2},\hspace{0.2cm} \text{...} \hspace{0.1cm} , \hspace{0.2cm}\alpha^{q-2}\hspace{0.1cm}\}\hspace{0.05cm}. </math>}}<br> |
| − | *Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv. Ist $p_1(x)$ ein primitives Polynom, so ist auch das dazu reziproke Polynom $p_2 (x) = x^m \cdot p_1(x^{-1})$ primitiv. | + | *Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv. |
| − | *Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für $m = 3$: | + | *Ist $p_1(x)$ ein primitives Polynom, so ist auch das dazu reziproke Polynom $p_2 (x) = x^m \cdot p_1(x^{-1})$ primitiv. |
| + | *Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für $m = 3$: | ||
| − | ::<math>p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot [x^{-3} + x^{-1} + 1 ]= x^3 + x^2 + 1 \hspace{0.05cm}.</math> | + | ::<math>p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot \big[x^{-3} + x^{-1} + 1 \big]= x^3 + x^2 + 1 \hspace{0.05cm}.</math> |
*Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.<br> | *Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.<br> | ||
| Zeile 342: | Zeile 352: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ Zur Verdeutlichung dieser Aussagen betrachten wir beispielhaft | $\text{Beispiel 4:}$ Zur Verdeutlichung dieser Aussagen betrachten wir beispielhaft | ||
| − | *das Galoisfeld $\rm GF(2^3) = GF(8)$, sowie <br> | + | *das Galoisfeld $\rm GF(2^3) = GF(8)$, sowie <br> |
| − | *das Polynom $p(x) = x^3 + x + 1$.<br><br> | + | *das Polynom $p(x) = x^3 + x + 1$.<br><br> |
| − | Aus der Bedingung $p(\alpha) = 0$ erhält man in $\rm GF(2^3)$ weiter: | + | Aus der Bedingung $p(\alpha) = 0$ erhält man in $\rm GF(2^3)$ weiter: |
::<math>\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},</math> | ::<math>\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},</math> | ||
| − | und damit für die Potenzen $\alpha^{i}$ der Wurzel für $i ≥ 4$: | + | und damit für die Potenzen $\alpha^{i}$ der Wurzel für $i ≥ 4$: |
::<math>\alpha^4 = \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},</math> | ::<math>\alpha^4 = \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},</math> | ||
| Zeile 359: | Zeile 369: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 5:}$ Die Elemente $z_0$, $z_1$, ... , $z_7$ des Galoisfeldes $\rm GF(2^3)$ lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen: | + | $\text{Beispiel 5:}$ Die Elemente $z_0$, $z_1$, ... , $z_7$ des Galoisfeldes $\rm GF(2^3)$ lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen: |
| − | [[Datei:P ID2568 KC T 2 2 S4b.png|right|frame|Elemente von $\rm GF(2^3)$ in drei verschiedenen Darstellungen]] | + | [[Datei:P ID2568 KC T 2 2 S4b.png|right|frame|Elemente von $\rm GF(2^3)$ in drei verschiedenen Darstellungen]] |
| − | *als Potenzen von $\alpha$ ⇒ '''Exponentendarstellung''',<br> | + | *als Potenzen von $\alpha$ ⇒ '''Exponentendarstellung''',<br> |
| − | *als Polynome der Form $k_2 \cdot \alpha^2 + k_1 \cdot \alpha + k_0$ mit binären Koeffizienten $k_2$, $k_1$, $k_0$ | + | *als Polynome der Form $k_2 \cdot \alpha^2 + k_1 \cdot \alpha + k_0$ mit binären Koeffizienten $k_2$, $k_1$, $k_0$ ⇒ '''Polynomdarstellung''',<br> |
| − | *als Vektoren der Koeffizienten $(k_2, \ k_1, \ k_0)$ ⇒ '''Koeffizientendarstellung'''.<br><br> | + | *als Vektoren der Koeffizienten $(k_2, \ k_1, \ k_0)$ ⇒ '''Koeffizientendarstellung'''.<br><br> |
| − | Für Addition (oder Subtraktion) zweier Elemente eignen sich Polynom– und Vektordarstellung gleichermaßen, wobei die Komponenten modulo 2 zu addieren sind, zum Beispiel: | + | Für Addition (oder Subtraktion) zweier Elemente eignen sich Polynom– und Vektordarstellung gleichermaßen, wobei die Komponenten $\text{modulo 2}$ zu addieren sind, zum Beispiel: |
::<math>z_5 + z_7 =(\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},</math> | ::<math>z_5 + z_7 =(\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},</math> | ||
| Zeile 374: | Zeile 384: | ||
Für Multiplikationen ist die Exponentendarstellung gut geeignet, wie folgende Beispiele zeigen: | Für Multiplikationen ist die Exponentendarstellung gut geeignet, wie folgende Beispiele zeigen: | ||
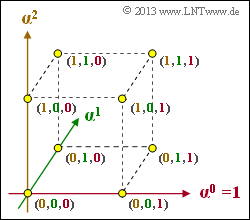
| − | [[Datei:P ID2577 KC T 2 2 S4c.png|right|frame|$\rm GF(2^3)$ in 3D–Darstellung]] | + | [[Datei:P ID2577 KC T 2 2 S4c.png|right|frame|$\rm GF(2^3)$ in 3D–Darstellung]] |
::<math>z_3 \cdot z_4 =\alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},</math> | ::<math>z_3 \cdot z_4 =\alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},</math> | ||
::<math>z_0 \cdot z_5 =\alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},</math> | ::<math>z_0 \cdot z_5 =\alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},</math> | ||
| Zeile 380: | Zeile 390: | ||
= 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.</math> | = 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.</math> | ||
| − | Man erkennt, dass sich die Exponenten modulo $q-1$ ergeben (im Beispiel modulo $7$ | + | Man erkennt, dass sich die Exponenten modulo $q-1$ ergeben $($im Beispiel modulo $7)$.<br> |
| − | Die Grafik zeigt den endlichen Erweiterungskörper $\rm GF(2^3)$ in einer 3D–Darstellung: | + | Die untere Grafik zeigt den endlichen Erweiterungskörper $\rm GF(2^3)$ in einer 3D–Darstellung: |
| − | *Die Achsen sind mit $\alpha^0 =1$, $\alpha^1$ und $\alpha^2$ bezeichnet. | + | *Die Achsen sind mit $\alpha^0 =1$, $\alpha^1$ und $\alpha^2$ bezeichnet. |
| − | *Die $2^3 = 8$ Punkte im 3D–Raum sind mit den Koeffizientenvektoren beschriftet. | + | *Die $2^3 = 8$ Punkte im 3D–Raum sind mit den Koeffizientenvektoren beschriftet. |
| − | *Die Zuordnung der Koeffizienten $k_2$, $k_1$, $k_0$ zu den Achsen ist farblich deutlich gemacht. }} | + | *Die Zuordnung der Koeffizienten $k_2$, $k_1$, $k_0$ zu den Achsen ist farblich deutlich gemacht. }} |
Aktuelle Version vom 20. Mai 2019, 10:41 Uhr
Inhaltsverzeichnis
GF(22) – Beispiel eines Erweiterungskörpers
Im Abschnitt $\text{Beispiel 2}$ im Kapitel „Einige Grundlagen der Algebra” wurde bereits gezeigt, dass die endliche Zahlenmenge $\{0, 1, 2, 3\}$ ⇒ $q = 4$ nicht die Eigenschaften eines Galoisfeldes $\rm GF(4)$ erfüllt. Vielmehr ergeben sich für die Addition modulo 4 und die Multiplikation modulo 4 folgende Tabellen:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it q} = 4\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm}\text{Addition: } \left[ \begin{array}{c|cccccc} + & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 1 &2 & 3 \\ 1 & 1 & 2 &3 & 0 \\ 2 & 2 & 3 &0 & 1 \\ 3 & 3 & 0 &1 & 2 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.25cm}\text{Multiplikation: } \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 &2 & 3 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 2 & 3 \\ 2 & 0 & 2 & 0 & 2 \\ 3 & 0 & 3 & 2 & 1 \\ \end{array} \right] . $$
Für $z_i = 2$ gibt es keine multiplikative Inverse ${\rm Inv_M}(z_i)$. Dies erkennt man daran, dass kein einziges Element $z_i ∈ \{0, 1, 2, 3\}$ die Bedingung $2 · z_i = 1$ erfüllt.
Geht man dagegen vom binären Galoisfeld ${\rm GF}(2) = \{0, 1\}$ aus und erweitert dieses entsprechend der Gleichung
- \[{\rm GF}(2^2)= \big\{k_0+k_1\cdot \alpha \ \big | \ k_0, k_1\in{\rm GF}(2) = \{ 0, 1\} \big \}\hspace{0.05cm}, \]
so ergibt sich die ebenfalls endliche Menge $\{0, 1, \alpha, 1 + \alpha\}$ ⇒ die Ordnung ist weiterhin $q=4$.
Führt man die Rechenoperationen modulo $p(\alpha) = \alpha^2 + \alpha + 1$ durch, so erhält man das folgende Ergebnis:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
Hierzu ist anzumerken:
- Die neutralen Elemente der Addition bzw. Multiplikation sind weiterhin $N_{\rm A} = 0$ und $N_{\rm M} = 1$.
- Da bei Modulo–Ausführung kein Unterschied zwischen Addition und Subtraktion besteht, ist $\alpha + \alpha = \alpha - \alpha = 0$.
- Für alle $z_i$ gilt somit: Die additive Inverse von $z_i$ ist das Element $z_i$ selbst.
- Die Einträge in der Multiplikationstabelle ergeben sich nach folgenden Berechnungen:
- \[\big [ \alpha \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + \alpha) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1\hspace{0.05cm},\]
- \[\big [ \alpha \cdot \alpha \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 ) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= 1+\alpha\hspace{0.05cm},\]
- \[\big [ (1+\alpha) \cdot (1+\alpha) \big ] \hspace{0.15cm}{\rm mod} \hspace{0.15cm} p(\alpha) = (\alpha^2 + 1) \hspace{0.15cm}{\rm mod} \hspace{0.15cm} (\alpha^2 + \alpha + 1)= \alpha\hspace{0.05cm}.\]
- Damit existieren für alle Elemente mit Ausnahme des Nullelements die multiplikativen Inversen:
- \[{\rm Inv_M}( 1) = 1 \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(\alpha) = 1+\alpha \hspace{0.05cm},\hspace{0.2cm}{\rm Inv_M}(1+\alpha) = \alpha \hspace{0.05cm}.\]
$\text{Zwischenergebnis:}$
- Die Menge $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ stellt zusammen mit den beiden Operationen Addition und Multiplikation modulo $p(\alpha)= \alpha^2 + \alpha + 1$ ein Galoisfeld dar. Die Ordnung ist $q = 4$.
- Dieses mit $\rm GF(2^2) = GF(4)$ bezeichnete Galoisfeld erfüllt alle im vorherigen Kapitel genannten Anforderungen.
- Im Gegensatz zum Zahlenkörper $\rm GF(3) = \{0, \ 1, \ 2\}$ mit der Eigenschaft, dass $q = 3$ eine Primzahl ist, nennt man $\rm GF(2^2)$ einen Erweiterungskörper (englisch: Extension Field ).
Reduzible und irreduzible Polynome
Das Polynom $p(\alpha)$ und damit die Bestimmungsgleichung $p(\alpha) = 0$ darf nicht beliebig vorgegeben werden. Das auf der letzten Seite verwendete Polynom
- $$p(\alpha)= \alpha^2 + \alpha + 1$$
ist geeignet. Nun versuchen wir es mit einem anderen Polynom, nämlich $p(\alpha)= \alpha^2 + 1$.
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm}{\it p}(\alpha)= \alpha^2 + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1 &1\!+\!\alpha \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1\!+\!\alpha & 0 \end{array} \right] .$$
Die Additionstabelle ist in beiden Fällen identisch und auch die Multiplikationstabellen unterscheiden sich nur durch die vier Einträge in den beiden unteren Zeilen und den beiden hinteren Spalten:
- Aus $p(\alpha) = 0$ folgt nun für das Produkt $\alpha \cdot \alpha = 1$ und das Produkt $(1 +\alpha) \cdot (1 +\alpha) $ ergibt das Nullelement. Das gemischte Produkt ist $\alpha \cdot (1 +\alpha) = 1 +\alpha $.
- In der letzten Zeile der Multiplikationstabelle und auch in der letzten Spalte steht nun keine „$1$” ⇒ Hinsichtlich der Bedingung $p(\alpha)= \alpha^2 + 1= 0$ existiert demzufolge die multiplikative Inverse zu $1 +\alpha$ nicht.
- Damit erfüllt aber die endliche Menge $\{0, \ 1, \ \alpha, \ 1 + \alpha\}$ zusammen mit Rechenoperationen modulo $p(\alpha)= \alpha^2 + 1$ auch nicht die Voraussetzungen eines Erweiterungskörpers $\rm GF(2^2) $.
$\text{Fassen wir zusammen:}$
Aus dem binären Galoisfeld $\rm GF(2) = \{0, \ 1\}$ lässt sich unter Zuhilfenahme eines Polynoms vom Grad $m = 2$ mit binären Koeffizienten,
- \[p(x) = x^2 + k_1 \cdot x + k_0 \hspace{0.05cm}, \hspace{0.45cm}k_0\hspace{0.05cm},\hspace{0.1cm}k_1 \in \{0, 1\} \hspace{0.05cm},\]
ein Erweiterungskörper $\rm GF(2^2)$ formulieren. Anmerkung: Die Umbenennung der Variablen $\alpha$ in $x$ hat nur formale Bedeutung im Hinblick auf spätere Seiten.
- Im vorliegenden Fall gibt es nur ein geeignetes Polynom $p_1(x)= x^2 + x + 1$. Alle anderen möglichen Polynome vom Grad $m = 2$, nämlich
- \[p_2(x) = x^2 + 1 \hspace{0.06cm} = (x+1) \cdot (x+1)\hspace{0.05cm},\]
- \[p_3(x) =x^2 \hspace{0.76cm} = x \cdot x \hspace{0.05cm},\]
- \[p_4(x) = x^2 + x = (x+1) \cdot x\hspace{0.05cm}, \]
- lassen sich faktorisieren und ergeben keinen Erweiterungskörper.
- Man nennt die Polynome $p_2(x)$, $p_3(x)$ und $p_4(x)$ reduzibel.
- Der Schluss liegt nahe, dass für einen Erweiterungskörper nur irreduzible Polynome wie $p_1(x)$ geeignet sind.
Interpretation des neuen Elementes „alpha”
Wir betrachten weiterhin den Körper ${\rm GF}(2^2) = \{0, \ 1,\ \alpha,\ 1 + \alpha\}$ entsprechend den beiden folgenden Operationstabellen, basierend auf der Nebenbedingung $p(\alpha)= \alpha^2 + \alpha + 1 = 0$ (irreduzibles Ploynom):
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c|cccccc} + & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 1 & \alpha & 1\!+\!\alpha \\ 1 & 1 & 0 & 1\!+\!\alpha & \alpha \\ \alpha & \alpha & 1\!+\!\alpha & 0 & 1 \\ 1\!+\!\alpha & 1\!+\!\alpha & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c|cccccc} \cdot & 0 & 1 & \alpha & 1\!+\!\alpha \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & 1\!+\!\alpha \\ \alpha & 0 & \alpha & 1\!+\!\alpha & 1 \\ 1\!+\!\alpha & 0 & 1\!+\!\alpha & 1 & \alpha \end{array} \right] .$$
Welche Bedeutung hat aber nun das neue Element $\alpha$?
- Das Polynom $p(\alpha)= \alpha^2 + \alpha + 1 $ hat in ${\rm GF}(2) = \{0, \ 1\}$ keine Nullstelle. Das bedeutet weiter, dass $\alpha$ weder $0$ noch $1$ sein kann.
- Wäre $\alpha= 0$ bzw. $\alpha= 1$, so wären zudem zwei der vier Mengenelemente $\{0,\ 1,\ \alpha,\ 1 + \alpha\}$ jeweils identisch: Entweder „$0$” und „$\alpha$” sowie „$1$” und „$1+\alpha$” oder „$1$” und „$\alpha$” sowie „$0$” und „$1+\alpha$”.
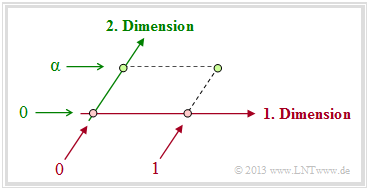
- Vielmehr erhält der eindimensionale Körper ${\rm GF}(2)$ durch die Einführung des Elementes $\alpha$ eine zweite Dimension. Er wird also zum Galoisfeld ${\rm GF}(2^2)$ erweitert, wie die nebenstehende Grafik zeigt.
- Das Element $\alpha$ hat ähnliche Bedeutung wie die imaginäre Einheit ${\rm j}$, durch die man die Menge der reellen Zahlen unter der Nebenbedingung ${\rm j}^2 + 1 = 0$ zur Menge der komplexen Zahlen erweitert.
$\text{Übliche Darstellung des binären Erweiterungskörpers}\ {\rm GF}(2^2)\text{:}$
Aufgrund der Identität $\alpha^2 = 1 + \alpha$, die aus der Nebenbedingung $p(\alpha) = 0$ folgt, kann man in gleicher Weise ${\rm GF}(2^2) = \{0,\ 1,\ \alpha,\ \alpha^2\}$ schreiben, wobei nun folgende Operationstabellen gelten:
- $$ \begin{array}{c} {\rm modulo}\hspace{0.15cm} p(\alpha)= \alpha^2 + \alpha + 1\\ \end{array}\hspace{0.25cm} \Rightarrow\hspace{0.25cm} \left[ \begin{array}{c | cccccc} + & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 1 & \alpha & \alpha^2 \\ 1 & 1 & 0 & \alpha^2 & \alpha \\ \alpha & \alpha & \alpha^2 & 0 & 1 \\ \alpha^2 & \alpha^2 & \alpha & 1 & 0 \end{array} \right] \hspace{-0.1cm} ,\hspace{0.5cm} \left[ \begin{array}{c | cccccc} \cdot & 0 & 1 & \alpha & \alpha^2 \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & \alpha & \alpha^2 \\ \alpha & 0 & \alpha &\alpha^2 & 1 \\ \alpha^2 & 0 & \alpha^2 & 1 & \alpha \end{array} \right] .$$
Polynome über einem endlichen Körper
$\text{Definition:}$ Ein Polynom in einem endlichen Körper ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt, hat folgende Form:
- \[a(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_0 + a_1 \cdot x + a_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + a_m \cdot x^{m} \hspace{0.05cm}.\]
Anzumerken ist:
- Alle Koeffizienten $a_i $ sind Elemente des Körpers: $a_i \in {\rm GF}(P)$.
- Ist der führende Koeffizient $a_m ≠ 0$, so gibt $m$ den Grad des Polynoms an.
Betrachten wir ein dazu zweites Polynom mit Grad $M$,
- \[b(x) = \sum_{i = 0}^{M} b_i \cdot x^{i} = b_0 + b_1 \cdot x + b_2 \cdot x^2 + \hspace{0.1cm}\text{...} \hspace{0.1cm} + b_M \cdot x^{M} \hspace{0.05cm},\]
so erhält man für die Summe (bzw. Differenz) und das Produkt jeweils in ${\rm GF}(P)$:
- \[a(x) \pm b(x) = \sum_{i = 0}^{{\rm max}\hspace{0.05cm}(m, \hspace{0.05cm}M)} \hspace{0.15cm}(a_i \pm b_i) \cdot x^{i} \hspace{0.05cm},\]
- \[a(x) \cdot b(x) = \sum_{i = 0}^{m + M} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
$\text{Beispiel 1:}$ Es gelte $a(x) = x^3 + x + 1$ und $b(x) = x^2 + x + 1$.
Im binären Galoisfeld ⇒ ${\rm GF}(2)$ ergibt sich nach den obigen Gleichungen für die Summe, die Differenz und das Produkt der beiden Polynome:
- \[s(x) = a(x) + b(x) = x^3 + x^2 \hspace{0.05cm}, \]
- \[d(x) = a(x) - b(x) = x^3 + x^2 = s(x)\hspace{0.05cm},\]
- \[c(x) = a(x) \cdot b(x) =\sum_{i = 0}^{3 + 2} \hspace{0.15cm}c_i \cdot x^{i}\hspace{0.05cm},\hspace{0.5cm} c_i = \sum_{j = 0}^{i}\hspace{0.15cm}a_j \cdot b_{i-j} \hspace{0.05cm}.\]
Mit $a_0 = a_1 = a_3 = b_0 = b_1 =b_2 = 1$ und $a_2 = a_4 = a_5 = b_3 = b_4 =b_5 = 0$ erhält man:
- \[c_0 = a_0 \cdot b_0 = 1 \cdot 1 = 1 \hspace{0.05cm},\]
- \[c_1 = a_0 \cdot b_1 + a_1 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_2 =a_0 \cdot b_2 + a_1 \cdot b_1 + a_2 \cdot b_0 = 1 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_3 = a_0 \cdot b_3 + a_1 \cdot b_2 + a_2 \cdot b_1 + a_3 \cdot b_0 = 1 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 1 \cdot 1 = 0 \hspace{0.05cm},\]
- \[c_4=a_0 \cdot b_4 + a_1 \cdot b_3 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ \hspace{0.05cm}a_4 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 1 + 1 \cdot 1 + 0 \cdot 1 = 1 \hspace{0.05cm},\]
- \[c_5 = a_0 \cdot b_5 + a_1 \cdot b_4 + \hspace{0.05cm}\text{...}\hspace{0.05cm}+ \hspace{0.05cm} a_5 \cdot b_0 =1 \cdot 0 + 1 \cdot 0 + 0 \cdot 0 + 1 \cdot 1 + 0 \cdot 1 + 0 \cdot 1= 1 \]
- \[\Rightarrow \hspace{0.3cm} c(x) = x^5 + x^4 +1 \hspace{0.05cm}.\]
Im Galoisfeld ${\rm GF}(3)$ erhält man aufgrund der Modulo–3–Operationen andere Ergebnisse:
- \[s(x) = (x^3 + x + 1) + (x^2 + x + 1) = x^3 + x^2 + 2x + 2\hspace{0.05cm},\]
- \[d(x) = (x^3 + x + 1) - (x^2 + x + 1) = x^3 + 2x^2 \hspace{0.05cm},\]
- \[c(x) = (x^3 + x + 1) \cdot (x^2 + x + 1) = x^5 + x^4 + 2x^3 + 2x^2 + 2x +1\hspace{0.05cm}.\]
$\text{Definition:}$ Ein Polynom $a(x)$ bezeichnet man als reduzibel (englisch: reducible), wenn es als Produkt zweier Polynome $p(x)$ und $q(x)$ mit jeweils niedrigerem Grad dargestellt werden kann:
- \[a(x) = p(x) \cdot q(x) \hspace{0.05cm}.\]
Ist diese Faktorisierung nicht möglich, das heißt, wenn
- \[a(x) = p(x) \cdot q(x) + r(x)\hspace{0.05cm},\hspace{0.5cm} r(x) \ne 0\]
gilt, so spricht man von einem irreduziblen (englisch: irreducible oder prime) Polynom.
$\text{Beispiel 2:}$ Es gelte $b(x) = x^3 + x + 1$, $p_1(x) = x^2 + x + 1$ und $p_2(x) = x^2 + 1$.
Die Grafik verdeutlicht links die Modulo–2–Multiplikation $a(x)= b(x) \cdot p_1(x)$. Das Ergebnis ist $a(x) = x^5 + x^4 + 1$.
Im rechten Teil der obigen Grafik ist die Modulo–2–Division $q(x)= a(x)/ p_2(x)$ mit dem Ergebnis $q(x) = x^3 + x^2 + x + 1$ dargestellt. Es verbleibt der Rest $r(x) = x$. Allein nach dieser Rechnung könnte $a(x) = x^5 + x^4 + 1$ durchaus ein irreduzibles Polynom sein.
Der Nachweis, dass das Polynom $a(x) = x^5 + x^4 + 1$ tatsächlich irreduzibel ist, wäre allerdings erst dann erbracht, wenn $a(x)/p(x)$ für alle
- \[p(x) = \sum_{i = 0}^{m} a_i \cdot x^{i} = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}\]
einen Rest $r(x) ≠ 0$ liefert. Dies würde im vorliegenden Beispiel (nahezu) $2^5 = 32$ Divisionen erfordern.
Aufgrund unserer linken Berechnung können wir hier sofort erkennen, dass $a(x)$ mit Sicherheit kein irreduzibles Polynom ist, da zum Beispiel $a(x) = x^5 + x^4 + 1$ dividiert durch $p_1(x) = x^2 + x + 1$ das Polynom $b(x) = x^3 + x + 1$ ohne Rest ergibt.
Verallgemeinerte Definition eines Erweiterungskörpers
Wir gehen von folgenden Voraussetzungen aus:
- einem Galoisfeld ${\rm GF}(P)$, wobei $P$ eine Primzahl angibt,
- einem irreduziblen Polynom $p(x)$ über ${\rm GF}(P)$ vom Grad $m$:
- \[p(x) = a_m \cdot x^{m} + a_{m-1} \cdot x^{m-1} + \hspace{0.1cm}\text{...} \hspace{0.1cm}+ a_2 \cdot x^2 + a_1 \cdot x + a_0 \hspace{0.05cm}, \hspace{0.3cm} a_i \in {\rm G}(P)\hspace{0.05cm}, \hspace{0.15cm}a_m \ne 0\hspace{0.05cm}. \]
Mit den genannten Voraussetzungen gilt allgemein:
$\text{Definition:}$ Es sei $P$ eine Primzahl, $m$ ganzzahlig, $p(x)$ ein irreduzibles Polynom vom Grad $m$ und es gelte $p(\alpha) = 0$.
Ein Erweiterungskörper lässt sich dann wie folgt beschreiben.
- \[{\rm GF}(P^m)= \Big\{ k_{m-1} \hspace{0.01cm}\cdot \hspace{0.02cm}\alpha^{m-1} \hspace{0.05cm}+ \hspace{0.05cm}\text{...} \hspace{0.05cm}+ \hspace{0.05cm}k_1 \hspace{0.01cm}\cdot \hspace{0.02cm} \alpha \hspace{0.05cm}+ \hspace{0.05cm} k_0\hspace{0.05cm} \Big{\vert}\hspace{0.02cm} \ k_i\in{\rm GF}(P) = \{ 0, 1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, P-1\}\Big \}.\]
- Die Addition und Multiplikation in diesem Erweiterungskörper entspricht dann der Polynom–Addition und Polynom–Multiplikation modulo $p(\alpha)$.
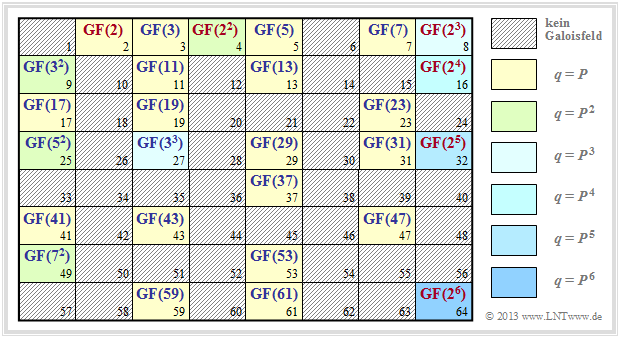
- Ein Galoisfeld ${\rm GF}(q)$ mit $q$ Elementen lässt sich also immer dann angeben, wenn die Elementenanzahl in der Form $q = P^m$ geschrieben werden kann
$(P$ kennzeichnet eine Primzahl, $m$ sei ganzzahlig$)$.
Die Grafik zeigt, für welche $q$–Werte sich jeweils ein Galoisfeld konstruieren lässt. Für die schraffiert eingezeichneten Werte ist kein endlicher Körper angebbar.
Weiter ist anzumerken:
- Die gelb hinterlegten Positionen $q=P$ ⇒ $m = 1$ markieren Zahlenmengen $\{0,\ 1,\hspace{0.05cm}\text{ ...} \hspace{0.05cm},\ q- 1\}$ mit Galoiseigenschaften, siehe Seite Definition eines Galoisfeldes.
- Die anderen Hinterlegungsfarben markieren Erweiterungskörper mit $q=P^m$, $m ≥ 2$. Für $q ≤ 64$ basieren diese auf den Primzahlen $2$, $3$, $5$ und $7$.
- Mit roter Schrift hervorgehoben sind binäre Körper ⇒ $q=2^m$, $m ≥ 1$, die auf der nächsten Seite noch genauer betrachtet werden. Alle anderen Erweiterungskörper sind blau beschriftet.
Binäre Erweiterungskörper – Primitive Polynome
Im Folgenden betrachten wir binäre Erweiterungskörper mit
- \[q = 2^m \hspace{0.15cm}(m \ge 2) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} q = 4,\ 8,\ 16, 32,\ 64,\ \text{...}\]
Elementen.
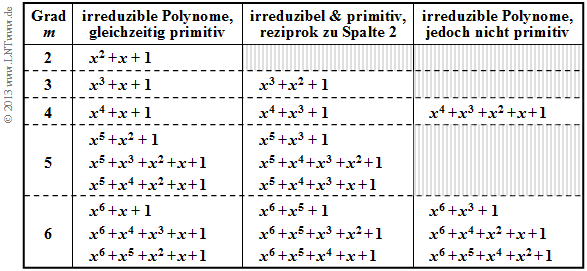
- In der Tabelle sind für $2 ≤ m ≤ 6$ alle irreduziblen Polynome des Galoisfeldes ${\rm GF}(2)$ angegeben.
- Die Polynome in Spalte 2 und 3 sind nicht nur irreduzibel, sondern zusätzlich auch primitiv.
- Primitive Polynome liefern auch die Grundlage für die Realisierung von Pseudo–Noise–Generatoren.
Bevor wir uns der Definition eines primitiven Polynoms zuwenden, sollen zunächst die Besonderheiten „primitiver Elemente” am Beispiel von
- \[{\rm GF}(q) = \{\hspace{0.05cm}z_0 = 0,\hspace{0.1cm} z_1 = 1,\hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.05cm}z_{q-1}\}\]
genannt werden. Das Element $z_i = \beta$ wird dann als primitiv bezeichnet,
- wenn die Potenz $\beta^{\hspace{0.05cm}i}$ modulo $q$ zum ersten Mal für $i = q-1$ zum Ergebnis „$1$” führt, so dass
- $\beta^{\hspace{0.05cm}i}$ für $1 ≤ i ≤ q- 1$ genau die Elemente $z_1$, ... , $z_{q-1}$ liefert, also alle Elemente von ${\rm GF}(q)$ mit Ausnahme des Nullelementes $z_0 = 0$.
$\text{Beispiel 3:}$ Von der Zahlenmenge $Z_5 = \{0,\ 1,\ 2,\ 3,\ 4\}$ sind „$2$” und „$3$” primitive Elemente wegen
- \[2^1 \hspace{-0.1cm} = \hspace{-0.1cm} 2\hspace{0.05cm},\hspace{0.2cm} 2^2 = 4\hspace{0.05cm},\hspace{0.2cm} 2^3 = 8 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},\hspace{0.2cm} 2^4 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\]
- \[3^1 \hspace{-0.1cm} = \hspace{-0.1cm} 3\hspace{0.05cm},\hspace{0.2cm} 3^2 = 9\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 3^3 = 27 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm} 3^4 = 81 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\]
- Dagegen ist „$4$” kein primitives Element, weil bereits„ $4^2 = 1$„ ist:
- \[4^1 = 4\hspace{0.05cm},\hspace{0.2cm} 4^2 = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},\hspace{0.2cm} 4^3 = 64 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4\hspace{0.05cm},\hspace{0.2cm} 4^4 = 256 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm}.\]
$\text{Definition:}$ Ein irreduzibles Polynom bezeichnet man gleichzeitig als ein primitives Polynom, wenn die Wurzel $\alpha$ bezüglich des Polynoms $p(x)$ ein primitives Element von ${\rm GF}(q)$ ist. Dann gilt
- \[{\rm GF}(q) = \{\hspace{0.1cm}\alpha^{-\infty} = 0\hspace{0.05cm},\hspace{0.1cm} \alpha^{0} = 1,\hspace{0.05cm}\hspace{0.2cm} \alpha\hspace{0.05cm},\hspace{0.2cm} \alpha^{2},\hspace{0.2cm} \text{...} \hspace{0.1cm} , \hspace{0.2cm}\alpha^{q-2}\hspace{0.1cm}\}\hspace{0.05cm}. \]
- Alle in Spalte 2 der obigen Tabelle angegebenen Polynome sind sowohl irreduzibel als auch primitiv.
- Ist $p_1(x)$ ein primitives Polynom, so ist auch das dazu reziproke Polynom $p_2 (x) = x^m \cdot p_1(x^{-1})$ primitiv.
- Alle Polynome in Spalte 3 sind reziprok zum Polynom in Spalte 2. Beispielsweise gilt für $m = 3$:
- \[p_1(x) = x^3 + x + 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}p_2(x) = x^3 \cdot \big[x^{-3} + x^{-1} + 1 \big]= x^3 + x^2 + 1 \hspace{0.05cm}.\]
- Die irreduziblen Polynome der Spalte 4 sind dagegen nicht primitiv; sie spielen nur eine untergeordnete Rolle zur Beschreibung von Fehlerkorrekturverfahren.
$\text{Beispiel 4:}$ Zur Verdeutlichung dieser Aussagen betrachten wir beispielhaft
- das Galoisfeld $\rm GF(2^3) = GF(8)$, sowie
- das Polynom $p(x) = x^3 + x + 1$.
Aus der Bedingung $p(\alpha) = 0$ erhält man in $\rm GF(2^3)$ weiter:
- \[\alpha^3 + \alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\alpha^3 = \alpha + 1 \hspace{0.05cm},\]
und damit für die Potenzen $\alpha^{i}$ der Wurzel für $i ≥ 4$:
- \[\alpha^4 = \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},\]
- \[\alpha^5 = \alpha^2 \cdot \alpha^3 = \alpha^2 \cdot (\alpha + 1) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1 \hspace{0.05cm},\]
- \[\alpha^6 = \alpha^3 \cdot \alpha^3 = (\alpha + 1) \cdot (\alpha + 1) = \alpha^2 + \alpha + \alpha + 1= \alpha^2 + 1 \hspace{0.05cm},\]
- \[\alpha^7 = \alpha^4 \cdot \alpha^3 = (\alpha^2 + \alpha) \cdot (\alpha + 1) = \alpha^3 + \alpha^2 + \alpha^2 + \alpha = \alpha + 1 + \alpha = 1 = \alpha^0 \hspace{0.05cm}.\]
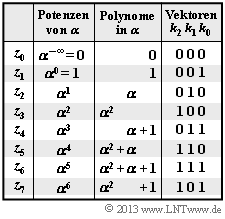
$\text{Beispiel 5:}$ Die Elemente $z_0$, $z_1$, ... , $z_7$ des Galoisfeldes $\rm GF(2^3)$ lassen sich entsprechend der nebenstehenden Tabelle wie folgt darstellen:
- als Potenzen von $\alpha$ ⇒ Exponentendarstellung,
- als Polynome der Form $k_2 \cdot \alpha^2 + k_1 \cdot \alpha + k_0$ mit binären Koeffizienten $k_2$, $k_1$, $k_0$ ⇒ Polynomdarstellung,
- als Vektoren der Koeffizienten $(k_2, \ k_1, \ k_0)$ ⇒ Koeffizientendarstellung.
Für Addition (oder Subtraktion) zweier Elemente eignen sich Polynom– und Vektordarstellung gleichermaßen, wobei die Komponenten $\text{modulo 2}$ zu addieren sind, zum Beispiel:
- \[z_5 + z_7 =(\alpha^2 + \alpha) + (\alpha^2 + 1) = \alpha + 1 = \alpha^3 = z_4 \hspace{0.05cm},\]
- \[{\rm oder}\hspace{0.15cm} z_5 + z_7 =(110) + (101) = (011) = z_4 \hspace{0.05cm},\]
- \[\hspace{0.15cm} z_1 + z_2 + z_3 =(001) + (010) + (100)= (111) = z_6 \hspace{0.05cm}.\]
Für Multiplikationen ist die Exponentendarstellung gut geeignet, wie folgende Beispiele zeigen:
- \[z_3 \cdot z_4 =\alpha^2 \cdot \alpha^3 = \alpha^{2+3}= \alpha^{5} = z_6 \hspace{0.05cm},\]
- \[z_0 \cdot z_5 =\alpha^{-\infty} \cdot \alpha^4 = \alpha^{-\infty} = z_0 \hspace{0.05cm},\]
- \[z_5 \cdot z_7 = \alpha^4 \cdot \alpha^6 = \alpha^{10}= \alpha^{7} \cdot \alpha^{3} = 1 \cdot \alpha^{3}= z_4 \hspace{0.05cm}.\]
Man erkennt, dass sich die Exponenten modulo $q-1$ ergeben $($im Beispiel modulo $7)$.
Die untere Grafik zeigt den endlichen Erweiterungskörper $\rm GF(2^3)$ in einer 3D–Darstellung:
- Die Achsen sind mit $\alpha^0 =1$, $\alpha^1$ und $\alpha^2$ bezeichnet.
- Die $2^3 = 8$ Punkte im 3D–Raum sind mit den Koeffizientenvektoren beschriftet.
- Die Zuordnung der Koeffizienten $k_2$, $k_1$, $k_0$ zu den Achsen ist farblich deutlich gemacht.
Aufgaben zum Kapitel
Aufgabe 2.3: Reduzible und irreduzible Polynome
Aufgabe 2.4: $\rm GF(2^2)$–Darstellungsformen
Aufgabe 2.4Z: Endliche und unendliche Körper
Aufgabe 2.5: Drei Varianten von $\rm GF(2^4)$
Aufgabe 2.5Z: Einige Berechnungen über $\rm GF(2^3)$
Aufgabe 2.6: ${\rm GF}(P^m)$. Welches $P$, welches $m$?