Aufgaben:Aufgabe 3.3: Momente bei cos²-WDF: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
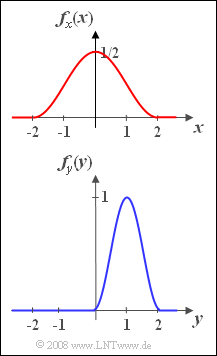
| − | [[Datei:P_ID119__Sto_A_3_3.png|right|frame|Cosinus–Quadrat–WDF und ähnliche WDF]] | + | [[Datei:P_ID119__Sto_A_3_3.png|right|frame|Cosinus–Quadrat–WDF <br>und eine ähnliche WDF]] |
| − | Wie in [[Aufgaben:3.1_cos²_-_und_Dirac-WDF|Aufgabe 3.1]] und [[Aufgaben: | + | Wie in [[Aufgaben:3.1_cos²_-_und_Dirac-WDF|Aufgabe 3.1]] und [[Aufgaben:Aufgabe_3.2:_VTF_zur_Aufgabe_3.1|Aufgabe 3.2]] betrachten wir die auf den Wertebereich von $-2$ bis $+2$ beschränkte Zufallsgröße $x$ mit folgender WDF in diesem Abschnitt: |
:$$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$ | :$$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$ | ||
| − | Daneben betrachten wir eine zweite Zufallsgröße $y$ , die nur Werte zwischen $0$ und $2$ mit folgender WDF liefert: | + | Daneben betrachten wir eine zweite Zufallsgröße $y$, die nur Werte zwischen $0$ und $2$ mit folgender WDF liefert: |
:$$f_y(y)=\sin^2({\pi}/{2}\cdot y).$$ | :$$f_y(y)=\sin^2({\pi}/{2}\cdot y).$$ | ||
*Beide Dichtefunktionen sind in der Grafik dargestellt. | *Beide Dichtefunktionen sind in der Grafik dargestellt. | ||
| − | *Außerhalb der Bereiche $-2 < x < +2$ bzw. $0 < x < +2$ gilt jeweils $f_x(x) = 0$ bzw. $f_y(y) = 0$. | + | *Außerhalb der Bereiche $-2 < x < +2$ bzw. $0 < x < +2$ gilt jeweils $f_x(x) = 0$ bzw. $f_y(y) = 0$. |
| − | *Beide Zufallsgrößen können als (normierte) Momentanwerte der zugehörigen Zufallssignale $x(t)$ bzw. $y(t)$ aufgefasst werden. | + | *Beide Zufallsgrößen können als (normierte) Momentanwerte der zugehörigen Zufallssignale $x(t)$ bzw. $y(t)$ aufgefasst werden. |
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. | |
| − | |||
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. | ||
*Für die Lösung dieser Aufgabe können Sie das folgende unbestimmte Integral benutzen: | *Für die Lösung dieser Aufgabe können Sie das folgende unbestimmte Integral benutzen: | ||
| Zeile 29: | Zeile 27: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der folgenden Aussagen treffen bei jeder beliebigen WDF $f_x(x)$ zu? | + | {Welche der folgenden Aussagen treffen bei jeder beliebigen WDF $f_x(x)$ zu? |
| − | <br>Verwendet sind folgende Größen: linearer Mittelwert $m_1$, quadratischer Mittelwert $m_2$, Varianz $\sigma^2$. | + | <br>Verwendet sind folgende Größen: linearer Mittelwert $m_1$, quadratischer Mittelwert $m_2$, Varianz $\sigma^2$. |
|type="[]"} | |type="[]"} | ||
| − | - $m_2 = 0$, falls $m_1 \ne 0$. | + | - $m_2 = 0$, falls $m_1 \ne 0$. |
| − | - $m_2 = 0$, falls $m_1 = 0$. | + | - $m_2 = 0$, falls $m_1 = 0$. |
| − | + $m_1 = 0$, falls $m_2 = 0$. | + | + $m_1 = 0$, falls $m_2 = 0$. |
| − | + $m_2 > \sigma^2$, falls $m_1 \ne 0$. | + | + $m_2 > \sigma^2$, falls $m_1 \ne 0$. |
| − | + $m_1 = 0$, falls $f_x(-x) = f_x(x)$. | + | + $m_1 = 0$, falls $f_x(-x) = f_x(x)$. |
| − | - $f_x(-x) = f_x(x)$, falls $m_1 = 0$. | + | - $f_x(-x) = f_x(x)$, falls $m_1 = 0$. |
| − | {Wie groß ist der Gleichanteil (lineare Mittelwert) des Signals $x(t)$? | + | {Wie groß ist der Gleichanteil (lineare Mittelwert) des Signals $x(t)$? |
|type="{}"} | |type="{}"} | ||
$m_x \ = \ $ { 0. } | $m_x \ = \ $ { 0. } | ||
| − | {Wie groß ist der Effektivwert des Signals $x(t)$? | + | {Wie groß ist der Effektivwert des Signals $x(t)$? |
|type="{}"} | |type="{}"} | ||
$\sigma_x \ = \ $ { 0.722 3% } | $\sigma_x \ = \ $ { 0.722 3% } | ||
| − | {Die Zufallsgröße $y$ lässt sich aus $x$ ableiten. Welche Zuordnung gilt? | + | {Die Zufallsgröße $y$ lässt sich aus $x$ ableiten. Welche Zuordnung gilt? |
| − | |type=" | + | |type="()"} |
+ $y = 1+x/2.$ | + $y = 1+x/2.$ | ||
- $y = 2x.$ | - $y = 2x.$ | ||
| Zeile 57: | Zeile 55: | ||
| − | {Wie groß ist der Gleichanteil des Signals $y(t)$? | + | {Wie groß ist der Gleichanteil des Signals $y(t)$? |
|type="{}"} | |type="{}"} | ||
$m_y\ = \ $ { 1 3% } | $m_y\ = \ $ { 1 3% } | ||
| − | {Wie groß ist der Effektivwert des Signals $y(t)$? | + | {Wie groß ist der Effektivwert des Signals $y(t)$? |
|type="{}"} | |type="{}"} | ||
$\sigma_y\ = \ $ { 0.361 3% } | $\sigma_y\ = \ $ { 0.361 3% } | ||
| Zeile 72: | Zeile 70: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Unter allen Umständen richtig sind <u>die Aussagen 3, 4 und 5</u>: | + | '''(1)''' Unter allen Umständen richtig sind <u>die Aussagen 3, 4 und 5</u>: |
| − | *Die erste Aussage ist nie erfüllt, wie aus dem | + | *Die erste Aussage ist nie erfüllt, wie aus dem "Satz von Steiner" ersichtlich ist. |
| − | *Die zweite Aussage gilt nur im Sonderfall $x = 0$. | + | *Die zweite Aussage gilt nur im (trivialen) Sonderfall $x = 0$. |
| − | Es gibt aber auch mittelwertfreie Zufallsgrößen mit unsymmetrischer WDF. Das bedeutet: Die Aussage 6 trifft nicht immer zu. | + | |
| + | |||
| + | Es gibt aber auch mittelwertfreie Zufallsgrößen mit unsymmetrischer WDF. | ||
| + | *Das bedeutet: Die Aussage 6 trifft nicht immer zu. | ||
| + | |||
| + | |||
| − | '''(2)''' Aufgrund der WDF-Symmetrie bezüglich $x = 0$ ergibt sich für den linearen Mittelwert $m_x \hspace{0.15cm}\underline{= 0}$. | + | '''(2)''' Aufgrund der WDF-Symmetrie bezüglich $x = 0$ ergibt sich für den linearen Mittelwert $m_x \hspace{0.15cm}\underline{= 0}$. |
| − | '''(3)''' Der Effektivwert des Signals $x(t)$ ist gleich der Streuung $\sigma_x$ bzw. gleich der Wurzel aus der Varianz $\sigma_x^2$. Da die Zufallsgröße $x$ den Mittelwert $m_x {= 0}$ aufweist, ist die Varianz nach dem | + | |
| + | |||
| + | '''(3)''' Der Effektivwert des Signals $x(t)$ ist gleich der Streuung $\sigma_x$ bzw. gleich der Wurzel aus der Varianz $\sigma_x^2$. | ||
| + | *Da die Zufallsgröße $x$ den Mittelwert $m_x {= 0}$ aufweist, ist die Varianz nach dem Satz von Steiner gleich dem quadratischen Mittelwert. | ||
| + | *Dieser wird in Zusammenhang mit Signalen auch als die Leistung $($bezogen auf $1 \ \rm \Omega)$ bezeichnet. Somit gilt: | ||
:$$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$ | :$$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$ | ||
| − | + | *Mit der Beziehung $\cos^2(\alpha) = 0.5 \cdot \big[1 + \cos(2\alpha)\big]$ folgt daraus: | |
| − | Mit der Beziehung $\cos^2(\alpha) = 0.5 \cdot [1 + \cos(2\alpha)]$ folgt daraus: | ||
:$$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x + \int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{2}\cdot \cos({\pi}/{\rm 2}\cdot\it x) \hspace{0.1cm} {\rm d}x.$$ | :$$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x + \int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{2}\cdot \cos({\pi}/{\rm 2}\cdot\it x) \hspace{0.1cm} {\rm d}x.$$ | ||
| − | Diese beiden Standardintegrale findet man in Tabellen. Man erhält mit $a = \pi/2$: | + | *Diese beiden Standardintegrale findet man in Tabellen. Man erhält mit $a = \pi/2$: |
:$$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} + \frac{x}{a^2}\cdot {\cos}(a x) + \left( \frac{x^{\rm2}}{{\rm2}a} - \frac{1}{a^3} \right) \cdot \sin(a \cdot x)\right]_{x=0}^{x=2} \hspace{0.5cm} | :$$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} + \frac{x}{a^2}\cdot {\cos}(a x) + \left( \frac{x^{\rm2}}{{\rm2}a} - \frac{1}{a^3} \right) \cdot \sin(a \cdot x)\right]_{x=0}^{x=2} \hspace{0.5cm} | ||
\Rightarrow \hspace{0.5cm} \sigma_{x}^{\rm 2}=\frac{\rm 4}{\rm 3}-\frac{\rm 8}{\rm \pi^2}\approx 0.524\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\sigma_x \hspace{0.15cm}\underline{\approx 0.722}.$$ | \Rightarrow \hspace{0.5cm} \sigma_{x}^{\rm 2}=\frac{\rm 4}{\rm 3}-\frac{\rm 8}{\rm \pi^2}\approx 0.524\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\sigma_x \hspace{0.15cm}\underline{\approx 0.722}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | '''(5)''' Aus der Grafik auf dem Angabenblatt ist bereits offensichtlich, dass $m_y \hspace{0.15cm}\underline{=+1}$ gelten muss. | + | '''(4)''' Richtig ist der <u>erstgenannte Vorschlag</u>: |
| + | * Die Variante $y = 2x$ würde eine zwischen $-4$ und $+4$ verteilte Zufallsgröße liefern. | ||
| + | *Beim letzten Vorschlag $y = x/2-1$ wäre der Mittelwert $m_y = -1$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Aus der Grafik auf dem Angabenblatt ist bereits offensichtlich, dass $m_y \hspace{0.15cm}\underline{=+1}$ gelten muss. | ||
| + | |||
| + | |||
| − | '''(6)''' Der Mittelwert ändert nichts an der Varianz und an der Streuung. Durch die Stauchung um den Faktor $2$ wird die Streuung gegenüber Teilaufgabe (3) ebenfalls um diesen Faktor kleiner: | + | '''(6)''' Der Mittelwert ändert nichts an der Varianz und an der Streuung. |
| + | *Durch die Stauchung um den Faktor $2$ wird die Streuung gegenüber Teilaufgabe '''(3)''' ebenfalls um diesen Faktor kleiner: | ||
:$$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$ | :$$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 5. Januar 2022, 14:59 Uhr
Wie in Aufgabe 3.1 und Aufgabe 3.2 betrachten wir die auf den Wertebereich von $-2$ bis $+2$ beschränkte Zufallsgröße $x$ mit folgender WDF in diesem Abschnitt:
- $$f_x(x)= {1}/{2}\cdot \cos^2({\pi}/{4}\cdot { x}).$$
Daneben betrachten wir eine zweite Zufallsgröße $y$, die nur Werte zwischen $0$ und $2$ mit folgender WDF liefert:
- $$f_y(y)=\sin^2({\pi}/{2}\cdot y).$$
- Beide Dichtefunktionen sind in der Grafik dargestellt.
- Außerhalb der Bereiche $-2 < x < +2$ bzw. $0 < x < +2$ gilt jeweils $f_x(x) = 0$ bzw. $f_y(y) = 0$.
- Beide Zufallsgrößen können als (normierte) Momentanwerte der zugehörigen Zufallssignale $x(t)$ bzw. $y(t)$ aufgefasst werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Erwartungswerte und Momente.
- Für die Lösung dieser Aufgabe können Sie das folgende unbestimmte Integral benutzen:
- $$\int x^{2}\cdot {\cos}(ax)\,{\rm d}x=\frac{2 x}{ a^{ 2}}\cdot \cos(ax)+ \left [\frac{x^{\rm 2}}{\it a} - \frac{\rm 2}{\it a^{\rm 3}} \right ]\cdot \rm sin(\it ax \rm ) .$$
Fragebogen
Musterlösung
- Die erste Aussage ist nie erfüllt, wie aus dem "Satz von Steiner" ersichtlich ist.
- Die zweite Aussage gilt nur im (trivialen) Sonderfall $x = 0$.
Es gibt aber auch mittelwertfreie Zufallsgrößen mit unsymmetrischer WDF.
- Das bedeutet: Die Aussage 6 trifft nicht immer zu.
(2) Aufgrund der WDF-Symmetrie bezüglich $x = 0$ ergibt sich für den linearen Mittelwert $m_x \hspace{0.15cm}\underline{= 0}$.
(3) Der Effektivwert des Signals $x(t)$ ist gleich der Streuung $\sigma_x$ bzw. gleich der Wurzel aus der Varianz $\sigma_x^2$.
- Da die Zufallsgröße $x$ den Mittelwert $m_x {= 0}$ aufweist, ist die Varianz nach dem Satz von Steiner gleich dem quadratischen Mittelwert.
- Dieser wird in Zusammenhang mit Signalen auch als die Leistung $($bezogen auf $1 \ \rm \Omega)$ bezeichnet. Somit gilt:
- $$\sigma_x^{\rm 2}=\int_{-\infty}^{+\infty}x^{\rm 2}\cdot f_x(x)\hspace{0.1cm}{\rm d}x=2 \cdot \int_{\rm 0}^{\rm 2} x^2/2 \cdot \cos^2({\pi}/4\cdot\it x)\hspace{0.1cm} {\rm d}x.$$
- Mit der Beziehung $\cos^2(\alpha) = 0.5 \cdot \big[1 + \cos(2\alpha)\big]$ folgt daraus:
- $$\sigma_x^2=\int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{\rm 2} \hspace{0.1cm}{\rm d}x + \int_{\rm 0}^{\rm 2}{x^{\rm 2}}/{2}\cdot \cos({\pi}/{\rm 2}\cdot\it x) \hspace{0.1cm} {\rm d}x.$$
- Diese beiden Standardintegrale findet man in Tabellen. Man erhält mit $a = \pi/2$:
- $$\sigma_x^{\rm 2}=\left[\frac{x^{\rm 3}}{\rm 6} + \frac{x}{a^2}\cdot {\cos}(a x) + \left( \frac{x^{\rm2}}{{\rm2}a} - \frac{1}{a^3} \right) \cdot \sin(a \cdot x)\right]_{x=0}^{x=2} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \sigma_{x}^{\rm 2}=\frac{\rm 4}{\rm 3}-\frac{\rm 8}{\rm \pi^2}\approx 0.524\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\sigma_x \hspace{0.15cm}\underline{\approx 0.722}.$$
(4) Richtig ist der erstgenannte Vorschlag:
- Die Variante $y = 2x$ würde eine zwischen $-4$ und $+4$ verteilte Zufallsgröße liefern.
- Beim letzten Vorschlag $y = x/2-1$ wäre der Mittelwert $m_y = -1$.
(5) Aus der Grafik auf dem Angabenblatt ist bereits offensichtlich, dass $m_y \hspace{0.15cm}\underline{=+1}$ gelten muss.
(6) Der Mittelwert ändert nichts an der Varianz und an der Streuung.
- Durch die Stauchung um den Faktor $2$ wird die Streuung gegenüber Teilaufgabe (3) ebenfalls um diesen Faktor kleiner:
- $$\sigma_y=\sigma_x/\rm 2\hspace{0.15cm}\underline{\approx 0.361}.$$