Aufgaben:Aufgabe 4.10Z: Korrelationsdauer: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID393__Sto_Z_4_10.png|right|frame|Musterfunktionen ergodischer Prozesse]] | [[Datei:P_ID393__Sto_Z_4_10.png|right|frame|Musterfunktionen ergodischer Prozesse]] | ||
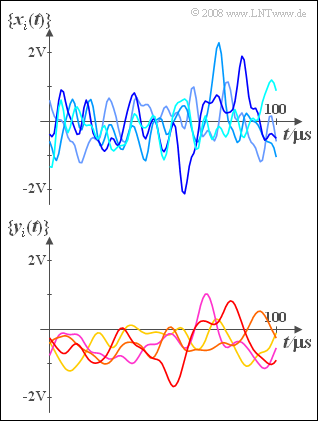
| − | Das nebenstehende Bild zeigt Mustersignale zweier Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ mit jeweils gleicher Leistung $P_x = P_y = 5\hspace{0.05 cm} \rm mW$. Vorausgesetzt ist hierbei der Widerstand $R = 50\hspace{0.05 cm}\rm \Omega$. | + | Das nebenstehende Bild zeigt Mustersignale zweier Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ mit jeweils gleicher Leistung $P_x = P_y = 5\hspace{0.05 cm} \rm mW$. Vorausgesetzt ist hierbei der Widerstand $R = 50\hspace{0.05 cm}\rm \Omega$. |
| − | Der Zufallsprozess $\{x_i(t)\}$ | + | Der Zufallsprozess $\{x_i(t)\}$ |
| − | * ist mittelwertfrei $(m_x = 0)$, | + | * ist mittelwertfrei $(m_x = 0)$, |
| − | * besitzt die gaußförmige AKF $\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$ | + | * besitzt die gaußförmige AKF $\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$ und |
| − | * | + | * weist die äquivalente AKF-Dauer $\nabla \tau_x = 5\hspace{0.05 cm}\rm µ s $ auf. |
| − | Wie aus dem unteren Bild zu erkennen ist, hat der Zufallsprozess $\{y_i(t)\}$ sehr viel stärkere innere statistische Bindungen als der Zufallsprozess $\{x_i(t)\}$. | + | Wie aus dem unteren Bild zu erkennen ist, hat der Zufallsprozess $\{y_i(t)\}$ sehr viel stärkere innere statistische Bindungen als der Zufallsprozess $\{x_i(t)\}$. |
Oder anders ausgedrückt: | Oder anders ausgedrückt: | ||
| − | *Der Zufallsprozess $\{y_i(t)\}$ ist niederfrequenter als $\{x_i(t)\}$. | + | *Der Zufallsprozess $\{y_i(t)\}$ ist niederfrequenter als $\{x_i(t)\}$. |
| − | *Die äquivalente AKF-Dauer ist $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $. | + | *Die äquivalente AKF-Dauer ist $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $. |
| − | Aus der Skizze ist auch zu erkennen, dass $\{y_i(t)\}$ im Gegensatz zu $\{x_i(t)\}$ nicht gleichsignalfrei ist. | + | Aus der Skizze ist auch zu erkennen, dass $\{y_i(t)\}$ im Gegensatz zu $\{x_i(t)\}$ nicht gleichsignalfrei ist. Der Gleichsignalanteil beträgt vielmehr $m_y = -0.3 \hspace{0.05 cm}\rm V$. |
| − | |||
| − | + | '''Hinweise:''' | |
| − | ''Hinweise:'' | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. |
| − | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Autokorrelationsfunktion]]. | + | *Bezug genommen wird insbesondere auf die Seite [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Interpretation_der_Autokorrelationsfunktion|Interpretation der Autokorrelationsfunktion]]. |
| − | *Bezug genommen wird insbesondere auf die Seite [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)#Interpretation_der_Autokorrelationsfunktion|Interpretation der Autokorrelationsfunktion]]. | ||
| Zeile 39: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welchen Effektivwert $(\sigma_x)$ besitzen die Mustersignale des Prozesses $\{x_i(t)\}$? | + | {Welchen Effektivwert $(\sigma_x)$ besitzen die Mustersignale des Prozesses $\{x_i(t)\}$? |
|type="{}"} | |type="{}"} | ||
$\sigma_x \ = \ $ { 0.5 3% } $\ \rm V$ | $\sigma_x \ = \ $ { 0.5 3% } $\ \rm V$ | ||
| − | {Welche AKF& | + | {Welche AKF–Werte ergeben sich für $\tau = 2\hspace{0.05 cm}\rm µs$ bzw. $\tau = 5\hspace{0.05 cm}\rm µ s$? |
|type="{}"} | |type="{}"} | ||
$\varphi_x(\tau = 2\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 3.025 3% } $\ \rm mW$ | $\varphi_x(\tau = 2\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 3.025 3% } $\ \rm mW$ | ||
| Zeile 50: | Zeile 48: | ||
| − | {Wie groß ist die Korrelationsdauer $T_{\rm K}$, also derjenige Zeitpunkt, bei dem die AKF auf die Hälfte des Maximums abgefallen ist? | + | {Wie groß ist die Korrelationsdauer $T_{\rm K}$, also derjenige Zeitpunkt, bei dem die AKF auf die Hälfte des Maximums abgefallen ist? |
|type="{}"} | |type="{}"} | ||
$T_{\rm K} \ = \ $ { 2.35 3% } $\ \rm µ s$ | $T_{\rm K} \ = \ $ { 2.35 3% } $\ \rm µ s$ | ||
| − | {Welchen Effektivwert $(\sigma_y)$ besitzen die Mustersignale des Prozesses $\{y_i(t)\}$? | + | {Welchen Effektivwert $(\sigma_y)$ besitzen die Mustersignale des Prozesses $\{y_i(t)\}$? |
|type="{}"} | |type="{}"} | ||
$\sigma_y \ = \ $ { 0.4 3% } $\ \rm V$ | $\sigma_y \ = \ $ { 0.4 3% } $\ \rm V$ | ||
| − | {Berechnen Sie die AKF $\varphi_x(\tau)$. Wie groß ist der AKF-Wert bei $\tau = 10\hspace{0.05 cm}\rm µ s$? | + | {Berechnen Sie die AKF $\varphi_x(\tau)$. Wie groß ist der AKF-Wert bei $\tau = 10\hspace{0.05 cm}\rm µ s$? Welcher AKF–Verlauf ergäbe sich bei positivem Mittelwert $(m_y = +0.3 \hspace{0.05 cm}\rm V)$? |
|type="{}"} | |type="{}"} | ||
$\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 1.938 3% } $\ \rm mW$ | $\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \ = \ $ { 1.938 3% } $\ \rm mW$ | ||
| Zeile 70: | Zeile 68: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Das zweite Moment ergibt sich zu $m_{2x} = R \cdot P_x = 50 \hspace{0.05 cm}{\rm \Omega}\cdot 5 \hspace{0.05 cm}{\rm mW}= 0.25 \hspace{0.05 cm}{\rm V}^2.$ |
| + | *Daraus folgt der Effektivwert $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$. | ||
| − | '''(2)''' Wegen $P_x = \varphi_x (\tau = 0)$ gilt für die AKF allgemein: | + | |
| + | '''(2)''' Wegen $P_x = \varphi_x (\tau = 0)$ gilt für die AKF allgemein: | ||
:$$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$ | :$$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$ | ||
*Daraus erhält man: | *Daraus erhält man: | ||
:$$\varphi_x (\tau = {\rm 2\hspace{0.1cm} µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$ | :$$\varphi_x (\tau = {\rm 2\hspace{0.1cm} µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$ | ||
:$$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$ | :$$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$ | ||
| + | |||
| Zeile 84: | Zeile 85: | ||
:$${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ \ln(2)}/{\pi}}\hspace{0.05cm}.$$ | :$${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ \ln(2)}/{\pi}}\hspace{0.05cm}.$$ | ||
| − | Daraus folgt $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$. Bei anderer AKF-Form erhält man ein anderes Verhältnis für $T_{\rm K} / {\rm \nabla} \tau_x$. | + | *Daraus folgt $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$. |
| + | *Bei anderer AKF-Form erhält man ein anderes Verhältnis für $T_{\rm K} / {\rm \nabla} \tau_x$. | ||
| + | |||
| − | '''(4)''' | + | |
| − | $m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$ Daraus folgt | + | '''(4)''' Die Leistungen $P_x = P_y$ sind gleich, und zwar jeweils $0.25\hspace{0.05 cm}\rm V^2$. |
| + | *Unter Berücksichtigung des Mittelwertes $m_y = -0.3 \hspace{0.05 cm}\rm V$ gilt: | ||
| + | :$$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$ | ||
| + | *Daraus folgt: | ||
:$$\sigma_y\hspace{0.15 cm}\underline{= 0.4\hspace{0.05 cm}{\rm V}}.$$ | :$$\sigma_y\hspace{0.15 cm}\underline{= 0.4\hspace{0.05 cm}{\rm V}}.$$ | ||
| − | '''(5)''' Bezogen auf den Einheitswiderstand $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ lautet die AKF des Prozesses $\{y_i(t)\}$: | + | |
| + | '''(5)''' Bezogen auf den Einheitswiderstand $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ lautet die AKF des Prozesses $\{y_i(t)\}$: | ||
:$$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$ | :$$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$ | ||
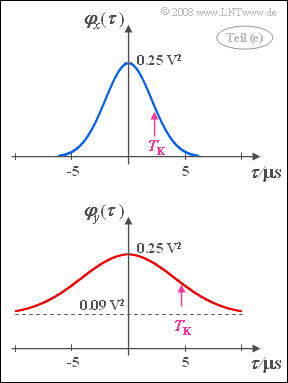
| − | Rechts sehen Sie den Funktionsverlauf. Bezogen auf den Widerstand $ R = 50 \hspace{0.05 cm}{\rm \Omega}$ ergeben sich die nachfolgend angegebenen AKF-Werte: | + | *Rechts sehen Sie den Funktionsverlauf. Bezogen auf den Widerstand $ R = 50 \hspace{0.05 cm}{\rm \Omega}$ ergeben sich die nachfolgend angegebenen AKF-Werte: |
:$$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$ | :$$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$ | ||
| − | Daraus folgt: | + | *Daraus folgt: |
:$$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2} \hspace{0.3cm }\Rightarrow \hspace{0.3cm }\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) | :$$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2} \hspace{0.3cm }\Rightarrow \hspace{0.3cm }\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) | ||
\hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$ | \hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$ | ||
| − | Bei positivem Mittelwert $m_y$ (mit gleichem Betrag) würde sich an der AKF nichts ändern, da $m_y$ in die AKF-Gleichung quadratisch eingeht. | + | *Bei positivem Mittelwert $m_y$ (mit gleichem Betrag) würde sich an der AKF nichts ändern, da $m_y$ in die AKF-Gleichung quadratisch eingeht. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 21. März 2022, 16:25 Uhr
Das nebenstehende Bild zeigt Mustersignale zweier Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$ mit jeweils gleicher Leistung $P_x = P_y = 5\hspace{0.05 cm} \rm mW$. Vorausgesetzt ist hierbei der Widerstand $R = 50\hspace{0.05 cm}\rm \Omega$.
Der Zufallsprozess $\{x_i(t)\}$
- ist mittelwertfrei $(m_x = 0)$,
- besitzt die gaußförmige AKF $\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$ und
- weist die äquivalente AKF-Dauer $\nabla \tau_x = 5\hspace{0.05 cm}\rm µ s $ auf.
Wie aus dem unteren Bild zu erkennen ist, hat der Zufallsprozess $\{y_i(t)\}$ sehr viel stärkere innere statistische Bindungen als der Zufallsprozess $\{x_i(t)\}$.
Oder anders ausgedrückt:
- Der Zufallsprozess $\{y_i(t)\}$ ist niederfrequenter als $\{x_i(t)\}$.
- Die äquivalente AKF-Dauer ist $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $.
Aus der Skizze ist auch zu erkennen, dass $\{y_i(t)\}$ im Gegensatz zu $\{x_i(t)\}$ nicht gleichsignalfrei ist. Der Gleichsignalanteil beträgt vielmehr $m_y = -0.3 \hspace{0.05 cm}\rm V$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.
- Bezug genommen wird insbesondere auf die Seite Interpretation der Autokorrelationsfunktion.
Fragebogen
Musterlösung
- Daraus folgt der Effektivwert $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$.
(2) Wegen $P_x = \varphi_x (\tau = 0)$ gilt für die AKF allgemein:
- $$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$
- Daraus erhält man:
- $$\varphi_x (\tau = {\rm 2\hspace{0.1cm} µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$
- $$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$
(3) Hier gilt folgende Bestimmungsgleichung:
- $${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ \ln(2)}/{\pi}}\hspace{0.05cm}.$$
- Daraus folgt $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$.
- Bei anderer AKF-Form erhält man ein anderes Verhältnis für $T_{\rm K} / {\rm \nabla} \tau_x$.
(4) Die Leistungen $P_x = P_y$ sind gleich, und zwar jeweils $0.25\hspace{0.05 cm}\rm V^2$.
- Unter Berücksichtigung des Mittelwertes $m_y = -0.3 \hspace{0.05 cm}\rm V$ gilt:
- $$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$
- Daraus folgt:
- $$\sigma_y\hspace{0.15 cm}\underline{= 0.4\hspace{0.05 cm}{\rm V}}.$$
(5) Bezogen auf den Einheitswiderstand $ R = 1 \hspace{0.05 cm}{\rm \Omega}$ lautet die AKF des Prozesses $\{y_i(t)\}$:
- $$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$
- Rechts sehen Sie den Funktionsverlauf. Bezogen auf den Widerstand $ R = 50 \hspace{0.05 cm}{\rm \Omega}$ ergeben sich die nachfolgend angegebenen AKF-Werte:
- $$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$
- Daraus folgt:
- $$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2} \hspace{0.3cm }\Rightarrow \hspace{0.3cm }\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$
- Bei positivem Mittelwert $m_y$ (mit gleichem Betrag) würde sich an der AKF nichts ändern, da $m_y$ in die AKF-Gleichung quadratisch eingeht.