Aufgaben:Aufgabe 1.4Z: Alles rechteckförmig: Unterschied zwischen den Versionen
Aus LNTwww
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} | ||
| − | [[Datei:P_ID834__LZI_Z_1_4.png |right|frame|Periodisches Rechtecksignal und Filter mit rechteckförmiger Impulsantwort]] | + | [[Datei:P_ID834__LZI_Z_1_4.png |right|frame|Periodisches Rechtecksignal und <br>Filter mit rechteckförmiger Impulsantwort]] |
| − | Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist. | + | Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist. |
| − | Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, | + | *Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, das heißt bei $3f_0$, $5f_0,$ usw. Zusätzlich gibt es einen Gleichanteil. |
| − | *Dazu betrachten wir zwei Filter $\rm A$ und $\rm B$ mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit der Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$. | + | *Dazu betrachten wir zwei Filter $\rm A$ und $\rm B$ mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit der Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$. |
| − | *Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils $1$ ergeben. | + | *Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils $1$ ergeben. |
| Zeile 18: | Zeile 18: | ||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Systembeschreibung im Zeitbereich]] | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Systembeschreibung im Zeitbereich]] | ||
| − | * Informationen zur Faltung finden Sie im Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]] | + | * Informationen zur Faltung finden Sie im Kapitel [[Signaldarstellung/Faltungssatz_und_Faltungsoperation|Faltungssatz und Faltungsoperation]] im Buch „Signaldarstellung”. |
| − | *Wir verweisen auch auf das interaktive Applet [[Applets: | + | *Wir verweisen Sie auch auf das interaktive Applet [[Applets:Zur_Verdeutlichung_der_grafischen_Faltung|Zur Verdeutlichung der graphischen Faltung]]. |
| Zeile 27: | Zeile 27: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Berechnen Sie das Ausgangssignal $y_{\rm A}(t)$ von Filter $\rm A$, insbesondere die Werte bei $t = 0$ und $t = T$. | + | {Berechnen Sie das Ausgangssignal $y_{\rm A}(t)$ von Filter $\rm A$, insbesondere die Werte bei $t = 0$ und $t = T$. |
|type="{}"} | |type="{}"} | ||
$y_{\rm A}(t = 0) \ =\ $ { 1 3% } $\rm V$ | $y_{\rm A}(t = 0) \ =\ $ { 1 3% } $\rm V$ | ||
| Zeile 33: | Zeile 33: | ||
| − | {Geben Sie die Betragsfunktion $|H_{\rm A}(f)|$ an. Welcher Wert ergibt sich bei der Frequenz $f = f_0$? <br>Interpretieren Sie das Ergebnis der Teilaufgabe '''(1)'''. | + | {Geben Sie die Betragsfunktion $|H_{\rm A}(f)|$ an. Welcher Wert ergibt sich bei der Frequenz $f = f_0$? <br>Interpretieren Sie das Ergebnis der Teilaufgabe '''(1)'''. |
|type="{}"} | |type="{}"} | ||
$|H_{\rm A}(f = f_0)| \ =\ $ { 0. } | $|H_{\rm A}(f = f_0)| \ =\ $ { 0. } | ||
| − | {Berechnen Sie das Ausgangssignal $y_{\rm B}(t)$ von Filter $\rm B$, insbesondere die Werte bei $t = 0$ und $t = T$. | + | {Berechnen Sie das Ausgangssignal $y_{\rm B}(t)$ von Filter $\rm B$, insbesondere die Werte bei $t = 0$ und $t = T$. |
|type="{}"} | |type="{}"} | ||
$y_{\rm B}(t = 0) \ =\ $ { 0.8 3% } $\rm V$ | $y_{\rm B}(t = 0) \ =\ $ { 0.8 3% } $\rm V$ | ||
| Zeile 44: | Zeile 44: | ||
| − | {Wie lautet die Betragsfunktion $|H_{\rm B}(f)|$, insbesondere bei den Frequenzen $f = f_0$ und $f = 3 · f_0$? <br>Interpretieren Sie damit das Ergebnis | + | {Wie lautet die Betragsfunktion $|H_{\rm B}(f)|$, insbesondere bei den Frequenzen $f = f_0$ und $f = 3 · f_0$? <br>Interpretieren Sie damit das Ergebnis der Teilaufgabe '''(3)'''. |
|type="{}"} | |type="{}"} | ||
$|H_{\rm B}(f = f_0)| \ =\ $ { 0.127 5% } | $|H_{\rm B}(f = f_0)| \ =\ $ { 0.127 5% } | ||
| Zeile 53: | Zeile 53: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen $x(t)$ und $h_{\rm A}(t)$: | + | '''(1)''' Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen $x(t)$ und $h_{\rm A}(t)$: |
:$$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | :$$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$ | ||
| − | Aufgrund der Rechteckfunktion und der Dauer $6T$ kann hierfür auch geschrieben werden: | + | *Aufgrund der Rechteckfunktion und der Dauer $6T$ kann hierfür auch geschrieben werden: |
:$$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ | :$$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | Man erkennt, dass diese Gleichung für alle $t$ das gleiche Ergebnis $y_{\rm A}(t) \rm \underline{\: = 1V}$ liefert. | + | *Man erkennt, dass diese Gleichung für alle $t$ das gleiche Ergebnis $y_{\rm A}(t) \rm \underline{\: = 1V}$ liefert. |
| − | '''(2)''' Der Betragsfrequenzgang lautet $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ Dieser weist Nullstellen im Abstand $1/(6T)$ auf. | + | |
| − | *Somit liegen auch bei $f_0$, $3f_0$, $5f_0$ usw. jeweils Nullstellen vor. | + | '''(2)''' Der Betragsfrequenzgang lautet $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ Dieser weist Nullstellen im Abstand $1/(6T)$ auf. |
| − | *Insbesondere gilt auch $|H_{\rm A}(f = f_0)| \underline{\: = 0}$. | + | *Somit liegen auch bei $f_0$, $3f_0$, $5f_0$ usw. jeweils Nullstellen vor. |
| − | *Vom Spektrum $X(f)$ bleibt somit nur der Gleichanteil $1 \ \rm V$ unverändert erhalten. | + | *Insbesondere gilt auch $|H_{\rm A}(f = f_0)| \underline{\: = 0}$. |
| − | *Dagegen sind alle anderen Spektrallinien in $Y_{\rm A}(f)$ nicht mehr enthalten. | + | *Vom Spektrum $X(f)$ bleibt somit nur der Gleichanteil $1 \hspace{0.05cm} \rm V$ unverändert erhalten. |
| + | *Dagegen sind alle anderen Spektrallinien in $Y_{\rm A}(f)$ nicht mehr enthalten. | ||
[[Datei:P_ID836__LZI_Z_1_4_c.png | Grafische Verdeutlichung der Faltungsoperation| rechts|frame]] | [[Datei:P_ID836__LZI_Z_1_4_c.png | Grafische Verdeutlichung der Faltungsoperation| rechts|frame]] | ||
| − | '''(3)''' Analog zur Teilaufgabe (1) kann hier für das Ausgangssignal | + | '''(3)''' Analog zur Teilaufgabe '''(1)''' kann man hier für das Ausgangssignal schreiben: |
:$$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ | :$$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | Es ergibt sich | + | *Es ergibt sich ein um den Mittelwert $1 \ \rm V$ schwankender dreieckförmiger Verlauf ⇒ siehe untere Grafik. |
| − | *Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt | + | *Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt für $t = 0, t = 2T,$ usw.: |
:$$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$ | :$$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$ | ||
| − | * | + | *Bei $t = T,\ 3T, \ 5T, $ usw. sind jeweils drei Rechtecke und zwei Lücken zu berücksichtigen: Man erhält: |
:$$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$ | :$$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$ | ||
| − | '''(4)''' Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen $f = f_0 = 1/(2T)$ und $f = 3f_0$: | + | |
| + | '''(4)''' Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen $f = f_0 = 1/(2T)$ und $f = 3f_0$: | ||
:$$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$ | :$$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$ | ||
Interpretation: | Interpretation: | ||
| − | *Die Spektralanteile des Rechtecksignals bei $f_0, 3f_0,$ usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird. Der Gleichanteil bleibt auch hier unverändert. | + | *Die Spektralanteile des Rechtecksignals bei $f_0, 3f_0,$ usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird. Der Gleichanteil $(1 \hspace{0.05cm} \rm V)$ bleibt auch hier unverändert. |
| − | *Beide Filter liefern also den Mittelwert des Eingangssignals. Beim vorliegenden Signal $x(t)$ ist für die Bestimmung des Mittelwertes das Filter $\rm A$ besser geeignet als das Filter $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer $T_0 = 2T$ ist. | + | *Beide Filter liefern also den Mittelwert des Eingangssignals. Beim vorliegenden Signal $x(t)$ ist für die Bestimmung des Mittelwertes das Filter $\rm A$ besser geeignet als das Filter $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer $T_0 = 2T$ ist. |
| − | *Ist diese Bedingung – wie beim Filter $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal. | + | *Ist diese Bedingung – wie beim Filter $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 18. Oktober 2019, 13:58 Uhr
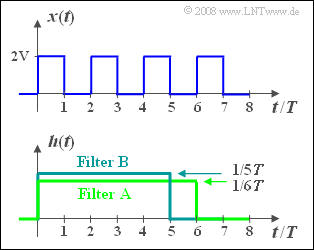
Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist.
- Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, das heißt bei $3f_0$, $5f_0,$ usw. Zusätzlich gibt es einen Gleichanteil.
- Dazu betrachten wir zwei Filter $\rm A$ und $\rm B$ mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit der Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$.
- Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils $1$ ergeben.
Hinweise:
- Die Aufgabe gehört zum Kapitel Systembeschreibung im Zeitbereich
- Informationen zur Faltung finden Sie im Kapitel Faltungssatz und Faltungsoperation im Buch „Signaldarstellung”.
- Wir verweisen Sie auch auf das interaktive Applet Zur Verdeutlichung der graphischen Faltung.
Fragebogen
Musterlösung
(1) Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen $x(t)$ und $h_{\rm A}(t)$:
- $$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$
- Aufgrund der Rechteckfunktion und der Dauer $6T$ kann hierfür auch geschrieben werden:
- $$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$
- Man erkennt, dass diese Gleichung für alle $t$ das gleiche Ergebnis $y_{\rm A}(t) \rm \underline{\: = 1V}$ liefert.
(2) Der Betragsfrequenzgang lautet $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ Dieser weist Nullstellen im Abstand $1/(6T)$ auf.
- Somit liegen auch bei $f_0$, $3f_0$, $5f_0$ usw. jeweils Nullstellen vor.
- Insbesondere gilt auch $|H_{\rm A}(f = f_0)| \underline{\: = 0}$.
- Vom Spektrum $X(f)$ bleibt somit nur der Gleichanteil $1 \hspace{0.05cm} \rm V$ unverändert erhalten.
- Dagegen sind alle anderen Spektrallinien in $Y_{\rm A}(f)$ nicht mehr enthalten.
(3) Analog zur Teilaufgabe (1) kann man hier für das Ausgangssignal schreiben:
- $$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$
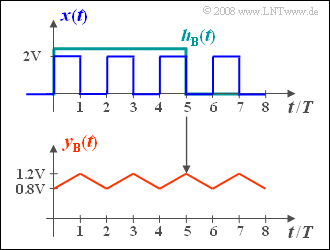
- Es ergibt sich ein um den Mittelwert $1 \ \rm V$ schwankender dreieckförmiger Verlauf ⇒ siehe untere Grafik.
- Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt für $t = 0, t = 2T,$ usw.:
- $$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$
- Bei $t = T,\ 3T, \ 5T, $ usw. sind jeweils drei Rechtecke und zwei Lücken zu berücksichtigen: Man erhält:
- $$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$
(4) Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen $f = f_0 = 1/(2T)$ und $f = 3f_0$:
- $$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$
Interpretation:
- Die Spektralanteile des Rechtecksignals bei $f_0, 3f_0,$ usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird. Der Gleichanteil $(1 \hspace{0.05cm} \rm V)$ bleibt auch hier unverändert.
- Beide Filter liefern also den Mittelwert des Eingangssignals. Beim vorliegenden Signal $x(t)$ ist für die Bestimmung des Mittelwertes das Filter $\rm A$ besser geeignet als das Filter $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer $T_0 = 2T$ ist.
- Ist diese Bedingung – wie beim Filter $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal.