Aufgaben:Aufgabe 1.8: Variable Flankensteilheit: Unterschied zwischen den Versionen
Javier (Diskussion | Beiträge) |
|||
| (4 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/ | + | {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Einige systemtheoretische Tiefpassfunktionen}} |
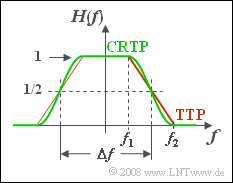
[[Datei:P_ID867__LZI_A_1_8.png|right|frame|Trapez–Tiefpass (rot) und Cosinus–Rolloff–Tiefpass (grün)]] | [[Datei:P_ID867__LZI_A_1_8.png|right|frame|Trapez–Tiefpass (rot) und Cosinus–Rolloff–Tiefpass (grün)]] | ||
| − | Zwei Tiefpässe mit variabler Flankensteilheit werden miteinander verglichen. Für Frequenzen $|f| ≤ f_1$ gilt in beiden Fällen $H(f) = 1$. Dagegen werden alle Frequenzen $|f| ≥ f_2$ vollständig unterdrückt. | + | Zwei Tiefpässe mit variabler Flankensteilheit werden miteinander verglichen. Für Frequenzen $|f| ≤ f_1$ gilt in beiden Fällen $H(f) = 1$. Dagegen werden alle Frequenzen $|f| ≥ f_2$ vollständig unterdrückt. |
Im Bereich $f_1 ≤ |f| ≤ f_2$ sind die Frequenzgänge durch folgende Gleichungen festgelegt: | Im Bereich $f_1 ≤ |f| ≤ f_2$ sind die Frequenzgänge durch folgende Gleichungen festgelegt: | ||
| Zeile 23: | Zeile 23: | ||
\frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta | \frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta | ||
t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$ | t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$ | ||
| + | |||
| + | |||
| + | |||
| Zeile 30: | Zeile 33: | ||
''Hinweise:'' | ''Hinweise:'' | ||
*Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen|Einige systemtheoretische Tiefpassfunktionen]]. | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen|Einige systemtheoretische Tiefpassfunktionen]]. | ||
| − | *Bezug genommen wird insbesondere auf die Seiten | + | *Bezug genommen wird insbesondere auf die Seiten [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Trapez.E2.80.93Tiefpass|Trapez–Tiefpass]] sowie [[Lineare_zeitinvariante_Systeme/Einige_systemtheoretische_Tiefpassfunktionen#Cosinus-Rolloff-Tiefpass|Cosinus–Rolloff–Tiefpass]]. |
| − | |||
| − | |||
*Sie können Ihre Ergebnisse mit dem interaktiven Applet [[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang und Impulsantwort]] überprüfen. | *Sie können Ihre Ergebnisse mit dem interaktiven Applet [[Applets:Frequenzgang_und_Impulsantwort|Frequenzgang und Impulsantwort]] überprüfen. | ||
| Zeile 40: | Zeile 41: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet die Gleichung für die äquivalente Bandbreite $Δf$? Es gilt | + | {Wie lautet die Gleichung für die äquivalente Bandbreite $Δf$? Es gilt |
|type="[]"} | |type="[]"} | ||
- $Δf = f_2 - f_1$, | - $Δf = f_2 - f_1$, | ||
| Zeile 55: | Zeile 56: | ||
{Welche Aussagen sind für die Impulsantwort des Trapez–Tiefpasses zutreffend, wenn $r = 0.2$ vorausgesetzt wird? | {Welche Aussagen sind für die Impulsantwort des Trapez–Tiefpasses zutreffend, wenn $r = 0.2$ vorausgesetzt wird? | ||
|type="[]"} | |type="[]"} | ||
| − | + $h(t)$ besitzt Nullstellen bei $ | + | + $h(t)$ besitzt Nullstellen bei $±\hspace{0.03cm}n · Δt \ (n = 1, 2, \text{...})$. |
- $h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten. | - $h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten. | ||
- Mit $r = 0$ würde $h(t)$ schneller abklingen. | - Mit $r = 0$ würde $h(t)$ schneller abklingen. | ||
| Zeile 63: | Zeile 64: | ||
{Welche Aussagen treffen für die Impulantwort des Cosinus–Rolloff–Tiefpasses zu, wenn $r = 0.2$ vorausgesetzt wird? | {Welche Aussagen treffen für die Impulantwort des Cosinus–Rolloff–Tiefpasses zu, wenn $r = 0.2$ vorausgesetzt wird? | ||
|type="[]"} | |type="[]"} | ||
| − | + $h(t)$ besitzt Nullstellen bei $ | + | + $h(t)$ besitzt Nullstellen bei $±\hspace{0.03cm}n · Δt \ (n = 1, 2, \text{...})$. |
+ $h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten. | + $h(t)$ besitzt zusätzliche Nullstellen zu anderen Zeiten. | ||
- Mit $r = 0$ würde $h(t)$ schneller abklingen. | - Mit $r = 0$ würde $h(t)$ schneller abklingen. | ||
| Zeile 74: | Zeile 75: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| − | *Bei beiden Tiefpässen ist das Integral über $H(f)$ gleich $f_1 + f_2$. Wegen $H(f = 0 = 1)$ stimmt somit der <u>Lösungsvorschlag 2</u>: $\Delta f = f_1 + f_2.$ | + | *Bei beiden Tiefpässen ist das Integral über $H(f)$ gleich $f_1 + f_2$. |
| + | *Wegen $H(f = 0 = 1)$ stimmt somit der <u>Lösungsvorschlag 2</u>: $\Delta f = f_1 + f_2.$ | ||
| + | |||
| − | '''(2)''' Setzt man die unter '''(1)''' gefundene Beziehung in die Definitionsgleichung des Rolloff–Faktors ein, so erhält man | + | '''(2)''' Setzt man die unter '''(1)''' gefundene Beziehung in die Definitionsgleichung des Rolloff–Faktors ein, so erhält man |
:$${f_2 - f_1} = r \cdot \Delta f = {2\,\rm | :$${f_2 - f_1} = r \cdot \Delta f = {2\,\rm | ||
kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm | kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm | ||
kHz}.$$ | kHz}.$$ | ||
| − | Durch Addition bzw. Subtraktion beider Gleichungen ergeben sich die so genannten „Eckfrequenzen” zu $f_1 \underline{= 4 \ \rm kHz}$ | + | *Durch Addition bzw. Subtraktion beider Gleichungen ergeben sich die so genannten „Eckfrequenzen” zu |
| + | :$$f_1 \underline{= 4 \ \rm kHz},$$ | ||
| + | :$$f_2 \underline{= 6 \ \rm kHz}.$$ | ||
| Zeile 90: | Zeile 95: | ||
*Da diese exakt mit den Nullstellen der ersten $\rm si$–Funktion zusammenfallen, gibt es keine zusätzlichen Nullstellen. | *Da diese exakt mit den Nullstellen der ersten $\rm si$–Funktion zusammenfallen, gibt es keine zusätzlichen Nullstellen. | ||
*Der Sonderfall $r = 0$ entspricht dem idealen rechteckförmigen Tiefpass mit $\rm si$–förmiger Impulsantwort. Diese klingt extrem langsam ab. | *Der Sonderfall $r = 0$ entspricht dem idealen rechteckförmigen Tiefpass mit $\rm si$–förmiger Impulsantwort. Diese klingt extrem langsam ab. | ||
| − | *Die $\rm si^2$–förmige Impulsantwort des Dreiecktiefpasses (Sonderfall für $r = 1$ | + | *Die $\rm si^2$–förmige Impulsantwort des Dreiecktiefpasses $($Sonderfall für $r = 1)$ fällt asymptotisch mit $1/t^2$, also schneller als mit $r = 0.2$. |
| Zeile 104: | Zeile 109: | ||
*Die weiteren Nullstellen bei $7.5, 12.5,\text{...} $ bleiben dagegen bestehen. | *Die weiteren Nullstellen bei $7.5, 12.5,\text{...} $ bleiben dagegen bestehen. | ||
*Auch hier führt $r = 0$ zum Rechtecktiefpass und damit zur $\rm si$–förmigen Impulsantwort. | *Auch hier führt $r = 0$ zum Rechtecktiefpass und damit zur $\rm si$–förmigen Impulsantwort. | ||
| − | *Dagegen klingt die Impulsantwort des Cosinus–Quadrat–Tiefpasses (Sonderfall für $r = 1$ | + | *Dagegen klingt die Impulsantwort des Cosinus–Quadrat–Tiefpasses $($Sonderfall für $r = 1)$ extrem schnell ab. |
| − | *Dieser wird in der [[Aufgaben:1.8Z_Cosinus-Quadrat-Tiefpass|Aufgabe 1.8Z]] eingehend untersucht. | + | *Dieser wird in der [[Aufgaben:1.8Z_Cosinus-Quadrat-Tiefpass|Aufgabe 1.8Z]] eingehend untersucht. |
| Zeile 112: | Zeile 117: | ||
| − | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^1.3 | + | [[Category:Aufgaben zu Lineare zeitinvariante Systeme|^1.3 Systemtheoretische Tiefpassfunktionen^]] |
Aktuelle Version vom 13. September 2021, 10:28 Uhr
Zwei Tiefpässe mit variabler Flankensteilheit werden miteinander verglichen. Für Frequenzen $|f| ≤ f_1$ gilt in beiden Fällen $H(f) = 1$. Dagegen werden alle Frequenzen $|f| ≥ f_2$ vollständig unterdrückt.
Im Bereich $f_1 ≤ |f| ≤ f_2$ sind die Frequenzgänge durch folgende Gleichungen festgelegt:
- Trapeztiefpass (TTP):
- $$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$
- Cosinus–Rolloff–Tiefpass (CRTP):
- $$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$
Alternative Systemparameter sind für beide Tiefpässe
- die über das flächengleiche Rechteck definierte äquivalente Bandbreite $Δf$, sowie
- der Rolloff–Faktor (im Frequenzbereich):
- $$r=\frac{f_2 - f_1}{f_2 + f_1} .$$
In der gesamten Aufgabe gelte $Δf = 10 \ \rm kHz$ und $r = 0.2$.
Die Impulsantworten lauten mit der äquivalenten Impulsdauer $Δt = 1/Δf = 0.1 \ \rm ms$:
- $$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$
- $$h_{\rm CRTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige systemtheoretische Tiefpassfunktionen.
- Bezug genommen wird insbesondere auf die Seiten Trapez–Tiefpass sowie Cosinus–Rolloff–Tiefpass.
- Sie können Ihre Ergebnisse mit dem interaktiven Applet Frequenzgang und Impulsantwort überprüfen.
Fragebogen
Musterlösung
- Bei beiden Tiefpässen ist das Integral über $H(f)$ gleich $f_1 + f_2$.
- Wegen $H(f = 0 = 1)$ stimmt somit der Lösungsvorschlag 2: $\Delta f = f_1 + f_2.$
(2) Setzt man die unter (1) gefundene Beziehung in die Definitionsgleichung des Rolloff–Faktors ein, so erhält man
- $${f_2 - f_1} = r \cdot \Delta f = {2\,\rm kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm kHz}.$$
- Durch Addition bzw. Subtraktion beider Gleichungen ergeben sich die so genannten „Eckfrequenzen” zu
- $$f_1 \underline{= 4 \ \rm kHz},$$
- $$f_2 \underline{= 6 \ \rm kHz}.$$
(3) Richtig sind die Lösungsvorschläge 1 und 4:
- Die erste $\rm si$–Funktion von $h_{\rm TTP}(t)$ führt zu Nullstellen im Abstand $\Delta t$ (siehe auch Gleichung auf der Angabenseite).
- Die zweite $\rm si$–Funktion bewirkt Nullstellen bei Vielfachen von $5 · \Delta t$.
- Da diese exakt mit den Nullstellen der ersten $\rm si$–Funktion zusammenfallen, gibt es keine zusätzlichen Nullstellen.
- Der Sonderfall $r = 0$ entspricht dem idealen rechteckförmigen Tiefpass mit $\rm si$–förmiger Impulsantwort. Diese klingt extrem langsam ab.
- Die $\rm si^2$–förmige Impulsantwort des Dreiecktiefpasses $($Sonderfall für $r = 1)$ fällt asymptotisch mit $1/t^2$, also schneller als mit $r = 0.2$.
(4) Richtig sind hier die Vorschläge 1, 2 und 4:
- Die Impulsantwort $h_{\rm CRTP}(t)$ des Cosinus-Rolloff-Tiefpasses hat aufgrund der si–Funktion ebenfalls Nullstellen im Abstand $\Delta t$.
- Die Cosinusfunktion hat Nullstellen zu folgenden Zeitpunkten:
- $${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm 0.5, \pm 1.5, \pm 2.5, \text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, ... $$
- $$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, \text{...}. $$
- Die Nullstelle des Zählers bei $t / \Delta t = 2.5$ wird allerdings durch den ebenfalls verschwindenden Nenner zunichte gemacht.
- Die weiteren Nullstellen bei $7.5, 12.5,\text{...} $ bleiben dagegen bestehen.
- Auch hier führt $r = 0$ zum Rechtecktiefpass und damit zur $\rm si$–förmigen Impulsantwort.
- Dagegen klingt die Impulsantwort des Cosinus–Quadrat–Tiefpasses $($Sonderfall für $r = 1)$ extrem schnell ab.
- Dieser wird in der Aufgabe 1.8Z eingehend untersucht.