Aufgaben:Aufgabe 2.2: Verzerrungsleistung: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID883__LZI_A_2_2.png|right|frame|Eingangssignal und Ausgangssignale]] | [[Datei:P_ID883__LZI_A_2_2.png|right|frame|Eingangssignal und Ausgangssignale]] | ||
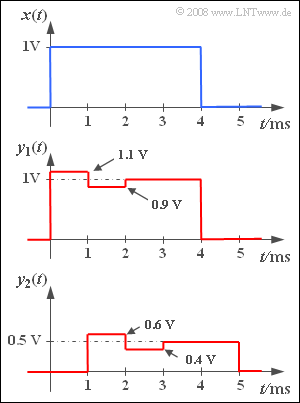
| − | Am Eingang eines Nachrichtensystems $S_1$ wird ein Rechteckimpuls $x(t)$ mit der Amplitude $1 \hspace{0.08cm} \rm V$ und der Dauer $4 \hspace{0.08cm} \rm ms$ angelegt. Am Systemausgang wird dann der Impuls $y_1(t)$ gemessen, dessen Signalparameter der mittleren Skizze entnommen werden können. | + | Am Eingang eines Nachrichtensystems $S_1$ wird ein Rechteckimpuls $x(t)$ mit der Amplitude $1 \hspace{0.08cm} \rm V$ und der Dauer $4 \hspace{0.08cm} \rm ms$ angelegt. Am Systemausgang wird dann der Impuls $y_1(t)$ gemessen, dessen Signalparameter der mittleren Skizze entnommen werden können. |
| − | Am Ausgang eines anderen Systems $S_2$ stellt sich bei gleichem Eingangssignal $x(t)$ das in dem unteren Bild dargestellte Signal $y_2(t)$ ein. | + | Am Ausgang eines anderen Systems $S_2$ stellt sich bei gleichem Eingangssignal $x(t)$ das in dem unteren Bild dargestellte Signal $y_2(t)$ ein. |
Für das in dieser Aufgabe verwendete Fehlersignal gelte folgende Definition: | Für das in dieser Aufgabe verwendete Fehlersignal gelte folgende Definition: | ||
| Zeile 17: | Zeile 17: | ||
Das Integrationsintervall ist jeweils geeignet zu wählen: | Das Integrationsintervall ist jeweils geeignet zu wählen: | ||
| − | *Benutzen Sie für $y_1(t)$ den Bereich von $0$ ... $4 \hspace{0.08cm} \rm ms$ und für $y_2(t)$ das Intervall $1 \hspace{0.08cm} {\rm ms}$ ... $5 \hspace{0.08cm} \rm ms$. | + | *Benutzen Sie für $y_1(t)$ den Bereich von $0$ ... $4 \hspace{0.08cm} \rm ms$ und für $y_2(t)$ das Intervall $1 \hspace{0.08cm} {\rm ms}$ ... $5 \hspace{0.08cm} \rm ms$. |
*Damit beträgt in beiden Fällen die Messdauer $T_{\rm M} = 4 \hspace{0.08cm} \rm ms$. | *Damit beträgt in beiden Fällen die Messdauer $T_{\rm M} = 4 \hspace{0.08cm} \rm ms$. | ||
*Es ist offensichtlich, dass bezüglich $y_1(t)$ die Parameter $\alpha = 1$ und $\tau = 0$ jeweils zur minimalen Verzerrungsleistung führen. | *Es ist offensichtlich, dass bezüglich $y_1(t)$ die Parameter $\alpha = 1$ und $\tau = 0$ jeweils zur minimalen Verzerrungsleistung führen. | ||
| Zeile 26: | Zeile 26: | ||
Hierbei bezeichnet | Hierbei bezeichnet | ||
| − | *$P_x$ die Leistung des Signals $x(t)$, und | + | *$P_x$ die Leistung des Signals $x(t)$, und |
| − | *$\alpha^2 \cdot P_x$ die Leistung von $y(t) = \alpha \cdot x(t - \tau)$, die sich bei Abwesenheit von Verzerrungen ergeben würde. | + | *$\alpha^2 \cdot P_x$ die Leistung von $y(t) = \alpha \cdot x(t - \tau)$, die sich bei Abwesenheit von Verzerrungen ergeben würde. |
| − | Meist – so auch in dieser Aufgabe – wird dieses S/N-Verhältnis $\rho_{\rm V}$ logarithmisch in $\rm dB$ angegeben. | + | Meist – so auch in dieser Aufgabe – wird dieses S/N-Verhältnis $\rho_{\rm V}$ logarithmisch in $\rm dB$ angegeben. |
| Zeile 48: | Zeile 48: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ermitteln Sie die Verzerrungsleistung des Systems $S_1$. | + | {Ermitteln Sie die Verzerrungsleistung des Systems $S_1$. |
|type="{}"} | |type="{}"} | ||
$P_{\rm V1} \ = \ $ { 5 3% } $\ \cdot 10^{-3} \ {\rm V}^2$ | $P_{\rm V1} \ = \ $ { 5 3% } $\ \cdot 10^{-3} \ {\rm V}^2$ | ||
| − | {Berechnen Sie das Signal–zu–Verzerrungs–Leistungsverhältnis für System $S_1$. | + | {Berechnen Sie das Signal–zu–Verzerrungs–Leistungsverhältnis für System $S_1$. |
|type="{}"} | |type="{}"} | ||
$10 \cdot {\rm lg} \ \rho_\text{V1} \ = \ $ { 23.01 3% } $\ \rm dB$ | $10 \cdot {\rm lg} \ \rho_\text{V1} \ = \ $ { 23.01 3% } $\ \rm dB$ | ||
| − | {Welche Parameter $\alpha$ und $\tau$ sollten zur Berechnung der Verzerrungsleistung des Systems $S_2$ herangezogen werden? <br>Begründen Sie Ihr Ergebnis. | + | {Welche Parameter $\alpha$ und $\tau$ sollten zur Berechnung der Verzerrungsleistung des Systems $S_2$ herangezogen werden? <br>Begründen Sie Ihr Ergebnis. |
|type="{}"} | |type="{}"} | ||
$\alpha \ = \ $ { 0.5 3% } | $\alpha \ = \ $ { 0.5 3% } | ||
| Zeile 64: | Zeile 64: | ||
| − | {Ermitteln Sie die Verzerrungsleistung des Systems $S_2$. | + | {Ermitteln Sie die Verzerrungsleistung des Systems $S_2$. |
|type="{}"} | |type="{}"} | ||
$P_{\rm V2} \ = \ $ { 5 3% } $\ \cdot 10^{-3} \ {\rm V}^2$ | $P_{\rm V2} \ = \ $ { 5 3% } $\ \cdot 10^{-3} \ {\rm V}^2$ | ||
| − | {Berechnen Sie das Signal–zu–Verzerrungs–Leistungsverhältnis für das System $S_2$. <br>Interpretieren Sie die unterschiedlichen Ergebnisse. | + | {Berechnen Sie das Signal–zu–Verzerrungs–Leistungsverhältnis für das System $S_2$. <br>Interpretieren Sie die unterschiedlichen Ergebnisse. |
|type="{}"} | |type="{}"} | ||
$10 \cdot {\rm lg} \ \rho_\text{V2} \ = \ $ { 16.99 3% } $\ \rm dB$ | $10 \cdot {\rm lg} \ \rho_\text{V2} \ = \ $ { 16.99 3% } $\ \rm dB$ | ||
| Zeile 80: | Zeile 80: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
[[Datei:P_ID915__LZI_A_2_2_a.png|right|frame|Resultierende Fehlersignale]] | [[Datei:P_ID915__LZI_A_2_2_a.png|right|frame|Resultierende Fehlersignale]] | ||
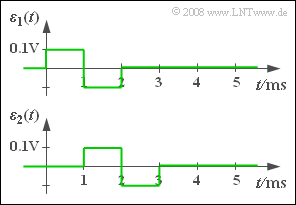
| − | '''(1)''' Mit den gegebenen Parametern $\alpha = 1$ und $\tau= 0$ erhält man das in der Grafik dargestellte Fehlersignal $\ | + | '''(1)''' Mit den gegebenen Parametern $\alpha = 1$ und $\tau= 0$ erhält man das in der Grafik dargestellte Fehlersignal $\varepsilon_1(t)$. Die Verzerrungsleistung ist somit gleich: |
| − | :$$P_{\rm V1} = \frac{ {1 \, \rm ms}}{4 \, \rm ms} \cdot \ | + | :$$P_{\rm V1} = \frac{ {1 \, \rm ms}}{4 \, \rm ms} \cdot \big[ ({0.1 \, \rm V})^2 + |
| − | ({-0.1 \, \rm V})^2\ | + | ({-0.1 \, \rm V})^2\big]\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm V1} \hspace{0.15cm}\underline{ = 5 \cdot 10^{-3} \, \rm V^2}. $$ |
| + | |||
| Zeile 88: | Zeile 89: | ||
:$$P_{x} = \frac{1}{4 \, \rm ms} \cdot ({1 \, \rm V})^2 \cdot {4 \, \rm ms}\hspace{0.15cm}{ = {1 \, \rm V^2}}.$$ | :$$P_{x} = \frac{1}{4 \, \rm ms} \cdot ({1 \, \rm V})^2 \cdot {4 \, \rm ms}\hspace{0.15cm}{ = {1 \, \rm V^2}}.$$ | ||
| − | Mit dem Ergebnis aus (1) erhält man somit für das Signal–zu–Verzerrungs–Leistungsverhältnis: | + | *Mit dem Ergebnis aus '''(1)''' erhält man somit für das Signal–zu–Verzerrungs–Leistungsverhältnis: |
$$\rho_{\rm V1} = \frac{ P_{x}}{P_{\rm V1}}= \frac{ {1 \, \rm | $$\rho_{\rm V1} = \frac{ P_{x}}{P_{\rm V1}}= \frac{ {1 \, \rm | ||
V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 200\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 200\hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
| Zeile 94: | Zeile 95: | ||
| − | |||
| − | Wenn jemand diese Werte nicht sofort aus der Grafik erkennt, so müsste er für sehr (unendlich) viele $\alpha$– und $\tau$–Werte zunächst das Fehlersignal | + | '''(3)''' Die Skizze auf dem Angabenblatt macht deutlich, dass sich auch ohne die auftretenden Verzerrungen – sondern allein durch Dämpfung und Laufzeit das Signal $y(t)$ von $x(t)$ – deutlich unterscheiden würde. |
| + | *Es würde sich $y(t) = 0.5 \cdot x(t-1\ {\rm ms}) $ ergeben. | ||
| + | |||
| + | *Wenn jemand diese Werte nicht sofort aus der Grafik erkennt, so müsste er für sehr (unendlich) viele $\alpha$– und $\tau$–Werte zunächst das Fehlersignal | ||
:$$\varepsilon_2(t) = y_2(t) - \alpha \cdot x(t - \tau)$$ | :$$\varepsilon_2(t) = y_2(t) - \alpha \cdot x(t - \tau)$$ | ||
| − | und anschließend den mittleren quadratischen Fehler ermitteln, wobei das Integrationsintervall jeweils an $\tau$ anzupassen ist. Auch dann würde man das kleinstmögliche Ergebnis für $\alpha \; \underline{= 0.5}$ und $\tau \; \underline{= 1 \ \rm ms}$ erhalten. Für diese Optimierung von $\alpha$ und $\tau$ sollte man sich allerdings schon ein Computerprogramm gönnen. | + | :und anschließend den mittleren quadratischen Fehler ermitteln, wobei das Integrationsintervall jeweils an $\tau$ anzupassen ist. |
| + | *Auch dann würde man das kleinstmögliche Ergebnis für $\alpha \; \underline{= 0.5}$ und $\tau \; \underline{= 1 \ \rm ms}$ erhalten. Für diese Optimierung von $\alpha$ und $\tau$ sollte man sich allerdings schon ein Computerprogramm gönnen. | ||
| + | |||
| − | '''(4)''' Die obige Skizze zeigt, dass $\varepsilon_2(t)$ bis auf eine Verschiebung um $1 \ \rm ms$ gleich dem Fehlersignal $\varepsilon_1(t)$ ist. Mit dem Integrationsintervall $1 \ {\rm ms}$ ... $5 \ {\rm ms}$ ergibt sich somit auch die gleiche Verzerrungsleistung: | + | '''(4)''' Die obige Skizze zeigt, dass $\varepsilon_2(t)$ bis auf eine Verschiebung um $1 \ \rm ms$ gleich dem Fehlersignal $\varepsilon_1(t)$ ist. Mit dem Integrationsintervall $1 \ {\rm ms}$ ... $5 \ {\rm ms}$ ergibt sich somit auch die gleiche Verzerrungsleistung: |
:$$P_{\rm V2} = P_{\rm V1} \hspace{0.15cm}\underline{ = 5 \cdot 10^{-3} \, \rm V^2}.$$ | :$$P_{\rm V2} = P_{\rm V1} \hspace{0.15cm}\underline{ = 5 \cdot 10^{-3} \, \rm V^2}.$$ | ||
| + | |||
| Zeile 111: | Zeile 117: | ||
10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2} \hspace{0.15cm}\underline{= {16.99 \, \rm dB}}.$$ | 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2} \hspace{0.15cm}\underline{= {16.99 \, \rm dB}}.$$ | ||
| − | Trotz gleicher Verzerrungsleistung ist $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2}$ gegenüber $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V1}$ um etwa $6 \ \rm dB$ geringer. Das Signal $y_2(t)$ ist also hinsichtlich des SNR deutlich ungünstiger als $y_1(t)$. | + | *Trotz gleicher Verzerrungsleistung ist $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2}$ gegenüber $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V1}$ um etwa $6 \ \rm dB$ geringer. |
| + | *Das Signal $y_2(t)$ ist also hinsichtlich des SNR deutlich ungünstiger als $y_1(t)$. | ||
| + | * Es ist berücksichtigt, dass nun wegen $\alpha = 0.5$ die Leistung des Ausgangssignals nur noch ein Viertel der Eingangsleistung beträgt. | ||
| + | *Würde man diese Dämpfung am Ausgang durch eine Verstärkung um $1/\alpha$ kompensieren, so würde zwar die Verzerrungsleistung um $\alpha^2$ größer. | ||
| − | + | *Das Signal-zu-Verzerrungs-Leistungsverhältnis $\rho_{\rm V2}$ bliebe jedoch erhalten, weil auch das „Nutzsignal” um den gleichen Betrag angehoben wird. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 28. Oktober 2019, 09:20 Uhr
Am Eingang eines Nachrichtensystems $S_1$ wird ein Rechteckimpuls $x(t)$ mit der Amplitude $1 \hspace{0.08cm} \rm V$ und der Dauer $4 \hspace{0.08cm} \rm ms$ angelegt. Am Systemausgang wird dann der Impuls $y_1(t)$ gemessen, dessen Signalparameter der mittleren Skizze entnommen werden können.
Am Ausgang eines anderen Systems $S_2$ stellt sich bei gleichem Eingangssignal $x(t)$ das in dem unteren Bild dargestellte Signal $y_2(t)$ ein.
Für das in dieser Aufgabe verwendete Fehlersignal gelte folgende Definition:
- $$\varepsilon(t) = y(t) - \alpha \cdot x(t - \tau) .$$
Die Parameter $\alpha$ und $\tau$ sind so zu bestimmen, dass die Verzerrungsleistung (der mittlere quadratische Fehler) minimal ist. Für diese gilt:
- $$P_{\rm V} = \overline{\varepsilon^2(t)} = \frac{1}{T_{\rm M}} \cdot \int\limits_{ ( T_{\rm M})} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t$$
Bei diesen Definitionen ist bereits berücksichtigt, dass eine frequenzunabhängige Dämpfung ebenso wie eine für alle Frequenzen konstante Laufzeit nicht zur Verzerrung beiträgt.
Das Integrationsintervall ist jeweils geeignet zu wählen:
- Benutzen Sie für $y_1(t)$ den Bereich von $0$ ... $4 \hspace{0.08cm} \rm ms$ und für $y_2(t)$ das Intervall $1 \hspace{0.08cm} {\rm ms}$ ... $5 \hspace{0.08cm} \rm ms$.
- Damit beträgt in beiden Fällen die Messdauer $T_{\rm M} = 4 \hspace{0.08cm} \rm ms$.
- Es ist offensichtlich, dass bezüglich $y_1(t)$ die Parameter $\alpha = 1$ und $\tau = 0$ jeweils zur minimalen Verzerrungsleistung führen.
Das so genannte Signal–zu–Verzerrungs–Leistungsverhältnis berechnet sich im allgemeinen Fall zu
- $$\rho_{\rm V} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} \hspace{0.05cm}.$$
Hierbei bezeichnet
- $P_x$ die Leistung des Signals $x(t)$, und
- $\alpha^2 \cdot P_x$ die Leistung von $y(t) = \alpha \cdot x(t - \tau)$, die sich bei Abwesenheit von Verzerrungen ergeben würde.
Meist – so auch in dieser Aufgabe – wird dieses S/N-Verhältnis $\rho_{\rm V}$ logarithmisch in $\rm dB$ angegeben.
Hinweise:
- Die Aufgabe gehört zum Kapitel Klassifizierung der Verzerrungen.
- Berücksichtigen Sie insbesondere die Seiten
Fragebogen
Musterlösung
(1) Mit den gegebenen Parametern $\alpha = 1$ und $\tau= 0$ erhält man das in der Grafik dargestellte Fehlersignal $\varepsilon_1(t)$. Die Verzerrungsleistung ist somit gleich:
- $$P_{\rm V1} = \frac{ {1 \, \rm ms}}{4 \, \rm ms} \cdot \big[ ({0.1 \, \rm V})^2 + ({-0.1 \, \rm V})^2\big]\hspace{0.3cm}\Rightarrow \hspace{0.3cm}P_{\rm V1} \hspace{0.15cm}\underline{ = 5 \cdot 10^{-3} \, \rm V^2}. $$
(2) Die Leistung des Eingangssignals beträgt:
- $$P_{x} = \frac{1}{4 \, \rm ms} \cdot ({1 \, \rm V})^2 \cdot {4 \, \rm ms}\hspace{0.15cm}{ = {1 \, \rm V^2}}.$$
- Mit dem Ergebnis aus (1) erhält man somit für das Signal–zu–Verzerrungs–Leistungsverhältnis:
$$\rho_{\rm V1} = \frac{ P_{x}}{P_{\rm V1}}= \frac{ {1 \, \rm V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 200\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V1}\hspace{0.15cm}\underline{ = {23.01 \, \rm dB}}.$$
(3) Die Skizze auf dem Angabenblatt macht deutlich, dass sich auch ohne die auftretenden Verzerrungen – sondern allein durch Dämpfung und Laufzeit das Signal $y(t)$ von $x(t)$ – deutlich unterscheiden würde.
- Es würde sich $y(t) = 0.5 \cdot x(t-1\ {\rm ms}) $ ergeben.
- Wenn jemand diese Werte nicht sofort aus der Grafik erkennt, so müsste er für sehr (unendlich) viele $\alpha$– und $\tau$–Werte zunächst das Fehlersignal
- $$\varepsilon_2(t) = y_2(t) - \alpha \cdot x(t - \tau)$$
- und anschließend den mittleren quadratischen Fehler ermitteln, wobei das Integrationsintervall jeweils an $\tau$ anzupassen ist.
- Auch dann würde man das kleinstmögliche Ergebnis für $\alpha \; \underline{= 0.5}$ und $\tau \; \underline{= 1 \ \rm ms}$ erhalten. Für diese Optimierung von $\alpha$ und $\tau$ sollte man sich allerdings schon ein Computerprogramm gönnen.
(4) Die obige Skizze zeigt, dass $\varepsilon_2(t)$ bis auf eine Verschiebung um $1 \ \rm ms$ gleich dem Fehlersignal $\varepsilon_1(t)$ ist. Mit dem Integrationsintervall $1 \ {\rm ms}$ ... $5 \ {\rm ms}$ ergibt sich somit auch die gleiche Verzerrungsleistung:
- $$P_{\rm V2} = P_{\rm V1} \hspace{0.15cm}\underline{ = 5 \cdot 10^{-3} \, \rm V^2}.$$
(5) Entsprechend dem Angabenblatt gilt:
- $$\rho_{\rm V2} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V2}}= \frac{ 0.5^2 \cdot {1 \, \rm V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 50\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2} \hspace{0.15cm}\underline{= {16.99 \, \rm dB}}.$$
- Trotz gleicher Verzerrungsleistung ist $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2}$ gegenüber $10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V1}$ um etwa $6 \ \rm dB$ geringer.
- Das Signal $y_2(t)$ ist also hinsichtlich des SNR deutlich ungünstiger als $y_1(t)$.
- Es ist berücksichtigt, dass nun wegen $\alpha = 0.5$ die Leistung des Ausgangssignals nur noch ein Viertel der Eingangsleistung beträgt.
- Würde man diese Dämpfung am Ausgang durch eine Verstärkung um $1/\alpha$ kompensieren, so würde zwar die Verzerrungsleistung um $\alpha^2$ größer.
- Das Signal-zu-Verzerrungs-Leistungsverhältnis $\rho_{\rm V2}$ bliebe jedoch erhalten, weil auch das „Nutzsignal” um den gleichen Betrag angehoben wird.