Aufgaben:Aufgabe 3.6: PM oder FM? Oder AM?: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
Beachten Sie bei Ihrer Lösung, dass bei Winkelmodulation – dies ist der Sammelbegriff für Phasen– und Frequenzmodulation – der folgende Zusammenhang zwischen dem Modulationsindex $η$ und der Modulatorkonstanten $K_{\rm WM}$ besteht: | Beachten Sie bei Ihrer Lösung, dass bei Winkelmodulation – dies ist der Sammelbegriff für Phasen– und Frequenzmodulation – der folgende Zusammenhang zwischen dem Modulationsindex $η$ und der Modulatorkonstanten $K_{\rm WM}$ besteht: | ||
:$$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ {K_{\rm WM} \cdot A_{\rm N}}/({2 \pi \cdot f_{\rm N})} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$ | :$$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ {K_{\rm WM} \cdot A_{\rm N}}/({2 \pi \cdot f_{\rm N})} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$ | ||
| + | |||
| + | |||
| + | |||
| Zeile 30: | Zeile 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
{Um welchen Modulator handelt es sich? | {Um welchen Modulator handelt es sich? | ||
| − | |type=" | + | |type="()"} |
- AM–Modulator. | - AM–Modulator. | ||
- PM–Modulator. | - PM–Modulator. | ||
| Zeile 58: | Zeile 61: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig ist die <u>Antwort 3</u>: | '''(1)''' Richtig ist die <u>Antwort 3</u>: | ||
| − | *Da die Ortskurve einen Kreisbogen beschreibt, handelt es sich um einen Winkelmodulator (PM oder FM) mit dem Modulationsindex $η$. *Da aber hier $η$ offensichtlich von der Nachrichtenfrequenz $f_{\rm N}$ abhängt, kann eine Phasenmodulation ausgeschlossen werden. | + | *Da die Ortskurve einen Kreisbogen beschreibt, handelt es sich um einen Winkelmodulator (PM oder FM) mit dem Modulationsindex $η$. |
| + | *Da aber hier $η$ offensichtlich von der Nachrichtenfrequenz $f_{\rm N}$ abhängt, kann eine Phasenmodulation ausgeschlossen werden. | ||
| + | |||
| + | |||
| + | '''(2)''' Der Modulationsindex kann aus der Grafik abgelesen werden. Es gilt $η_1 = 75^\circ/180^\circ · π\hspace{0.15cm}\underline { ≈ 1.3}$. | ||
| − | |||
| Zeile 67: | Zeile 73: | ||
:$$ K_{\rm WM} = K_{\rm FM} = \frac{ 2 \pi \cdot f_{\rm N} \cdot \eta}{A_{\rm N}} = \frac{ 2 \pi \cdot 5 \cdot 10^3 \,\,{\rm Hz}\cdot 1.3}{2\,{\rm V}} \hspace{0.15cm}\underline {\approx 2.04 \cdot 10^4 \hspace{0.1cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$ | :$$ K_{\rm WM} = K_{\rm FM} = \frac{ 2 \pi \cdot f_{\rm N} \cdot \eta}{A_{\rm N}} = \frac{ 2 \pi \cdot 5 \cdot 10^3 \,\,{\rm Hz}\cdot 1.3}{2\,{\rm V}} \hspace{0.15cm}\underline {\approx 2.04 \cdot 10^4 \hspace{0.1cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' Der Frequenzmodulator kann als Phasenmodulator realisiert werden, wenn vorher das Quellensignal integriert wird. Dieses lautet: | + | |
| + | |||
| + | '''(4)''' Der Frequenzmodulator kann als Phasenmodulator realisiert werden, wenn vorher das Quellensignal integriert wird. Dieses lautet: | ||
:$$q_{\rm I}(t) = \int q(t)\hspace{0.15cm}{\rm d}t = A_{\rm N} \cdot\int \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.15cm}{\rm d}t =\frac{A_{\rm N}}{\omega_{\rm N}} \cdot \sin(\omega_{\rm N} \cdot t + \phi_{\rm N}) = \frac{A_{\rm N}}{\omega_{\rm N}} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N} - 90^\circ)\hspace{0.05cm}.$$ | :$$q_{\rm I}(t) = \int q(t)\hspace{0.15cm}{\rm d}t = A_{\rm N} \cdot\int \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.15cm}{\rm d}t =\frac{A_{\rm N}}{\omega_{\rm N}} \cdot \sin(\omega_{\rm N} \cdot t + \phi_{\rm N}) = \frac{A_{\rm N}}{\omega_{\rm N}} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N} - 90^\circ)\hspace{0.05cm}.$$ | ||
| − | Somit ergibt sich für das äquivalente | + | *Somit ergibt sich für das äquivalente Tiefpass-Signal mit $ϕ_{\rm N} = 30^\circ$: |
:$$s_{\rm TP}(t) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\omega_{\rm N} \hspace{0.03cm}\cdot \hspace{0.03cm}t \hspace{0.03cm} - \hspace{0.03cm}60^\circ)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm TP}(t = 0) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\hspace{0.03cm}60^\circ)} = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta /2}\hspace{0.05cm}.$$ | :$$s_{\rm TP}(t) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\omega_{\rm N} \hspace{0.03cm}\cdot \hspace{0.03cm}t \hspace{0.03cm} - \hspace{0.03cm}60^\circ)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm TP}(t = 0) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\hspace{0.03cm}60^\circ)} = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta /2}\hspace{0.05cm}.$$ | ||
| − | Der Nullphasenwinkel ist somit gleich $η/2$ entsprechend $ϕ_0\hspace{0.15cm}\underline {\approx 37.5^\circ}$. | + | *Der Nullphasenwinkel ist somit gleich $η/2$ entsprechend $ϕ_0\hspace{0.15cm}\underline {\approx 37.5^\circ}$. |
| + | |||
Aktuelle Version vom 27. März 2020, 16:46 Uhr
Zur Analyse eines Modulators wird an seinen Eingang das Signal
- $$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$
angelegt, wobei die Signalamplitude stets $A_{\rm N} = 2\ \rm V$ beträgt.
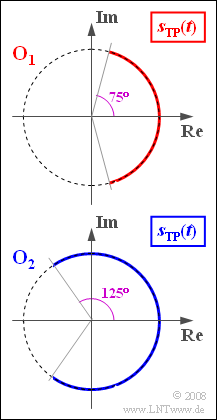
- Mit der Signalfrequenz $f_{\rm N} = f_1 = 5 \ \rm kHz$ wird die Ortskurve $\rm O_1$ ermittelt.
- Verwendet man die Nachrichtenfrequenz $f_{\rm N} = f_2$, so stellt sich die Ortskurve $\rm O_2$ ein.
Beachten Sie bei Ihrer Lösung, dass bei Winkelmodulation – dies ist der Sammelbegriff für Phasen– und Frequenzmodulation – der folgende Zusammenhang zwischen dem Modulationsindex $η$ und der Modulatorkonstanten $K_{\rm WM}$ besteht:
- $$\eta = \left\{ \begin{array}{c} K_{\rm WM} \cdot A_{\rm N} \\ {K_{\rm WM} \cdot A_{\rm N}}/({2 \pi \cdot f_{\rm N})} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm PM} \hspace{0.05cm}, \\ {\rm FM}. \hspace{0.05cm} \\ \end{array}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Frequenzmodulation.
- Bezug genommen wird aber auch auf das Kapitel Phasenmodulation.
Fragebogen
Musterlösung
- Da die Ortskurve einen Kreisbogen beschreibt, handelt es sich um einen Winkelmodulator (PM oder FM) mit dem Modulationsindex $η$.
- Da aber hier $η$ offensichtlich von der Nachrichtenfrequenz $f_{\rm N}$ abhängt, kann eine Phasenmodulation ausgeschlossen werden.
(2) Der Modulationsindex kann aus der Grafik abgelesen werden. Es gilt $η_1 = 75^\circ/180^\circ · π\hspace{0.15cm}\underline { ≈ 1.3}$.
(3) Bei Frequenzmodulation gilt:
- $$ K_{\rm WM} = K_{\rm FM} = \frac{ 2 \pi \cdot f_{\rm N} \cdot \eta}{A_{\rm N}} = \frac{ 2 \pi \cdot 5 \cdot 10^3 \,\,{\rm Hz}\cdot 1.3}{2\,{\rm V}} \hspace{0.15cm}\underline {\approx 2.04 \cdot 10^4 \hspace{0.1cm}{\rm V^{-1}}{\rm s^{-1}}}\hspace{0.05cm}.$$
(4) Der Frequenzmodulator kann als Phasenmodulator realisiert werden, wenn vorher das Quellensignal integriert wird. Dieses lautet:
- $$q_{\rm I}(t) = \int q(t)\hspace{0.15cm}{\rm d}t = A_{\rm N} \cdot\int \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.15cm}{\rm d}t =\frac{A_{\rm N}}{\omega_{\rm N}} \cdot \sin(\omega_{\rm N} \cdot t + \phi_{\rm N}) = \frac{A_{\rm N}}{\omega_{\rm N}} \cdot \cos(\omega_{\rm N} \cdot t + \phi_{\rm N} - 90^\circ)\hspace{0.05cm}.$$
- Somit ergibt sich für das äquivalente Tiefpass-Signal mit $ϕ_{\rm N} = 30^\circ$:
- $$s_{\rm TP}(t) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\omega_{\rm N} \hspace{0.03cm}\cdot \hspace{0.03cm}t \hspace{0.03cm} - \hspace{0.03cm}60^\circ)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}s_{\rm TP}(t = 0) = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta \hspace{0.03cm}\cdot \hspace{0.05cm}\cos(\hspace{0.03cm}60^\circ)} = {\rm e}^{{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\eta /2}\hspace{0.05cm}.$$
- Der Nullphasenwinkel ist somit gleich $η/2$ entsprechend $ϕ_0\hspace{0.15cm}\underline {\approx 37.5^\circ}$.
(5) Aus der Definition des Modulationsindex bei Frequenzmodulation folgt:
- $$\eta_1 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 1}}\hspace{0.05cm},\hspace{0.3cm} \eta_2 = \frac{K_{\rm WM} \cdot A_{\rm N}}{2 \pi \cdot f_{\rm 2}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\frac{\eta_1}{\eta_2} = \frac{f_2}{f_1}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} f_2 = \frac{\eta_1}{\eta_2} \cdot f_1 = \frac{75^\circ}{125^\circ} \cdot 5\,{\rm kHz} \hspace{0.15cm}\underline {= 3\,{\rm kHz}}\hspace{0.05cm}.$$