Aufgaben:Aufgabe 5.7Z: Anwendung der IDFT: Unterschied zwischen den Versionen
Aus LNTwww
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
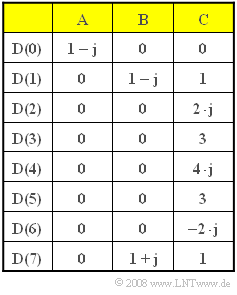
| − | [[Datei:P_ID1670__Mod_Z_5_7.png|right|frame|Drei Sätze $\rm A$, $\rm B$ und $\rm C$ für die Spektralkoeffizienten]] | + | [[Datei:P_ID1670__Mod_Z_5_7.png|right|frame|Drei Sätze $\rm A$, $\rm B$ und $\rm C$ <br>für die Spektralkoeffizienten]] |
| − | Bei der [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskreten Fouriertransformation]] (DFT) werden aus den Zeitabtastwerten $d(ν)$ mit der Laufvariablen $ν = 0$, ... , $N – 1$ die diskreten Spektralkoeffizienten $D(μ)$ mit $μ = 0$, ... , $N – 1$ wie folgt berechnet: | + | Bei der [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskreten Fouriertransformation]] $\rm (DFT)$ werden aus den Zeitabtastwerten $d(ν)$ mit der Laufvariablen $ν = 0$, ... , $N – 1$ die diskreten Spektralkoeffizienten $D(μ)$ mit $μ = 0$, ... , $N – 1$ wie folgt berechnet: |
:$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | :$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| − | Hierbei ist mit $w$ der komplexe Drehfaktor abgekürzt, der wie folgt definiert ist: | + | Hierbei ist mit $w$ der komplexe Drehfaktor abgekürzt, der wie folgt definiert ist: |
:$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ | :$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$ | ||
| − | Entsprechend gilt für die [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)#Inverse_Diskrete_Fouriertransformation|Inverse Diskrete Fouriertransformation]] (IDFT) quasi als „Umkehrfunktion” der DFT: | + | Entsprechend gilt für die [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)#Inverse_Diskrete_Fouriertransformation|Inverse Diskrete Fouriertransformation]] $\rm (IDFT)$ quasi als „Umkehrfunktion” der DFT: |
:$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | :$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$ | ||
| − | In dieser Aufgabe sollen für verschiedene komplexwertige Beispielfolgen $D(μ)$ – die in der Tabelle mit $\rm A$, $\rm B$ und $\rm C$ bezeichnet sind – die Zeitkoeffizienten $d(ν)$ ermittelt werden. Es gilt somit stets $N = 8$. | + | In dieser Aufgabe sollen für verschiedene komplexwertige Beispielfolgen $D(μ)$ – die in der Tabelle mit $\rm A$, $\rm B$ und $\rm C$ bezeichnet sind – die Zeitkoeffizienten $d(ν)$ ermittelt werden. Es gilt somit stets $N = 8$. |
| − | + | Hinweise: | |
| − | |||
| − | |||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Realisierung_von_OFDM-Systemen|Realisierung von OFDM-Systemen]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Realisierung_von_OFDM-Systemen|Realisierung von OFDM-Systemen]]. | ||
*Bezug genommen wird auch auf das Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation]] im Buch „Signaldarstellung”. | *Bezug genommen wird auch auf das Kapitel [[Signaldarstellung/Diskrete_Fouriertransformation_(DFT)|Diskrete Fouriertransformation]] im Buch „Signaldarstellung”. | ||
| − | *Sie können Ihre Ergebnisse mit dem interaktiven Applet [[Applets: | + | *Sie können Ihre Ergebnisse mit dem interaktiven Applet [[Applets:Diskrete_Fouriertransformation_und_Inverse|Diskrete Fouriertransformation und Inverse]] kontrollieren. |
| Zeile 47: | Zeile 45: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Wegen $D(μ) = 0$ für $μ ≠ 0$ sind alle Zeitkoeffizienten $d(ν) = D(0)= 1 - {\rm j}$. Damit gilt auch: | + | '''(1)''' Wegen $D(μ) = 0$ für $μ ≠ 0$ sind alle Zeitkoeffizienten $d(ν) = D(0)= 1 - {\rm j}$. Damit gilt auch: |
:$${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$ | :$${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$ | ||
| − | '''(2)''' Hier sind alle Spektralkoeffizienten Null mit Ausnahme von $D_1 = 1 - {\rm j}$ und $D_7 = 1 + {\rm j}$. Daraus folgt für alle Zeitkoeffizienten ( | + | '''(2)''' Hier sind alle Spektralkoeffizienten Null mit Ausnahme von $D_1 = 1 - {\rm j}$ und $D_7 = 1 + {\rm j}$. |
| + | *Daraus folgt für alle Zeitkoeffizienten $(0 ≤ ν ≤ 7)$: | ||
:$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ | :$$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$ | ||
*Aufgrund der Periodizität gilt aber auch: | *Aufgrund der Periodizität gilt aber auch: | ||
| Zeile 58: | Zeile 57: | ||
*Mit dem Satz von Euler lässt sich dieser Ausdruck wie folgt umformen: | *Mit dem Satz von Euler lässt sich dieser Ausdruck wie folgt umformen: | ||
:$$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$ | :$$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$ | ||
| − | *Diese Zeitfunktion $d(ν)$ ist rein reell und kennzeichnet eine harmonische Schwingung mit der Amplitude $ 2 \cdot \sqrt{2}$ und der Phase $φ = 45^\circ$. | + | *Diese Zeitfunktion $d(ν)$ ist rein reell und kennzeichnet eine harmonische Schwingung mit der Amplitude $ 2 \cdot \sqrt{2}$ und der Phase $φ = 45^\circ$. |
| − | *Der Zeitkoeffizient mit Index $ν = 1$ gibt das Maximum an: | + | *Der Zeitkoeffizient mit Index $ν = 1$ gibt das Maximum an: |
:$$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$ | :$$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$ | ||
Aktuelle Version vom 12. Januar 2022, 09:48 Uhr
Drei Sätze $\rm A$, $\rm B$ und $\rm C$
für die Spektralkoeffizienten
für die Spektralkoeffizienten
Bei der Diskreten Fouriertransformation $\rm (DFT)$ werden aus den Zeitabtastwerten $d(ν)$ mit der Laufvariablen $ν = 0$, ... , $N – 1$ die diskreten Spektralkoeffizienten $D(μ)$ mit $μ = 0$, ... , $N – 1$ wie folgt berechnet:
- $$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
Hierbei ist mit $w$ der komplexe Drehfaktor abgekürzt, der wie folgt definiert ist:
- $$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$
Entsprechend gilt für die Inverse Diskrete Fouriertransformation $\rm (IDFT)$ quasi als „Umkehrfunktion” der DFT:
- $$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.08cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$
In dieser Aufgabe sollen für verschiedene komplexwertige Beispielfolgen $D(μ)$ – die in der Tabelle mit $\rm A$, $\rm B$ und $\rm C$ bezeichnet sind – die Zeitkoeffizienten $d(ν)$ ermittelt werden. Es gilt somit stets $N = 8$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Realisierung von OFDM-Systemen.
- Bezug genommen wird auch auf das Kapitel Diskrete Fouriertransformation im Buch „Signaldarstellung”.
- Sie können Ihre Ergebnisse mit dem interaktiven Applet Diskrete Fouriertransformation und Inverse kontrollieren.
Fragebogen
Musterlösung
(1) Wegen $D(μ) = 0$ für $μ ≠ 0$ sind alle Zeitkoeffizienten $d(ν) = D(0)= 1 - {\rm j}$. Damit gilt auch:
- $${\rm Re}[d(1)] \hspace{0.15cm}\underline {=+ 1}, \hspace{0.3cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= -1}.$$
(2) Hier sind alle Spektralkoeffizienten Null mit Ausnahme von $D_1 = 1 - {\rm j}$ und $D_7 = 1 + {\rm j}$.
- Daraus folgt für alle Zeitkoeffizienten $(0 ≤ ν ≤ 7)$:
- $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {7\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}.$$
- Aufgrund der Periodizität gilt aber auch:
- $$d(\nu) = (1 - {\rm j}) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} +(1 + {\rm j}) \cdot {\rm{e}}^{ +{\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}= \left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} + {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right]+ {\rm{j}} \cdot\left[ {\rm{e}}^{ + {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu} - {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\nu}\right].$$
- Mit dem Satz von Euler lässt sich dieser Ausdruck wie folgt umformen:
- $$d(\nu) = 2 \cdot \cos \left( {\pi}/{4}\cdot \nu \right)+ 2 \cdot \sin \left( {\pi}/{4}\cdot \nu \right).$$
- Diese Zeitfunktion $d(ν)$ ist rein reell und kennzeichnet eine harmonische Schwingung mit der Amplitude $ 2 \cdot \sqrt{2}$ und der Phase $φ = 45^\circ$.
- Der Zeitkoeffizient mit Index $ν = 1$ gibt das Maximum an:
- $$ {\rm Re}[d(1)] = 2 \cdot \frac {\sqrt{2}}{2}+ 2 \cdot \frac {\sqrt{2}}{2} = 2 \cdot {\sqrt{2}} \hspace{0.15cm}\underline {\approx 2.828}, \hspace{0.5cm}{\rm Im}[d(1)] \hspace{0.15cm}\underline {= 0}.$$
(3) Entsprechend der allgemeinen Gleichung gilt:
- $$d(1) = \sum\limits_{\mu = 0}^{7} D(\mu)\cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}/4\hspace{0.04cm}\cdot \hspace{0.04cm}\mu} = \left[ D(1) + D(7) \right]\cdot \cos \left( {\pi}/{4} \right) + \left[ D(3) + D(5) \right]\cdot \cos \left( {3\pi}/{4} \right)+ {\rm j} \cdot \left[ D(2) - D(6) \right]\cdot \sin \left( {\pi}/{2} \right) + D(4) \cdot {\rm{e}}^{ - {\rm{j}}\hspace{0.04cm}\cdot \hspace{0.04cm} {\rm{\pi}}}.$$
- Die ersten drei Terme liefern rein reelle Ergebnisse:
- $${\rm Re}[d(1)] = (1+1) \cdot \frac{1}{\sqrt{2}}-(3+3) \cdot \frac{1}{\sqrt{2}}+ {\rm j} \cdot4{\rm j} \cdot 1 = -\frac{4}{\sqrt{2}}-4\hspace{0.15cm}\underline { \approx -6.829}.$$
- Für den Imaginärteil ergibt sich:
- $${\rm Im}[d(1)] = {\rm Im}\left[4 \cdot{\rm j} \cdot (-1) \right] \hspace{0.15cm}\underline {= -4}.$$
