Aufgaben:Aufgabe 2.7Z: Leistungsdichtespektren der Pseudoternärcodes: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
| − | [[Datei:P_ID1354__Dig_Z_2_7.png|right|frame|Leistungsdichtespektren drei | + | [[Datei:P_ID1354__Dig_Z_2_7.png|right|frame|Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes]] |
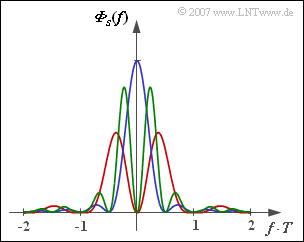
In der Grafik sehen Sie die Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes, die sich aus der allgemeinen Beschreibung gemäß der [[Aufgaben:2.7_AMI-Code|Aufgabe 2.7]] durch unterschiedliche Werte der Parameter $N_{\rm C}$ und $K_{\rm C}$ ergeben. In verschiedenen Farben sind die Leistungsdichtespektren | In der Grafik sehen Sie die Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes, die sich aus der allgemeinen Beschreibung gemäß der [[Aufgaben:2.7_AMI-Code|Aufgabe 2.7]] durch unterschiedliche Werte der Parameter $N_{\rm C}$ und $K_{\rm C}$ ergeben. In verschiedenen Farben sind die Leistungsdichtespektren | ||
| − | :$${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \ | + | :$${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$ |
für folgende Varianten dargestellt: | für folgende Varianten dargestellt: | ||
*AMI–Code $(N_{\rm C} = 1, K_{\rm C} = +1)$, | *AMI–Code $(N_{\rm C} = 1, K_{\rm C} = +1)$, | ||
| Zeile 16: | Zeile 16: | ||
Alle hier betrachteten Pseudoternärcodes besitzen die gleiche Wahrscheinlichkeitsverteilung: | Alle hier betrachteten Pseudoternärcodes besitzen die gleiche Wahrscheinlichkeitsverteilung: | ||
| − | :$${\rm Pr}[s(t) = 0]= {1}/{2},\hspace{0.2cm}{\rm Pr}[s(t) = +s_0]= {\rm Pr}[s(t) = -s_0]={1}/{4}\hspace{0.05cm}.$$ | + | :$${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$ |
| Zeile 52: | Zeile 52: | ||
+ grün. | + grün. | ||
| − | {Welcher Code besitzt die größte Sendeleistung?|type="[]"} | + | {Welcher Code besitzt die größte Sendeleistung? |
| − | - AMI–Code | + | |type="[]"} |
| − | - Duobinärcode | + | - AMI–Code, |
| + | - Duobinärcode, | ||
- Bipolarcode 2. Ordnung. | - Bipolarcode 2. Ordnung. | ||
+ Die Sendeleistung ist bei allen Codes gleich. | + Die Sendeleistung ist bei allen Codes gleich. | ||
| Zeile 60: | Zeile 61: | ||
{Welcher dieser Codes ist gleichsignalfrei? | {Welcher dieser Codes ist gleichsignalfrei? | ||
|type="[]"} | |type="[]"} | ||
| − | + AMI–Code | + | + AMI–Code, |
| − | - Duobinärcode | + | - Duobinärcode, |
+ Bipolarcode 2. Ordnung. | + Bipolarcode 2. Ordnung. | ||
| Zeile 88: | Zeile 89: | ||
| − | '''(4)''' Die Sendeleistung $P_{\rm S}$ ist gleich dem Integral über das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ und ist für alle hier betrachteten Codes gleich ⇒ <u>Lösungsvorschlag 4</u>. Dies folgt auch aus der Leistungsberechnung durch Scharmittelung: | + | '''(4)''' Die Sendeleistung $P_{\rm S}$ ist gleich dem Integral über das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ und ist für alle hier betrachteten Codes gleich ⇒ <u>Lösungsvorschlag 4</u>. |
| + | *Dies folgt auch aus der Leistungsberechnung durch Scharmittelung: | ||
:$$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$ | :$$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$ | ||
| + | |||
'''(5)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | '''(5)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
*Gleichsignalfreiheit liegt vor, wenn das Leistungsdichtespektrum bei der Frequenz $f = 0$ keinen Anteil aufweist. | *Gleichsignalfreiheit liegt vor, wenn das Leistungsdichtespektrum bei der Frequenz $f = 0$ keinen Anteil aufweist. | ||
| − | *Dies gilt für den AMI–Code und den Bipolarcode zweiter Ordnung | + | *Dies gilt für den AMI–Code und den Bipolarcode zweiter Ordnung. |
*Diese Aussage bedeutet nicht nur, dass $s(t)$ keinen Gleichanteil besitzt, also dass ${\it \Phi}_{s}(f)$ keine Diracfunktion bei $f = 0$ besitzt. | *Diese Aussage bedeutet nicht nur, dass $s(t)$ keinen Gleichanteil besitzt, also dass ${\it \Phi}_{s}(f)$ keine Diracfunktion bei $f = 0$ besitzt. | ||
| − | *Es bedeutet darüber hinaus auch, dass der kontinuierliche LDS–Anteil bei $f = 0$ verschwindet. Dies wird genau dann erreicht, wenn sowohl die lange „$+1$”– als auch die lange „$–1$”–Folge durch die Codiervorschrift ausgeschlossen werden. | + | *Es bedeutet darüber hinaus auch, dass der kontinuierliche LDS–Anteil bei $f = 0$ verschwindet. |
| + | *Dies wird genau dann erreicht, wenn sowohl die lange „$+1$”– als auch die lange „$–1$”–Folge durch die Codiervorschrift ausgeschlossen werden. | ||
Aktuelle Version vom 14. Februar 2019, 14:26 Uhr
In der Grafik sehen Sie die Leistungsdichtespektren von drei verschiedenen Pseudoternärcodes, die sich aus der allgemeinen Beschreibung gemäß der Aufgabe 2.7 durch unterschiedliche Werte der Parameter $N_{\rm C}$ und $K_{\rm C}$ ergeben. In verschiedenen Farben sind die Leistungsdichtespektren
- $${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$
für folgende Varianten dargestellt:
- AMI–Code $(N_{\rm C} = 1, K_{\rm C} = +1)$,
- Duobinärcode $(N_{\rm C} = 1, K_{\rm C} = -1)$,
- Bipolarcode zweiter Ordnung $ (N_{\rm C} = 2, K_{\rm C} = +1)$.
Bei obiger LDS–Gleichung ist die Verwendung von rechteckförmigen NRZ–Sendegrundimpulsen vorausgesetzt.
Alle hier betrachteten Pseudoternärcodes besitzen die gleiche Wahrscheinlichkeitsverteilung:
- $${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Symbolweise Codierung mit Pseudoternärcodes.
- Sie können die Ergebnisse mit dem interaktiven Applet Signale, AKF und LDS der Pseudoternärcodes überprüfen.
Fragebogen
Musterlösung
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
Dieser Kurvenverlauf ist rot dargestellt. Das LDS der Amplitudenkoeffizienten ist ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$.
(2) Nach Umformung erhält man für den Duobinärcode:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
In der Grafik ist der Duobinärcode blau gezeichnet. Weiterhin gilt ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$.
(3) Der Bipolarcode zweiter Ordnung unterscheidet sich vom AMI–Code nur durch den Faktor $2$ im Argument der $\sin^{2}$–Funktion:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
Der grüne Kurvenzug stellt diesen Funktionsverlauf dar. Gegenüber dem AMI-Code ist ${\it \Phi}_{a}(f)$ genau halb so breit.
(4) Die Sendeleistung $P_{\rm S}$ ist gleich dem Integral über das Leistungsdichtespektrum ${\it \Phi}_{s}(f)$ und ist für alle hier betrachteten Codes gleich ⇒ Lösungsvorschlag 4.
- Dies folgt auch aus der Leistungsberechnung durch Scharmittelung:
- $$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$
(5) Richtig sind die Lösungsvorschläge 1 und 3:
- Gleichsignalfreiheit liegt vor, wenn das Leistungsdichtespektrum bei der Frequenz $f = 0$ keinen Anteil aufweist.
- Dies gilt für den AMI–Code und den Bipolarcode zweiter Ordnung.
- Diese Aussage bedeutet nicht nur, dass $s(t)$ keinen Gleichanteil besitzt, also dass ${\it \Phi}_{s}(f)$ keine Diracfunktion bei $f = 0$ besitzt.
- Es bedeutet darüber hinaus auch, dass der kontinuierliche LDS–Anteil bei $f = 0$ verschwindet.
- Dies wird genau dann erreicht, wenn sowohl die lange „$+1$”– als auch die lange „$–1$”–Folge durch die Codiervorschrift ausgeschlossen werden.
(6) Beide vorgegebenen Lösungsvorschläge treffen in der Praxis zu.