Aufgaben:Aufgabe 4.06: Optimale Entscheidungsgrenzen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Datei:P_ID2015__Dig_A_4_6.png|right|frame|Signalraumkonstellation mit<br> $N = 2, \ M = 2$]] | [[Datei:P_ID2015__Dig_A_4_6.png|right|frame|Signalraumkonstellation mit<br> $N = 2, \ M = 2$]] | ||
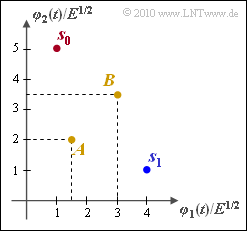
| − | Wie betrachten ein binäres Nachrichtensystem $(M = 2)$, das durch die gezeichnete 2D–Signalraumkonstellation $(N = 2)$ festliegt. Für die beiden möglichen Sendevektoren, die mit den Nachrichten $m_0$ und $m_1$ direkt gekoppelt sind, gilt: | + | Wie betrachten ein binäres Nachrichtensystem $(M = 2)$, das durch die gezeichnete 2D–Signalraumkonstellation $(N = 2)$ festliegt. Für die beiden möglichen Sendevektoren, die mit den Nachrichten $m_0$ und $m_1$ direkt gekoppelt sind, gilt: |
:$$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$ | :$$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$ | ||
:$$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$ | :$$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$ | ||
| − | Gesucht ist jeweils die optimale Entscheidungsgrenze zwischen den Regionen $I_0 ⇔ m_0$ und $I_1 ⇔ m_1$, wobei von folgenden Voraussetzungen ausgegangen wird: | + | Gesucht ist jeweils die optimale Entscheidungsgrenze zwischen den Regionen $I_0 ⇔ m_0$ und $I_1 ⇔ m_1$, wobei von folgenden Voraussetzungen ausgegangen wird: |
| − | * Für die Teilaufgaben '''(1)''' bis '''(3)''' gilt | + | * Für die Teilaufgaben '''(1)''' bis '''(3)''' gilt: |
:$${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 | :$${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * Für die Teilaufgaben '''(4)''' und '''(5)''' soll dagegen gelten: | + | * Für die Teilaufgaben '''(4)''' und '''(5)''' soll dagegen gelten: |
:$${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} | :$${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | \Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
| Zeile 17: | Zeile 17: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Bei AWGN–Rauschen mit Varianz $\sigma_n^2$ ist die Entscheidungsgrenze die Lösung folgender vektoriellen Gleichung hinsichtlich des Vektors $(\rho_1, \rho_2)$: | + | Bei AWGN–Rauschen mit Varianz $\sigma_n^2$ ist die Entscheidungsgrenze die Lösung folgender vektoriellen Gleichung hinsichtlich des Vektors $\boldsymbol{ \rho } = (\rho_1, \rho_2)$: |
:$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | :$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
| − | 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0 | + | 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ |
| − | |||
Zusätzlich sind in der Grafik zwei Empfangswerte | Zusätzlich sind in der Grafik zwei Empfangswerte | ||
| − | :$$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm}, | + | :$$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm},$$ |
| + | :$$\boldsymbol{ B }= \sqrt {E} \cdot (3, \hspace{0.1cm}3.5) $$ | ||
| − | eingezeichnet. Es ist zu überprüfen, ob diese bei den entsprechenden Randbedingungen den Regionen $I_0$ $($und damit der Nachricht $m_0)$ oder $I_1$ $($Nachricht $m_1)$ zugeordnet werden sollten. | + | eingezeichnet. Es ist zu überprüfen, ob diese bei den entsprechenden Randbedingungen den Regionen $I_0$ $($und damit der Nachricht $m_0)$ oder $I_1$ $($Nachricht $m_1)$ zugeordnet werden sollten. |
| Zeile 31: | Zeile 31: | ||
| − | + | Hinweise: | |
| − | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| Approximation der Fehlerwahrscheinlichkeit]]. | + | * Die Aufgabe gehört zum Kapitel [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit| "Approximation der Fehlerwahrscheinlichkeit"]]. |
| + | |||
* Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden. | * Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden. | ||
| Zeile 40: | Zeile 41: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wo liegt die optimale Entscheidergrenze bei gleichwahrscheinlichen Symbolen? Bei | + | {Wo liegt die optimale Entscheidergrenze bei gleichwahrscheinlichen Symbolen? Bei |
|type="[]"} | |type="[]"} | ||
+ $\rho_2 = 3/4 \cdot \rho_1 + 9/8$, | + $\rho_2 = 3/4 \cdot \rho_1 + 9/8$, | ||
| Zeile 56: | Zeile 57: | ||
- zum Entscheidungsgebiet $I_1$. | - zum Entscheidungsgebiet $I_1$. | ||
| − | {Wie lautet die Gleichung der Entscheidungsgeraden für ${\rm Pr}(m_0) = 0.817, \sigma_n = 1$? | + | {Wie lautet die Gleichung der Entscheidungsgeraden für ${\rm Pr}(m_0) = 0.817,\ \sigma_n = 1$? |
| − | |type=" | + | |type="()"} |
- $\rho_2 = 3/4 \cdot \rho_1 + 9/8$, | - $\rho_2 = 3/4 \cdot \rho_1 + 9/8$, | ||
+ $\rho_2 = 3/4 \cdot \rho_1 + 3/4$, | + $\rho_2 = 3/4 \cdot \rho_1 + 3/4$, | ||
| Zeile 73: | Zeile 74: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Mit ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$ lautet die Gleichung der Begrenzungsgeraden zwischen den Entscheidungsgebieten $I_0$ und $I_1$: | + | '''(1)''' Mit ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$ lautet die Gleichung der Begrenzungsgeraden zwischen den Entscheidungsgebieten $I_0$ und $I_1$: |
:$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 = | :$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 = | ||
2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ | 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ | ||
| − | Mit den gegebenen Vektorwerten, also den Zahlenwerten | + | *Mit den gegebenen Vektorwerten, also den Zahlenwerten |
:$$|| \boldsymbol{ s }_1||^2 = 4^2 + 1^2 = 17\hspace{0.05cm}, \hspace{0.2cm} | :$$|| \boldsymbol{ s }_1||^2 = 4^2 + 1^2 = 17\hspace{0.05cm}, \hspace{0.2cm} | ||
|| \boldsymbol{ s }_0||^2 = 1^2 + 5^2 = 26\hspace{0.05cm}, \hspace{0.2cm} | || \boldsymbol{ s }_0||^2 = 1^2 + 5^2 = 26\hspace{0.05cm}, \hspace{0.2cm} | ||
\boldsymbol{ s }_1 - \boldsymbol{ s }_0 = (3,\hspace{0.1cm}-4) \hspace{0.05cm}$$ | \boldsymbol{ s }_1 - \boldsymbol{ s }_0 = (3,\hspace{0.1cm}-4) \hspace{0.05cm}$$ | ||
| − | erhält man folgende Gleichung für die Entscheidungsgrenzen: | + | :erhält man folgende Gleichung für die Entscheidungsgrenzen: |
:$$3 \cdot \rho_1 - 4 \cdot \rho_2 = ({17-26})/{2} = - {9}/{2} | :$$3 \cdot \rho_1 - 4 \cdot \rho_2 = ({17-26})/{2} = - {9}/{2} | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\rho_2 = 3/4 \cdot \rho_1 + 9/8 | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\rho_2 = 3/4 \cdot \rho_1 + 9/8 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | [[Datei:P_ID2033__Dig_A_4_6a.png|right|frame|Entscheidungsgerade und Entscheidungsregionen]] | + | [[Datei:P_ID2033__Dig_A_4_6a.png|right|frame|Entscheidungsgerade und Entscheidungsregionen für $K=0$]] |
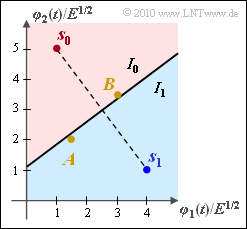
| − | Die Entscheidungsgrenze liegt in der Mitte zwischen $s_0$ und $s_1$ und verläuft um $90^\circ$ gedreht gegenüber der Verbindungslinie zwischen den beiden Symbolen. Sie geht durch den Punkt $(2.5, \ \, 3)$. Richtig ist also der <u>erste Lösungsvorschlag</u>. | + | *Die Entscheidungsgrenze liegt in der Mitte zwischen $s_0$ und $s_1$ und verläuft um $90^\circ$ gedreht gegenüber der Verbindungslinie zwischen den beiden Symbolen. |
| + | *Sie geht durch den Punkt $(2.5, \ \, 3)$. Richtig ist also der <u>erste Lösungsvorschlag</u>. | ||
| + | *Der Vorschlag 2 beschreibt dagegen die Verbindungsgerade selbst und $\rho_2 = 3$ ist eine Horizontale. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Das Entscheidungsgebiet $I_1$ sollte natürlich den Punkt $s_1$ beinhalten ⇒ Gebiet unterhalb der Entscheidungsgeraden. | ||
| + | *Punkt $A = (1.5, \ \, 2)$ gehört zu diesem Entscheidungsgebiet, wie aus der Grafik hervorgeht. | ||
| + | *Rechnerisch lässt sich dies zeigen, da die Entscheidungsgerade zum Beispiel durch den Punkt $(1.5, \ \, 2.25)$ geht und somit $(1.5, \ \, 2)$ unterhalb der Entscheidungsgeraden liegt. | ||
| + | *Richtig ist also der <u>Lösungsvorschlag 2</u>. | ||
| + | |||
| − | |||
| − | '''( | + | '''(3)''' Die Entscheidungsgerade geht auch durch den Punkt $(3, \ \, 3.375)$. |
| + | *$B = (3, \ \, 3.5)$ liegt oberhalb und gehört somit zum Entscheidungsgebiet $I_0$ entsprechend dem <u>Lösungsvorschlag 1</u>. | ||
| − | |||
| − | '''(4)''' Entsprechend der Gleichung auf dem Angabenblatt und den Berechnungen zur Teilaufgabe (1) gilt nun: | + | '''(4)''' Entsprechend der Gleichung auf dem Angabenblatt und den Berechnungen zur Teilaufgabe '''(1)''' gilt nun: |
| − | [[Datei:P_ID2034__Dig_A_4_6c.png|right|frame|Entscheidungsgebiete für verschiedene | + | [[Datei:P_ID2034__Dig_A_4_6c.png|right|frame|Entscheidungsgebiete für verschiedene $K$–Werte]] |
:$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | :$$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ | 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ | ||
| − | Mit $|| \boldsymbol{ s }_1||^2 = 17$, $|| \boldsymbol{ s }_0||^2 = 26$, $ \boldsymbol{ s }_1 \, –\boldsymbol{ s }_0 = (3, \ \, –4)$ erhält man: | + | *Mit $|| \boldsymbol{ s }_1||^2 = 17$, $|| \boldsymbol{ s }_0||^2 = 26$, $ \boldsymbol{ s }_1 \, –\boldsymbol{ s }_0 = (3, \ \, –4)$ erhält man: |
:$$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - K /8 | :$$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - K /8 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Hierbei ist folgende Abkürzung verwendet worden: | + | *Hierbei ist folgende Abkürzung verwendet worden: |
:$$K = 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | :$$K = 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = | ||
2 \cdot 1^2 \cdot 1.5 = 3 \hspace{0.05cm}.$$ | 2 \cdot 1^2 \cdot 1.5 = 3 \hspace{0.05cm}.$$ | ||
| − | Daraus folgt weiter: | + | *Daraus folgt weiter: |
:$$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - 3 /8 = 3/4 \cdot \rho_1 + 3/4 | :$$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - 3 /8 = 3/4 \cdot \rho_1 + 3/4 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
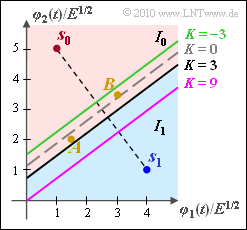
| − | Die Entscheidungsgerade ist um $3/8$ nach unten verschoben (schwarze Kurve, mit & | + | *Die Entscheidungsgerade ist um $3/8$ nach unten verschoben $($schwarze Kurve, mit "$K = 3$" bezeichnet in der Grafik$)$. |
| + | * Richtig ist also der <u>Lösungsvorschlag 2</u>. | ||
| − | + | #Die erste Gleichung beschreibt die optimale Entscheidungsgrenze für gleichwahrscheinliche Symbole $(K = 0$, grau gestrichelt$)$. | |
| − | + | #Die dritte Gleichung gilt für $K = \, –3$. Diese ergibt sich mit $\sigma_n^2 = 1$ für die Symbolwahrscheinlichkeiten ${\rm Pr}(m_1) \approx 0.817$, ${\rm Pr}(m_0) \approx 0.138$ $($grüne Kurve$)$. | |
| − | + | #Die violette Gerade ergibt sich mit $K = 9$, also zum Beispiel bei gleichen Wahrscheinlichkeiten wie für die schwarze Kurve, aber nun mit der Varianz $\sigma_n^2 = 3$. | |
| − | '''(5)''' Bereits aus obiger Grafik erkennt man, dass nun sowohl $A$ als auch $B$ zur Entscheidungsregion $I_0$ gehören. Richtig sind also die <u>Lösungsvorschläge 1 und 3</u>. | + | '''(5)''' Bereits aus obiger Grafik erkennt man, dass nun sowohl $A$ als auch $B$ zur Entscheidungsregion $I_0$ gehören. Richtig sind also die <u>Lösungsvorschläge 1 und 3</u>. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 27. Juli 2022, 16:47 Uhr
Wie betrachten ein binäres Nachrichtensystem $(M = 2)$, das durch die gezeichnete 2D–Signalraumkonstellation $(N = 2)$ festliegt. Für die beiden möglichen Sendevektoren, die mit den Nachrichten $m_0$ und $m_1$ direkt gekoppelt sind, gilt:
- $$\boldsymbol{ s }_0 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (1,\hspace{0.1cm} 5) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_0 \hspace{0.05cm},$$
- $$ \boldsymbol{ s }_1 \hspace{-0.1cm} \ =\ \hspace{-0.1cm} \sqrt {E} \cdot (4, \hspace{0.1cm}1) \hspace{0.2cm} \Leftrightarrow \hspace{0.2cm} m_1 \hspace{0.05cm}.$$
Gesucht ist jeweils die optimale Entscheidungsgrenze zwischen den Regionen $I_0 ⇔ m_0$ und $I_1 ⇔ m_1$, wobei von folgenden Voraussetzungen ausgegangen wird:
- Für die Teilaufgaben (1) bis (3) gilt:
- $${\rm Pr}(m_0 ) = {\rm Pr}(m_1 ) = 0.5 \hspace{0.05cm}. $$
- Für die Teilaufgaben (4) und (5) soll dagegen gelten:
- $${\rm Pr}(m_0 ) = 0.817 \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_1 ) = 0.183\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 1.5 \hspace{0.05cm}.$$
Bei AWGN–Rauschen mit Varianz $\sigma_n^2$ ist die Entscheidungsgrenze die Lösung folgender vektoriellen Gleichung hinsichtlich des Vektors $\boldsymbol{ \rho } = (\rho_1, \rho_2)$:
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
Zusätzlich sind in der Grafik zwei Empfangswerte
- $$\boldsymbol{ A }= \sqrt {E} \cdot (1.5, \hspace{0.1cm}2)\hspace{0.05cm},$$
- $$\boldsymbol{ B }= \sqrt {E} \cdot (3, \hspace{0.1cm}3.5) $$
eingezeichnet. Es ist zu überprüfen, ob diese bei den entsprechenden Randbedingungen den Regionen $I_0$ $($und damit der Nachricht $m_0)$ oder $I_1$ $($Nachricht $m_1)$ zugeordnet werden sollten.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Approximation der Fehlerwahrscheinlichkeit".
- Für numerische Berechnungen kann zur Vereinfachung die Energie $E = 1$ gesetzt werden.
Fragebogen
Musterlösung
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
- Mit den gegebenen Vektorwerten, also den Zahlenwerten
- $$|| \boldsymbol{ s }_1||^2 = 4^2 + 1^2 = 17\hspace{0.05cm}, \hspace{0.2cm} || \boldsymbol{ s }_0||^2 = 1^2 + 5^2 = 26\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 - \boldsymbol{ s }_0 = (3,\hspace{0.1cm}-4) \hspace{0.05cm}$$
- erhält man folgende Gleichung für die Entscheidungsgrenzen:
- $$3 \cdot \rho_1 - 4 \cdot \rho_2 = ({17-26})/{2} = - {9}/{2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\rho_2 = 3/4 \cdot \rho_1 + 9/8 \hspace{0.05cm}.$$
- Die Entscheidungsgrenze liegt in der Mitte zwischen $s_0$ und $s_1$ und verläuft um $90^\circ$ gedreht gegenüber der Verbindungslinie zwischen den beiden Symbolen.
- Sie geht durch den Punkt $(2.5, \ \, 3)$. Richtig ist also der erste Lösungsvorschlag.
- Der Vorschlag 2 beschreibt dagegen die Verbindungsgerade selbst und $\rho_2 = 3$ ist eine Horizontale.
(2) Das Entscheidungsgebiet $I_1$ sollte natürlich den Punkt $s_1$ beinhalten ⇒ Gebiet unterhalb der Entscheidungsgeraden.
- Punkt $A = (1.5, \ \, 2)$ gehört zu diesem Entscheidungsgebiet, wie aus der Grafik hervorgeht.
- Rechnerisch lässt sich dies zeigen, da die Entscheidungsgerade zum Beispiel durch den Punkt $(1.5, \ \, 2.25)$ geht und somit $(1.5, \ \, 2)$ unterhalb der Entscheidungsgeraden liegt.
- Richtig ist also der Lösungsvorschlag 2.
(3) Die Entscheidungsgerade geht auch durch den Punkt $(3, \ \, 3.375)$.
- $B = (3, \ \, 3.5)$ liegt oberhalb und gehört somit zum Entscheidungsgebiet $I_0$ entsprechend dem Lösungsvorschlag 1.
(4) Entsprechend der Gleichung auf dem Angabenblatt und den Berechnungen zur Teilaufgabe (1) gilt nun:
- $$|| \boldsymbol{ s }_1||^2 - || \boldsymbol{ s }_0||^2 + 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
- Mit $|| \boldsymbol{ s }_1||^2 = 17$, $|| \boldsymbol{ s }_0||^2 = 26$, $ \boldsymbol{ s }_1 \, –\boldsymbol{ s }_0 = (3, \ \, –4)$ erhält man:
- $$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - K /8 \hspace{0.05cm}.$$
- Hierbei ist folgende Abkürzung verwendet worden:
- $$K = 2 \cdot \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_0)}{{\rm Pr}( m_1)} = 2 \cdot 1^2 \cdot 1.5 = 3 \hspace{0.05cm}.$$
- Daraus folgt weiter:
- $$\rho_2 = 3/4 \cdot \rho_1 + 9/8 - 3 /8 = 3/4 \cdot \rho_1 + 3/4 \hspace{0.05cm}.$$
- Die Entscheidungsgerade ist um $3/8$ nach unten verschoben $($schwarze Kurve, mit "$K = 3$" bezeichnet in der Grafik$)$.
- Richtig ist also der Lösungsvorschlag 2.
- Die erste Gleichung beschreibt die optimale Entscheidungsgrenze für gleichwahrscheinliche Symbole $(K = 0$, grau gestrichelt$)$.
- Die dritte Gleichung gilt für $K = \, –3$. Diese ergibt sich mit $\sigma_n^2 = 1$ für die Symbolwahrscheinlichkeiten ${\rm Pr}(m_1) \approx 0.817$, ${\rm Pr}(m_0) \approx 0.138$ $($grüne Kurve$)$.
- Die violette Gerade ergibt sich mit $K = 9$, also zum Beispiel bei gleichen Wahrscheinlichkeiten wie für die schwarze Kurve, aber nun mit der Varianz $\sigma_n^2 = 3$.
(5) Bereits aus obiger Grafik erkennt man, dass nun sowohl $A$ als auch $B$ zur Entscheidungsregion $I_0$ gehören. Richtig sind also die Lösungsvorschläge 1 und 3.