Aufgaben:Aufgabe 2.1: Zweidimensionale Impulsantwort: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
:$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$ | :$$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$ | ||
| − | gemäß der nebenstehenden Grafik analysiert werden. Die beiden Achsen sind zeitdiskret: | + | gemäß der nebenstehenden Grafik analysiert werden. Die beiden Achsen sind zeitdiskret: |
* $\tau$ kennzeichnet die <i>Verzögerungszeit</i> und kann im Beispiel Werte zwischen $0$ und $6 \ {\rm µ s}$ annehmen. | * $\tau$ kennzeichnet die <i>Verzögerungszeit</i> und kann im Beispiel Werte zwischen $0$ und $6 \ {\rm µ s}$ annehmen. | ||
| − | * Die ''absolute Zeit'' $t$ macht Aussagen über die Häufigkeit der Momentaufnahmen und charakterisiert die Zeitvarianz. Es gilt $t = n \cdot T$, wobei $T \gg \tau_{\rm max}$ gelten soll. | + | * Die ''absolute Zeit'' $t$ macht Aussagen über die Häufigkeit der Momentaufnahmen und charakterisiert die Zeitvarianz. Es gilt $t = n \cdot T$, wobei $T \gg \tau_{\rm max}$ gelten soll. |
| − | Die Pfeile in der Grafik markieren verschiedene Diracfunktionen mit den Impulsgewichten $1$ (rot), $1/2$ (blau) und $1/4$ (grün). Das bedeutet, dass hier auch die Verzögerungszeit $\tau$ zeitdiskret ist. | + | Die Pfeile in der Grafik markieren verschiedene Diracfunktionen mit den Impulsgewichten $1$ (rot), $1/2$ (blau) und $1/4$ (grün). Das bedeutet, dass hier auch die Verzögerungszeit $\tau$ zeitdiskret ist. |
| − | Bei den Messungen der Impulsantworten zu verschiedenen Zeiten $t$ im Sekundenabstand betrug die Auflösung der $\tau$–Achse $2$ Mikrosekunden $(\Delta \tau = 2 \ \rm µ s)$. Genauer wurden die Echos nicht lokalisiert. | + | Bei den Messungen der Impulsantworten zu verschiedenen Zeiten $t$ im Sekundenabstand betrug die Auflösung der $\tau$–Achse $2$ Mikrosekunden $(\Delta \tau = 2 \ \rm µ s)$. Genauer wurden die Echos nicht lokalisiert. |
Weiter wird in dieser Aufgabe noch auf folgende Größen Bezug genommen: | Weiter wird in dieser Aufgabe noch auf folgende Größen Bezug genommen: | ||
| − | * die < | + | * die <u>zeitvariante Übertragungsfunktion</u> entsprechend der Definition |
:$$H(f,\hspace{0.05cm} t) | :$$H(f,\hspace{0.05cm} t) | ||
| − | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0. | + | \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.1cm}t) |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * die Näherung der < | + | * die Näherung der <u>Kohärenzbandbreite</u> als Kehrwert der maximalen Ausdehnung von $h(\tau,\ t)$: |
:$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} | :$$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| Zeile 33: | Zeile 36: | ||
* Die Aufgabe gehört zum Themengebiet des Kapitels [[Mobile_Kommunikation/Allgemeine_Beschreibung_zeitvarianter_Systeme| Allgemeine Beschreibung zeitvarianter Systeme]]. | * Die Aufgabe gehört zum Themengebiet des Kapitels [[Mobile_Kommunikation/Allgemeine_Beschreibung_zeitvarianter_Systeme| Allgemeine Beschreibung zeitvarianter Systeme]]. | ||
* Genauere Informationen zu verschiedene Definitionen für die Kohärenzbandbreite finden Sie im Kapitel [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSSUS–Kanalmodell]], insbesondere in der Musterlösung zur [[Aufgaben:2.7_Koh%C3%A4renzbandbreite|Aufgabe 2.7Z]]. | * Genauere Informationen zu verschiedene Definitionen für die Kohärenzbandbreite finden Sie im Kapitel [[Mobile_Kommunikation/Das_GWSSUS%E2%80%93Kanalmodell| Das GWSSUS–Kanalmodell]], insbesondere in der Musterlösung zur [[Aufgaben:2.7_Koh%C3%A4renzbandbreite|Aufgabe 2.7Z]]. | ||
| − | * Anzumerken ist, dass es sich hier um eine konstruierte Aufgabe handelt. Entsprechend obiger Grafik ändert sich die 2D–Impulsantwort während der Zeitspanne $T$ gravierend. Deshalb ist $T$ hier als sehr groß zu interpretieren, zum Beispiel eine Stunde. | + | * Anzumerken ist, dass es sich hier um eine konstruierte Aufgabe handelt. Entsprechend obiger Grafik ändert sich die 2D–Impulsantwort während der Zeitspanne $T$ gravierend. Deshalb ist $T$ hier als sehr groß zu interpretieren, zum Beispiel eine Stunde. |
*Im Mobilfunk ändert sich $h(\tau, t)$ unter Berücksichtigung des Dopplereffektes im Millisekundenbereich, doch sind die Änderungen während dieser Zeit eher moderat. | *Im Mobilfunk ändert sich $h(\tau, t)$ unter Berücksichtigung des Dopplereffektes im Millisekundenbereich, doch sind die Änderungen während dieser Zeit eher moderat. | ||
| Zeile 41: | Zeile 44: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche Einschränkung bedeutet die Angabe $\Delta \tau = 2 \rm µ s$ für die maximale Bandbreite $B_{\rm max}$ des zu untersuchenden Nachrichtensignals? | + | {Welche Einschränkung bedeutet die Angabe $\Delta \tau = 2 \ \rm µ s$ für die maximale Bandbreite $B_{\rm max}$ des zu untersuchenden Nachrichtensignals? |
|type="{}"} | |type="{}"} | ||
$B_{\rm max} \ = \ ${ 500 3% } $\ \rm kHz$ | $B_{\rm max} \ = \ ${ 500 3% } $\ \rm kHz$ | ||
| − | {Zu welcher Zeit $t_2$ ist der Kanal ideal, gekennzeichnet durch $H(f, t_{\rm 2}) = 1$? | + | {Zu welcher Zeit $t_2$ ist der Kanal ideal, gekennzeichnet durch $H(f,\ t_{\rm 2}) = 1$? |
|type="{}"} | |type="{}"} | ||
$t_{\rm 2} \ = \ ${ 0. } $\ \cdot T$ | $t_{\rm 2} \ = \ ${ 0. } $\ \cdot T$ | ||
| Zeile 53: | Zeile 56: | ||
$t_{\rm 3} \ = \ ${ 3 3% } $\ \cdot T$ | $t_{\rm 3} \ = \ ${ 3 3% } $\ \cdot T$ | ||
| − | {Berechnen Sie die Kohärenzbandbreite für $t = 3T$, $t = 4T$ und $t = 5T$: | + | {Berechnen Sie die (näherungsweise) Kohärenzbandbreite für $t = 3T$, $t = 4T$ und $t = 5T$: |
|type="{}"} | |type="{}"} | ||
$t = 3T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \rm kHz$ | $t = 3T \text{:} \hspace{0.4cm} B_{\rm K} \hspace{0.01cm}' \ = \ ${ 250 3% } $\ \rm kHz$ | ||
| Zeile 64: | Zeile 67: | ||
{Für welchen der genannten $T$–Werte macht das Arbeiten mit der $\rm 2D$–Impulsantwort Sinn? | {Für welchen der genannten $T$–Werte macht das Arbeiten mit der $\rm 2D$–Impulsantwort Sinn? | ||
| − | |type=" | + | |type="()"} |
- Eine (langsame) Kanaländerung erfolgt etwa nach $T = 1 \ \rm µ s$. | - Eine (langsame) Kanaländerung erfolgt etwa nach $T = 1 \ \rm µ s$. | ||
+ Eine (langsame) Kanaländerung erfolgt etwa nach $T = 1 \ \rm s$. | + Eine (langsame) Kanaländerung erfolgt etwa nach $T = 1 \ \rm s$. | ||
| Zeile 71: | Zeile 74: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Das im äquivalenten Tiefpassbereich beschriebene Nachrichtensignal darf keine größere Bandbreite als $B_{\rm max} = 1/\Delta \tau \ \underline {= 500 \ \rm kHz}$ aufweisen. Diese mathematische (zweiseitige) Bandbreite des Tiefpass–Signals ist gleichzeitig die maximale physikalische (einseitige) Bandbreite des zugehörigen Bandpass–Signals. | + | '''(1)''' Das im äquivalenten Tiefpassbereich beschriebene Nachrichtensignal darf keine größere Bandbreite als $B_{\rm max} = 1/\Delta \tau \ \underline {= 500 \ \rm kHz}$ aufweisen. |
| + | *Diese mathematische (zweiseitige) Bandbreite des Tiefpass–Signals ist gleichzeitig die maximale physikalische (einseitige) Bandbreite des zugehörigen Bandpass–Signals. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' $H(f,\ t_{\rm 2}) = 1$ bedeutet im Zeitbereich $h(\tau,\ t_{\rm 2}) = \delta(\tau)$. | ||
| + | *Nur dann ist der Kanal ideal. | ||
| + | *Man erkennt aus der Grafik, dass dies nur für den Zeitpunkt $t_{\rm 2} \ \underline {= 0}$ zutrifft. | ||
| − | |||
| + | '''(3)''' Verzerrungen treten dann auf, wenn sich zum Zeitpunkt $t$ die Impulsantwort aus zwei oder mehr Diracfunktionen zusammensetzt ⇒ $t ≥ t_{\rm 3} \ \underline {= 3T}$. | ||
| + | *Zum Zeitpunkt $t = T$ wird das Signal $s(t)$ nur um $2 \ \rm µ s$ verzögert. | ||
| + | *Bei $t = 2T$ wird zusätzlich noch die Amplitude um $50 \%$ reduziert $(6 \ \rm dB$ Verlust$)$. | ||
| − | |||
| − | '''(4)''' Zum Zeitpunkt $t = 3T$ treten die beiden Diracfunktionen bei $\tau_{\rm min} = 0$ und $\tau_{\rm max} = 4 \ \rm | + | '''(4)''' Zum Zeitpunkt $t = 3T$ treten die beiden Diracfunktionen bei $\tau_{\rm min} = 0$ und $\tau_{\rm max} = 4 \ \rm µ s$ auf. |
| − | :$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\rm | + | *Die (einfache Näherung für die) Kohärenzbandbreite ist der Kehrwert hiervon: |
| + | :$$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\rm µ s} } \hspace{0.25cm} \underline{ = 250\,\,{\rm kHz}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Da auch zum Zeitpunkt $t = 4T$ die Diracfunktionen um $4 \ \rm | + | *Da auch zum Zeitpunkt $t = 4T$ die Diracfunktionen um $4 \ \rm µ s$ auseinanderliegen, erhält man hier ebenfalls $B_{\rm K} \hspace{0.01cm}' = \underline {250 \ \rm kHz}$. |
| − | *Bei $t = 5T$ hat die Impulsantwort eine Ausdehnung von $6 \ \rm | + | *Bei $t = 5T$ hat die Impulsantwort eine Ausdehnung von $6 \ \rm µ s \ \Rightarrow \ {\it B}_{\rm K} \hspace{0.01cm}' \ \underline {\approx 166.7 \ \rm kHz}$. |
| + | |||
| + | |||
| + | '''(5)''' Die Impulsantworten sind zu den Zeiten $5T$, $6T$ und $7T$ identisch und bestehen jeweils aus drei Diracs. | ||
| + | *Unter der Annahme, dass sich diesbezüglich auch für $t ≥ 8T$ nichts ändert, erhält man $t_{\rm 5} \ \underline {= 5T}$. | ||
| − | |||
'''(6)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | '''(6)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
| − | *Die zeitliche Veränderung der Impulsantwort, deren Dynamik durch den Parameter $T$ ausgedrückt wird, muss langsam sein im Vergleich zur maximalen Ausdehnung von $h(\tau, t)$, die in dieser Aufgabe gleich $\tau_{\rm max} = 6 \ \rm | + | *Die zeitliche Veränderung der Impulsantwort, deren Dynamik durch den Parameter $T$ ausgedrückt wird, muss langsam sein im Vergleich zur maximalen Ausdehnung von $h(\tau,\ t)$, die in dieser Aufgabe gleich $\tau_{\rm max} = 6 \ \rm µ s$ beträgt: |
| + | :$$T \gg \tau_{\rm max}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 13. Mai 2020, 16:33 Uhr
Es soll die zweidimensionale Impulsantwort
- $$h(\tau,\hspace{0.05cm}t) = \sum_{m = 1}^{M} z_m(t) \cdot {\rm \delta} (\tau - \tau_m)$$
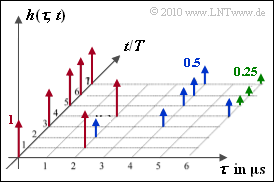
gemäß der nebenstehenden Grafik analysiert werden. Die beiden Achsen sind zeitdiskret:
- $\tau$ kennzeichnet die Verzögerungszeit und kann im Beispiel Werte zwischen $0$ und $6 \ {\rm µ s}$ annehmen.
- Die absolute Zeit $t$ macht Aussagen über die Häufigkeit der Momentaufnahmen und charakterisiert die Zeitvarianz. Es gilt $t = n \cdot T$, wobei $T \gg \tau_{\rm max}$ gelten soll.
Die Pfeile in der Grafik markieren verschiedene Diracfunktionen mit den Impulsgewichten $1$ (rot), $1/2$ (blau) und $1/4$ (grün). Das bedeutet, dass hier auch die Verzögerungszeit $\tau$ zeitdiskret ist.
Bei den Messungen der Impulsantworten zu verschiedenen Zeiten $t$ im Sekundenabstand betrug die Auflösung der $\tau$–Achse $2$ Mikrosekunden $(\Delta \tau = 2 \ \rm µ s)$. Genauer wurden die Echos nicht lokalisiert.
Weiter wird in dieser Aufgabe noch auf folgende Größen Bezug genommen:
- die zeitvariante Übertragungsfunktion entsprechend der Definition
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.1cm}t) \hspace{0.05cm},$$
- die Näherung der Kohärenzbandbreite als Kehrwert der maximalen Ausdehnung von $h(\tau,\ t)$:
- $$B_{\rm K} \hspace{0.01cm}' = \frac{1}{\tau_{\rm max} - \tau_{\rm min}} \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Themengebiet des Kapitels Allgemeine Beschreibung zeitvarianter Systeme.
- Genauere Informationen zu verschiedene Definitionen für die Kohärenzbandbreite finden Sie im Kapitel Das GWSSUS–Kanalmodell, insbesondere in der Musterlösung zur Aufgabe 2.7Z.
- Anzumerken ist, dass es sich hier um eine konstruierte Aufgabe handelt. Entsprechend obiger Grafik ändert sich die 2D–Impulsantwort während der Zeitspanne $T$ gravierend. Deshalb ist $T$ hier als sehr groß zu interpretieren, zum Beispiel eine Stunde.
- Im Mobilfunk ändert sich $h(\tau, t)$ unter Berücksichtigung des Dopplereffektes im Millisekundenbereich, doch sind die Änderungen während dieser Zeit eher moderat.
Fragebogen
Musterlösung
- Diese mathematische (zweiseitige) Bandbreite des Tiefpass–Signals ist gleichzeitig die maximale physikalische (einseitige) Bandbreite des zugehörigen Bandpass–Signals.
(2) $H(f,\ t_{\rm 2}) = 1$ bedeutet im Zeitbereich $h(\tau,\ t_{\rm 2}) = \delta(\tau)$.
- Nur dann ist der Kanal ideal.
- Man erkennt aus der Grafik, dass dies nur für den Zeitpunkt $t_{\rm 2} \ \underline {= 0}$ zutrifft.
(3) Verzerrungen treten dann auf, wenn sich zum Zeitpunkt $t$ die Impulsantwort aus zwei oder mehr Diracfunktionen zusammensetzt ⇒ $t ≥ t_{\rm 3} \ \underline {= 3T}$.
- Zum Zeitpunkt $t = T$ wird das Signal $s(t)$ nur um $2 \ \rm µ s$ verzögert.
- Bei $t = 2T$ wird zusätzlich noch die Amplitude um $50 \%$ reduziert $(6 \ \rm dB$ Verlust$)$.
(4) Zum Zeitpunkt $t = 3T$ treten die beiden Diracfunktionen bei $\tau_{\rm min} = 0$ und $\tau_{\rm max} = 4 \ \rm µ s$ auf.
- Die (einfache Näherung für die) Kohärenzbandbreite ist der Kehrwert hiervon:
- $$B_{\rm K}\hspace{0.01cm}' = \frac{1}{4\,\,{\rm µ s} } \hspace{0.25cm} \underline{ = 250\,\,{\rm kHz}} \hspace{0.05cm}.$$
- Da auch zum Zeitpunkt $t = 4T$ die Diracfunktionen um $4 \ \rm µ s$ auseinanderliegen, erhält man hier ebenfalls $B_{\rm K} \hspace{0.01cm}' = \underline {250 \ \rm kHz}$.
- Bei $t = 5T$ hat die Impulsantwort eine Ausdehnung von $6 \ \rm µ s \ \Rightarrow \ {\it B}_{\rm K} \hspace{0.01cm}' \ \underline {\approx 166.7 \ \rm kHz}$.
(5) Die Impulsantworten sind zu den Zeiten $5T$, $6T$ und $7T$ identisch und bestehen jeweils aus drei Diracs.
- Unter der Annahme, dass sich diesbezüglich auch für $t ≥ 8T$ nichts ändert, erhält man $t_{\rm 5} \ \underline {= 5T}$.
(6) Richtig ist der Lösungsvorschlag 2:
- Die zeitliche Veränderung der Impulsantwort, deren Dynamik durch den Parameter $T$ ausgedrückt wird, muss langsam sein im Vergleich zur maximalen Ausdehnung von $h(\tau,\ t)$, die in dieser Aufgabe gleich $\tau_{\rm max} = 6 \ \rm µ s$ beträgt:
- $$T \gg \tau_{\rm max}.$$