Applets:Huffman- und Shannon-Fano-Codierung: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{LntAppletLink|entropie}} ==Programmbeschreibung== <br> Dieses Applet soll den Begriff „Entropie” am Beispiel einer binären Nachrichtenquelle v…“) |
Höfler (Diskussion | Beiträge) K (Textersetzung - „Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29“ durch „Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_von_1974-2024.29“) |
||
| (20 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|shannon-huffman}} |
| + | |||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| − | Dieses Applet | + | Dieses Applet verdeutlicht die Quellencodierverfahren nach Huffman bzw. Shannon–Fano. Diese Verfahren komprimieren redundante wertdiskrete Quellen ohne Gedächtnis mit Stufenzahl $M$, dem Symbolvorrat $\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \} = \{ \rm A, \hspace{0.1cm} B, \hspace{0.1cm}\text{ ...}\}$ und den Symbolwahrscheinlichkeiten $p_{\rm A} \hspace{0.05cm},\hspace{0.1cm} p_{\rm B} \hspace{0.05cm}, \hspace{0.05cm}\text{ ...}$ . |
| − | + | Ziel der Quellencodierung und insbesondere der Klasse der Entropiecodierung – zu der „Huffman” und „Shannon–Fano” gehören – ist, dass die mittlere Codewortlänge $L_{\rm M}$ des binären Codes – darstellbar durch unterschiedlich lange Folgen von Nullen und Einsen – möglichst nahe an die Quellenentropie | |
| − | |||
| − | |||
| − | |||
| + | :$$H = \sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\mu})} = -\sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}{\rm Pr}(q_{\mu})\hspace{0.5cm}\big[\hspace{0.05cm}{\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Quellensymbol}\hspace{0.05cm}\big]$$ | ||
| − | + | heranreicht. Allgemein gilt $L_{\rm M} \ge H$, wobei das Gleichheitszeichen nicht für alle Symbolwahrscheinlichkeiten erreicht werden kann. | |
| − | |||
| − | |||
| − | + | Dargestellt werden jeweils | |
| + | * das Baumdiagramm zur Herleitung des jeweiligen Binärcodes, und | ||
| + | * eine simulierte Quellensymbolfolge der Länge $N = 10000$ (Entropie $H\hspace{0.05cm}' \approx H)$ und die dazugehörige Codesymbolfolge der Länge $L_{\rm M}\hspace{0.05cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} N$. | ||
| + | |||
| + | |||
| + | Auf die Einheiten „$\rm bit/Quellensymbol$” für die Entropie und die mittlere Codewortlänge wird im Programm verzichtet. | ||
| − | |||
| − | |||
| − | |||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | <br> | + | <br> |
| − | + | ===Der Huffman–Algorithmus=== | |
| + | Wir setzen voraus, dass die Quellensymbole $q_\nu$ einem Alphabet $\{q_μ\} = \{$ $\rm A$, $\rm B$ , $\rm C$ , ...$\}$ mit dem Symbolumfang $M$ entstammen und statistisch voneinander unabhängig seien. Beispielsweise gelte für den Symbolumfang $M = 8$: | ||
| + | |||
| + | :$$\{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm}, \boldsymbol{\rm B}\hspace{0.05cm}, \boldsymbol{\rm C}\hspace{0.05cm}, \boldsymbol{\rm D}\hspace{0.05cm}, \boldsymbol{\rm E}\hspace{0.05cm}, \boldsymbol{\rm F}\hspace{0.05cm}, \boldsymbol{\rm G}\hspace{0.05cm}, \boldsymbol{\rm H}\hspace{0.05cm} | ||
| + | \}\hspace{0.05cm}.$$ | ||
| − | + | [https://de.wikipedia.org/wiki/David_A._Huffman David A. Huffman] hat 1952 – also kurz nach Shannons bahnbrechenden Veröffentlichungen zur Informationstheorie – einen Algorithmus zur Konstruktion von optimalen präfixfreien Codes angegeben. | |
| + | Dieser ''Huffman–Algorithmus'' soll ohne Herleitung und Beweis angegeben werden, wobei wir uns hier auf Binärcodes beschränken. Das heißt: Für die Codesymbole gelte stets $c_ν ∈ \{$'''0''', '''1'''$\}$. Hier ist die Vorgehensweise: | ||
| − | |||
| − | |||
| − | + | # Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten. | |
| + | # Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen. | ||
| + | # Man wiederhole '''(1)''' und '''(2)''', bis nur mehr zwei (zusammengefasste) Symbole übrig bleiben. | ||
| + | # Man codiert die wahrscheinlichere Symbolmenge mit '''1''' und die andere Menge mit '''0'''. | ||
| + | # Man ergänzt in Gegenrichtung (also von unten nach oben) die jeweiligen Binärcodes der aufgespaltenen Teilmengen gemäß den Wahrscheinlichkeiten mit '''1''' bzw. '''0'''. | ||
| − | :$$ | + | |
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Ohne Einschränkung der Allgemeingültigkeit setzen wir voraus, dass die $M = 6$ Symbole $\rm A$, ... , $\rm F$ schon nach ihren Wahrscheinlichkeiten geordnet sind: | ||
| + | |||
| + | :$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Durch paarweises Zusammenfassen und anschießendem Sortieren erhält man in fünf Schritten die folgenden Symbolkombinationen <br>(resultierende Wahrscheinlichkeiten in Klammern): | |
| − | + | :1. $\rm A$ (0.30), $\rm B$ (0.24), $\rm C$ (0.20), $\rm EF$ (0.14), $\rm D$ (0.12), | |
| − | + | :2. $\rm A$ (0.30), $\rm EFD$ (0.26), $\rm B$ (0.24), $\rm C$ (0.20), | |
| − | + | :3. $\rm BC$ (0.44), $\rm A$ (0.30), $\rm EFD$ (0.26), | |
| − | + | :4. $\rm AEFD$ (0.56), $\rm BC$ (0.44), | |
| − | + | :5. Root $\rm AEFDBC$ (1.00). | |
| + | Rückwärts – alsogemäß den Schritten '''(5)''' bis '''(1)''' – erfolgt dann die Zuordnung zu Binärsymbolen. Ein '''x''' weist darauf hin, dass in den nächsten Schritten noch Bits hinzugefügt werden müssen: | ||
| + | :5. $\rm AEFD$ → '''1x''', $\rm BC$ → '''0x''', | ||
| + | :4. $\underline{\rm A}$ → '''<u>11</u>''', $\rm EFD$ → '''10x''', | ||
| + | :3. $\underline{\rm B}$ → '''<u>01</u>''', $\underline{\rm C}$ → '''<u>00</u>''', | ||
| + | :2. $\rm EF$ → '''101x''', $\underline{\rm D}$ → '''<u>100</u>''', | ||
| + | :1. $\underline{\rm E}$ → '''<u>1011</u>''', $\underline{\rm F}$ → '''<u>1010</u>'''. | ||
| + | Die Unterstreichungen markieren die endgültige Binärcodierung.}} | ||
| + | |||
| + | ===Zum Begriff „Entropiecodierung”=== | ||
| + | Wir gehen weiterhin von den Wahrscheinlichkeiten und Zuordnungen des letzten Beispiels aus: | ||
| + | |||
| + | :$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 | ||
| + | \hspace{0.05cm};$$ | ||
| − | + | :$$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} | |
| + | \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 01} \hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1011} \hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1010} \hspace{0.05cm}.$$ | ||
| − | + | Von den sechs Quellensymbolen werden also drei mit je zwei Bit, eines mit drei Bit und zwei Symbole $(\rm E$ und $\rm F)$ mit vier Bit codiert. | |
| − | |||
| − | Die | + | Die mittlere Codewortlänge ergibt sich damit zu |
| − | :$${\rm | + | :$$L_{\rm M} = (0.30 \hspace{-0.05cm}+ \hspace{-0.05cm}0.24 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.20) \cdot 2 + 0.12 \cdot 3 + (0.10 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.04 ) \cdot 4 = 2.4 \,{\rm bit/Quellensymbol} |
| − | + | \hspace{0.05cm}.$$ | |
| − | + | Aus dem Vergleich mit der Quellenentropie | |
| − | + | :$$H = -\big [0.3 \cdot {\rm log_2}\hspace{0.1cm}(0.3) + 0.24 \cdot {\rm log_2}\hspace{0.1cm}(0.24) | |
| − | :$$ | + | + 0.2 \cdot {\rm log_2}\hspace{0.1cm}(0.2)+ 0.12 \cdot {\rm log_2}\hspace{0.1cm}(0.12) |
| − | + | + 0.1 \cdot {\rm log_2}\hspace{0.1cm}(0.1)+ 0.04 \cdot {\rm log_2}\hspace{0.1cm}(0.04) | |
| − | + | \big ]= 2.365 \ \rm bit/Quellensymbol$$ | |
| − | + | erkennt man die Effizienz der Huffman–Codierung. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 2:}$ Wären die Symbolwahrscheinlichkeiten | ||
| − | :$$ | + | :$$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/4 \hspace{0.05cm},\hspace{0.2cm} |
| − | + | p_{\rm D} = 1/8 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = p_{\rm F} = 1/16 | |
| − | + | \hspace{0.05cm},$$ | |
| − | |||
| − | + | so würde für die Entropie und für die mittlere Codewortlänge gleichermaßen gelten: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | :$$ | + | :$$H = 3 \cdot 1/4 \cdot {\rm log_2}\hspace{0.1cm}(4) + 1/8 \cdot {\rm log_2}\hspace{0.1cm}(8) + 2 \cdot 1/16 \cdot {\rm log_2}\hspace{0.1cm}(16) = 2.375 \,{\rm bit/Quellensymbol}\hspace{0.05cm},$$ |
| − | + | :$$L_{\rm M} = 3 \cdot 1/4 \cdot 2 + 1/8 \cdot 3 + 2 \cdot 1/16 \cdot 4 = 2.375 \,{\rm bit/Quellensymbol} | |
| − | + | \hspace{0.05cm}.$$}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Aus dieser Eigenschaft $L_{\rm M} = H +\varepsilon$ mit $\varepsilon = 0$ bei geeigneten Auftrittswahrscheinlichkeiten erklärt sich der Begriff '''Entropiecodierung''': | ||
| − | + | ::Man versucht bei dieser Form von Quellencodierung, die Länge $L_μ$ der Binärfolge (bestehend aus Nullen und Einsen) für das Symbol $q_μ$ gemäß der Entropieberechnung wie folgt an dessen Auftrittswahrscheinlichkeit $p_μ$ anzupassen: | |
| − | |||
| − | |||
| − | |||
| − | :$$ | + | ::$$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$ |
| − | \hspace{0.05cm}.$$ | ||
| − | + | Da $L_μ$ im Gegensatz zu $\log_2(1/ p_μ$) ganzzahlig ist, gelingt dies nicht immer. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ mit $k = 1, 2, 3,$ ... dargestellt werden können. | |
| − | + | *In diesem Sonderfall – und nur in diesem – stimmt die mittlere Codewortlänge $L_{\rm M}$ exakt mit der Quellenentropie $H$ überein $(\varepsilon = 0$, siehe $\text{Beispiel 2}$). | |
| − | + | *Nach dem [[Informationstheorie/Allgemeine_Beschreibung#Quellencodierungstheorem|Quellencodierungstheorem]] gibt es keinen (decodierbaren) Code, der im Mittel mit weniger Binärzeichen pro Quellensymbol auskommt. | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Merke:}$ |
| − | + | Es gibt keinen präfixfreien (⇒ sofort decodierbaren) Code, der allein unter Ausnutzung der Auftrittswahrscheinlichkeiten zu einer kleineren mittleren Codewortlänge $L_{\rm M}$ führt als der Huffman–Code. '''In diesem Sinne ist der Huffman–Code optimal'''.}} | |
| − | + | ||
| − | + | ===Darstellung des Huffman–Codes als Baumdiagramm=== | |
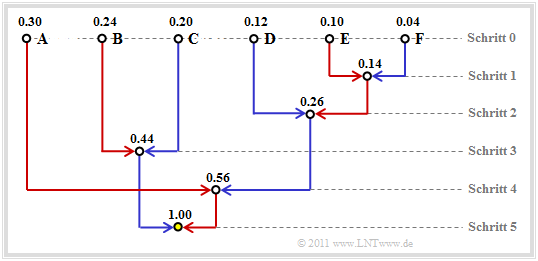
| − | + | Häufig wird zur Konstruktion des Huffman–Codes eine '''Baumstruktur''' verwendet. Für das bisher betrachtete Beispiel zeigt diese die folgende Grafik: | |
| − | |||
| + | [[Datei:P_ID2418__Inf_T_2_3_S3_neu.png|frame|Baumdarstellung der Huffman–Codierung für das $\text{Beispiel 1}$]] | ||
| − | + | Man erkennt: | |
| − | + | *Bei jedem Schritt des Huffman–Algorithmus werden die beiden Zweige mit den jeweils kleinsten Wahrscheinlichkeiten zusammengefasst. | |
| + | *Der Knoten im ersten Schritt fasst die zwei Symbole $\rm E$ und $\rm F$ mit den aktuell kleinsten Wahrscheinlichkeiten zusammen. Dieser Knoten ist mit $p_{\rm E} + p_{\rm F} = 0.14$ beschriftet. | ||
| + | *Der vom Symbol mit der kleineren Wahrscheinlichkeit $($hier $\rm F)$ zum Summenknoten verlaufende Zweig ist blau eingezeichnet, der andere Zweig $($für $\rm E)$ rot. | ||
| − | |||
| − | + | Nach fünf Schritten ist man bei der Baumwurzel („Root”) mit der Gesamtwahrscheinlichkeit $1.00$ angelangt. | |
| + | Verfolgt man nun den Verlauf von der Wurzel (in obiger Grafik mit gelber Füllung) zu den einzelnen Symbolen zurück, so kann man aus den Farben der einzelnen Zweige die Symbolzuordnung ablesen. Mit den Zuordnungen „rot” → '''1''' und „blau” → '''0''' ergibt sich beispielsweise von der Wurzel zu Symbol | ||
| + | * $\rm A$: rot, rot → '''11''', | ||
| + | *$\rm B$: blau, rot → '''01''', | ||
| + | *$\rm C$: blau, blau → '''00''', | ||
| + | *$\rm D$: rot, blau, blau → '''100''', | ||
| + | *$\rm E$: rot, blau, rot, rot → '''1011''', | ||
| + | *$\rm F$: rot, blau, rot, blau → '''1010'''. | ||
| + | Die (einheitliche) Zuordnung „rot” → '''0''' und „blau” → '''1''' würde ebenfalls zu einem optimalen präfixfreien Huffman–Code führen. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 3:}$ | ||
| + | Die folgende Grafik zeigt die Huffman–Codierung von $49$ Symbolen $q_ν ∈ \{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$, $\rm E$, $\rm F$ $\}$ mit der im letzten Abschnitt hergeleiteten Zuordnung. Die binäre Codesymbolfolge weist die mittlere Codewortlänge $L_{\rm M}\hspace{0.05cm}' = 125/49 = 2.551$ auf. Die Farben dienen ausschließlich zur besseren Orientierung. | ||
| + | [[Datei:Inf_T_2_3_S3b_version2.png|center|frame|Beispielfolgen bei Huffman–Codierung]] | ||
| + | Aufgrund der kurzen Quellensymbolfolge $(N = 49)$ weichen die Auftrittshäufigkeiten $h_{\rm A}$, ... , $h_{\rm F}$ der simulierten Folgen signifikant von den vorgegebenen Wahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm F}$ ab: | ||
| + | :$$p_{\rm A} = 0.30 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm A} = 16/49 \approx 0.326 \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm B} = 7/49 \approx 0.143 \hspace{0.05cm},$$ | ||
| + | |||
| + | :$$p_{\rm C} =0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm C}= 9/49 \approx 0.184 \hspace{0.05cm},\hspace{0.6cm}p_{\rm D} = 0.12 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm D} = 7/49 \approx 0.143 \hspace{0.05cm},$$ | ||
| − | === | + | :$$p_{\rm E}=0.10 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm},\hspace{0.6cm}p_{\rm F} = 0.04 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 |
| + | \hspace{0.05cm}.$$ | ||
| − | + | Damit ergibt sich ein etwas größerer Entropiewert: | |
| − | + | ||
| − | + | :$$H \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}p_{\mu}) = 2.365 \,{\rm bit/Quellensymbol}\hspace{0.3cm} | |
| − | + | \Rightarrow \hspace{0.3cm} | |
| − | + | H\hspace{0.05cm}' \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}h_{\mu}) = 2.451 \,{\rm bit/Quellensymbol} | |
| − | + | \hspace{0.05cm}.$$ | |
| − | |||
| − | + | Würde man den Huffman–Code mit diesen „neuen” Wahrscheinlichkeiten $h_{\rm A}$, ... , $h_{\rm F}$ bilden, so ergäben sich folgende Zuordnungen: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | :$ | + | : $\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''11'''$\hspace{0.05cm},\hspace{0.2cm} |
| − | + | \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''100'''$\hspace{0.05cm},\hspace{0.2cm} | |
| − | + | \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''00'''$\hspace{0.05cm},\hspace{0.2cm} | |
| + | \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''101'''$\hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''010'''$\hspace{0.05cm},\hspace{0.2cm} | ||
| + | \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$'''011'''$\hspace{0.05cm}.$ | ||
| − | + | Nun würden nur $\rm A$ und $\rm C$ mit zwei Bit dargestellt, die anderen vier Symbole durch jeweils drei Bit. | |
| − | + | *Die Codesymbolfolge hätte dann eine Länge von $(16 + 9) · 2 + (7 + 7 + 5 + 5) · 3 = 122$ Bit, wäre also um drei Bit kürzer als nach der bisherigen Codierung. | |
| − | + | *Die mittlere Codewortlänge wäre dann $L_{\rm M}\hspace{0.05cm}' = 122/49 ≈ 2.49 \ \rm bit/Quellensymbol$ anstelle von $L_{\rm M}\hspace{0.05cm}'≈ 2.55 \ \rm bit/Quellensymbol$.}} | |
| − | {{ | + | {{BlaueBox|TEXT= |
| − | $\text{ | + | $\text{Fazit:}$ |
| − | + | Dieses Beispiel lässt sich wie folgt interpretieren: | |
| − | * | + | *Die Huffman–Codierung lebt von der (genauen) Kenntnis der Symbolwahrscheinlichkeiten. Sind diese sowohl dem Sender als auch dem Empfänger bekannt, so ist die mittlere Codewortlänge $L_{\rm M}$ oft nur unwesentlich größer als die Quellenentropie $H$. |
| − | + | *Insbesondere aber bei kleinen Dateien kann es zu Abweichungen zwischen den (erwarteten) Symbolwahrscheinlichkeiten $p_μ$ und den (tatsächlichen) Häufigkeiten $h_μ$ kommen. Besser wäre es hier, für jede Datei einen eigenen Huffman–Code zu generieren, der auf den tatsächlichen Gegebenheiten $(h_μ)$ basiert. | |
| − | + | *In diesem Fall muss aber dem Decoder auch der spezifische Huffman–Code mitgeteilt werden. Dies führt zu einem gewissen Overhead, der nur wieder bei längeren Dateien vernachlässigt werden kann. Bei kleinen Dateien lohnt sich dieser Aufwand nicht.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | * | ||
| − | |||
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Der Shannon–Fano–Algorithmus === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 1949 – also bereits drei Jahre vor David A. Huffman – haben [https://de.wikipedia.org/wiki/Claude_Shannon Claude E. Shannon] und [https://de.wikipedia.org/wiki/Robert_Fano Robert Fano] einen ähnlichen, auf ''Entropiecodierung'' basierenden Algorithmus angegeben, nämlich: | |
| − | : | + | :# Man ordne die Quellensymbole nach fallenden Auftrittswahrscheinlichkeiten (identisch mit Huffman). |
| − | + | :# Man teile die sortierten Zeichen in zwei möglichst gleichwahrscheinliche Gruppen ein. | |
| + | :# Der ersten Gruppe wird das Binärsymbol '''1''' zugeordnet, der zweiten die '''0''' (oder umgekehrt). | ||
| + | :# Sind in einer Gruppe mehr als ein Zeichen, so ist auf diese der Algorithmus rekursiv anzuwenden. | ||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 4:}$ Wir gehen wie im [https://www.lntwww.de/Applets:Huffman-_und_Shannon-Fano-Codierung#Der_Huffman.E2.80.93Algorithmus Einführungsbeispiel] für den Huffman–Algorithmus von $M = 6$ Symbolen und den folgenden Wahrscheinlichkeiten aus: | ||
| − | :$$ | + | :$$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} |
| − | + | p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Dann lautet der Shannon–Fano–Algorithmus: | |
| + | :# $\rm AB$ → '''1'''x (Wahrscheinlichkeit 0.54), $\rm CDEF$ → '''0'''x (Wahrscheinlichkeit 0.46), | ||
| + | :# $\underline{\rm A}$ → '''<u>11</u>''' (Wahrscheinlichkeit 0.30), $\underline{\rm B}$ ⇒ '''<u>10</u>''' (Wahrscheinlichkeit 0.24), | ||
| + | :# $\underline{\rm C}$ → '''<u>01</u>''' (Wahrscheinlichkeit 0.20), $\rm DEF$ → '''00'''x, (Wahrscheinlichkeit 0.26), | ||
| + | :# $\underline{\rm D}$ → '''<u>001</u>''' (Wahrscheinlichkeit 0.12), $\rm EF$ → '''000'''x (Wahrscheinlichkeit 0.14), | ||
| + | :# $\underline{\rm E}$ → '''<u>0001</u>''' (Wahrscheinlichkeit 0.10), $\underline{\rm F}$ → '''<u>0000</u>''' (Wahrscheinlichkeit 0.04). | ||
| − | :$$ | + | ''Anmerkungen'': |
| + | *Ein „$\rm x$” weist wieder darauf hin, dass in nachfolgenden Codierschritten noch Bits hinzugefügt werden müssen. | ||
| + | *Es ergibt sich hier zwar eine andere Zuordnung als bei der [https://www.lntwww.de/Applets:Huffman-_und_Shannon-Fano-Codierung#Der_Huffman.E2.80.93Algorithmus Huffman–Codierung], aber genau die gleiche mittlere Codewortlänge: | ||
| + | |||
| + | :$$L_{\rm M} = (0.30\hspace{-0.05cm}+\hspace{-0.05cm} 0.24\hspace{-0.05cm}+ \hspace{-0.05cm}0.20) \hspace{-0.05cm}\cdot\hspace{-0.05cm} 2 + 0.12\hspace{-0.05cm} \cdot \hspace{-0.05cm} 3 + (0.10\hspace{-0.05cm}+\hspace{-0.05cm}0.04) \hspace{-0.05cm}\cdot \hspace{-0.05cm}4 = 2.4\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$}} | ||
| − | |||
| − | + | Mit den Wahrscheinlichkeiten entsprechend dem $\text{Beispiel 4}$ führt der Shannon–Fano–Algorithmus zur gleichen mittleren Codewortlänge wie die Huffman–Codierung. Ebenso sind bei vielen (eigentlich: den meisten) anderen Wahrscheinlichkeitsprofilen Huffman und Shannon–Fano aus informationstheoretischer Sicht äquivalent. | |
| − | + | Es gibt aber durchaus Fälle, bei denen sich beide Verfahren hinsichtlich der (mittleren) Codewortlänge unterscheiden, wie das folgende Beispiel zeigt. | |
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 2:}$ Wir betrachten $M = 5$ Symbole mit folgenden Wahrscheinlichkeiten: | ||
| + | |||
| + | :$$p_{\rm A} = 0.38 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.18 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm C}= 0.16 \hspace{0.05cm},\hspace{0.2cm} | ||
| + | p_{\rm D}= 0.15 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm E}= 0.13 \hspace{0.3cm} | ||
| + | \Rightarrow\hspace{0.3cm} H = 2.19\,{\rm bit/Quellensymbol} | ||
| + | \hspace{0.05cm}. $$ | ||
| − | : | + | [[Datei:P_ID2461__Inf_T_2_4_S1_ganz_neu.png|center|frame|Baumstrukturen nach Shannon–Fano bzw. Huffman]] |
| − | * | + | Die Grafik zeigt die jeweiligen Codebäume für Shannon–Fano (links) bzw. Huffman (rechts). Die Ergebnisse lassen sich wie folgt zusammenfassen: |
| + | * Der Shannon–Fano–Algorithmus führt zum Code $\rm A$ → '''11''', $\rm B$ → '''10''', $\rm C$ → '''01''', $\rm D$ → '''001''', $\rm E$ → '''000''' und damit zur mittleren Codewortlänge | ||
| + | |||
| + | :$$L_{\rm M} = (0.38 + 0.18 + 0.16) \cdot 2 + (0.15 + 0.13) \cdot 3 = 2.28\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$ | ||
| + | *Mit „Huffman” erhält man $\rm A$ → '''1''', $\rm B$ → '''001''', $\rm C$ → '''010''', $\rm D$ → '''001''', $\rm E$ → '''000''' und eine etwas kleinere mittlere Codewortlänge: | ||
| + | |||
| + | :$$L_{\rm M} = 0.38 \cdot 1 + (1-0.38) \cdot 3 = 2.24\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$ | ||
| − | + | *Es gibt keinen Satz von Wahrscheinlichkeiten, bei denen Shannon–Fano ein besseres Ergebnis liefert als der Huffman–Algorithmus, der stets den bestmöglichen Entropiecodierer bereitstellt. | |
| + | *Die Grafik zeigt zudem, dass die Algorithmen im Baumdiagramm in unterschiedlichen Richtungen vorgehen, nämlich einmal von der Wurzel zu den Einzelsymbolen (Shannon–Fano), zum anderen von den Einzelsymbolen zur Wurzel (Huffman).}} | ||
| − | |||
| − | |||
| − | + | ==Versuchsdurchführung== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:5.png|right]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[Datei: | ||
*Wählen Sie zunächst die Aufgabennummer. | *Wählen Sie zunächst die Aufgabennummer. | ||
*Eine Aufgabenbeschreibung wird angezeigt. | *Eine Aufgabenbeschreibung wird angezeigt. | ||
| − | *Alle | + | *Alle Parameter sind angepasst. |
| − | *Alle | + | *Alle Grafiken (Baumdiagramm, Symbolfolgen) sind aktualisiert. |
| + | *Ebenso die Ergebnisse $H, \ L_{\rm M}$ sowie $H\hspace{0.05cm}', \ L_{\rm M}\hspace{0.05cm}'$. | ||
*Musterlösung nach Drücken von „Hide solution”. | *Musterlösung nach Drücken von „Hide solution”. | ||
| − | * | + | *Nummer „0”: Gleiche Einstellung wie beim Programmstart. |
<br clear=all> | <br clear=all> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''(1)''' Wählen Sie die | + | '''(1)''' Wählen Sie die Quelle gemäß der Voreinstellung mit $M=8$ ⇒ Entropie $H=2.278$ (bit/Quellensymbol), Huffman-Codierung und „Herleitung”. |
| + | |||
| + | :Interpretieren Sie die Ergebnisse. Wie werden die Quellensymbole $\rm C$, $\rm D$ und $\rm E$ codiert? Wie groß ist die mittlere Codewortlänge $L_{\rm M}$? }} | ||
| − | : | + | ::* Es ergibt sich folgende Zuordnung: $\rm C \ \to 1$, $\rm D \ \to 01100$, $\rm E \ \to 0010$. Die mittlere Codewortlänge ist $L_{\rm M}= 2.29$ (bit/Quellensymbol) $>H$. |
| + | ::* Erklärung: Im Baumdiagramm kommt man von der „Root” (gelber Kreis) zum Symbol $\rm E$ über Blau – Blau – Rot – Blau. „Blau” steht für $0$ und „Rot” für $1$. | ||
| − | ::* | + | {{BlaueBox|TEXT= |
| − | ::* | + | '''(2)''' Wie unterscheiden sich bei sonst gleichen Einstellungen die Ergebnisse für „Shannon–Fano”? }} |
| + | |||
| + | ::* Hier ergibt sich eine andere Zuordnung: $\rm C \ \to 1$, $\rm D \ \to 01010$, $\rm E \ \to 0100$. Trotzdem ist die mittlere Codewortlänge wieder $L_{\rm M}= 2.29$. | ||
| + | ::* Erklärung: Im Graphen kommt man von der „Root” $\rm CAFBGEHD$ zu $\rm E$ über Blau – Rot – Blau – Blau. „Blau” steht wieder für $0$ und „Rot” für $1$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(3)''' Warum ist bei „Huffman” und „Shannon–Fano” trotz unterschiedlicher Zuordnung die mittlere Codewortlänge gleich?}} |
| − | ::* | + | ::* In beiden Fällen wird $\rm C$ mit einem Bit codiert, $\rm A$ und $\rm F$ mit drei Bit, $\rm B$, $\rm E$ und $\rm G$ mit vier Bit sowie $\rm D$ und $\rm H$ mit fünf Bit. Daraus folgt: |
| − | + | ::* $L_{\rm M}= p_{\rm C} \cdot 1 + \big [p_{\rm A} + p_{\rm F}\big] \cdot 3 + \big [p_{\rm B} + p_{\rm E}+ p_{\rm G}\big] \cdot 4 + \big [p_{\rm D} + p_{\rm H}\big] \cdot 5 = 0.52 \cdot 1 + 0.22 \cdot 3 + 0.19 \cdot 4 + 0.07 \cdot 5 = 2.29$ (bit/Quellensymbol) | |
| − | ::* | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(4)''' Wählen Sie „Voreinstellung” und „Huffman”. Wie ändern sich die Ergebnisse für „Simulation über 10000 Symbole” $(H', \ L_{\rm M}\hspace{0.05cm}')$ gegenüber $(H, \ L_{\rm M})$ für $N \to \infty$? |
| − | : | + | :Starten Sie jeweils zehn Simulationen. Welche Aussagen stimmen mit diesen Wahrscheinlichkeiten immer: $L_{\rm M}\hspace{0.05cm}' > L_{\rm M}$, $L_{\rm M}\hspace{0.05cm}' > H$, $L_{\rm M}\hspace{0.05cm}' > H'$?}} |
| − | ::* | + | ::* Für die theoretischen Werte (also für $N \to \infty)$ gilt immer $L_{\rm M} \ge H$. Außerdem wird für jede einzelne Simulation gelten: $L_{\rm M}\hspace{0.05cm}' \ge H'$. |
| − | + | ::* Da bei jeder einzelnen Simulation $H'$ größer, kleiner oder gleich $H$ sein kann, ist aber $L_{\rm M}\hspace{0.05cm}' < H$ durchaus möglich. | |
| − | ::* | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(5)''' Wählen Sie nun die „Quelle 3” $(M=4, \ p_{\rm A}= p_{\rm B}=p_{\rm C}= p_{\rm D}=0.25)$ und „Huffman”. Interpretieren Sie die Ergebnisse. Was wäre bei „Shannon–Fano”?}} |
| − | :: | + | ::* Jedes Symbol wird durch zwei Bit dargestellt, so dass $L_{\rm M} = H = 2$ (bit/Quellensymbol) ist. Die Simulation liefert auch immer $L_{\rm M}\hspace{0.05cm}' = 2$, auch für $H' < 2$. |
| − | :: | + | ::* Gleiches gilt für „Shannon–Fano” trotz anderer Zuordnung: $\rm A \ \to 00$, $\rm B \ \to 01$, $\rm C \ \to 10$, $\rm D \ \to 11$ statt $\rm A \ \to 01$, $\rm B \ \to 00$, $\rm C \ \to 11$, $\rm D \ \to 10$. |
| + | ::* Aber ganz klar ist: Quellencodierung macht bei redundanzfreier Quelle keinen Sinn, weder „Huffman” noch „Shannon–Fano”. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(6)''' Wählen Sie die „Quelle 4” $(M=4, \ p_{\rm A}= 0.5, \ p_{\rm B}= 0.25, \ p_{\rm C}= p_{\rm D}=0.125)$. Warum gilt hier $L_{\rm M} = H = 1.75$ (bit/Quellensymbol)? Interpretation. }} |
| − | ::* | + | ::* Sowohl bei „Huffman” als auch bei „Shannon–Fano” wird $\rm A$ mit einem Bit codiert, $\rm B$ mit zwei Bit sowie $\rm C$ und $\rm D$ mit drei Bit. |
| − | ::* | + | ::* Daraus folgt: $L_{\rm M}= 0.5 \cdot 1 + 0.25 \cdot 2 + 2 \cdot 0.125 \cdot 3 = H = 1.75$ (bit/Quellensymbol). Es sind „günstige Wahrscheinlichkeiten” der Form $p = 2^{-k}$. |
| + | ::* Ohne eine „Entropiecodierung” nach Huffman oder Shannon–Fano würden alle vier Symbole mit zwei Bit dargestellt: $L_{\rm M}= 2$ (bit/Quellensymbol). | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(7)''' Wählen Sie nun „Shannon–Fano” und die „Quelle 2” $(M=3, \ p_{\rm A}= 0.34, \ p_{\rm B}= p_{\rm C} =0.33)$. Mit welchen Wahrscheinlichkeiten ergäbe sich $L_{\rm M} = H $? }} |
| − | ::* | + | ::* Die Ternärquelle ist nahezu redundanzfrei: $H \approx \log_2 \ 3 \approx 1.585$. Mit $\rm A \ \to 0$, $\rm B \ \to 10$, $\rm C \ \to 11$ ist $L_{\rm M}= 1.66 > H$. |
| − | ::* | + | ::* „Günstige Wahrscheinlichkeiten” wären zum Beispiel $p_{\rm A}= 0.5, \ p_{\rm B}= p_{\rm C}= 0.25$ wie bei „Quelle 1”. Dann ist $L_{\rm M}= H = 1.5$ (bit/Quellensymbol). |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(8)''' Wählen Sie „Huffman” und die „Quelle 5” $(M=6, \ p_{\rm A}= p_{\rm B}= 0.25, \ p_{\rm C} = p_{\rm D} = p_{\rm E} = p_{\rm F} =0.125)$. Sind dies „günstige Wahrscheinlichkeiten”? }} |
| − | ::* | + | ::* $\rm JA$. Alle Wahrscheinlichkeiten sind $2^{-2}$ oder $2^{-3}$ ⇒ Symbole werden mit zwei oder drei Bit dargestellt ⇒ $L_{\rm M}= H = 2.5$ (bit/Quellensymbol). |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(9)''' Wie unterscheiden sich demgegenüber die Ergebnisse für „Quelle 6” $(M=6, \ p_{\rm A}= 0.26, \ p_{\rm B}= 0.24, \ p_{\rm C} = p_{\rm D} = 0.13, \ p_{\rm E} = p_{\rm F} =0.12)$? }} |
| − | ::* | + | ::* Bereits durch geringfügige Wahrscheinlichkeitsabweichungen ergeben sich ein anderer Baum und damit auch andere Symbolzuordnungen. |
| − | ::* | + | ::* $\rm A$ und $\rm B$ werden mit zwei Bit codiert, die anderen mit drei Bit. $L_{\rm M}= \big [p_{\rm A} + p_{\rm B}\big] \cdot 2 + \big [p_{\rm C} + p_{\rm D}+ p_{\E}+ p_{\F}\big] \cdot 3 = 2.5$ (bit/Quellensymbol). |
| − | + | ::* Die geänderten $p_{\rm A}$, ... verändern hier nicht die mittlere Codewortlänge, aber $H=2.499$ wird (geringfügig) kleiner ⇒ $L_{\rm M} > H$ (bit/Quellensymbol). | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(10)''' Betrachten Sie die „Quelle 9” $(M=8, \ p_{\rm A}= 0.8, \ p_{\rm B}= p_{\rm C}= p_{\rm D}=0.02, \ p_{\rm E} = 0.01$, ... , $p_{\rm H} = 0.01)$ ⇒ $H = 0.741$ (bit/Quellensymbol). Interpretation. }} |
| − | ::* | + | ::* Es ergibt sich mit $L_{\rm M} = 1.28$ ein sehr viel größerer Wert als $H = 0.741$ – sowohl für „Huffman” als auch für „Shannon–Fano”. |
| − | ::* | + | ::* Beide Verfahren sind also zur Quellenkomprimierung nicht geeignet, wenn eine Symbolwahrscheinlichkeit deutlich größer ist als 50%. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | '''( | + | '''(11)''' Die Komprimierung der „Quelle 9” $(M=8, H = 2.481)$ mit „Huffman” ergibt $L_{\rm M} = 2.58$. Welches Ergebnis liefert „Shannon–Fano”? Interpretation. }} |
| − | ::* | + | ::* Bei „Huffman” wird ein Symbol mit einem Bit codiert, zwei mit drei Bit, drei mit vier Bit und zwei mit fünf Bit ⇒ $L_{\rm M} = 2.58$ (bit/Quellensymbol). |
| − | ::* | + | ::* Entsprechend gilt für „Shannon–Fano”: zweimal zwei Bit, dreimal drei Bit, einmal vier Bit, zweimal fünf Bit ⇒ $L_{\rm M} = 2.61$ (bit/Quellensymbol). |
| + | ::* $\rm Fazit$: „Huffman” ist die optimale Entropiecodierung. „Shannon–Fano” erreicht meist das gleiche Ergebnis. $\text{Aber nicht immer!}$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ==Zur Handhabung des Applets== | ||
| + | [[Datei:Anleitung_Huffman_1.png|left|frame|Bildschirmabzug „Herleitung”]] | ||
| + | <br> | ||
| + | '''(A)''' Bildschirmauswahl: Herleitung / Simulation | ||
| − | + | '''(B)''' Auswahl zwischen 8 Nachrichtenquellen mit $M=3$ bis $M=8$ | |
| − | + | '''(C)''' Ausgewählte Wahrscheinlichkeiten | |
| − | + | '''(D)''' Entropie und mittlere Codewortlänge (Theorie, $N \to \infty$) | |
| − | |||
| − | '''( | ||
| − | '''( | + | '''(E)''' Auswahl des Kompressionsverfahrens: Huffman / Shannon-Fano |
| − | '''( | + | '''(F)''' Ergebnisse der Codewortzuweisung |
| − | '''( | + | '''(G)''' Entropie und mittlere Codewortlänge (Simulation über $N \to \infty$) |
| − | '''( | + | '''(H)''' Grafikfeld zur Herleitung des Codes gemäß Baumdiagramm |
| − | '''( | + | '''(I)''' Bereich für die Versuchsdurchführung: Aufgabenauswahl |
| − | '''( | + | '''(J)''' Bereich für die Versuchsdurchführung: Aufgabenstellung |
| − | '''( | + | '''(K)''' Bereich für die Versuchsdurchführung: Musterlösung |
| − | '''( | + | [[Datei:Anleitung_Huffman_2.png|right|frame|Bildschirmabzug „Simulation”]] |
| + | <br> <br> <br> <br> <br> <br> <br> | ||
| + | '''(L)''' Ausgabe der aktuellen Quellensymbolfolge | ||
| − | '''( | + | '''(M)''' Ausgabe der aktuellen Codesymbolfolge |
| − | '''( | + | '''(N)''' Neue Folgen simulieren |
| − | |||
<br clear=all> | <br clear=all> | ||
==Über die Autoren== | ==Über die Autoren== | ||
Dieses interaktive Applet wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Applet wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| − | *Die erste Version wurde 2011 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Eugen_Mehlmann_.28Bachelorarbeit_EI_2011.29|Eugen Mehlmann]] im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_. | + | *Die erste Version wurde 2011 von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Eugen_Mehlmann_.28Bachelorarbeit_EI_2011.29|Eugen Mehlmann]] im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_von_1974-2024.29|Günter Söder]]). |
| − | *2019 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Xiaohan_Liu_.28Bachelorarbeit_2018.29|Xiaohan Liu]] ( | + | *2019 wurde das Programm von [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_Studierende#Xiaohan_Liu_.28Bachelorarbeit_2018.2C_danach_Werkstudentin.29|Xiaohan Liu]] im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: [[Biografien_und_Bibliografien/An_LNTwww_beteiligte_LÜT-Angehörige#Dr.-Ing._Tasn.C3.A1d_Kernetzky_.28bei_L.C3.9CT_von_2014-2022.29|Tasnád Kernetzky]]). |
| + | |||
| + | |||
| + | Die Umsetzung dieses Applets auf HTML 5 wurde durch [https://www.ei.tum.de/studium/studienzuschuesse/ Studienzuschüsse] der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns. | ||
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|shannon-huffman}} |
Aktuelle Version vom 24. Februar 2025, 10:43 Uhr
Inhaltsverzeichnis
Programmbeschreibung
Dieses Applet verdeutlicht die Quellencodierverfahren nach Huffman bzw. Shannon–Fano. Diese Verfahren komprimieren redundante wertdiskrete Quellen ohne Gedächtnis mit Stufenzahl $M$, dem Symbolvorrat $\{ \hspace{0.05cm}q_{\mu}\hspace{0.01cm} \} = \{ \rm A, \hspace{0.1cm} B, \hspace{0.1cm}\text{ ...}\}$ und den Symbolwahrscheinlichkeiten $p_{\rm A} \hspace{0.05cm},\hspace{0.1cm} p_{\rm B} \hspace{0.05cm}, \hspace{0.05cm}\text{ ...}$ .
Ziel der Quellencodierung und insbesondere der Klasse der Entropiecodierung – zu der „Huffman” und „Shannon–Fano” gehören – ist, dass die mittlere Codewortlänge $L_{\rm M}$ des binären Codes – darstellbar durch unterschiedlich lange Folgen von Nullen und Einsen – möglichst nahe an die Quellenentropie
- $$H = \sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{{\rm Pr}(q_{\mu})} = -\sum_{\mu = 1}^{M} \hspace{0.2cm} {\rm Pr}(q_{\mu}) \cdot {\rm log_2}\hspace{0.1cm}{\rm Pr}(q_{\mu})\hspace{0.5cm}\big[\hspace{0.05cm}{\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Quellensymbol}\hspace{0.05cm}\big]$$
heranreicht. Allgemein gilt $L_{\rm M} \ge H$, wobei das Gleichheitszeichen nicht für alle Symbolwahrscheinlichkeiten erreicht werden kann.
Dargestellt werden jeweils
- das Baumdiagramm zur Herleitung des jeweiligen Binärcodes, und
- eine simulierte Quellensymbolfolge der Länge $N = 10000$ (Entropie $H\hspace{0.05cm}' \approx H)$ und die dazugehörige Codesymbolfolge der Länge $L_{\rm M}\hspace{0.05cm}' \hspace{-0.03cm}\cdot \hspace{-0.03cm} N$.
Auf die Einheiten „$\rm bit/Quellensymbol$” für die Entropie und die mittlere Codewortlänge wird im Programm verzichtet.
Theoretischer Hintergrund
Der Huffman–Algorithmus
Wir setzen voraus, dass die Quellensymbole $q_\nu$ einem Alphabet $\{q_μ\} = \{$ $\rm A$, $\rm B$ , $\rm C$ , ...$\}$ mit dem Symbolumfang $M$ entstammen und statistisch voneinander unabhängig seien. Beispielsweise gelte für den Symbolumfang $M = 8$:
- $$\{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm}, \boldsymbol{\rm B}\hspace{0.05cm}, \boldsymbol{\rm C}\hspace{0.05cm}, \boldsymbol{\rm D}\hspace{0.05cm}, \boldsymbol{\rm E}\hspace{0.05cm}, \boldsymbol{\rm F}\hspace{0.05cm}, \boldsymbol{\rm G}\hspace{0.05cm}, \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
David A. Huffman hat 1952 – also kurz nach Shannons bahnbrechenden Veröffentlichungen zur Informationstheorie – einen Algorithmus zur Konstruktion von optimalen präfixfreien Codes angegeben. Dieser Huffman–Algorithmus soll ohne Herleitung und Beweis angegeben werden, wobei wir uns hier auf Binärcodes beschränken. Das heißt: Für die Codesymbole gelte stets $c_ν ∈ \{$0, 1$\}$. Hier ist die Vorgehensweise:
- Man ordne die Symbole nach fallenden Auftrittswahrscheinlichkeiten.
- Man fasse die zwei unwahrscheinlichsten Symbole zu einem neuen Symbol zusammen.
- Man wiederhole (1) und (2), bis nur mehr zwei (zusammengefasste) Symbole übrig bleiben.
- Man codiert die wahrscheinlichere Symbolmenge mit 1 und die andere Menge mit 0.
- Man ergänzt in Gegenrichtung (also von unten nach oben) die jeweiligen Binärcodes der aufgespaltenen Teilmengen gemäß den Wahrscheinlichkeiten mit 1 bzw. 0.
$\text{Beispiel 1:}$ Ohne Einschränkung der Allgemeingültigkeit setzen wir voraus, dass die $M = 6$ Symbole $\rm A$, ... , $\rm F$ schon nach ihren Wahrscheinlichkeiten geordnet sind:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Durch paarweises Zusammenfassen und anschießendem Sortieren erhält man in fünf Schritten die folgenden Symbolkombinationen
(resultierende Wahrscheinlichkeiten in Klammern):
- 1. $\rm A$ (0.30), $\rm B$ (0.24), $\rm C$ (0.20), $\rm EF$ (0.14), $\rm D$ (0.12),
- 2. $\rm A$ (0.30), $\rm EFD$ (0.26), $\rm B$ (0.24), $\rm C$ (0.20),
- 3. $\rm BC$ (0.44), $\rm A$ (0.30), $\rm EFD$ (0.26),
- 4. $\rm AEFD$ (0.56), $\rm BC$ (0.44),
- 5. Root $\rm AEFDBC$ (1.00).
Rückwärts – alsogemäß den Schritten (5) bis (1) – erfolgt dann die Zuordnung zu Binärsymbolen. Ein x weist darauf hin, dass in den nächsten Schritten noch Bits hinzugefügt werden müssen:
- 5. $\rm AEFD$ → 1x, $\rm BC$ → 0x,
- 4. $\underline{\rm A}$ → 11, $\rm EFD$ → 10x,
- 3. $\underline{\rm B}$ → 01, $\underline{\rm C}$ → 00,
- 2. $\rm EF$ → 101x, $\underline{\rm D}$ → 100,
- 1. $\underline{\rm E}$ → 1011, $\underline{\rm F}$ → 1010.
Die Unterstreichungen markieren die endgültige Binärcodierung.
Zum Begriff „Entropiecodierung”
Wir gehen weiterhin von den Wahrscheinlichkeiten und Zuordnungen des letzten Beispiels aus:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm};$$
- $$\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 11} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 01} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 00} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 100} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1011} \hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm} \boldsymbol{\rm 1010} \hspace{0.05cm}.$$
Von den sechs Quellensymbolen werden also drei mit je zwei Bit, eines mit drei Bit und zwei Symbole $(\rm E$ und $\rm F)$ mit vier Bit codiert.
Die mittlere Codewortlänge ergibt sich damit zu
- $$L_{\rm M} = (0.30 \hspace{-0.05cm}+ \hspace{-0.05cm}0.24 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.20) \cdot 2 + 0.12 \cdot 3 + (0.10 \hspace{-0.05cm}+ \hspace{-0.05cm} 0.04 ) \cdot 4 = 2.4 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Aus dem Vergleich mit der Quellenentropie
- $$H = -\big [0.3 \cdot {\rm log_2}\hspace{0.1cm}(0.3) + 0.24 \cdot {\rm log_2}\hspace{0.1cm}(0.24) + 0.2 \cdot {\rm log_2}\hspace{0.1cm}(0.2)+ 0.12 \cdot {\rm log_2}\hspace{0.1cm}(0.12) + 0.1 \cdot {\rm log_2}\hspace{0.1cm}(0.1)+ 0.04 \cdot {\rm log_2}\hspace{0.1cm}(0.04) \big ]= 2.365 \ \rm bit/Quellensymbol$$
erkennt man die Effizienz der Huffman–Codierung.
$\text{Beispiel 2:}$ Wären die Symbolwahrscheinlichkeiten
- $$p_{\rm A} = p_{\rm B} = p_{\rm C} = 1/4 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 1/8 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = p_{\rm F} = 1/16 \hspace{0.05cm},$$
so würde für die Entropie und für die mittlere Codewortlänge gleichermaßen gelten:
- $$H = 3 \cdot 1/4 \cdot {\rm log_2}\hspace{0.1cm}(4) + 1/8 \cdot {\rm log_2}\hspace{0.1cm}(8) + 2 \cdot 1/16 \cdot {\rm log_2}\hspace{0.1cm}(16) = 2.375 \,{\rm bit/Quellensymbol}\hspace{0.05cm},$$
- $$L_{\rm M} = 3 \cdot 1/4 \cdot 2 + 1/8 \cdot 3 + 2 \cdot 1/16 \cdot 4 = 2.375 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Aus dieser Eigenschaft $L_{\rm M} = H +\varepsilon$ mit $\varepsilon = 0$ bei geeigneten Auftrittswahrscheinlichkeiten erklärt sich der Begriff Entropiecodierung:
- Man versucht bei dieser Form von Quellencodierung, die Länge $L_μ$ der Binärfolge (bestehend aus Nullen und Einsen) für das Symbol $q_μ$ gemäß der Entropieberechnung wie folgt an dessen Auftrittswahrscheinlichkeit $p_μ$ anzupassen:
- $$L_{\mu} = {\rm log}_2\hspace{0.1cm}(1/p_{\mu} ) \hspace{0.05cm}.$$
Da $L_μ$ im Gegensatz zu $\log_2(1/ p_μ$) ganzzahlig ist, gelingt dies nicht immer.
Natürlich gelingt das nicht immer, sondern nur dann, wenn alle Auftrittswahrscheinlichkeiten $p_μ$ in der Form $2^{–k}$ mit $k = 1, 2, 3,$ ... dargestellt werden können.
- In diesem Sonderfall – und nur in diesem – stimmt die mittlere Codewortlänge $L_{\rm M}$ exakt mit der Quellenentropie $H$ überein $(\varepsilon = 0$, siehe $\text{Beispiel 2}$).
- Nach dem Quellencodierungstheorem gibt es keinen (decodierbaren) Code, der im Mittel mit weniger Binärzeichen pro Quellensymbol auskommt.
$\text{Merke:}$ Es gibt keinen präfixfreien (⇒ sofort decodierbaren) Code, der allein unter Ausnutzung der Auftrittswahrscheinlichkeiten zu einer kleineren mittleren Codewortlänge $L_{\rm M}$ führt als der Huffman–Code. In diesem Sinne ist der Huffman–Code optimal.
Darstellung des Huffman–Codes als Baumdiagramm
Häufig wird zur Konstruktion des Huffman–Codes eine Baumstruktur verwendet. Für das bisher betrachtete Beispiel zeigt diese die folgende Grafik:
Man erkennt:
- Bei jedem Schritt des Huffman–Algorithmus werden die beiden Zweige mit den jeweils kleinsten Wahrscheinlichkeiten zusammengefasst.
- Der Knoten im ersten Schritt fasst die zwei Symbole $\rm E$ und $\rm F$ mit den aktuell kleinsten Wahrscheinlichkeiten zusammen. Dieser Knoten ist mit $p_{\rm E} + p_{\rm F} = 0.14$ beschriftet.
- Der vom Symbol mit der kleineren Wahrscheinlichkeit $($hier $\rm F)$ zum Summenknoten verlaufende Zweig ist blau eingezeichnet, der andere Zweig $($für $\rm E)$ rot.
Nach fünf Schritten ist man bei der Baumwurzel („Root”) mit der Gesamtwahrscheinlichkeit $1.00$ angelangt.
Verfolgt man nun den Verlauf von der Wurzel (in obiger Grafik mit gelber Füllung) zu den einzelnen Symbolen zurück, so kann man aus den Farben der einzelnen Zweige die Symbolzuordnung ablesen. Mit den Zuordnungen „rot” → 1 und „blau” → 0 ergibt sich beispielsweise von der Wurzel zu Symbol
- $\rm A$: rot, rot → 11,
- $\rm B$: blau, rot → 01,
- $\rm C$: blau, blau → 00,
- $\rm D$: rot, blau, blau → 100,
- $\rm E$: rot, blau, rot, rot → 1011,
- $\rm F$: rot, blau, rot, blau → 1010.
Die (einheitliche) Zuordnung „rot” → 0 und „blau” → 1 würde ebenfalls zu einem optimalen präfixfreien Huffman–Code führen.
$\text{Beispiel 3:}$ Die folgende Grafik zeigt die Huffman–Codierung von $49$ Symbolen $q_ν ∈ \{$ $\rm A$, $\rm B$, $\rm C$, $\rm D$, $\rm E$, $\rm F$ $\}$ mit der im letzten Abschnitt hergeleiteten Zuordnung. Die binäre Codesymbolfolge weist die mittlere Codewortlänge $L_{\rm M}\hspace{0.05cm}' = 125/49 = 2.551$ auf. Die Farben dienen ausschließlich zur besseren Orientierung.
Aufgrund der kurzen Quellensymbolfolge $(N = 49)$ weichen die Auftrittshäufigkeiten $h_{\rm A}$, ... , $h_{\rm F}$ der simulierten Folgen signifikant von den vorgegebenen Wahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm F}$ ab:
- $$p_{\rm A} = 0.30 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm A} = 16/49 \approx 0.326 \hspace{0.05cm},\hspace{0.4cm}p_{\rm B} = 0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm B} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm C} =0.24 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm C}= 9/49 \approx 0.184 \hspace{0.05cm},\hspace{0.6cm}p_{\rm D} = 0.12 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm D} = 7/49 \approx 0.143 \hspace{0.05cm},$$
- $$p_{\rm E}=0.10 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm},\hspace{0.6cm}p_{\rm F} = 0.04 \hspace{0.05cm} \Rightarrow \hspace{0.05cm} h_{\rm E} = 5/49 \approx 0.102 \hspace{0.05cm}.$$
Damit ergibt sich ein etwas größerer Entropiewert:
- $$H \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}p_{\mu}) = 2.365 \,{\rm bit/Quellensymbol}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H\hspace{0.05cm}' \ ({\rm bez\ddot{u}glich }\hspace{0.15cm}h_{\mu}) = 2.451 \,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Würde man den Huffman–Code mit diesen „neuen” Wahrscheinlichkeiten $h_{\rm A}$, ... , $h_{\rm F}$ bilden, so ergäben sich folgende Zuordnungen:
- $\boldsymbol{\rm A} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$11$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm B} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$100$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm C} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$00$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm D} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$101$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm E} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$010$\hspace{0.05cm},\hspace{0.2cm} \boldsymbol{\rm F} \hspace{0.05cm} \rightarrow \hspace{0.05cm}$011$\hspace{0.05cm}.$
Nun würden nur $\rm A$ und $\rm C$ mit zwei Bit dargestellt, die anderen vier Symbole durch jeweils drei Bit.
- Die Codesymbolfolge hätte dann eine Länge von $(16 + 9) · 2 + (7 + 7 + 5 + 5) · 3 = 122$ Bit, wäre also um drei Bit kürzer als nach der bisherigen Codierung.
- Die mittlere Codewortlänge wäre dann $L_{\rm M}\hspace{0.05cm}' = 122/49 ≈ 2.49 \ \rm bit/Quellensymbol$ anstelle von $L_{\rm M}\hspace{0.05cm}'≈ 2.55 \ \rm bit/Quellensymbol$.
$\text{Fazit:}$ Dieses Beispiel lässt sich wie folgt interpretieren:
- Die Huffman–Codierung lebt von der (genauen) Kenntnis der Symbolwahrscheinlichkeiten. Sind diese sowohl dem Sender als auch dem Empfänger bekannt, so ist die mittlere Codewortlänge $L_{\rm M}$ oft nur unwesentlich größer als die Quellenentropie $H$.
- Insbesondere aber bei kleinen Dateien kann es zu Abweichungen zwischen den (erwarteten) Symbolwahrscheinlichkeiten $p_μ$ und den (tatsächlichen) Häufigkeiten $h_μ$ kommen. Besser wäre es hier, für jede Datei einen eigenen Huffman–Code zu generieren, der auf den tatsächlichen Gegebenheiten $(h_μ)$ basiert.
- In diesem Fall muss aber dem Decoder auch der spezifische Huffman–Code mitgeteilt werden. Dies führt zu einem gewissen Overhead, der nur wieder bei längeren Dateien vernachlässigt werden kann. Bei kleinen Dateien lohnt sich dieser Aufwand nicht.
Der Shannon–Fano–Algorithmus
1949 – also bereits drei Jahre vor David A. Huffman – haben Claude E. Shannon und Robert Fano einen ähnlichen, auf Entropiecodierung basierenden Algorithmus angegeben, nämlich:
- Man ordne die Quellensymbole nach fallenden Auftrittswahrscheinlichkeiten (identisch mit Huffman).
- Man teile die sortierten Zeichen in zwei möglichst gleichwahrscheinliche Gruppen ein.
- Der ersten Gruppe wird das Binärsymbol 1 zugeordnet, der zweiten die 0 (oder umgekehrt).
- Sind in einer Gruppe mehr als ein Zeichen, so ist auf diese der Algorithmus rekursiv anzuwenden.
$\text{Beispiel 4:}$ Wir gehen wie im Einführungsbeispiel für den Huffman–Algorithmus von $M = 6$ Symbolen und den folgenden Wahrscheinlichkeiten aus:
- $$p_{\rm A} = 0.30 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.24 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.20 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.12 \hspace{0.05cm},\hspace{0.2cm}p_{\rm E} = 0.10 \hspace{0.05cm},\hspace{0.2cm}p_{\rm F} = 0.04 \hspace{0.05cm}.$$
Dann lautet der Shannon–Fano–Algorithmus:
- $\rm AB$ → 1x (Wahrscheinlichkeit 0.54), $\rm CDEF$ → 0x (Wahrscheinlichkeit 0.46),
- $\underline{\rm A}$ → 11 (Wahrscheinlichkeit 0.30), $\underline{\rm B}$ ⇒ 10 (Wahrscheinlichkeit 0.24),
- $\underline{\rm C}$ → 01 (Wahrscheinlichkeit 0.20), $\rm DEF$ → 00x, (Wahrscheinlichkeit 0.26),
- $\underline{\rm D}$ → 001 (Wahrscheinlichkeit 0.12), $\rm EF$ → 000x (Wahrscheinlichkeit 0.14),
- $\underline{\rm E}$ → 0001 (Wahrscheinlichkeit 0.10), $\underline{\rm F}$ → 0000 (Wahrscheinlichkeit 0.04).
Anmerkungen:
- Ein „$\rm x$” weist wieder darauf hin, dass in nachfolgenden Codierschritten noch Bits hinzugefügt werden müssen.
- Es ergibt sich hier zwar eine andere Zuordnung als bei der Huffman–Codierung, aber genau die gleiche mittlere Codewortlänge:
- $$L_{\rm M} = (0.30\hspace{-0.05cm}+\hspace{-0.05cm} 0.24\hspace{-0.05cm}+ \hspace{-0.05cm}0.20) \hspace{-0.05cm}\cdot\hspace{-0.05cm} 2 + 0.12\hspace{-0.05cm} \cdot \hspace{-0.05cm} 3 + (0.10\hspace{-0.05cm}+\hspace{-0.05cm}0.04) \hspace{-0.05cm}\cdot \hspace{-0.05cm}4 = 2.4\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
Mit den Wahrscheinlichkeiten entsprechend dem $\text{Beispiel 4}$ führt der Shannon–Fano–Algorithmus zur gleichen mittleren Codewortlänge wie die Huffman–Codierung. Ebenso sind bei vielen (eigentlich: den meisten) anderen Wahrscheinlichkeitsprofilen Huffman und Shannon–Fano aus informationstheoretischer Sicht äquivalent.
Es gibt aber durchaus Fälle, bei denen sich beide Verfahren hinsichtlich der (mittleren) Codewortlänge unterscheiden, wie das folgende Beispiel zeigt.
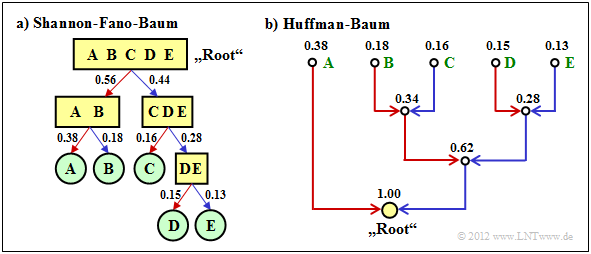
$\text{Beispiel 2:}$ Wir betrachten $M = 5$ Symbole mit folgenden Wahrscheinlichkeiten:
- $$p_{\rm A} = 0.38 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm B}= 0.18 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm C}= 0.16 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D}= 0.15 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm E}= 0.13 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H = 2.19\,{\rm bit/Quellensymbol} \hspace{0.05cm}. $$
Die Grafik zeigt die jeweiligen Codebäume für Shannon–Fano (links) bzw. Huffman (rechts). Die Ergebnisse lassen sich wie folgt zusammenfassen:
- Der Shannon–Fano–Algorithmus führt zum Code $\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 001, $\rm E$ → 000 und damit zur mittleren Codewortlänge
- $$L_{\rm M} = (0.38 + 0.18 + 0.16) \cdot 2 + (0.15 + 0.13) \cdot 3 = 2.28\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Mit „Huffman” erhält man $\rm A$ → 1, $\rm B$ → 001, $\rm C$ → 010, $\rm D$ → 001, $\rm E$ → 000 und eine etwas kleinere mittlere Codewortlänge:
- $$L_{\rm M} = 0.38 \cdot 1 + (1-0.38) \cdot 3 = 2.24\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$
- Es gibt keinen Satz von Wahrscheinlichkeiten, bei denen Shannon–Fano ein besseres Ergebnis liefert als der Huffman–Algorithmus, der stets den bestmöglichen Entropiecodierer bereitstellt.
- Die Grafik zeigt zudem, dass die Algorithmen im Baumdiagramm in unterschiedlichen Richtungen vorgehen, nämlich einmal von der Wurzel zu den Einzelsymbolen (Shannon–Fano), zum anderen von den Einzelsymbolen zur Wurzel (Huffman).
Versuchsdurchführung
- Wählen Sie zunächst die Aufgabennummer.
- Eine Aufgabenbeschreibung wird angezeigt.
- Alle Parameter sind angepasst.
- Alle Grafiken (Baumdiagramm, Symbolfolgen) sind aktualisiert.
- Ebenso die Ergebnisse $H, \ L_{\rm M}$ sowie $H\hspace{0.05cm}', \ L_{\rm M}\hspace{0.05cm}'$.
- Musterlösung nach Drücken von „Hide solution”.
- Nummer „0”: Gleiche Einstellung wie beim Programmstart.
(1) Wählen Sie die Quelle gemäß der Voreinstellung mit $M=8$ ⇒ Entropie $H=2.278$ (bit/Quellensymbol), Huffman-Codierung und „Herleitung”.
- Interpretieren Sie die Ergebnisse. Wie werden die Quellensymbole $\rm C$, $\rm D$ und $\rm E$ codiert? Wie groß ist die mittlere Codewortlänge $L_{\rm M}$?
- Es ergibt sich folgende Zuordnung: $\rm C \ \to 1$, $\rm D \ \to 01100$, $\rm E \ \to 0010$. Die mittlere Codewortlänge ist $L_{\rm M}= 2.29$ (bit/Quellensymbol) $>H$.
- Erklärung: Im Baumdiagramm kommt man von der „Root” (gelber Kreis) zum Symbol $\rm E$ über Blau – Blau – Rot – Blau. „Blau” steht für $0$ und „Rot” für $1$.
(2) Wie unterscheiden sich bei sonst gleichen Einstellungen die Ergebnisse für „Shannon–Fano”?
- Hier ergibt sich eine andere Zuordnung: $\rm C \ \to 1$, $\rm D \ \to 01010$, $\rm E \ \to 0100$. Trotzdem ist die mittlere Codewortlänge wieder $L_{\rm M}= 2.29$.
- Erklärung: Im Graphen kommt man von der „Root” $\rm CAFBGEHD$ zu $\rm E$ über Blau – Rot – Blau – Blau. „Blau” steht wieder für $0$ und „Rot” für $1$.
(3) Warum ist bei „Huffman” und „Shannon–Fano” trotz unterschiedlicher Zuordnung die mittlere Codewortlänge gleich?
- In beiden Fällen wird $\rm C$ mit einem Bit codiert, $\rm A$ und $\rm F$ mit drei Bit, $\rm B$, $\rm E$ und $\rm G$ mit vier Bit sowie $\rm D$ und $\rm H$ mit fünf Bit. Daraus folgt:
- $L_{\rm M}= p_{\rm C} \cdot 1 + \big [p_{\rm A} + p_{\rm F}\big] \cdot 3 + \big [p_{\rm B} + p_{\rm E}+ p_{\rm G}\big] \cdot 4 + \big [p_{\rm D} + p_{\rm H}\big] \cdot 5 = 0.52 \cdot 1 + 0.22 \cdot 3 + 0.19 \cdot 4 + 0.07 \cdot 5 = 2.29$ (bit/Quellensymbol)
(4) Wählen Sie „Voreinstellung” und „Huffman”. Wie ändern sich die Ergebnisse für „Simulation über 10000 Symbole” $(H', \ L_{\rm M}\hspace{0.05cm}')$ gegenüber $(H, \ L_{\rm M})$ für $N \to \infty$?
- Starten Sie jeweils zehn Simulationen. Welche Aussagen stimmen mit diesen Wahrscheinlichkeiten immer: $L_{\rm M}\hspace{0.05cm}' > L_{\rm M}$, $L_{\rm M}\hspace{0.05cm}' > H$, $L_{\rm M}\hspace{0.05cm}' > H'$?
- Für die theoretischen Werte (also für $N \to \infty)$ gilt immer $L_{\rm M} \ge H$. Außerdem wird für jede einzelne Simulation gelten: $L_{\rm M}\hspace{0.05cm}' \ge H'$.
- Da bei jeder einzelnen Simulation $H'$ größer, kleiner oder gleich $H$ sein kann, ist aber $L_{\rm M}\hspace{0.05cm}' < H$ durchaus möglich.
(5) Wählen Sie nun die „Quelle 3” $(M=4, \ p_{\rm A}= p_{\rm B}=p_{\rm C}= p_{\rm D}=0.25)$ und „Huffman”. Interpretieren Sie die Ergebnisse. Was wäre bei „Shannon–Fano”?
- Jedes Symbol wird durch zwei Bit dargestellt, so dass $L_{\rm M} = H = 2$ (bit/Quellensymbol) ist. Die Simulation liefert auch immer $L_{\rm M}\hspace{0.05cm}' = 2$, auch für $H' < 2$.
- Gleiches gilt für „Shannon–Fano” trotz anderer Zuordnung: $\rm A \ \to 00$, $\rm B \ \to 01$, $\rm C \ \to 10$, $\rm D \ \to 11$ statt $\rm A \ \to 01$, $\rm B \ \to 00$, $\rm C \ \to 11$, $\rm D \ \to 10$.
- Aber ganz klar ist: Quellencodierung macht bei redundanzfreier Quelle keinen Sinn, weder „Huffman” noch „Shannon–Fano”.
(6) Wählen Sie die „Quelle 4” $(M=4, \ p_{\rm A}= 0.5, \ p_{\rm B}= 0.25, \ p_{\rm C}= p_{\rm D}=0.125)$. Warum gilt hier $L_{\rm M} = H = 1.75$ (bit/Quellensymbol)? Interpretation.
- Sowohl bei „Huffman” als auch bei „Shannon–Fano” wird $\rm A$ mit einem Bit codiert, $\rm B$ mit zwei Bit sowie $\rm C$ und $\rm D$ mit drei Bit.
- Daraus folgt: $L_{\rm M}= 0.5 \cdot 1 + 0.25 \cdot 2 + 2 \cdot 0.125 \cdot 3 = H = 1.75$ (bit/Quellensymbol). Es sind „günstige Wahrscheinlichkeiten” der Form $p = 2^{-k}$.
- Ohne eine „Entropiecodierung” nach Huffman oder Shannon–Fano würden alle vier Symbole mit zwei Bit dargestellt: $L_{\rm M}= 2$ (bit/Quellensymbol).
(7) Wählen Sie nun „Shannon–Fano” und die „Quelle 2” $(M=3, \ p_{\rm A}= 0.34, \ p_{\rm B}= p_{\rm C} =0.33)$. Mit welchen Wahrscheinlichkeiten ergäbe sich $L_{\rm M} = H $?
- Die Ternärquelle ist nahezu redundanzfrei: $H \approx \log_2 \ 3 \approx 1.585$. Mit $\rm A \ \to 0$, $\rm B \ \to 10$, $\rm C \ \to 11$ ist $L_{\rm M}= 1.66 > H$.
- „Günstige Wahrscheinlichkeiten” wären zum Beispiel $p_{\rm A}= 0.5, \ p_{\rm B}= p_{\rm C}= 0.25$ wie bei „Quelle 1”. Dann ist $L_{\rm M}= H = 1.5$ (bit/Quellensymbol).
(8) Wählen Sie „Huffman” und die „Quelle 5” $(M=6, \ p_{\rm A}= p_{\rm B}= 0.25, \ p_{\rm C} = p_{\rm D} = p_{\rm E} = p_{\rm F} =0.125)$. Sind dies „günstige Wahrscheinlichkeiten”?
- $\rm JA$. Alle Wahrscheinlichkeiten sind $2^{-2}$ oder $2^{-3}$ ⇒ Symbole werden mit zwei oder drei Bit dargestellt ⇒ $L_{\rm M}= H = 2.5$ (bit/Quellensymbol).
(9) Wie unterscheiden sich demgegenüber die Ergebnisse für „Quelle 6” $(M=6, \ p_{\rm A}= 0.26, \ p_{\rm B}= 0.24, \ p_{\rm C} = p_{\rm D} = 0.13, \ p_{\rm E} = p_{\rm F} =0.12)$?
- Bereits durch geringfügige Wahrscheinlichkeitsabweichungen ergeben sich ein anderer Baum und damit auch andere Symbolzuordnungen.
- $\rm A$ und $\rm B$ werden mit zwei Bit codiert, die anderen mit drei Bit. $L_{\rm M}= \big [p_{\rm A} + p_{\rm B}\big] \cdot 2 + \big [p_{\rm C} + p_{\rm D}+ p_{\E}+ p_{\F}\big] \cdot 3 = 2.5$ (bit/Quellensymbol).
- Die geänderten $p_{\rm A}$, ... verändern hier nicht die mittlere Codewortlänge, aber $H=2.499$ wird (geringfügig) kleiner ⇒ $L_{\rm M} > H$ (bit/Quellensymbol).
(10) Betrachten Sie die „Quelle 9” $(M=8, \ p_{\rm A}= 0.8, \ p_{\rm B}= p_{\rm C}= p_{\rm D}=0.02, \ p_{\rm E} = 0.01$, ... , $p_{\rm H} = 0.01)$ ⇒ $H = 0.741$ (bit/Quellensymbol). Interpretation.
- Es ergibt sich mit $L_{\rm M} = 1.28$ ein sehr viel größerer Wert als $H = 0.741$ – sowohl für „Huffman” als auch für „Shannon–Fano”.
- Beide Verfahren sind also zur Quellenkomprimierung nicht geeignet, wenn eine Symbolwahrscheinlichkeit deutlich größer ist als 50%.
(11) Die Komprimierung der „Quelle 9” $(M=8, H = 2.481)$ mit „Huffman” ergibt $L_{\rm M} = 2.58$. Welches Ergebnis liefert „Shannon–Fano”? Interpretation.
- Bei „Huffman” wird ein Symbol mit einem Bit codiert, zwei mit drei Bit, drei mit vier Bit und zwei mit fünf Bit ⇒ $L_{\rm M} = 2.58$ (bit/Quellensymbol).
- Entsprechend gilt für „Shannon–Fano”: zweimal zwei Bit, dreimal drei Bit, einmal vier Bit, zweimal fünf Bit ⇒ $L_{\rm M} = 2.61$ (bit/Quellensymbol).
- $\rm Fazit$: „Huffman” ist die optimale Entropiecodierung. „Shannon–Fano” erreicht meist das gleiche Ergebnis. $\text{Aber nicht immer!}$
Zur Handhabung des Applets
(A) Bildschirmauswahl: Herleitung / Simulation
(B) Auswahl zwischen 8 Nachrichtenquellen mit $M=3$ bis $M=8$
(C) Ausgewählte Wahrscheinlichkeiten
(D) Entropie und mittlere Codewortlänge (Theorie, $N \to \infty$)
(E) Auswahl des Kompressionsverfahrens: Huffman / Shannon-Fano
(F) Ergebnisse der Codewortzuweisung
(G) Entropie und mittlere Codewortlänge (Simulation über $N \to \infty$)
(H) Grafikfeld zur Herleitung des Codes gemäß Baumdiagramm
(I) Bereich für die Versuchsdurchführung: Aufgabenauswahl
(J) Bereich für die Versuchsdurchführung: Aufgabenstellung
(K) Bereich für die Versuchsdurchführung: Musterlösung
(L) Ausgabe der aktuellen Quellensymbolfolge
(M) Ausgabe der aktuellen Codesymbolfolge
(N) Neue Folgen simulieren
Über die Autoren
Dieses interaktive Applet wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2011 von Eugen Mehlmann im Rahmen seiner Bachelorarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2019 wurde das Programm von Xiaohan Liu im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).
Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.