Aufgaben:Aufgabe 1.14: Bhattacharyya–Schranke für BEC: Unterschied zwischen den Versionen
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
:$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$ | :$$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$ | ||
| − | Am Ausgang des digitalen Kanals, der durch das [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|BEC–Modell]] ( | + | Am Ausgang des digitalen Kanals, der durch das [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Binary_Erasure_Channel_.E2.80.93_BEC|"BEC–Modell"]] ("Binary Erasure Channel") mit der Auslöschungswahrscheinlichkeit $\lambda = 0.001$ festgelegt wird, tritt der Empfangsvektor |
:$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$ | :$$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$ | ||
| − | auf, wobei für $i = 1, \ \text{...} \ , 5$ gilt: $y_{i} \in \{0, 1, \rm E\}$ | + | auf, wobei für $i = 1, \ \text{...} \ , 5$ gilt: |
| + | :$$y_{i} \in \{0, 1, \rm E\}.$$ | ||
| − | Der BEC–Kanal zeichnet sich dadurch aus, dass | + | Der BEC–Kanal zeichnet sich dadurch aus, dass |
| − | *Verfälschungen $(0 → 1, 1 → 0)$ ausgeschlossen sind, | + | *Verfälschungen $(0 → 1,\ 1 → 0)$ ausgeschlossen sind, |
| − | |||
| + | *es aber zu Auslöschungen $(0 → \rm E,\ 1 → E)$ kommen kann. | ||
| − | Die Grafik zeigt explizit alle möglichen Empfangsvektoren $\underline{y}$ mit drei oder mehr Auslöschungen $($englisch: | + | |
| + | Die Grafik zeigt explizit alle möglichen Empfangsvektoren $\underline{y}$ mit drei oder mehr Auslöschungen $($englisch: "Erasures", abgekürzt $\rm E)$ unter der Voraussetzung, dass der Nullvektor $(0, 0, 0, 0, 0)$ gesendet wurde. | ||
| + | |||
*Bei weniger als drei Auslöschungen liefert bei dem betrachteten $(5, 2)$–Code der Codewortfinder immer die richtige Entscheidung: $\underline{z} = \underline{x}$. | *Bei weniger als drei Auslöschungen liefert bei dem betrachteten $(5, 2)$–Code der Codewortfinder immer die richtige Entscheidung: $\underline{z} = \underline{x}$. | ||
| − | *Bei drei oder mehr Auslöschungen kann es dagegen zu Fehlentscheidungen kommen. In diesem Fall gilt für die Blockfehlerwahrscheinlichkeit: | + | *Bei drei oder mehr Auslöschungen kann es dagegen zu Fehlentscheidungen kommen. In diesem Fall gilt für die Blockfehlerwahrscheinlichkeit: |
:$$ {\rm Pr(Blockfehler)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$ | :$$ {\rm Pr(Blockfehler)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$ | ||
| Zeile 36: | Zeile 39: | ||
Bitte beachten Sie: | Bitte beachten Sie: | ||
| − | *Das Ereignis $[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht unbedingt aus, dass beim betrachteten Empfangsvektor $\underline{y}$ tatsächlich für das Codewort $\underline{x}_{1}$ entschieden wird, sondern lediglich, dass die Entscheidung für $x_{1}$ aufgrund der Statistik sinnvoller wäre als die Entscheidung für $\underline{x}_{0}$. | + | *Das Ereignis $[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht unbedingt aus, dass beim betrachteten Empfangsvektor $\underline{y}$ tatsächlich für das Codewort $\underline{x}_{1}$ entschieden wird, sondern lediglich, dass die Entscheidung für $x_{1}$ aufgrund der Statistik sinnvoller wäre als die Entscheidung für $\underline{x}_{0}$. |
| − | *Es könnte aber auch für $\underline{x}_{2}$ oder $\underline{x}_{3}$ entschieden werden, wenn das [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Maximum-a-posteriori.E2.80.93_und_Maximum-Likelihood.E2.80.93Kriterium|Maximum–Likelihood–Kriterium]] hierfür spricht. | + | |
| + | *Es könnte aber auch für $\underline{x}_{2}$ oder $\underline{x}_{3}$ entschieden werden, wenn das [[Kanalcodierung/Kanalmodelle_und_Entscheiderstrukturen#Maximum-a-posteriori.E2.80.93_und_Maximum-Likelihood.E2.80.93Kriterium|"Maximum–Likelihood–Kriterium"]] hierfür spricht. | ||
| − | Die Berechnung der Blockfehlerwahrscheinlichkeit ist schwierig, da die Ereignisse $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ und $[\underline{x}_{0} → \underline{x}_{3}]$ nicht notwendigerweise [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Disjunkte_Mengen|disjunkt]] sind. Eine obere Schranke liefert die [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit|Union Bound]]: | + | Die Berechnung der Blockfehlerwahrscheinlichkeit ist schwierig, da die Ereignisse $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ und $[\underline{x}_{0} → \underline{x}_{3}]$ nicht notwendigerweise [[Stochastische_Signaltheorie/Mengentheoretische_Grundlagen#Disjunkte_Mengen|disjunkt]] sind. Eine obere Schranke liefert die [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Union_Bound_der_Blockfehlerwahrscheinlichkeit|"Union Bound"]]: |
:$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$ | :$${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$ | ||
| Zeile 48: | Zeile 52: | ||
:$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(Blockfehler)} \hspace{0.05cm},$$ | :$${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(Blockfehler)} \hspace{0.05cm},$$ | ||
| − | wobei beim Binary Erasure Channel für den Bhattacharyya–Parameter $\beta = \lambda$ gilt und $W(X)$ die [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Distanzspektrum_eines_linearen_Codes|Gewichtsfunktion]] angibt, wobei die Pseudo–Variable $X$ hier durch den Bhattacharyya–Parameter $\lambda$ zu ersetzen ist. | + | wobei beim Binary Erasure Channel $\rm (BEC)$ für den Bhattacharyya–Parameter $\beta = \lambda$ gilt und $W(X)$ die [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit#Distanzspektrum_eines_linearen_Codes|Gewichtsfunktion]] angibt, wobei die Pseudo–Variable $X$ hier durch den Bhattacharyya–Parameter $\lambda$ zu ersetzen ist. |
| − | *Die Bhattacharyya–Schranke liegt je nach Kanal mehr oder weniger weit oberhalb der | + | *Die Bhattacharyya–Schranke liegt je nach Kanal mehr oder weniger weit oberhalb der "Union Bound". |
| − | *Ihre Bedeutung liegt darin, dass die Schranke für unterschiedliche Kanäle in gleicher Weise angebbar ist. | + | |
| + | *Ihre Bedeutung liegt darin, dass die Schranke für unterschiedliche Kanäle in gleicher Weise angebbar ist. | ||
| Zeile 57: | Zeile 62: | ||
| − | + | Hinweis: Die Aufgabe gehört zum Kapitel [[Kanalcodierung/Schranken_für_die_Blockfehlerwahrscheinlichkeit|"Schranken für die Blockfehlerwahrscheinlichkeit"]]. | |
| − | |||
| − | |||
| − | |||
| Zeile 67: | Zeile 69: | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die paarweise Fehlerwahrscheinlichkeit zwischen den Codeworten $\underline{x}_{0} = (0, 0, 0, 0, 0)$ und $\underline{x}_{1} = (0, 1, 0, 1, 1)$? | + | {Wie groß ist die paarweise Fehlerwahrscheinlichkeit zwischen den Codeworten $\underline{x}_{0} = (0, 0, 0, 0, 0)$ und $\underline{x}_{1} = (0, 1, 0, 1, 1)$? |
|type="{}"} | |type="{}"} | ||
${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}] \ = \ $ { 0.5 3% }$\ \cdot 10^{-3} $ | ||
| − | {Welche Aussagen stimmen bezüglich ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ mit Laufindex $i = 1, \ \text{...} \ , 3$? | + | {Welche Aussagen stimmen bezüglich ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ mit Laufindex $i = 1, \ \text{...} \ , 3$? $d_{{\rm H},\hspace{0.05cm}i}$ bezeichnet hier die Hamming–Distanz zwischen $x_{0}$ und $x_{i}$. |
|type="()"} | |type="()"} | ||
- Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$. | - Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ \lambda ^{d_{{\rm H},\hspace{0.05cm}i}} \ · \ (1 – \lambda)^{n \hspace{0.05cm}– \hspace{0.05cm}d_{{\rm H},\hspace{0.05cm}i}}$. | ||
+ Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$ | + Es gilt ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}] \ = \ 1/2 · \lambda ^{d_{{\rm H},\hspace{0.05cm}i}}.$ | ||
| − | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ ist die Verfälschungswahrscheinlichkeit von $x_{0}$ nach $x_{i}$. | + | - ${\rm Pr}[\underline{x}_{0} → \underline{x}_{i}]$ ist die Verfälschungswahrscheinlichkeit von $x_{0}$ nach $x_{i}$. |
{Wie groß sind die folgenden Wahrscheinlichkeiten? | {Wie groß sind die folgenden Wahrscheinlichkeiten? | ||
| Zeile 83: | Zeile 85: | ||
$\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr}[\underline{x}_{0} → \underline{x}_{3}] \ = \ $ { 0.05 3% } $\ \cdot 10^{-3} $ | ||
| − | {Geben Sie die | + | {Geben Sie die "Union Bound" für die Blockfehlerwahrscheinlichkeit an. |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Union\ Bound)} \ = \ ${ 1.05 3% } $\ \cdot 10^{-3} $ | ||
| − | {Wie lautet im vorliegenden Fall die | + | {Wie lautet im vorliegenden Fall die "Bhattacharyya–Schranke"? |
|type="{}"} | |type="{}"} | ||
$\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | $\ {\rm Pr(Bhattacharyya)} \ = \ ${ 2.1 3% } $\ \cdot 10^{-3} $ | ||
| Zeile 95: | Zeile 97: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Die Codeworte $\underline{x}_{0}$ und $\underline{x}_{1}$ unterscheiden sich in Bit $2, \ 4$ und $5$. Wird nur einer dieser drei Binärwerte richtig übertragen, ist damit das gesamte Codewort eindeutig bestimmt. Keine Information über das Codewort erhält man bei folgenden Empfangsvektoren (siehe Tabelle auf der Angabenseite): | + | '''(1)''' Die Codeworte $\underline{x}_{0}$ und $\underline{x}_{1}$ unterscheiden sich in Bit $2, \ 4$ und $5$. Wird nur einer dieser drei Binärwerte richtig übertragen, ist damit das gesamte Codewort eindeutig bestimmt. Keine Information über das Codewort erhält man bei folgenden Empfangsvektoren (siehe Tabelle auf der Angabenseite): |
| − | * $\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^3 \ · \ (1 – \lambda)^2$, | + | * $\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^3 \ · \ (1 – \lambda)^2$, |
| − | * $\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$, | + | * $\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$, |
| − | * $\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$, | + | * $\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$, |
| − | * $\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^5$. | + | * $\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^5$. |
| − | Die Wahrscheinlichkeit, dass aufgrund des spezifischen Empfangsvektors $\underline{y}$ das Codewort $\underline{x}_{1}$ genau so wahrscheinlich ist wie $\underline{x}_{0}$, ergibt sich zu | + | Die Wahrscheinlichkeit, dass aufgrund des spezifischen Empfangsvektors $\underline{y}$ das Codewort $\underline{x}_{1}$ genau so wahrscheinlich ist wie $\underline{x}_{0}$, ergibt sich zu |
:$$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm und}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm sind \hspace{0.15cm}gleichwahrscheinlich}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$ | :$$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm und}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm sind \hspace{0.15cm}gleichwahrscheinlich}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$ | ||
| − | In diesem Fall entscheidet man sich nach dem Zufallsprinzip | + | In diesem Fall entscheidet man sich nach dem Zufallsprinzip für $\underline{x}_{0}$ (wäre richtig) oder für $\underline{x}_{1}$ (leider falsch), und zwar mit gleicher Wahrscheinlichkeit. Daraus folgt: |
:$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$ | :$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' Nach Teilaufgabe '''(1)''' ist die <u>Antwort 2</u> richtig und nicht die Antwort 1. Auch die Aussage 3 ist falsch: | ||
| + | *${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht aus, dass mit dieser Wahrscheinlickeit das Codewort $\underline{x}_{0}$ tatsächlich in das falsche Codewort $\underline{x}_{1}$ übergeht, sondern nur, dass es mit dieser Wahrscheinlichkeit zu $\underline{x}_{1}$ übergehen könnte. | ||
| + | |||
| + | * ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ beinhaltet auch Konstellationen, bei denen die Entscheidung tatsächlich für $\underline{x}_{2}$ bzw. $\underline{x}_{3}$ fällt. | ||
| − | '''(3)''' Wegen $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ und $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ ergibt sich hierfür | + | |
| + | |||
| + | '''(3)''' Wegen $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ und $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ ergibt sich hierfür | ||
| − | :$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}, | + | :$${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm},$$ |
| + | :$$ {\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = 1/2 \cdot \lambda^4 \hspace{0.15cm} \underline{= 0.05 \cdot 10^{-3}} \hspace{0.05cm}.$$ | ||
| − | '''(4)''' Die Blockfehlerwahrscheinlichkeit ist nie größer (mit einer gewissen Wahrscheinlichkeit eher kleiner) als die so genannte | + | |
| + | '''(4)''' Die Blockfehlerwahrscheinlichkeit ist nie größer (mit einer gewissen Wahrscheinlichkeit eher kleiner) als die so genannte "Union Bound": | ||
:$${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$ | :$${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$ | ||
| + | |||
| Zeile 130: | Zeile 138: | ||
:$${\rm Pr(Blockfehler) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$ | :$${\rm Pr(Blockfehler) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$ | ||
| − | Für das Distanzspektrum bzw. die Gewichtsfunktion erhält man im vorliegenden Fall: | + | *Für das Distanzspektrum bzw. die Gewichtsfunktion erhält man im vorliegenden Fall: |
:$$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$ | :$$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$ | ||
| − | Beim BEC–Kanal gilt zudem $\beta = \lambda$. Daraus folgt als Endergebnis für $\lambda = 0.001$: | + | *Beim BEC–Kanal gilt zudem $\beta = \lambda$. Daraus folgt als Endergebnis für $\lambda = 0.001$: |
:$${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$ | :$${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$ | ||
| − | Anzumerken ist, dass beim BEC–Modell die | + | *Anzumerken ist, dass beim BEC–Modell die "Bhattacharyya–Schranke" stets doppelt so groß ist wie die "Union Bound", die ja selbst wieder eine obere Schranke für die Blockfehlerwahrscheinlichkeit darstellt. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 4. August 2022, 16:14 Uhr
Wir betrachten in dieser Aufgabe den systematischen $(5, 2)$–Code
- mit der $2×5$–Generatormatrix
- $${ \boldsymbol{\rm G}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &1 &0\\ 0 &1 &0 &1 &1 \end{pmatrix} \hspace{0.05cm},$$
- der $3 × 5$–Prüfmatrix
- $${ \boldsymbol{\rm H}}_{(5, 2)} = \begin{pmatrix} 1 &0 &1 &0 &0\\ 1 &1 &0 &1 &0\\ 0 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},$$
- und den $2^k = 4$ Codeworten
- $$\underline{x}_0 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_1 = (0, 1, 0, 1, 1)\hspace{0.05cm},\hspace{0.2cm}\underline{x}_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} (1, 0, 1, 1, 0) \hspace{0.05cm},\hspace{0.2cm}\underline{x}_3 = (1, 1, 1, 0, 1)\hspace{0.05cm}.$$
Am Ausgang des digitalen Kanals, der durch das "BEC–Modell" ("Binary Erasure Channel") mit der Auslöschungswahrscheinlichkeit $\lambda = 0.001$ festgelegt wird, tritt der Empfangsvektor
- $$\underline{y} = (y_1, \hspace{0.05cm}y_2, \hspace{0.05cm}y_3, \hspace{0.05cm}y_4, \hspace{0.05cm}y_5)$$
auf, wobei für $i = 1, \ \text{...} \ , 5$ gilt:
- $$y_{i} \in \{0, 1, \rm E\}.$$
Der BEC–Kanal zeichnet sich dadurch aus, dass
- Verfälschungen $(0 → 1,\ 1 → 0)$ ausgeschlossen sind,
- es aber zu Auslöschungen $(0 → \rm E,\ 1 → E)$ kommen kann.
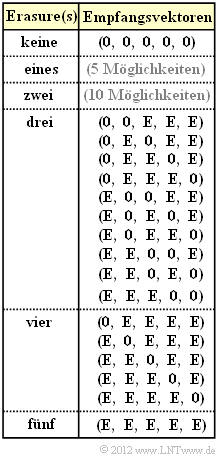
Die Grafik zeigt explizit alle möglichen Empfangsvektoren $\underline{y}$ mit drei oder mehr Auslöschungen $($englisch: "Erasures", abgekürzt $\rm E)$ unter der Voraussetzung, dass der Nullvektor $(0, 0, 0, 0, 0)$ gesendet wurde.
- Bei weniger als drei Auslöschungen liefert bei dem betrachteten $(5, 2)$–Code der Codewortfinder immer die richtige Entscheidung: $\underline{z} = \underline{x}$.
- Bei drei oder mehr Auslöschungen kann es dagegen zu Fehlentscheidungen kommen. In diesem Fall gilt für die Blockfehlerwahrscheinlichkeit:
- $$ {\rm Pr(Blockfehler)}= {\rm Pr} (\underline{z} \ne \underline{x}) = {\rm Pr}\left \{ \hspace{0.1cm} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] \hspace{0.05cm}\cup\hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] \hspace{0.05cm}\cup \hspace{0.05cm}[\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] \hspace{0.1cm}\right \} \hspace{0.05cm}.$$
Bitte beachten Sie:
- Das Ereignis $[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht unbedingt aus, dass beim betrachteten Empfangsvektor $\underline{y}$ tatsächlich für das Codewort $\underline{x}_{1}$ entschieden wird, sondern lediglich, dass die Entscheidung für $x_{1}$ aufgrund der Statistik sinnvoller wäre als die Entscheidung für $\underline{x}_{0}$.
- Es könnte aber auch für $\underline{x}_{2}$ oder $\underline{x}_{3}$ entschieden werden, wenn das "Maximum–Likelihood–Kriterium" hierfür spricht.
Die Berechnung der Blockfehlerwahrscheinlichkeit ist schwierig, da die Ereignisse $[\underline{x}_{0} → \underline{x}_{1}]$ , $[\underline{x}_{0} → \underline{x}_{2}]$ und $[\underline{x}_{0} → \underline{x}_{3}]$ nicht notwendigerweise disjunkt sind. Eine obere Schranke liefert die "Union Bound":
- $${\rm Pr(Union \hspace{0.15cm}Bound)} = {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] \ge {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$
Eine weitere Schranke wurde von Bhattacharyya angegeben:
- $${\rm Pr(Bhattacharyya)} = W(\beta)-1 \ge {\rm Pr(Union \hspace{0.15cm}Bound)} \ge {\rm Pr(Blockfehler)} \hspace{0.05cm},$$
wobei beim Binary Erasure Channel $\rm (BEC)$ für den Bhattacharyya–Parameter $\beta = \lambda$ gilt und $W(X)$ die Gewichtsfunktion angibt, wobei die Pseudo–Variable $X$ hier durch den Bhattacharyya–Parameter $\lambda$ zu ersetzen ist.
- Die Bhattacharyya–Schranke liegt je nach Kanal mehr oder weniger weit oberhalb der "Union Bound".
- Ihre Bedeutung liegt darin, dass die Schranke für unterschiedliche Kanäle in gleicher Weise angebbar ist.
Hinweis: Die Aufgabe gehört zum Kapitel "Schranken für die Blockfehlerwahrscheinlichkeit".
Fragebogen
Musterlösung
- $\underline{y} = (0, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^3 \ · \ (1 – \lambda)^2$,
- $\underline{y} = (0, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, 0, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^4 \ · \ (1 – \lambda)$,
- $\underline{y} = ({\rm E}, {\rm E}, {\rm E}, {\rm E}, {\rm E})$ mit Wahrscheinlichkeit $\lambda^5$.
Die Wahrscheinlichkeit, dass aufgrund des spezifischen Empfangsvektors $\underline{y}$ das Codewort $\underline{x}_{1}$ genau so wahrscheinlich ist wie $\underline{x}_{0}$, ergibt sich zu
- $$\ {\rm Pr}\ [\underline{x}_0 \hspace{0.12cm}{\rm und}\hspace{0.12cm} \underline{x}_1 \hspace{0.15cm}{\rm sind \hspace{0.15cm}gleichwahrscheinlich}] = \lambda^3 \cdot (1- \lambda)^2 + 2 \cdot \lambda^4 \cdot (1- \lambda) + \lambda^5 =\lambda^3 \cdot \left [ (1- \lambda)^2 + 2 \cdot \lambda \cdot (1- \lambda) + \lambda^2 \right ] = \lambda^3 \hspace{0.05cm}.$$
In diesem Fall entscheidet man sich nach dem Zufallsprinzip für $\underline{x}_{0}$ (wäre richtig) oder für $\underline{x}_{1}$ (leider falsch), und zwar mit gleicher Wahrscheinlichkeit. Daraus folgt:
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}1}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm}.$$
(2) Nach Teilaufgabe (1) ist die Antwort 2 richtig und nicht die Antwort 1. Auch die Aussage 3 ist falsch:
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ sagt nicht aus, dass mit dieser Wahrscheinlickeit das Codewort $\underline{x}_{0}$ tatsächlich in das falsche Codewort $\underline{x}_{1}$ übergeht, sondern nur, dass es mit dieser Wahrscheinlichkeit zu $\underline{x}_{1}$ übergehen könnte.
- ${\rm Pr}[\underline{x}_{0} → \underline{x}_{1}]$ beinhaltet auch Konstellationen, bei denen die Entscheidung tatsächlich für $\underline{x}_{2}$ bzw. $\underline{x}_{3}$ fällt.
(3) Wegen $d_{\rm H}(\underline{x}_{0}, \underline{x}_{2}) = 3$ und $d_{\rm H}(\underline{x}_{0}, \underline{x}_{3}) = 4$ ergibt sich hierfür
- $${\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}2}] = 1/2 \cdot \lambda^3 \hspace{0.15cm} \underline{= 0.5 \cdot 10^{-3}} \hspace{0.05cm},$$
- $$ {\rm Pr} [\underline{x}_{\hspace{0.02cm}0} \mapsto \underline{x}_{\hspace{0.02cm}3}] = 1/2 \cdot \lambda^4 \hspace{0.15cm} \underline{= 0.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(4) Die Blockfehlerwahrscheinlichkeit ist nie größer (mit einer gewissen Wahrscheinlichkeit eher kleiner) als die so genannte "Union Bound":
- $${\rm Pr(Union \hspace{0.15cm}Bound)} \hspace{-0.15cm}\ = \ \hspace{-0.15cm} {\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}1}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}2}] +{\rm Pr}[\underline{x}_{\hspace{0.02cm}0} \hspace{-0.02cm}\mapsto \hspace{-0.02cm} \underline{x}_{\hspace{0.02cm}3}] = 2 \cdot \lambda^3/2 + \lambda^4/2 = 0.001 + 0.00005 \hspace{0.15cm} \underline{= 1.05 \cdot 10^{-3}} \hspace{0.05cm}.$$
(5) Allgemein gilt:
- $${\rm Pr(Blockfehler) ≤ {\rm Pr(Union \hspace{0.15cm}Bound)} \le Pr(Bhattacharyya)} = W(\beta) - 1.$$
- Für das Distanzspektrum bzw. die Gewichtsfunktion erhält man im vorliegenden Fall:
- $$W_0 = 1 \hspace{0.05cm}, \hspace{0.2cm} W_3 = 2 \hspace{0.05cm}, \hspace{0.2cm}W_4 = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(X) = 1+ 2 \cdot X^{3} +X^{4} \hspace{0.05cm}.$$
- Beim BEC–Kanal gilt zudem $\beta = \lambda$. Daraus folgt als Endergebnis für $\lambda = 0.001$:
- $${\rm Pr(Bhattacharyya)} = 2 \cdot \lambda^3 + \lambda^4 \hspace{0.15cm} \underline{= 2.1 \cdot 10^{-3}} \hspace{0.05cm}.$$
- Anzumerken ist, dass beim BEC–Modell die "Bhattacharyya–Schranke" stets doppelt so groß ist wie die "Union Bound", die ja selbst wieder eine obere Schranke für die Blockfehlerwahrscheinlichkeit darstellt.