Aufgaben:Aufgabe 2.4: GF(2 hoch 2)–Darstellungsformen: Unterschied zwischen den Versionen
Aus LNTwww
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | {{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | ||
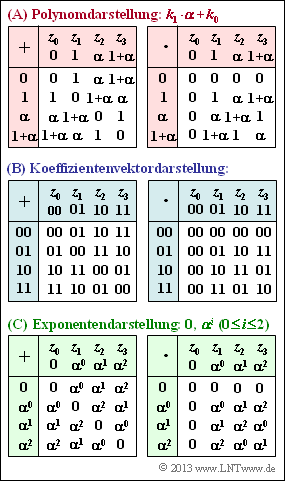
| − | [[Datei:P_ID2507__KC_A_2_4_neu.png|right|frame|Drei | + | [[Datei:P_ID2507__KC_A_2_4_neu.png|right|frame|Drei Darstellungsformen für ${\rm GF}(2^2)$]] |
Nebenstehend sehen Sie für den Erweiterungskörper $\rm GF(2^2)$ die Additions– sowie die Multiplikationstabelle in drei verschiedenen Varianten: | Nebenstehend sehen Sie für den Erweiterungskörper $\rm GF(2^2)$ die Additions– sowie die Multiplikationstabelle in drei verschiedenen Varianten: | ||
| − | * die Polynomdarstellung, | + | * die '''Polynomdarstellung''', |
| − | |||
| − | |||
| + | * die '''Koeffizientenvektordarstellung''', | ||
| + | * die '''Exponentendarstellung'''. | ||
| − | + | Hinweise: | |
| − | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Erweiterungsk%C3%B6rper|Erweiterungskörper]]. | + | * Die Aufgabe bezieht sich auf das Kapitel [[Kanalcodierung/Erweiterungsk%C3%B6rper|"Erweiterungskörper"]]. |
| − | * Alle notwendigen Informationen zu ${\rm GF}(2^2)$ finden Sie auf der [[Kanalcodierung/Erweiterungsk%C3%B6rper#GF.2822.29_.E2.80.93_Beispiel_eines_Erweiterungsk.C3.B6rpers|ersten Seite]] dieses Kapitels. | + | |
| − | * In der Teilaufgabe '''(4)''' werden folgende Ausdrücke betrachtet: | + | * Alle notwendigen Informationen zu ${\rm GF}(2^2)$ finden Sie auf der [[Kanalcodierung/Erweiterungsk%C3%B6rper#GF.2822.29_.E2.80.93_Beispiel_eines_Erweiterungsk.C3.B6rpers|"ersten Seite"]] dieses Kapitels. |
| + | |||
| + | * In der Teilaufgabe '''(4)''' werden folgende Ausdrücke betrachtet: | ||
:$$A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3,$$ | :$$A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3,$$ | ||
:$$B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3).$$ | :$$B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3).$$ | ||
| Zeile 26: | Zeile 28: | ||
{Welche Charakteristika erkennt man aus der Polynomdarstellung? | {Welche Charakteristika erkennt man aus der Polynomdarstellung? | ||
|type="[]"} | |type="[]"} | ||
| − | + Die Elemente $\alpha$ und $1 + \alpha$ sind weder $0$ noch $1$. | + | + Die Elemente "$\alpha$" und "$1 + \alpha$" sind weder $0$ noch $1$. |
+ Die Rechenoperationen erfolgen modulo $2$. | + Die Rechenoperationen erfolgen modulo $2$. | ||
- Die Rechenoperationen erfolgen modulo $4$. | - Die Rechenoperationen erfolgen modulo $4$. | ||
| − | - Man erkennt das Ergebnis $\alpha^2 + \alpha + 1 = 0$ aus der Additionstabelle. | + | - Man erkennt das Ergebnis "$\alpha^2 + \alpha + 1 = 0$" aus der Additionstabelle. |
| − | + Man erkennt das Ergebnis $\alpha^2 + \alpha + 1 = 0$ aus der Multiplikationstabelle. | + | + Man erkennt das Ergebnis "$\alpha^2 + \alpha + 1 = 0$" aus der Multiplikationstabelle. |
| − | {Welcher Zusammenhang besteht zwischen der Koeffizientenvektor– und der Polynomdarstellung? Es gelte $k_0 ∈ \{0, \, 1\}$ und $k_1 ∈ \{0, \, 1\}$. | + | {Welcher Zusammenhang besteht zwischen der Koeffizientenvektor– und der Polynomdarstellung? Es gelte $k_0 ∈ \{0, \, 1\}$ und $k_1 ∈ \{0, \, 1\}$. |
|type="()"} | |type="()"} | ||
| − | - $(k_0 \ k_1)$ bezieht sich auf das Element $k_1 \cdot \alpha + k_0$. | + | - "$(k_0 \ k_1)$" bezieht sich auf das Element "$k_1 \cdot \alpha + k_0$". |
| − | + $(k_1 \ k_0)$ bezieht sich auf das Element $k_1 \cdot \alpha + k_0$. | + | + "$(k_1 \ k_0)$" bezieht sich auf das Element "$k_1 \cdot \alpha + k_0$". |
- Zwischen beiden Darstellungen besteht keinerlei Zusammenhang. | - Zwischen beiden Darstellungen besteht keinerlei Zusammenhang. | ||
| Zeile 41: | Zeile 43: | ||
|type="[]"} | |type="[]"} | ||
- Es sind keine Zusammenhänge erkennbar. | - Es sind keine Zusammenhänge erkennbar. | ||
| − | + Die Elemente $0, | + | + Die Elemente "$0$", "$1$" und "$\alpha$" sind in beiden Darstellungen gleich. |
| − | + Das Element $1 + \alpha$ lautet in der Exponentendarstellung $\alpha^2$. | + | + Das Element "$1 + \alpha$" lautet in der Exponentendarstellung "$\alpha^2$". |
| − | - Das Element $\alpha^2$ der Exponentendarstellung steht für $\alpha \cdot (1 + \alpha)$. | + | - Das Element "$\alpha^2$" der Exponentendarstellung steht für "$\alpha \cdot (1 + \alpha)$". |
| − | {Berechnen Sie die Ausdrücke $A$ und $B$ nach diesen drei Darstellungsformen. Welche Aussagen treffen zu? | + | {Berechnen Sie die Ausdrücke $A$ und $B$ nach diesen drei Darstellungsformen. Welche Aussagen treffen zu? |
|type="[]"} | |type="[]"} | ||
+ Es gilt $A = z_0$, | + Es gilt $A = z_0$, | ||
| Zeile 55: | Zeile 57: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Zutreffend sind die <u>Lösungsvorschläge 1, 2 und 5</u>. | + | '''(1)''' Zutreffend sind die <u>Lösungsvorschläge 1, 2 und 5. Begründung</u>: |
| + | * Wäre $\alpha = 0$ oder $\alpha = 1$, so wäre das Pseudoelement $\alpha$ nicht mehr unterscheidbar von den beiden anderen ${\rm GF}(2)$–Elementen $0$ und $1$. | ||
| + | |||
| + | * Die Modulo–2–Rechnung erkennt man aus der Additionstabelle. Beispielsweise gilt $1 + 1 = 0, \ \alpha + \alpha = 0, \ (1 + \alpha) + (1 + \alpha) = 0$, usw. | ||
| − | + | * Aus der Multiplikationstabelle geht hervor, dass $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$ gilt $($3. Zeile, 3. Spalte$)$. Damit gilt auch | |
| − | |||
| − | |||
| − | * Aus der Multiplikationstabelle geht hervor, dass $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$ gilt (3. Zeile, 3. Spalte). Damit gilt auch | ||
:$$\alpha^2 + \alpha + 1 = 0.$$ | :$$\alpha^2 + \alpha + 1 = 0.$$ | ||
| − | '''(2)''' Richtig ist <u>Lösungsvorschlag 2</u>. So steht | + | '''(2)''' Richtig ist <u>Lösungsvorschlag 2</u>. So steht |
| − | * | + | *"$(0 \ 1)$" für das Element "$1$", und |
| − | * | + | |
| + | *"$(1 \ 0)$" für das Element "$0$". | ||
| + | |||
| − | '''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: |
| − | *Es gilt $\alpha^0 = 1$ und $\alpha^1 = \alpha$. | + | *Es gilt $\alpha^0 = 1$ und $\alpha^1 = \alpha$. |
| − | *Bei dem zugrundeliegenden Polynom $p(x) = x^2 + x + 1$ folgt aus $p(\alpha) = 0$ weiterhin: | + | |
| + | *Bei dem zugrundeliegenden Polynom $p(x) = x^2 + x + 1$ folgt aus $p(\alpha) = 0$ weiterhin: | ||
:$$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$ | :$$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$ | ||
| Zeile 84: | Zeile 89: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Richtig sind demnach die <u>Lösungsvorschläge 1 und 2</u>. | + | Richtig sind demnach die <u>Lösungsvorschläge 1 und 2</u>. |
| − | Zu den gleichen Ergebnissen kommt man mit der Koeffizientenvektordarstellung: | + | *Zu den gleichen Ergebnissen kommt man mit der Koeffizientenvektordarstellung: |
:$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 | :$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Zeile 92: | Zeile 97: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Und schließlich mit der Exponentendarstellung: | + | *Und schließlich mit der Exponentendarstellung: |
:$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = | :$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = | ||
\alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 | \alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 | ||
Aktuelle Version vom 2. Oktober 2022, 15:25 Uhr
Nebenstehend sehen Sie für den Erweiterungskörper $\rm GF(2^2)$ die Additions– sowie die Multiplikationstabelle in drei verschiedenen Varianten:
- die Polynomdarstellung,
- die Koeffizientenvektordarstellung,
- die Exponentendarstellung.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel "Erweiterungskörper".
- Alle notwendigen Informationen zu ${\rm GF}(2^2)$ finden Sie auf der "ersten Seite" dieses Kapitels.
- In der Teilaufgabe (4) werden folgende Ausdrücke betrachtet:
- $$A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3,$$
- $$B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3).$$
Fragebogen
Musterlösung
(1) Zutreffend sind die Lösungsvorschläge 1, 2 und 5. Begründung:
- Wäre $\alpha = 0$ oder $\alpha = 1$, so wäre das Pseudoelement $\alpha$ nicht mehr unterscheidbar von den beiden anderen ${\rm GF}(2)$–Elementen $0$ und $1$.
- Die Modulo–2–Rechnung erkennt man aus der Additionstabelle. Beispielsweise gilt $1 + 1 = 0, \ \alpha + \alpha = 0, \ (1 + \alpha) + (1 + \alpha) = 0$, usw.
- Aus der Multiplikationstabelle geht hervor, dass $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$ gilt $($3. Zeile, 3. Spalte$)$. Damit gilt auch
- $$\alpha^2 + \alpha + 1 = 0.$$
(2) Richtig ist Lösungsvorschlag 2. So steht
- "$(0 \ 1)$" für das Element "$1$", und
- "$(1 \ 0)$" für das Element "$0$".
(3) Richtig sind die Lösungsvorschläge 2 und 3:
- Es gilt $\alpha^0 = 1$ und $\alpha^1 = \alpha$.
- Bei dem zugrundeliegenden Polynom $p(x) = x^2 + x + 1$ folgt aus $p(\alpha) = 0$ weiterhin:
- $$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$
(4) Entsprechend den Tabellen der Polynomdarstellung gilt:
- $$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha \cdot \alpha + \alpha \cdot (1+\alpha) + (1+\alpha) \cdot (1+\alpha) = (1+\alpha) + (1) + (\alpha) = 0 = z_0 \hspace{0.05cm},$$
- $$ B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = (0 + 1 + \alpha) \cdot (0 + 1 + 1+ \alpha) = (1+\alpha) \cdot \alpha = 1 = z_1 \hspace{0.05cm}.$$
Richtig sind demnach die Lösungsvorschläge 1 und 2.
- Zu den gleichen Ergebnissen kommt man mit der Koeffizientenvektordarstellung:
- $$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 \hspace{0.05cm},$$
- $$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [(00) + (01) + (10)] \cdot [(00) + (01) + (11)] =(11) \cdot (10) = (01) = z_1 \hspace{0.05cm}.$$
- Und schließlich mit der Exponentendarstellung:
- $$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = \alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 \hspace{0.05cm},$$
- $$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = [0 + \alpha^0 + \alpha^1] \cdot [0 + \alpha^0 + \alpha^2] = \alpha^2 \cdot \alpha^1 = \alpha^3 = \alpha^0 = z_1 \hspace{0.05cm}.$$