Aufgaben:Aufgabe 2.16: Entscheidungskriterien bei BDD: Unterschied zwischen den Versionen
Aus LNTwww
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
[[Datei: P_ID2583__KC_A_2_16neu.png|right|frame|Betrachtete Codierraumschemata]] | [[Datei: P_ID2583__KC_A_2_16neu.png|right|frame|Betrachtete Codierraumschemata]] | ||
| − | Wir gehen von einem Blockcode der Länge $n$ mit Symbolen $c_i ∈ {\rm GF}(2^m)$ aus, der bis zu $t$ Symbole korrigieren kann. Jedes mögliche Empfangswort $\underline{y}_i$ kann dann als ein Punkt in einem hochdimensionalen Raum angesehen werden | + | Wir gehen von einem Blockcode der Länge $n$ mit Symbolen $c_i ∈ {\rm GF}(2^m)$ aus, der bis zu $t$ Symbole korrigieren kann. |
| + | *Jedes mögliche Empfangswort $\underline{y}_i$ kann dann als ein Punkt in einem hochdimensionalen Raum angesehen werden. | ||
| − | + | *Geht man von der Basis ${\rm GF}(2) = \{0, \, 1\}$ aus, so beträgt die Dimension $n \cdot m$. | |
| − | |||
| − | |||
| − | + | Die Grafik zeigt einen solchen Raum in vereinfachender, schematischer zweidimensionaler Darstellung. Die Abbildung ist wie folgt zu interpretieren: | |
| + | # Gesendet wurde der rote Punkt $\underline{c}_j$. Alle rot umrandeten Punkte $\underline{y}_i$ in einer Hyperkugel um diesen Punkt $\underline{c}_j$ mit dem Parameter $t$ als Radius können korrigiert werden. Mit der Nomenklatur gemäß der [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete#Blockfehlerwahrscheinlichkeit_f.C3.BCr_RSC_und_BDD|$\rm Grafik$]] im Theorieteil gilt $\underline{z}_i = \underline{c}_j$ <br>⇒ „Die Fehlerkorrektur ist erfolgreich”. | ||
| + | # Bei sehr vielen Symbolfehlern kann $\underline{c}_j$ in einen blauen $($oder weißblauen$)$ Punkt $\underline{y}_j$ verfälscht werden, der zur Hyperkugel eines anderen Codewortes $\underline{c}_{k ≠ j}$ gehört. In diesem Fall trifft der Decoder eine falsche Entscheidung <br>⇒ „Das Empfangswort $\underline{y}_j$ wird falsch decodiert”. | ||
| + | # Schließlich kann es wie in der unteren Skizze auch noch gelbe Punkte geben, die zu keiner Hyperkugel gehören <br>⇒ „Das Empfangswort $\underline{y}_j$ ist nicht decodierbar”. | ||
| − | |||
| + | In dieser Aufgabe sollen Sie entscheiden, welches der beiden Coderaumschemata geeignet ist zur Beschreibung von | ||
| + | * [[Kanalcodierung/Beispiele_bin%C3%A4rer_Blockcodes#Hamming.E2.80.93Codes|Bounded Distance Decoding von Hamming–Codes]] bzw. | ||
| − | + | * [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete#Blockfehlerwahrscheinlichkeit_f.C3.BCr_RSC_und_BDD|Bounded Distance Decoding von Reed–Solomon–Codes]]. | |
| − | |||
| − | * [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete#Blockfehlerwahrscheinlichkeit_f.C3.BCr_RSC_und_BDD|Bounded Distance Decoding | ||
| Zeile 23: | Zeile 24: | ||
| + | <u>Hinweise:</u> | ||
| + | * Die Aufgabe ergänzt die Thematik des Kapitels [[Kanalcodierung/Fehlerwahrscheinlichkeit_und_Anwendungsgebiete|"Fehlerwahrscheinlichkeit und Anwendungsgebiete"]]. | ||
| − | |||
| − | |||
| − | |||
* Sie soll signifikante Unterschiede bei der Decodierung von Reed–Solomon–Codes und Hamming–Codes verdeutlichen. | * Sie soll signifikante Unterschiede bei der Decodierung von Reed–Solomon–Codes und Hamming–Codes verdeutlichen. | ||
| Zeile 38: | Zeile 38: | ||
- Codierraumschema $\rm B$. | - Codierraumschema $\rm B$. | ||
| − | {Welche Aussage gilt für die Wahrscheinlichkeit, dass bei Hamming–Codierung ein Empfangswort $\underline{y}$ nicht decodiert werden kann? | + | {Welche Aussage gilt für die Wahrscheinlichkeit, dass bei Hamming–Codierung ein Empfangswort $\underline{y}$ nicht decodiert werden kann? |
|type="[]"} | |type="[]"} | ||
| − | + Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt Null. | + | + Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \hspace{0.15cm}ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar)$ ist exakt Null. |
| − | - ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich Null, aber vernachlässigbar. | + | - ${\rm Pr}(\underline{y} \rm \hspace{0.15cm} ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar)$ ist ungleich Null, aber vernachlässigbar. |
| − | - Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$. | + | - Es gilt ${\rm Pr}(\underline{y} {\rm \hspace{0.15cm} ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar}) > {\rm Pr}(\underline{y} \rm \hspace{0.15cm} wird \hspace{0.15cm} falsch \hspace{0.15cm} decodiert)$. |
{Welches Codierraumschema trifft für die Reed–Solomon–Codes zu? | {Welches Codierraumschema trifft für die Reed–Solomon–Codes zu? | ||
| Zeile 51: | Zeile 51: | ||
{Welche Aussage gilt für die Wahrscheinlichkeit, dass ein Empfangswort $\underline{y}$ nach Reed–Solomon–Codierung nicht decodiert werden kann? | {Welche Aussage gilt für die Wahrscheinlichkeit, dass ein Empfangswort $\underline{y}$ nach Reed–Solomon–Codierung nicht decodiert werden kann? | ||
|type="[]"} | |type="[]"} | ||
| − | - Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist exakt Null. | + | - Die Wahrscheinlichkeit ${\rm Pr}(\underline{y} \rm \hspace{0.15cm}ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar)$ ist exakt Null. |
| − | - ${\rm Pr}(\underline{y} \rm \ ist \ nicht \ decodierbar)$ ist ungleich Null, aber vernachlässigbar. | + | - ${\rm Pr}(\underline{y} \rm \hspace{0.15cm} ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar)$ ist ungleich Null, aber vernachlässigbar. |
| − | + Es gilt ${\rm Pr}(\underline{y} {\rm \ ist \ nicht \ decodierbar}) > {\rm Pr}(\underline{y} \rm \ wird \ falsch \ decodiert)$. | + | + Es gilt ${\rm Pr}(\underline{y} {\rm \hspace{0.15cm} ist \hspace{0.15cm} nicht \hspace{0.15cm} decodierbar}) > {\rm Pr}(\underline{y} \rm \hspace{0.15cm} wird \hspace{0.15cm} falsch \hspace{0.15cm} decodiert)$. |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Richtig ist der <u>Lösungsvorschlag 1</u>, da das Codierraumschema | + | '''(1)''' Richtig ist der <u>Lösungsvorschlag 1</u>, da das Codierraumschema $\rm A$ einen perfekten Code beschreibt und jeder Hamming–Code $(n, \, k, \, 3)$ ein perfekter Code ist: |
| − | *Bei einem jeden Hamming–Code $(n, \, k, \, 3)$ gibt es insgesamt $2^n$ mögliche Empfangsworte $\underline{y}_i$, die bei der Syndromdecodierung einem von $2^k$ möglichen Codeworten $\underline{c}_j$ zugeordnet werden. | + | *Bei einem jeden Hamming–Code $(n, \, k, \, 3)$ gibt es insgesamt $2^n$ mögliche Empfangsworte $\underline{y}_i$, die bei der Syndromdecodierung einem von $2^k$ möglichen Codeworten $\underline{c}_j$ zugeordnet werden. |
| − | *Aufgrund der HC–Eigenschaft $d_{\rm min} = 3$ haben alle Kugeln im $n$–dimensionalen Raum den Radius $t = 1$. In allen Kugeln gibt es somit $2^{n-k}$ Punkte, zum Beispiel | + | |
| − | :* | + | *Aufgrund der HC–Eigenschaft $d_{\rm min} = 3$ haben alle Kugeln im $n$–dimensionalen Raum den Radius $t = 1$. In allen Kugeln gibt es somit $2^{n-k}$ Punkte, zum Beispiel |
| − | :* | + | :* $\text{HC (7, 4, 3)}$: einen Punkt für die fehlerfreie Übertragung und sieben Punkte für einen Bitfehler ⇒ $1 + 7 = 8 = 2^3 = 2^{7-4}$. |
| + | :* $\text{HC (15, 11, 3)}$: einen Punkt für die fehlerfreie Übertragung und nun fünfzehn Punkte für einen Bitfehler ⇒ $1 + 15 = 16 = 2^4 = 2^{15-11}$. | ||
| + | <u>Hinweis:</u> Da der Hamming–Code ein Binärcode ist, hat hier der Coderaum die Dimension $n$. | ||
| − | |||
| − | '''(2)''' Richtig ist die <u>Antwort 1</u>: | + | '''(2)''' Richtig ist die <u>Antwort 1</u>: |
*Im grauen Bereich außerhalb von „Kugeln” gibt es bei einem perfekten Code keinen einzigen Punkt. | *Im grauen Bereich außerhalb von „Kugeln” gibt es bei einem perfekten Code keinen einzigen Punkt. | ||
| − | |||
| + | *Dies wurde auch in der Rechnung zur Teilaufgabe '''(1)''' gezeigt. | ||
| − | '''(3)''' Die Reed–Solomon–Codes werden durch das Codierraumschema | + | |
| − | *Hier gibt es zahlreiche gelbe Punkte im grauen Bereich, also Punkte die bei | + | |
| − | *Betrachten wir beispielweise den $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Codeparametern $n = 7, \, k = 3$ und $t = 2$, so gibt es hier insgesamt $8^7 = 2097152$ Punkte und $8^3 = 512$ Hyperkugeln. | + | '''(3)''' Die Reed–Solomon–Codes werden durch das Codierraumschema $\rm B$ beschrieben ⇒ <u>Antwort 2</u>. |
| − | *Wäre dieser Code perfekt, so müsste es also innerhalb jeder Kugel $8^4 = 4096$ Punkte geben. Es gilt aber: | + | *Hier gibt es zahlreiche gelbe Punkte im grauen Bereich, also Punkte die bei "Bounded Distance Decoding" keiner Kugel zugeordnet werden können. |
| + | |||
| + | *Betrachten wir beispielweise den $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Codeparametern $n = 7, \, k = 3$ und $t = 2$, so gibt es hier insgesamt $8^7 = 2097152$ Punkte und $8^3 = 512$ Hyperkugeln. | ||
| + | |||
| + | *Wäre dieser Code perfekt, so müsste es also innerhalb jeder Kugel $8^4 = 4096$ Punkte geben. Es gilt aber: | ||
:$${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} | :$${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} | ||
= {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 | = {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Für ${\rm Pr}(f = 1)$ ist berücksichtigt, dass es & | + | *Für ${\rm Pr}(f = 1)$ ist berücksichtigt, dass es "$7 \rm \ über \ 1$" $= 7$ Fehlerpositionen geben kann, und für jede Fehlerposition auch sieben unterschiedliche Fehlerwerte. Entsprechendes ist auch für ${\rm Pr}(f = 2)$ berücksichtigt. |
| + | |||
| − | '''(4)''' Richtig ist die <u>Antwort 3</u>: | + | '''(4)''' Richtig ist die <u>Antwort 3</u>: |
| − | *Ein Punkt im grauen Niemandsland wird mit weniger Symbolfehlern erreicht als ein Punkt in einer anderen Hyperkugel. | + | *Ein Punkt im grauen Niemandsland wird mit weniger Symbolfehlern erreicht als ein Punkt in einer anderen Hyperkugel. |
| + | |||
*Für lange Codes wird in der Literatur eine obere Schranke für die Verfälschungswahrscheinlichkeit angegeben: | *Für lange Codes wird in der Literatur eine obere Schranke für die Verfälschungswahrscheinlichkeit angegeben: | ||
| Zeile 91: | Zeile 98: | ||
= {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} | = {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Für den ${\rm RSC} \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$ liefert diese obere Schranke den Wert $1/(16!) < 10^{-14}$. | + | *Für den ${\rm RSC} \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$ liefert diese obere Schranke den Wert $1/(16!) < 10^{-14}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 2. November 2022, 17:27 Uhr
Wir gehen von einem Blockcode der Länge $n$ mit Symbolen $c_i ∈ {\rm GF}(2^m)$ aus, der bis zu $t$ Symbole korrigieren kann.
- Jedes mögliche Empfangswort $\underline{y}_i$ kann dann als ein Punkt in einem hochdimensionalen Raum angesehen werden.
- Geht man von der Basis ${\rm GF}(2) = \{0, \, 1\}$ aus, so beträgt die Dimension $n \cdot m$.
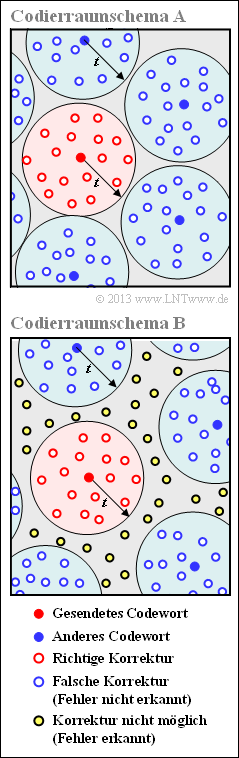
Die Grafik zeigt einen solchen Raum in vereinfachender, schematischer zweidimensionaler Darstellung. Die Abbildung ist wie folgt zu interpretieren:
- Gesendet wurde der rote Punkt $\underline{c}_j$. Alle rot umrandeten Punkte $\underline{y}_i$ in einer Hyperkugel um diesen Punkt $\underline{c}_j$ mit dem Parameter $t$ als Radius können korrigiert werden. Mit der Nomenklatur gemäß der $\rm Grafik$ im Theorieteil gilt $\underline{z}_i = \underline{c}_j$
⇒ „Die Fehlerkorrektur ist erfolgreich”. - Bei sehr vielen Symbolfehlern kann $\underline{c}_j$ in einen blauen $($oder weißblauen$)$ Punkt $\underline{y}_j$ verfälscht werden, der zur Hyperkugel eines anderen Codewortes $\underline{c}_{k ≠ j}$ gehört. In diesem Fall trifft der Decoder eine falsche Entscheidung
⇒ „Das Empfangswort $\underline{y}_j$ wird falsch decodiert”. - Schließlich kann es wie in der unteren Skizze auch noch gelbe Punkte geben, die zu keiner Hyperkugel gehören
⇒ „Das Empfangswort $\underline{y}_j$ ist nicht decodierbar”.
In dieser Aufgabe sollen Sie entscheiden, welches der beiden Coderaumschemata geeignet ist zur Beschreibung von
Hinweise:
- Die Aufgabe ergänzt die Thematik des Kapitels "Fehlerwahrscheinlichkeit und Anwendungsgebiete".
- Sie soll signifikante Unterschiede bei der Decodierung von Reed–Solomon–Codes und Hamming–Codes verdeutlichen.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 1, da das Codierraumschema $\rm A$ einen perfekten Code beschreibt und jeder Hamming–Code $(n, \, k, \, 3)$ ein perfekter Code ist:
- Bei einem jeden Hamming–Code $(n, \, k, \, 3)$ gibt es insgesamt $2^n$ mögliche Empfangsworte $\underline{y}_i$, die bei der Syndromdecodierung einem von $2^k$ möglichen Codeworten $\underline{c}_j$ zugeordnet werden.
- Aufgrund der HC–Eigenschaft $d_{\rm min} = 3$ haben alle Kugeln im $n$–dimensionalen Raum den Radius $t = 1$. In allen Kugeln gibt es somit $2^{n-k}$ Punkte, zum Beispiel
- $\text{HC (7, 4, 3)}$: einen Punkt für die fehlerfreie Übertragung und sieben Punkte für einen Bitfehler ⇒ $1 + 7 = 8 = 2^3 = 2^{7-4}$.
- $\text{HC (15, 11, 3)}$: einen Punkt für die fehlerfreie Übertragung und nun fünfzehn Punkte für einen Bitfehler ⇒ $1 + 15 = 16 = 2^4 = 2^{15-11}$.
Hinweis: Da der Hamming–Code ein Binärcode ist, hat hier der Coderaum die Dimension $n$.
(2) Richtig ist die Antwort 1:
- Im grauen Bereich außerhalb von „Kugeln” gibt es bei einem perfekten Code keinen einzigen Punkt.
- Dies wurde auch in der Rechnung zur Teilaufgabe (1) gezeigt.
(3) Die Reed–Solomon–Codes werden durch das Codierraumschema $\rm B$ beschrieben ⇒ Antwort 2.
- Hier gibt es zahlreiche gelbe Punkte im grauen Bereich, also Punkte die bei "Bounded Distance Decoding" keiner Kugel zugeordnet werden können.
- Betrachten wir beispielweise den $\rm RSC \, (7, \, 3, \, 5)_8$ mit den Codeparametern $n = 7, \, k = 3$ und $t = 2$, so gibt es hier insgesamt $8^7 = 2097152$ Punkte und $8^3 = 512$ Hyperkugeln.
- Wäre dieser Code perfekt, so müsste es also innerhalb jeder Kugel $8^4 = 4096$ Punkte geben. Es gilt aber:
- $${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}liegt\hspace{0.1cm} innerhalb\hspace{0.1cm} der\hspace{0.1cm} roten\hspace{0.1cm} Kugel)} = {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 \hspace{0.05cm}.$$
- Für ${\rm Pr}(f = 1)$ ist berücksichtigt, dass es "$7 \rm \ über \ 1$" $= 7$ Fehlerpositionen geben kann, und für jede Fehlerposition auch sieben unterschiedliche Fehlerwerte. Entsprechendes ist auch für ${\rm Pr}(f = 2)$ berücksichtigt.
(4) Richtig ist die Antwort 3:
- Ein Punkt im grauen Niemandsland wird mit weniger Symbolfehlern erreicht als ein Punkt in einer anderen Hyperkugel.
- Für lange Codes wird in der Literatur eine obere Schranke für die Verfälschungswahrscheinlichkeit angegeben:
- $${\rm Pr}(\underline{y}_{i} {\rm \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} = {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} \hspace{0.05cm}.$$
- Für den ${\rm RSC} \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$ liefert diese obere Schranke den Wert $1/(16!) < 10^{-14}$.