Aufgaben:Aufgabe 3.6: Gerades und ungerades Zeitsignal: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
[[Datei:P_ID516__Sig_A_3_6_neu.png|250px|right|frame|„Keilfunktion” sowie ein gerades und ein ungerades Zeitsignal]] | [[Datei:P_ID516__Sig_A_3_6_neu.png|250px|right|frame|„Keilfunktion” sowie ein gerades und ein ungerades Zeitsignal]] | ||
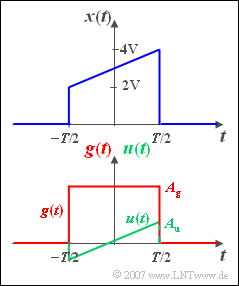
| − | Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $+T/2$ linear von $2\,\text{ V}$ auf $4\,\text{ V}$ ansteigt und außerhalb Null ist. | + | Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $+T/2$ linear von $2\,\text{V}$ auf $4\,\text{V}$ ansteigt und außerhalb Null ist. |
Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ werden als bekannt vorausgesetzt: | Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ werden als bekannt vorausgesetzt: | ||
| Zeile 27: | Zeile 27: | ||
*Alle diese Gesetzmäßigkeiten werden im Lernvideo [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] an Beispielen verdeutlicht. | *Alle diese Gesetzmäßigkeiten werden im Lernvideo [[Gesetzmäßigkeiten_der_Fouriertransformation_(Lernvideo)|Gesetzmäßigkeiten der Fouriertransformation]] an Beispielen verdeutlicht. | ||
*Lösen Sie diese Aufgabe mit Hilfe des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Zuordnungssatzes]]. | *Lösen Sie diese Aufgabe mit Hilfe des [[Signaldarstellung/Gesetzmäßigkeiten_der_Fouriertransformation#Zuordnungssatz|Zuordnungssatzes]]. | ||
| − | *Verwenden Sie für die beiden ersten Teilaufgaben die Signalparameter $A_u = 1\,\text{ V}$ und $T = 1\,\text{ ms}$. | + | *Verwenden Sie für die beiden ersten Teilaufgaben die Signalparameter $A_u = 1\,\text{V}$ und $T = 1\,\text{ms}$. |
| Zeile 41: | Zeile 41: | ||
{Wie groß ist der Spektralwert von $u(t)$ bei der Frequenz $f = 0$? | {Wie groß ist der Spektralwert von $u(t)$ bei der Frequenz $f = 0$? | ||
| − | + | <u>Hinweis</u>: Lieber denken als rechnen. | |
|type="{}"} | |type="{}"} | ||
${\rm Im}\big[U(f=0)\big]\ = \ $ { 0. } $\text{mV/Hz}$ | ${\rm Im}\big[U(f=0)\big]\ = \ $ { 0. } $\text{mV/Hz}$ | ||
| Zeile 61: | Zeile 61: | ||
*Der Imaginärteil ist zahlenmäßig ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$. | *Der Imaginärteil ist zahlenmäßig ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$. | ||
| − | *Dagegen liefert die si-Funktion bei $f \cdot T = 1$ den Wert Null, während der Cosinus gleich $-1$ ist. Damit erhält man mit $A_u = 1\,\text{V}$ und $T = 1\,\text{ms}$: | + | *Dagegen liefert die si-Funktion bei $f \cdot T = 1$ den Wert Null, während der Cosinus gleich $-1$ ist. |
| + | * Damit erhält man mit $A_u = 1\,\text{V}$ und $T = 1\,\text{ms}$: | ||
:$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | :$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | ||
| Zeile 68: | Zeile 69: | ||
'''(2)''' Eine ungerade Zeitfunktion $u(t)$ besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum: | '''(2)''' Eine ungerade Zeitfunktion $u(t)$ besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum: | ||
| − | $U( { - f} ) = - U( f ).$ Mit dem Grenzübergang $f \rightarrow \infty$ folgt aus der angegebenen Gleichung | + | $U( { - f} ) = - U( f ).$ Mit dem Grenzübergang $f \rightarrow \infty$ folgt aus der angegebenen Gleichung |
:$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | :$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | ||
| − | das Ergebnis $U(f = 0) = 0$. Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen. | + | das Ergebnis $U(f = 0) = 0$. Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen. |
Wir gehen etwas pragmatischer vor. | Wir gehen etwas pragmatischer vor. | ||
| Zeile 86: | Zeile 87: | ||
'''(3)''' Das Signal $x(t)$ kann in den geraden und den ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. ungeraden Imaginärteil von $X(f)$ führen: | '''(3)''' Das Signal $x(t)$ kann in den geraden und den ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. ungeraden Imaginärteil von $X(f)$ führen: | ||
| − | *Der gerade Anteil ist gleich der Funktion $g(t)$ mit $A_g = 3\,\text{V}$. Daraus folgt für den Realteil des Spektralwertes bei $f \cdot T = 0.5$: | + | *Der gerade Anteil ist gleich der Funktion $g(t)$ mit $A_g = 3\,\text{V}$. Daraus folgt für den Realteil des Spektralwertes bei $f \cdot T = 0.5$: |
:$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | *Der Imaginärteil ergibt sich aus der Spektralfunktion $U(f)$ mit $A_u = 1\,\text{V}$. Dieser wurde bereits in der Teilaufgabe '''(1)''' berechnet: | + | *Der Imaginärteil ergibt sich aus der Spektralfunktion $U(f)$ mit $A_u = 1\,\text{V}$. Dieser wurde bereits in der Teilaufgabe '''(1)''' berechnet: |
:$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
Aktuelle Version vom 27. April 2021, 14:47 Uhr
Gesucht ist das Spektrum $X(f)$ des nebenstehend skizzierten impulsförmigen Signals $x(t)$, das im Bereich von $–T/2$ bis $+T/2$ linear von $2\,\text{V}$ auf $4\,\text{V}$ ansteigt und außerhalb Null ist.
Die Spektralfunktionen der unten dargestellten Signale $g(t)$ und $u(t)$ werden als bekannt vorausgesetzt:
- Die gerade, rechteckförmige Zeitfunktion $g(t)$ hat das Spektrum
- $$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{mit}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = {\sin ( x )}/{x}.$$
- Das Spektrum der unsymmetrischen Funktion $u(t)$ lautet:
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big].$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Gesetzmäßigkeiten der Fouriertransformation.
- Alle diese Gesetzmäßigkeiten werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.
- Lösen Sie diese Aufgabe mit Hilfe des Zuordnungssatzes.
- Verwenden Sie für die beiden ersten Teilaufgaben die Signalparameter $A_u = 1\,\text{V}$ und $T = 1\,\text{ms}$.
Fragebogen
Musterlösung
- $$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$
- Der Imaginärteil ist zahlenmäßig ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$.
- Dagegen liefert die si-Funktion bei $f \cdot T = 1$ den Wert Null, während der Cosinus gleich $-1$ ist.
- Damit erhält man mit $A_u = 1\,\text{V}$ und $T = 1\,\text{ms}$:
- $$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$
(2) Eine ungerade Zeitfunktion $u(t)$ besitzt nach dem Zuordnungssatz stets ein imaginäres und gleichzeitig ungerades Spektrum: $U( { - f} ) = - U( f ).$ Mit dem Grenzübergang $f \rightarrow \infty$ folgt aus der angegebenen Gleichung
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$
das Ergebnis $U(f = 0) = 0$. Formal könnte man dieses Ergebnis durch Anwendung der l'Hospitalschen Regel bestätigen.
Wir gehen etwas pragmatischer vor.
- Setzen wir zum Beispiel $f \cdot T = 0.01$, so erhält man:
- $$U( {f \cdot T = 0.01}) = -{\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}\big[ {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} \big ] = - {\rm{j}} \cdot \frac{ {A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$
- Für noch kleinere Frequenzwerte wird auch das Ergebnis immer kleiner.
- Schneller kommt man zum Ergebnis $U(f = 0)\;\underline{ = 0}$, wenn man berücksichtigt, dass das Integral über $u(t)$ verschwindet.
- Man muss also gar nicht rechnen.
(3) Das Signal $x(t)$ kann in den geraden und den ungeraden Anteil aufgeteilt werden, die zum geraden Realteil bzw. ungeraden Imaginärteil von $X(f)$ führen:
- Der gerade Anteil ist gleich der Funktion $g(t)$ mit $A_g = 3\,\text{V}$. Daraus folgt für den Realteil des Spektralwertes bei $f \cdot T = 0.5$:
- $${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$
- Der Imaginärteil ergibt sich aus der Spektralfunktion $U(f)$ mit $A_u = 1\,\text{V}$. Dieser wurde bereits in der Teilaufgabe (1) berechnet:
- $${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$