Aufgaben:Aufgabe 5.1Z: Abtastung harmonischer Schwingungen: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
Angenommen wird, dass die Signale äquidistant zu den Zeitpunkten $\nu \cdot T_{\rm A}$ abgetastet werden, wobei die Parameterwerte $T_{\rm A} = 80 \ µ \text{s}$ und $T_{\rm A} = 100 \ µ \text{s}$ analysiert werden sollen. | Angenommen wird, dass die Signale äquidistant zu den Zeitpunkten $\nu \cdot T_{\rm A}$ abgetastet werden, wobei die Parameterwerte $T_{\rm A} = 80 \ µ \text{s}$ und $T_{\rm A} = 100 \ µ \text{s}$ analysiert werden sollen. | ||
| − | Die Signalrekonstruktion beim Empfänger erfolgt durch einen Tiefpass $H(f)$, der aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ das | + | Die Signalrekonstruktion beim Empfänger erfolgt durch einen Tiefpass $H(f)$, der aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ das Ausgangssignal $y(t)$ formt. Es gelte: |
:$$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ | :$$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ | ||
0 \\ \end{array} \right.\quad | 0 \\ \end{array} \right.\quad | ||
| Zeile 22: | Zeile 22: | ||
|f| > f_{\rm G} \hspace{0.05cm}, \\ | |f| > f_{\rm G} \hspace{0.05cm}, \\ | ||
\end{array}$$ | \end{array}$$ | ||
| − | Hierbei gibt $f_{\rm G}$ die Grenzfrequenz des rechteckförmigen Tiefpassfilters an. Für diese soll gelten: | + | Hierbei gibt $f_{\rm G}$ die Grenzfrequenz des rechteckförmigen Tiefpassfilters an. Für diese soll gelten: |
:$$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$ | :$$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$ | ||
Das Abtasttheorem ist erfüllt, wenn $y(t) = x(t)$ gilt. | Das Abtasttheorem ist erfüllt, wenn $y(t) = x(t)$ gilt. | ||
| Zeile 34: | Zeile 34: | ||
*Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Zeitdiskrete_Signaldarstellung|Zeitdiskrete Signaldarstellung]]. | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Zeitdiskrete_Signaldarstellung|Zeitdiskrete Signaldarstellung]]. | ||
| − | *Zu der hier behandelten Thematik gibt es ein interaktives Applet: [[Applets: | + | *Zu der hier behandelten Thematik gibt es ein interaktives Applet: [[Applets:Abtastung_analoger_Signale_und_Signalrekonstruktion|Abtastung analoger Signale und Signalrekonstruktion]] |
| Zeile 40: | Zeile 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß sind Amplitude und Frequenz der Signale $x_1(t)$, $x_2(t)$ und $x_3(t)$? | + | {Wie groß sind entsprechend der Grafik die Amplitude und die Frequenz der Signale $x_1(t)$, $x_2(t)$ und $x_3(t)$? |
|type="{}"} | |type="{}"} | ||
$A \hspace{0.25cm} = \ $ { 2 3% } $\text{V}$ | $A \hspace{0.25cm} = \ $ { 2 3% } $\text{V}$ | ||
| Zeile 53: | Zeile 53: | ||
| − | {Wie lautet das rekonstruierte Signal $y_1(t) = A_1 \cdot \cos (2\pi f_0 t – \varphi_1)$ mit dem Abtastabstand $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$? Interpretieren Sie das Ergebnis. | + | {Wie lautet das rekonstruierte Signal $y_1(t) = A_1 \cdot \cos (2\pi f_0 t – \varphi_1)$ mit dem Abtastabstand $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$? Interpretieren Sie das Ergebnis. |
|type="{}"} | |type="{}"} | ||
$A_1\hspace{0.2cm} = \ ${ 2 3% } $\text{V}$ | $A_1\hspace{0.2cm} = \ ${ 2 3% } $\text{V}$ | ||
| Zeile 59: | Zeile 59: | ||
| − | {Welche Amplitude $A_2$ besitzt das rekonstruierte Signal $y_2(t)$, wenn das Sinussignal $x_2(t)$ anliegt? Es gelte weiterhin $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$. | + | {Welche Amplitude $A_2$ besitzt das rekonstruierte Signal $y_2(t)$, wenn das Sinussignal $x_2(t)$ anliegt? Es gelte weiterhin $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$. |
|type="{}"} | |type="{}"} | ||
$A_2\hspace{0.2cm} = \ $ { 0. } $\text{V}$ | $A_2\hspace{0.2cm} = \ $ { 0. } $\text{V}$ | ||
| − | {Welche Amplitude $A_3$ besitzt das rekonstruierte Signal $y_3(t)$, wenn das Signal $x_3(t)$ anliegt? Es gelte weiterhin $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$. | + | {Welche Amplitude $A_3$ besitzt das rekonstruierte Signal $y_3(t)$, wenn das Signal $x_3(t)$ anliegt? Es gelte weiterhin $\underline{T_{\rm A} = 100 \ {\rm µ} \text{s}}$. |
|type="{}"} | |type="{}"} | ||
$A_3\hspace{0.2cm} = \ $ { 1 3% } $\text{V}$ | $A_3\hspace{0.2cm} = \ $ { 1 3% } $\text{V}$ | ||
| Zeile 74: | Zeile 74: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Aus der Grafik erkennt man die Amplitude $\underline{A = 2\ \text{V}}$ sowie die Periodendauer $T_0 = 0.2 \ \text{ms}$. Daraus ergibt sich die Signalfrequenz $f_0 = 1/T_0 \; \underline{= 5 \ \text{kHz}}$. | + | '''(1)''' Aus der Grafik erkennt man die Amplitude $\underline{A = 2\ \text{V}}$ sowie die Periodendauer $T_0 = 0.2 \ \text{ms}$. |
| + | *Daraus ergibt sich die Signalfrequenz $f_0 = 1/T_0 \; \underline{= 5 \ \text{kHz}}$. | ||
'''(2)''' Richtig sind <u>alle Löungsvorschläge</u>: | '''(2)''' Richtig sind <u>alle Löungsvorschläge</u>: | ||
| − | *Die Abtastrate | + | *Die Abtastrate beträgt hier $f_{\rm A} = 1/T_{\rm A} = 12.5 \ \text{kHz}$. |
| − | *Dieser Wert ist größer als $2 \cdot f_0 = 10 \ \text{kHz}$. | + | *Dieser Wert ist größer als $2 \cdot f_0 = 10 \ \text{kHz}$. |
| − | *Damit ist das Abtasttheorem unabhängig von der Phase erfüllt, und es gilt stets $y(t) = x(t)$. | + | *Damit ist das Abtasttheorem unabhängig von der Phase erfüllt, und es gilt stets $y(t) = x(t)$. |
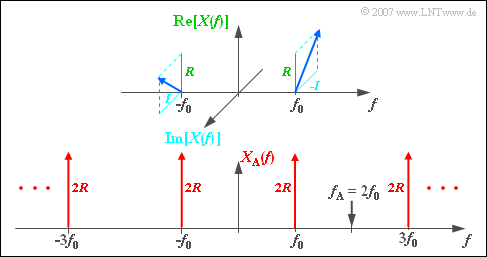
| − | [[Datei:P_ID1130__Sig_Z_5_1_c.png|right|frame|Spektrum $X_{\rm A}(f)$ des abgetasteten Signals – Realteil und Imaginärteil]] | + | [[Datei:P_ID1130__Sig_Z_5_1_c.png|right|frame|Spektrum $X_{\rm A}(f)$ des abgetasteten Signals – Realteil und Imaginärteil]] |
| − | '''(3)''' Die Abtastrate beträgt nun $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$. | + | '''(3)''' Die Abtastrate beträgt nun $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$. |
| − | *Nur im Sonderfall des Cosinussignals ist | + | *Nur im Sonderfall des Cosinussignals ist jetzt das Abtasttheorem erfüllt und es gilt: |
| − | :$$y_1(t) = x_1(t) | + | :$$y_1(t) = x_1(t) ⇒ A_1 \; \underline{=2 \ \text{V}} \text{ und }\varphi_1 \; \underline{= 0}.$$ |
| − | Dieses Ergebnis soll nun noch mathematisch hergeleitet werden, wobei im Hinblick auf die noch anstehenden Teilaufgaben bereits auch eine Phase $\varphi$ im Eingangssignal berücksichtigt wird: | + | |
| + | Dieses Ergebnis soll nun noch mathematisch hergeleitet werden, wobei im Hinblick auf die noch anstehenden Teilaufgaben bereits auch eine Phase $\varphi$ im Eingangssignal berücksichtigt wird: | ||
:$$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) | :$$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Dann gilt für die Spektralfunktion, die in der oberen Grafik skizziert ist: | + | *Dann gilt für die Spektralfunktion, die in der oberen Grafik skizziert ist: |
:$$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} | :$$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} | ||
\cdot \hspace{0.05cm} \varphi} \cdot \delta | \cdot \hspace{0.05cm} \varphi} \cdot \delta | ||
| Zeile 97: | Zeile 99: | ||
\cdot \hspace{0.05cm} \varphi} \cdot \delta | \cdot \hspace{0.05cm} \varphi} \cdot \delta | ||
(f- f_{\rm 0} )\hspace{0.05cm}.$$ | (f- f_{\rm 0} )\hspace{0.05cm}.$$ | ||
| − | Mit den Abkürzungen | + | *Mit den Abkürzungen |
:$$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} | :$$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} | ||
\cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot | \cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot | ||
\hspace{0.05cm} \sin(\varphi)$$ | \hspace{0.05cm} \sin(\varphi)$$ | ||
| − | kann hierfür auch geschrieben werden: | + | :kann hierfür auch geschrieben werden: |
:$$X(f) = (R + {\rm j} \cdot I) \cdot \delta | :$$X(f) = (R + {\rm j} \cdot I) \cdot \delta | ||
(f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta | (f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta | ||
(f- f_{\rm 0} )\hspace{0.05cm}.$$ | (f- f_{\rm 0} )\hspace{0.05cm}.$$ | ||
| − | Das Spektrum des mit $f_{\rm A} = 2f_0$ abgetasteten Signals $x_{\rm A}(t)$ lautet somit: | + | *Das Spektrum des mit $f_{\rm A} = 2f_0$ abgetasteten Signals $x_{\rm A}(t)$ lautet somit: |
:$$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} | :$$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} | ||
)= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0} | )= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0} | ||
)\hspace{0.05cm}.$$ | )\hspace{0.05cm}.$$ | ||
| − | *Die untere Grafik zeigt, dass $X_{\rm A}(f)$ aus Diracfunktionen bei $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, usw. besteht. | + | :*Die untere Grafik zeigt, dass $X_{\rm A}(f)$ aus Diracfunktionen bei $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, usw. besteht. |
| − | *Alle Gewichte sind rein reell und gleich $2 \cdot R$. | + | :*Alle Gewichte sind rein reell und gleich $2 \cdot R$. |
| − | *Die Imaginärteile des periodisch fortgesetzten Spektrums heben sich auf. | + | :*Die Imaginärteile des periodisch fortgesetzten Spektrums heben sich auf. |
| + | *Berücksichtigt man weiter den rechteckförmigen Tiefpass, dessen Grenzfrequenz exakt bei $f_{\rm G} = f_0$ liegt, sowie $H(f_{\rm G}) = 0.5$, so erhält man für das Spektrum nach der Signalrekonstruktion: | ||
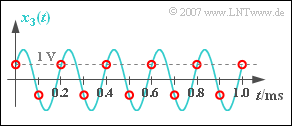
| + | [[Datei:P_ID1131__Sig_Z_5_1_d.png|right|frame|Rekonstruktion des abgetasteten Sinussignals]] | ||
| − | |||
:$$Y(f) = R \cdot \delta | :$$Y(f) = R \cdot \delta | ||
(f+ f_{\rm 0} ) + R \cdot \delta | (f+ f_{\rm 0} ) + R \cdot \delta | ||
(f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} | (f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} | ||
\cos(\varphi)\hspace{0.05cm}.$$ | \cos(\varphi)\hspace{0.05cm}.$$ | ||
| − | Die Fourierrücktransformation führt auf | + | |
| + | *Die Fourierrücktransformation führt auf | ||
:$$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) | :$$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *Es ergibt sich also unabhängig von der Eingangsphase $\varphi$ ein cosinusförmiger Verlauf. | + | |
| − | *Ist $\varphi = 0$ wie beim Signal $x_1(t)$, so ist auch die Amplitude des Ausgangssignals gleich $A$. | + | *Es ergibt sich also unabhängig von der Eingangsphase $\varphi$ ein cosinusförmiger Verlauf. |
| + | *Ist $\varphi = 0$ wie beim Signal $x_1(t)$, so ist auch die Amplitude des Ausgangssignals gleich $A$. | ||
| + | |||
| − | + | '''(4)''' Das Sinussignal hat die Phase $90^\circ$. | |
| − | '''(4)''' Das Sinussignal hat die Phase $90^\circ$. Daraus folgt direkt $y_2(t) = 0$ ⇒ Amplitude $\underline{A_2 = 0}$. | + | *Daraus folgt direkt $y_2(t) = 0$ ⇒ Amplitude $\underline{A_2 = 0}$. |
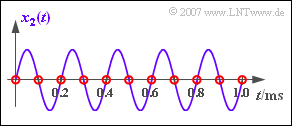
| + | [[Datei:P_ID1133__Sig_Z_5_1_e.png|right|frame|Rekonstruktion einer harmonischen Schwingung mit $60^\circ$ Phase]] | ||
*Dieses Ergebnis wird verständlich, wenn man sich die Abtastwerte in der Grafik betrachtet. | *Dieses Ergebnis wird verständlich, wenn man sich die Abtastwerte in der Grafik betrachtet. | ||
| − | *Alle Abtastwerte (rote Kreise) sind | + | *Alle Abtastwerte (rote Kreise) sind Null, so dass auch nach dem Filter kein Signal vorhanden sein kann. |
| − | + | ||
| − | + | ||
| − | '''(5)''' Trotz $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ auch das rekonstruierte Signal $y_3(t)$ ist cosinusförmig. Die Amplitude ist gleich | + | '''(5)''' Trotz $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ auch das rekonstruierte Signal $y_3(t)$ ist cosinusförmig. Die Amplitude ist gleich |
:$$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} | :$$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Aktuelle Version vom 13. Mai 2021, 15:15 Uhr
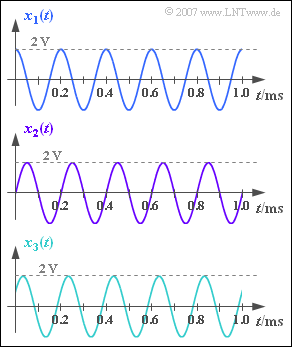
Wir betrachten drei harmonische Schwingungen mit gleicher Frequenz und gleicher Amplitude:
- $$x_1(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_2(t) = A \cdot \sin (2 \pi \cdot f_0 \cdot t) \hspace{0.05cm}, $$
- $$ x_3(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - 60^{\circ}) \hspace{0.05cm}.$$
Die Schwingungsparameter $f_0$ und $A$ können Sie der Grafik entnehnen.
Angenommen wird, dass die Signale äquidistant zu den Zeitpunkten $\nu \cdot T_{\rm A}$ abgetastet werden, wobei die Parameterwerte $T_{\rm A} = 80 \ µ \text{s}$ und $T_{\rm A} = 100 \ µ \text{s}$ analysiert werden sollen.
Die Signalrekonstruktion beim Empfänger erfolgt durch einen Tiefpass $H(f)$, der aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ das Ausgangssignal $y(t)$ formt. Es gelte:
- $$H(f) = \left\{ \begin{array}{c} 1 \\ 0.5 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_{\rm G} \hspace{0.05cm}, \\ |f| = f_{\rm G} \hspace{0.05cm}, \\ |f| > f_{\rm G} \hspace{0.05cm}, \\ \end{array}$$
Hierbei gibt $f_{\rm G}$ die Grenzfrequenz des rechteckförmigen Tiefpassfilters an. Für diese soll gelten:
- $$f_{\rm G} = \frac{1}{ 2 \cdot T_{\rm A}}\hspace{0.05cm}.$$
Das Abtasttheorem ist erfüllt, wenn $y(t) = x(t)$ gilt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Zeitdiskrete Signaldarstellung.
- Zu der hier behandelten Thematik gibt es ein interaktives Applet: Abtastung analoger Signale und Signalrekonstruktion
Fragebogen
Musterlösung
- Daraus ergibt sich die Signalfrequenz $f_0 = 1/T_0 \; \underline{= 5 \ \text{kHz}}$.
(2) Richtig sind alle Löungsvorschläge:
- Die Abtastrate beträgt hier $f_{\rm A} = 1/T_{\rm A} = 12.5 \ \text{kHz}$.
- Dieser Wert ist größer als $2 \cdot f_0 = 10 \ \text{kHz}$.
- Damit ist das Abtasttheorem unabhängig von der Phase erfüllt, und es gilt stets $y(t) = x(t)$.
(3) Die Abtastrate beträgt nun $f_{\rm A} = 2 \cdot f_0 = 10 \ \text{kHz}$.
- Nur im Sonderfall des Cosinussignals ist jetzt das Abtasttheorem erfüllt und es gilt:
- $$y_1(t) = x_1(t) ⇒ A_1 \; \underline{=2 \ \text{V}} \text{ und }\varphi_1 \; \underline{= 0}.$$
Dieses Ergebnis soll nun noch mathematisch hergeleitet werden, wobei im Hinblick auf die noch anstehenden Teilaufgaben bereits auch eine Phase $\varphi$ im Eingangssignal berücksichtigt wird:
- $$x(t) = A \cdot \cos (2 \pi \cdot f_0 \cdot t - \varphi) \hspace{0.05cm}.$$
- Dann gilt für die Spektralfunktion, die in der oberen Grafik skizziert ist:
- $$X(f) = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f+ f_{\rm 0} ) + {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
- Mit den Abkürzungen
- $$R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi) \hspace{0.5cm}{\rm und} \hspace{0.5cm}I ={A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \sin(\varphi)$$
- kann hierfür auch geschrieben werden:
- $$X(f) = (R + {\rm j} \cdot I) \cdot \delta (f+ f_{\rm 0} ) + (R - {\rm j} \cdot I) \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}.$$
- Das Spektrum des mit $f_{\rm A} = 2f_0$ abgetasteten Signals $x_{\rm A}(t)$ lautet somit:
- $$X_{\rm A}(f) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A}
)= \sum_{\mu = - \infty }^{+\infty} X (f- 2\mu \cdot f_{\rm 0}
)\hspace{0.05cm}.$$
- Die untere Grafik zeigt, dass $X_{\rm A}(f)$ aus Diracfunktionen bei $\pm f_0$, $\pm 3f_0$, $\pm 5f_0$, usw. besteht.
- Alle Gewichte sind rein reell und gleich $2 \cdot R$.
- Die Imaginärteile des periodisch fortgesetzten Spektrums heben sich auf.
- Berücksichtigt man weiter den rechteckförmigen Tiefpass, dessen Grenzfrequenz exakt bei $f_{\rm G} = f_0$ liegt, sowie $H(f_{\rm G}) = 0.5$, so erhält man für das Spektrum nach der Signalrekonstruktion:
- $$Y(f) = R \cdot \delta (f+ f_{\rm 0} ) + R \cdot \delta (f- f_{\rm 0} )\hspace{0.05cm}, \hspace{0.5cm} R = {A}/{2} \hspace{0.05cm} \cdot \hspace{0.05cm} \cos(\varphi)\hspace{0.05cm}.$$
- Die Fourierrücktransformation führt auf
- $$y(t) = A \cdot \cos (\varphi)\cdot \cos (2 \pi \cdot f_0 \cdot t ) \hspace{0.05cm}.$$
- Es ergibt sich also unabhängig von der Eingangsphase $\varphi$ ein cosinusförmiger Verlauf.
- Ist $\varphi = 0$ wie beim Signal $x_1(t)$, so ist auch die Amplitude des Ausgangssignals gleich $A$.
(4) Das Sinussignal hat die Phase $90^\circ$.
- Daraus folgt direkt $y_2(t) = 0$ ⇒ Amplitude $\underline{A_2 = 0}$.
- Dieses Ergebnis wird verständlich, wenn man sich die Abtastwerte in der Grafik betrachtet.
- Alle Abtastwerte (rote Kreise) sind Null, so dass auch nach dem Filter kein Signal vorhanden sein kann.
(5) Trotz $\varphi = 60^\circ$ gilt $\varphi_3 = 0$ ⇒ auch das rekonstruierte Signal $y_3(t)$ ist cosinusförmig. Die Amplitude ist gleich
- $$A_3 = A \cdot \cos (60^{\circ})= {A}/{2} \hspace{0.15 cm}\underline{= 1\,{\rm V}} \hspace{0.05cm}.$$
- Wenn Sie die rot eingezeichneten Abtastwerte in der Grafik betrachten, so werden Sie zugeben, dass Sie als „Signalrekonstrukteur” keine andere Entscheidung treffen würden als der Tiefpass.
- Sie kennen ja den türkisfarbenen Verlauf nicht.