Stochastische Signaltheorie/Zweidimensionale Zufallsgrößen: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
== # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL # == | == # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL # == | ||
<br> | <br> | ||
| − | Nun werden Zufallsgrößen mit statistischen Bindungen behandelt und anhand typischer Beispiele verdeutlicht. Nach der allgemeinen Beschreibung zweidimensionaler Zufallsgrößen wenden wir uns der Autokorrelationsfunktion (AKF), der Kreuzkorrelationsfunktion (KKF) | + | Nun werden Zufallsgrößen mit statistischen Bindungen behandelt und anhand typischer Beispiele verdeutlicht. |
| + | |||
| + | Nach der allgemeinen Beschreibung zweidimensionaler Zufallsgrößen wenden wir uns folgenden Beschreibungsgrößen zu: | ||
| + | |||
| + | #der Autokorrelationsfunktion (AKF), | ||
| + | #der Kreuzkorrelationsfunktion (KKF), | ||
| + | #den zugehörigen Spektralfunktionen (Leistungsdichtespektrum, Kreuzleistungsdichtespektrum). | ||
| + | |||
Im Einzelnen werden behandelt: | Im Einzelnen werden behandelt: | ||
| − | *die statistische Beschreibung von | + | *die statistische Beschreibung von »2D–Zufallsgrößen« mit Hilfe der Verbund–WDF, |
| − | *der Unterschied zwischen | + | *der Unterschied zwischen »statistischer Abhängigkeit« und »Korrelation«, |
| − | *die Klassifizierungsmerkmale | + | *die Klassifizierungsmerkmale »Stationarität« und »Ergodizität« stochastischer Prozesse, |
| − | * die Definitionen von | + | * die Definitionen von »Autokorrelationsfunktion« $\rm (AKF)$ und »Leistungsdichtespektrum« $\rm (LDS)$, |
| − | *die Definitionen von | + | *die Definitionen von »Kreuzkorrelationsfunktion« und »Kreuzleistungsdichtespektrum«, |
*die numerische Ermittlung all dieser Größen im zwei– und mehrdimensionalen Fall. | *die numerische Ermittlung all dieser Größen im zwei– und mehrdimensionalen Fall. | ||
| Zeile 36: | Zeile 43: | ||
==Eigenschaften und Beispiele== | ==Eigenschaften und Beispiele== | ||
<br> | <br> | ||
| − | Als Überleitung zu den [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Korrelationsfunktionen]] betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen. Jede der beiden Zufallsgrößen kann für sich alleine beschrieben werden mit den eingeführten Kenngrößen | + | Als Überleitung zu den [[Stochastische_Signaltheorie/Autokorrelationsfunktion_(AKF)|Korrelationsfunktionen]] betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen. |
| + | |||
| + | Jede der beiden Zufallsgrößen kann für sich alleine beschrieben werden mit den eingeführten Kenngrößen | ||
*entsprechend dem zweiten Hauptkapitel ⇒ [[Stochastische_Signaltheorie/Vom_Zufallsexperiment_zur_Zufallsgröße#.23_.C3.9CBERBLICK_ZUM_ZWEITEN_HAUPTKAPITEL_.23|Diskrete Zufallsgrößen]] | *entsprechend dem zweiten Hauptkapitel ⇒ [[Stochastische_Signaltheorie/Vom_Zufallsexperiment_zur_Zufallsgröße#.23_.C3.9CBERBLICK_ZUM_ZWEITEN_HAUPTKAPITEL_.23|Diskrete Zufallsgrößen]] | ||
*bzw. dem dritten Hauptkapitel ⇒ [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion#.23_.C3.9CBERBLICK_ZUM_DRITTEN_HAUPTKAPITEL_.23|Kontinuierliche Zufallsgrößen]]. | *bzw. dem dritten Hauptkapitel ⇒ [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion#.23_.C3.9CBERBLICK_ZUM_DRITTEN_HAUPTKAPITEL_.23|Kontinuierliche Zufallsgrößen]]. | ||
| Zeile 42: | Zeile 51: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer '''zweidimensionalen Zufallsgröße''' $(x, y)$ zusammenzufassen. | + | $\text{Definition:}$ Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer '''zweidimensionalen Zufallsgröße''' $(x, y)$ zusammenzufassen. |
*Die Einzelkomponenten können Signale sein wie der Real– und Imaginärteil eines phasenmodulierten Signals. | *Die Einzelkomponenten können Signale sein wie der Real– und Imaginärteil eines phasenmodulierten Signals. | ||
| − | *Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D–Zufallsgrößen, wie das folgende Beispiel zeigen soll.}} | + | *Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D–Zufallsgrößen, wie das folgende Beispiel zeigen soll.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 1:}$ Das linke Diagramm stammt von dem Zufallsexperiment „Werfen mit zwei Würfeln”. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen: | + | $\text{Beispiel 1:}$ Das linke Diagramm stammt von dem Zufallsexperiment „Werfen mit zwei Würfeln”. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen: |
| − | |||
| − | |||
| − | |||
[[Datei: P_ID162__Sto_T_4_1_S1_neu.png |frame| Zwei Beispiele statistisch abhängiger Zufallsgrößen]] | [[Datei: P_ID162__Sto_T_4_1_S1_neu.png |frame| Zwei Beispiele statistisch abhängiger Zufallsgrößen]] | ||
| + | *Ist $W_1 = 1$, so kann $S$ nur Werte zwischen $2$ und $7$ annehmen und zwar mit jeweils gleicher Warscheinlichkeit. | ||
| + | *Dagegen sind bei $W_1 = 6$ für $S$ alle Werte zwischen $7$ und $12$ möglich, ebenfalls mit gleicher Warscheinlichkeit. | ||
| − | In der rechten Grafik sind die Maximaltemperaturen der $31$ Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich: | + | In der rechten Grafik sind die Maximaltemperaturen der $31$ Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich: |
| − | *Obwohl die Messpunkte etwa $\text{100 km}$ auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen $($knapp $3000$ gegenüber $520$ Meter$)$ im Mittel um etwa $20$ Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Zufallsgrößen ${\it Θ}_{\rm M}$ und ${\it Θ}_{\rm Z}$. | + | *Obwohl die Messpunkte etwa $\text{100 km}$ auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen $($knapp $3000$ gegenüber $520$ Meter$)$ im Mittel um etwa $20$ Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Zufallsgrößen ${\it Θ}_{\rm M}$ und ${\it Θ}_{\rm Z}$. |
| − | *Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze. }} | + | *Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze. }} |
==Verbundwahrscheinlichkeitsdichtefunktion== | ==Verbundwahrscheinlichkeitsdichtefunktion== | ||
<br> | <br> | ||
| − | Wir beschränken uns hier meist auf kontinuierliche Zufallsgrößen. Manchmal wird jedoch auch auf die Besonderheiten zweidimensionaler diskreter Zufallsgrößen genauer eingegangen. Die meisten der vorher für eindimensionale Zufallsgrößen definierten Kenngrößen kann man problemlos auf zweidimensionale Größen erweitern. | + | Wir beschränken uns hier meist auf kontinuierliche Zufallsgrößen. |
| + | *Manchmal wird jedoch auch auf die Besonderheiten zweidimensionaler diskreter Zufallsgrößen genauer eingegangen. | ||
| + | *Die meisten der vorher für eindimensionale Zufallsgrößen definierten Kenngrößen kann man problemlos auf zweidimensionale Größen erweitern. | ||
| + | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| Zeile 70: | Zeile 81: | ||
$\rm Hinweis$: | $\rm Hinweis$: | ||
*Ist die 2D–Zufallsgröße diskret, so muss die Definition geringfügig modifiziert werden: | *Ist die 2D–Zufallsgröße diskret, so muss die Definition geringfügig modifiziert werden: | ||
| − | *Bei den | + | *Bei den unteren Bereichsgrenzen ist dann gemäß der Seite [[Stochastische_Signaltheorie/Verteilungsfunktion#Verteilungsfunktion_bei_diskreten_Zufallsgr.C3.B6.C3.9Fen|Verteilungsfunktion bei diskreten Zufallsgrößen]] das „≤”–Zeichen durch das „<”–Zeichen zu ersetzen.}} |
| Zeile 89: | Zeile 100: | ||
| − | Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der 1D-VTF und der 2D-VTF: | + | Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der "1D-VTF" und der "2D-VTF": |
| − | *Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt: | + | *Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt: |
:$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$ | :$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$ | ||
*Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{x}$ und $r_{y}$ angeben: | *Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{x}$ und $r_{y}$ angeben: | ||
| Zeile 115: | Zeile 126: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Daraus folgt, dass bei '''statistischer Unabhängigkeit''' folgende Bedingung bezüglich der 2D–Wahrscheinlichkeitsdichtefunktion erfüllt sein muss: | + | $\text{Definition:}$ Daraus folgt, dass bei '''statistischer Unabhängigkeit''' folgende Bedingung bezüglich der 2D–Wahrscheinlichkeitsdichtefunktion erfüllt sein muss: |
:$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$}} | :$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$}} | ||
| Zeile 123: | Zeile 134: | ||
*Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der 2D–WDF $f_{xy}(x, y)$. | *Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der 2D–WDF $f_{xy}(x, y)$. | ||
*Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile. | *Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile. | ||
| − | |||
[[Datei:P_ID153__Sto_T_4_1_S4_nochmals_neu.png |frame| Statistisch unabhängige Komponenten: $f_{xy}(x,y)$, $f_{x}(x)$ und $f_{y}(y)$]] | [[Datei:P_ID153__Sto_T_4_1_S4_nochmals_neu.png |frame| Statistisch unabhängige Komponenten: $f_{xy}(x,y)$, $f_{x}(x)$ und $f_{y}(y)$]] | ||
| − | Die Grafik kann wie folgt interpretiert werden: | + | <br>Die Grafik kann wie folgt interpretiert werden: |
| − | *Die Randwahrscheinlichkeitsdichten $f_{x}(x)$ und $f_{y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist. | + | *Die Randwahrscheinlichkeitsdichten $f_{x}(x)$ und $f_{y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist. |
*$f_{x}(x)$ und $f_{y}(y)$ liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen bestehen oder nicht. | *$f_{x}(x)$ und $f_{y}(y)$ liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen bestehen oder nicht. | ||
| − | *Anhand der 2D-WDF $f_{xy}(x,y)$ erkennt man aber, dass es hier zwischen den beiden Komponenten $x$ und $y$ keine statistischen Bindungen gibt. | + | *Anhand der 2D-WDF $f_{xy}(x,y)$ erkennt man aber, dass es hier zwischen den beiden Komponenten $x$ und $y$ keine statistischen Bindungen gibt. |
| − | *Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Rand–WDF $f_{y}(y)$ ist. Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{x}(x)$. | + | *Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Rand–WDF $f_{y}(y)$ ist. Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{x}(x)$. |
| − | + | *Diese Tatsache ist gleichbedeutend mit der Aussage, dass in diesem Beispiel $f_{xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann: | |
| − | *Diese Tatsache ist gleichbedeutend mit der Aussage, dass in diesem Beispiel $f_{xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann: $f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$}} | + | :$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$}} |
==WDF und VTF bei statistisch abhängigen Komponenten== | ==WDF und VTF bei statistisch abhängigen Komponenten== | ||
| Zeile 147: | Zeile 157: | ||
Man erkennt aus dieser Darstellung: | Man erkennt aus dieser Darstellung: | ||
| − | + | #Die Integration über $f_{xy}(x, y)$ parallel zur $x$–Achse führt zur dreieckförmigen Randdichte $f_{y}(y)$, die Integration parallel zur $y$–Achse zur trapezförmigen WDF $f_{x}(x)$. | |
| − | + | #Aus der 2D-WDF $f_{xy}(x, y)$ ist bereits zu erahnen, dass für jeden $x$–Wert im statistischen Mittel ein anderer $y$–Wert zu erwarten ist. | |
| − | + | #Das bedeutet, dass hier die Komponenten $x$ und $y$ statistisch voneinander abhängen. }} | |
==Erwartungswerte zweidimensionaler Zufallsgrößen== | ==Erwartungswerte zweidimensionaler Zufallsgrößen== | ||
<br> | <br> | ||
| − | Ein Sonderfall der statistischen Abhängigkeit ist die | + | Ein Sonderfall der statistischen Abhängigkeit ist die "Korrelation". |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Unter '''Korrelation''' versteht man eine | + | $\text{Definition:}$ Unter '''Korrelation''' versteht man eine "lineare Abhängigkeit" zwischen den Einzelkomponenten $x$ und $y$. |
*Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig. | *Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig. | ||
*Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.}} | *Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.}} | ||
| Zeile 171: | Zeile 181: | ||
$\text{Definition:}$ Für die (nichtzentrierten) '''Momente''' gilt die Beziehung: | $\text{Definition:}$ Für die (nichtzentrierten) '''Momente''' gilt die Beziehung: | ||
:$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$ | :$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$ | ||
| − | Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$ }} | + | Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$ }} |
| Zeile 181: | Zeile 191: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Besondere Bedeutung besitzt die '''Kovarianz''' $(k = l = 1)$, die ein Maß für die | + | $\text{Definition:}$ Besondere Bedeutung besitzt die '''Kovarianz''' $(k = l = 1)$, die ein Maß für die lineare statistische Abhängigkeit zwischen den Zufallsgrößen $x$ und $y$ ist: |
:$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$ | :$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$ | ||
| − | Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht.}} | + | Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht.}} |
''Anmerkungen:'' | ''Anmerkungen:'' | ||
| − | *Die Kovarianz $\mu_{11}=\mu_{xy}$ hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen: | + | *Die Kovarianz $\mu_{11}=\mu_{xy}$ hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen: |
:$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$ | :$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$ | ||
| + | *Diese Gleichung ist für numerische Auswertungen enorm vorteilhaft, da $m_{xy}$, $m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ in einem einzigen Durchlauf gefunden werden können. | ||
| + | *Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und könnte dann erst in einem zweiten Durchlauf den Erwartungswert ${\rm E}\big[(x - m_x) · (y - m_y)\big]$ berechnen. | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Beispiel 4:}$ In den beiden ersten Zeilen der Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben. | $\text{Beispiel 4:}$ In den beiden ersten Zeilen der Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben. | ||
| − | + | [[Datei:P_ID628__Sto_T_4_1_S6Neu.png |right|frame| Beispielhafte 2D-Erwartungswerte]] | |
| − | *Durch Mittelung über | + | *Durch Mittelung über jeweils zehn Folgenelemente erhält man |
:$$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$ | :$$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$ | ||
*Daraus ergibt sich direkt der Wert für die Kovarianz: | *Daraus ergibt sich direkt der Wert für die Kovarianz: | ||
| Zeile 207: | Zeile 215: | ||
==Korrelationskoeffizient== | ==Korrelationskoeffizient== | ||
<br> | <br> | ||
| − | Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten|WDF und VTF bei statistisch unabhängigen Komponenten]] betrachtet. | + | Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten|WDF und VTF bei statistisch unabhängigen Komponenten]] betrachtet. |
| − | *Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also | + | *Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind. |
| − | *Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$ | + | *Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$ |
| − | Man spricht von & | + | Man spricht von '''vollständiger Korrelation''', wenn die (deterministische) Abhängigkeit zwischen $x$ und $y$ durch die Gleichung $y = K · x$ ausgedrückt wird. Dann ergibt sich für die Kovarianz: |
| − | * $\mu_{xy} = σ_x · σ_y$ bei positivem | + | * $\mu_{xy} = σ_x · σ_y$ bei positivem $K$–Wert, |
| − | * $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert. | + | * $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert. |
| Zeile 221: | Zeile 229: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Der '''Korrelationskoeffizient''' ist der | + | $\text{Definition:}$ Der '''Korrelationskoeffizient''' ist der Quotient aus der Kovarianz $\mu_{xy}$ und dem Produkt der Effektivwerte $σ_x$ und $σ_y$ der beiden Komponenten: |
:$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$}} | :$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$}} | ||
| − | Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf: | + | Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf: |
| − | *Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$. | + | *Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$. |
| − | *Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$. | + | *Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$. |
| − | *Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$ ⇒ vollständige Korrelation. | + | *Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$ ⇒ vollständige Korrelation. |
| − | *Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$. | + | *Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$. |
| − | *Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird. | + | *Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird. |
| − | [[Datei:P_ID232__Sto_T_4_1_S7a_neu.png |right|frame| Gaußsche 2D-WDF mit Korrelation]] | + | {{GraueBox|TEXT= |
| − | + | [[Datei:P_ID232__Sto_T_4_1_S7a_neu.png |right|frame| Gaußsche 2D-WDF mit Korrelation]] | |
$\text{Beispiel 5:}$ Es gelten folgende Voraussetzungen: | $\text{Beispiel 5:}$ Es gelten folgende Voraussetzungen: | ||
| − | *Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF. | + | *Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF. |
| − | *Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$. | + | *Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$. |
| − | *Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$. | + | *Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$. |
| − | Im Unterschied zum [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten| Beispiel 2]] mit statistisch unabhängigen Komponenten ⇒ $ρ_{xy} = 0$ (trotz $σ_y < σ_x$ | + | Im Unterschied zum [[Stochastische_Signaltheorie/Zweidimensionale_Zufallsgrößen#WDF_und_VTF_bei_statistisch_unabh.C3.A4ngigen_Komponenten| Beispiel 2]] mit statistisch unabhängigen Komponenten ⇒ $ρ_{xy} = 0$ $($trotz $σ_y < σ_x)$ erkennt man, dass hier bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.}} |
| − | == | + | ==Regressionsgerade== |
<br> | <br> | ||
| − | + | {{BlaueBox|TEXT= | |
[[Datei: P_ID1089__Sto_T_4_1_S7b_neu.png |frame| Gaußsche 2D-WDF mit Korrelationsgerade]] | [[Datei: P_ID1089__Sto_T_4_1_S7b_neu.png |frame| Gaußsche 2D-WDF mit Korrelationsgerade]] | ||
| − | + | ||
| − | $\text{Definition:}$ Als ''' | + | $\text{Definition:}$ Als '''Regressionsgerade''' bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch "Korrelationsgerade" genannt. |
| − | Die | + | Die Regressionsgerade besitzt folgende Eigenschaften: |
| − | *Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal: | + | *Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal: |
:$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$ | :$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$ | ||
| − | *Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet: | + | *Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet: |
| − | :$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$}} | + | :$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$ |
| − | + | *Der Winkel, den die Regressionsgerade zur $x$–Achse einnimmt, beträgt: | |
| + | :$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$}} | ||
| − | |||
| − | |||
| − | Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt. | + | Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt. |
| − | *Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung. | + | *Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung. |
| − | *Das interaktive Applet [[Applets: | + | *Das interaktive Applet [[Applets:Korrelation_und_Regressionsgerade]] verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird: |
| − | :$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}(\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$ | + | :$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$ |
Aktuelle Version vom 24. Januar 2022, 14:01 Uhr
Inhaltsverzeichnis
- 1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
- 2 Eigenschaften und Beispiele
- 3 Verbundwahrscheinlichkeitsdichtefunktion
- 4 Zweidimensionale Verteilungsfunktion
- 5 WDF und VTF bei statistisch unabhängigen Komponenten
- 6 WDF und VTF bei statistisch abhängigen Komponenten
- 7 Erwartungswerte zweidimensionaler Zufallsgrößen
- 8 Korrelationskoeffizient
- 9 Regressionsgerade
- 10 Aufgaben zum Kapitel
# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
Nun werden Zufallsgrößen mit statistischen Bindungen behandelt und anhand typischer Beispiele verdeutlicht.
Nach der allgemeinen Beschreibung zweidimensionaler Zufallsgrößen wenden wir uns folgenden Beschreibungsgrößen zu:
- der Autokorrelationsfunktion (AKF),
- der Kreuzkorrelationsfunktion (KKF),
- den zugehörigen Spektralfunktionen (Leistungsdichtespektrum, Kreuzleistungsdichtespektrum).
Im Einzelnen werden behandelt:
- die statistische Beschreibung von »2D–Zufallsgrößen« mit Hilfe der Verbund–WDF,
- der Unterschied zwischen »statistischer Abhängigkeit« und »Korrelation«,
- die Klassifizierungsmerkmale »Stationarität« und »Ergodizität« stochastischer Prozesse,
- die Definitionen von »Autokorrelationsfunktion« $\rm (AKF)$ und »Leistungsdichtespektrum« $\rm (LDS)$,
- die Definitionen von »Kreuzkorrelationsfunktion« und »Kreuzleistungsdichtespektrum«,
- die numerische Ermittlung all dieser Größen im zwei– und mehrdimensionalen Fall.
Weitere Informationen zum Thema „Zweidimensionale Zufallsgrößen” sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Kapitel 5: Zweidimensionale Zufallsgrößen (Programm „zwd”)
- Kapitel 9: Stochastische Prozesse (Programm „sto”)
des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP–Version des Programms,
- der Praktikumsanleitung – Teil A ⇒ Link verweist auf die PDF–Version mit Kapitel 5: Seite 81-97,
- der Praktikumsanleitung – Teil B ⇒ Link verweist auf die PDF–Version mit Kapitel 9: Seite 207-228.
Eigenschaften und Beispiele
Als Überleitung zu den Korrelationsfunktionen betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen.
Jede der beiden Zufallsgrößen kann für sich alleine beschrieben werden mit den eingeführten Kenngrößen
- entsprechend dem zweiten Hauptkapitel ⇒ Diskrete Zufallsgrößen
- bzw. dem dritten Hauptkapitel ⇒ Kontinuierliche Zufallsgrößen.
$\text{Definition:}$ Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $(x, y)$ zusammenzufassen.
- Die Einzelkomponenten können Signale sein wie der Real– und Imaginärteil eines phasenmodulierten Signals.
- Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D–Zufallsgrößen, wie das folgende Beispiel zeigen soll.
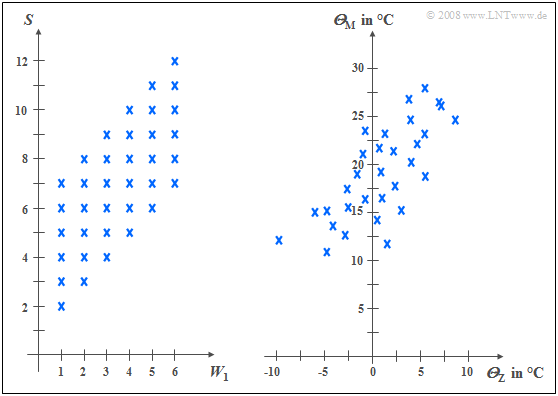
$\text{Beispiel 1:}$ Das linke Diagramm stammt von dem Zufallsexperiment „Werfen mit zwei Würfeln”. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen:
- Ist $W_1 = 1$, so kann $S$ nur Werte zwischen $2$ und $7$ annehmen und zwar mit jeweils gleicher Warscheinlichkeit.
- Dagegen sind bei $W_1 = 6$ für $S$ alle Werte zwischen $7$ und $12$ möglich, ebenfalls mit gleicher Warscheinlichkeit.
In der rechten Grafik sind die Maximaltemperaturen der $31$ Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich:
- Obwohl die Messpunkte etwa $\text{100 km}$ auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen $($knapp $3000$ gegenüber $520$ Meter$)$ im Mittel um etwa $20$ Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Zufallsgrößen ${\it Θ}_{\rm M}$ und ${\it Θ}_{\rm Z}$.
- Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze.
Verbundwahrscheinlichkeitsdichtefunktion
Wir beschränken uns hier meist auf kontinuierliche Zufallsgrößen.
- Manchmal wird jedoch auch auf die Besonderheiten zweidimensionaler diskreter Zufallsgrößen genauer eingegangen.
- Die meisten der vorher für eindimensionale Zufallsgrößen definierten Kenngrößen kann man problemlos auf zweidimensionale Größen erweitern.
$\text{Definition:}$ Die Wahrscheinlichkeitsdichtefunktion der zweidimensionalen Zufallsgröße an der Stelle $(x_\mu, y_\mu)$ ⇒ Verbundwahrscheinlichkeitsdichtefunktion ist eine Erweiterung der eindimensionalen WDF $(∩$ kennzeichnet die logische UND-Verknüpfung$)$:
- $$f_{xy}(x_\mu, \hspace{0.1cm}y_\mu) = \lim_{\left.{\Delta x\rightarrow 0 \atop {\Delta y\rightarrow 0} }\right.}\frac{ {\rm Pr}\big [ (x_\mu - {\rm \Delta} x/{\rm 2} \le x \le x_\mu + {\rm \Delta} x/{\rm 2}) \cap (y_\mu - {\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \Delta} \ x\cdot{\rm \Delta} y}.$$
$\rm Hinweis$:
- Ist die 2D–Zufallsgröße diskret, so muss die Definition geringfügig modifiziert werden:
- Bei den unteren Bereichsgrenzen ist dann gemäß der Seite Verteilungsfunktion bei diskreten Zufallsgrößen das „≤”–Zeichen durch das „<”–Zeichen zu ersetzen.
Anhand dieser (Verbund)–WDF $f_{xy}(x, y)$ werden auch statistische Abhängigkeiten innerhalb der zweidimensionalen Zufallsgröße $(x, y)$ vollständig erfasst im Gegensatz zu den beiden eindimensionalen Dichtefunktionen ⇒ Randwahrscheinlichkeitsdichtefunktionen:
- $$f_{x}(x) = \int _{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}y ,$$
- $$f_{y}(y) = \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x .$$
Diese beiden Randdichtefunktionen $f_x(x)$ und $f_y(y)$
- liefern lediglich statistische Aussagen über die Einzelkomponenten $x$ bzw. $y$,
- nicht jedoch über die Bindungen zwischen diesen.
Zweidimensionale Verteilungsfunktion
$\text{Definition:}$ Die 2D-Verteilungsfunktion ist ebenso wie die 2D-WDF lediglich eine sinnvolle Erweiterung der eindimensionalen Verteilungsfunktion (VTF):
- $$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$
Es ergeben sich folgende Gemeinsamkeiten und Unterschiede zwischen der "1D-VTF" und der "2D-VTF":
- Der Funktionalzusammenhang zwischen zweidimensionaler WDF und zweidimensionaler VTF ist wie im eindimensionalen Fall durch die Integration gegeben, aber nun in zwei Dimensionen. Bei kontinuierlichen Zufallsgrößen gilt:
- $$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$
- Umgekehrt lässt sich die Wahrscheinlichkeitsdichtefunktion aus der Verteilungsfunktion durch partielle Differentiation nach $r_{x}$ und $r_{y}$ angeben:
- $$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$
- Bezüglich der Verteilungsfunktion $F_{xy}(r_{x}, r_{y})$ gelten folgende Grenzwerte:
- $$F_{xy}(-\infty,-\infty) = 0,$$
- $$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$
- $$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$
- $$F_{xy} (+\infty,+\infty) = 1.$$
- Im Grenzfall $($unendlich große $r_{x}$ und $r_{y})$ ergibt sich demnach für die 2D-VTF der Wert $1$. Daraus erhält man die Normierungsbedingung für die 2D-WDF:
- $$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$
$\text{Fazit:}$ Beachten Sie den signifikanten Unterschied zwischen eindimensionalen und zweidimensionalen Zufallsgrößen:
- Bei eindimensionalen Zufallsgrößen ergibt die Fläche unter der WDF stets den Wert $1$.
- Bei zweidimensionalen Zufallsgrößen ist das WDF-Volumen immer gleich $1$.
WDF und VTF bei statistisch unabhängigen Komponenten
Bei statistisch unabhängigen Komponenten $x$ und $y$ gilt für die Verbundwahrscheinlichkeit nach den elementaren Gesetzmäßigkeiten der Statistik, falls $x$ und $y$ wertkontinuierlich sind:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$
Hierfür kann bei unabhängigen Komponenten auch geschrieben werden:
- $${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$
$\text{Definition:}$ Daraus folgt, dass bei statistischer Unabhängigkeit folgende Bedingung bezüglich der 2D–Wahrscheinlichkeitsdichtefunktion erfüllt sein muss:
- $$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$
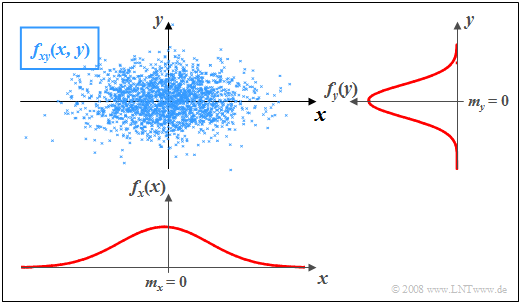
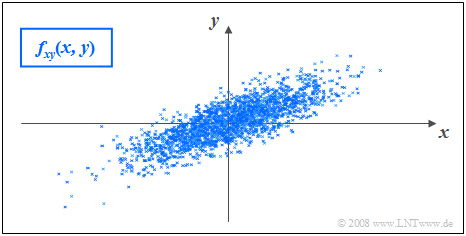
$\text{Beispiel 2:}$ In der Grafik sind die Momentanwerte einer zweidimensionalen Zufallsgröße als Punkte in der $(x, y)$–Ebene eingetragen.
- Bereiche mit vielen Punkten, die dementsprechend dunkel wirken, kennzeichnen große Werte der 2D–WDF $f_{xy}(x, y)$.
- Dagegen besitzt die Zufallsgröße $(x, y)$ in eher hellen Bereichen nur verhältnismäßig wenig Anteile.
Die Grafik kann wie folgt interpretiert werden:
- Die Randwahrscheinlichkeitsdichten $f_{x}(x)$ und $f_{y}(y)$ lassen bereits erkennen, dass sowohl $x$ als auch $y$ gaußähnlich und mittelwertfrei sind, und dass die Zufallsgröße $x$ eine größere Streuung als $y$ aufweist.
- $f_{x}(x)$ und $f_{y}(y)$ liefern jedoch keine Informationen darüber, ob bei der Zufallsgröße $(x, y)$ statistische Bindungen bestehen oder nicht.
- Anhand der 2D-WDF $f_{xy}(x,y)$ erkennt man aber, dass es hier zwischen den beiden Komponenten $x$ und $y$ keine statistischen Bindungen gibt.
- Bei statistischer Unabhängigkeit liefert jeder Schnitt durch $f_{xy}(x, y)$ parallel zur $y$-Achse eine Funktion, die formgleich mit der Rand–WDF $f_{y}(y)$ ist. Ebenso sind alle Schnitte parallel zur $x$-Achse formgleich mit $f_{x}(x)$.
- Diese Tatsache ist gleichbedeutend mit der Aussage, dass in diesem Beispiel $f_{xy}(x, y)$ als Produkt der beiden Randwahrscheinlichkeitsdichten dargestellt werden kann:
- $$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$
WDF und VTF bei statistisch abhängigen Komponenten
Bestehen statistische Bindungen zwischen $x$ und $y$, so liefern unterschiedliche Schnitte parallel zur $x$– bzw. $y$–Achse jeweils unterschiedliche, nicht formgleiche Funktionen. In diesem Fall lässt sich die Verbund–WDF natürlich auch nicht als Produkt der beiden (eindimensionalen) Randwahrscheinlichkeitsdichten beschreiben.
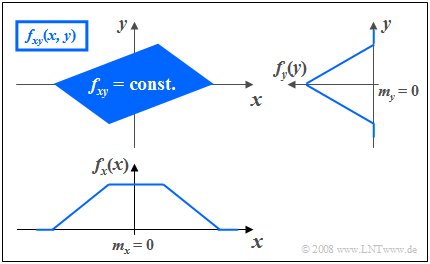
$\text{Beispiel 3:}$ Die Grafik zeigt die Momentanwerte einer zweidimensionalen Zufallsgröße in der $(x, y)$–Ebene, wobei nun im Gegensatz zum $\text{Beispiel 2}$ zwischen $x$ und $y$ statistische Bindungen bestehen.
- Die 2D–Zufallsgröße nimmt im blau eingezeichneten Parallelogramm alle 2D–Werte mit gleicher Wahrscheinlichkeit an.
- Außerhalb des Parallelogramms sind keine Werte möglich.
Man erkennt aus dieser Darstellung:
- Die Integration über $f_{xy}(x, y)$ parallel zur $x$–Achse führt zur dreieckförmigen Randdichte $f_{y}(y)$, die Integration parallel zur $y$–Achse zur trapezförmigen WDF $f_{x}(x)$.
- Aus der 2D-WDF $f_{xy}(x, y)$ ist bereits zu erahnen, dass für jeden $x$–Wert im statistischen Mittel ein anderer $y$–Wert zu erwarten ist.
- Das bedeutet, dass hier die Komponenten $x$ und $y$ statistisch voneinander abhängen.
Erwartungswerte zweidimensionaler Zufallsgrößen
Ein Sonderfall der statistischen Abhängigkeit ist die "Korrelation".
$\text{Definition:}$ Unter Korrelation versteht man eine "lineare Abhängigkeit" zwischen den Einzelkomponenten $x$ und $y$.
- Korrelierte Zufallsgrößen sind damit stets auch statistisch abhängig.
- Aber nicht jede statistische Abhängigkeit bedeutet gleichzeitig eine Korrelation.
Zur quantitativen Erfassung der Korrelation verwendet man verschiedene Erwartungswerte der 2D-Zufallsgröße $(x, y)$.
Diese sind analog definiert zum eindimensionalen Fall
- gemäß Kapitel 2 (bei wertdiskreten Zufallsgrößen)
- bzw. Kapitel 3 (bei wertkontinuierlichen Zufallsgrößen):
$\text{Definition:}$ Für die (nichtzentrierten) Momente gilt die Beziehung:
- $$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$
Die beiden linearen Mittelwerte sind somit $m_x = m_{10}$ und $m_y = m_{01}.$
$\text{Definition:}$ Die auf $m_x$ bzw. $m_y$ bezogenen Zentralmomente lauten:
- $$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$
In dieser allgemein gültigen Definitionsgleichung sind die Varianzen $σ_x^2$ und $σ_y^2$ der zwei Einzelkomponenten durch $\mu_{20}$ bzw. $\mu_{02}$ mit enthalten.
$\text{Definition:}$ Besondere Bedeutung besitzt die Kovarianz $(k = l = 1)$, die ein Maß für die lineare statistische Abhängigkeit zwischen den Zufallsgrößen $x$ und $y$ ist:
- $$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$
Im Folgenden bezeichnen wir die Kovarianz $\mu_{11}$ teilweise auch mit $\mu_{xy}$, falls sich die Kovarianz auf die Zufallsgrößen $x$ und $y$ bezieht.
Anmerkungen:
- Die Kovarianz $\mu_{11}=\mu_{xy}$ hängt wie folgt mit dem nichtzentrierten Moment $m_{11} = m_{xy} = {\rm E}\big[x · y\big]$ zusammen:
- $$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$
- Diese Gleichung ist für numerische Auswertungen enorm vorteilhaft, da $m_{xy}$, $m_x$ und $m_y$ aus den Folgen $〈x_v〉$ und $〈y_v〉$ in einem einzigen Durchlauf gefunden werden können.
- Würde man dagegen die Kovarianz $\mu_{xy}$ entsprechend der oberen Definitionsgleichung berechnen, so müsste man in einem ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln und könnte dann erst in einem zweiten Durchlauf den Erwartungswert ${\rm E}\big[(x - m_x) · (y - m_y)\big]$ berechnen.
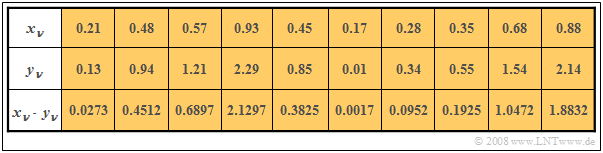
$\text{Beispiel 4:}$ In den beiden ersten Zeilen der Tabelle sind die jeweils ersten Elemente zweier Zufallsfolgen $〈x_ν〉$ und $〈y_ν〉$ eingetragen. In der letzten Zeile sind die jeweiligen Produkte $x_ν · y_ν$ angegeben.
- Durch Mittelung über jeweils zehn Folgenelemente erhält man
- $$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$
- Daraus ergibt sich direkt der Wert für die Kovarianz:
- $$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$
Ohne Kenntnis der Gleichung $\mu_{xy} = m_{xy} - m_x · m_y$ hätte man zunächst im ersten Durchlauf die Mittelwerte $m_x$ und $m_y$ ermitteln müssen,
um dann in einem zweiten Durchlauf die Kovarianz $\mu_{xy}$ als Erwartungswert des Produkts der mittelwertfreien Größen bestimmen zu können.
Korrelationskoeffizient
Bei statististischer Unabhängigkeit der beiden Komponenten $x$ und $y$ ist die Kovarianz $\mu_{xy} \equiv 0$. Dieser Fall wurde bereits im $\text{Beispiel 2}$ auf der Seite WDF und VTF bei statistisch unabhängigen Komponenten betrachtet.
- Das Ergebnis $\mu_{xy} = 0$ ist aber auch bei statistisch abhängigen Komponenten $x$ und $y$ möglich, nämlich dann, wenn diese unkorreliert, also linear unabhängig sind.
- Die statistische Abhängigkeit ist dann nicht von erster, sondern von höherer Ordnung, zum Beispiel entsprechend der Gleichung $y=x^2.$
Man spricht von vollständiger Korrelation, wenn die (deterministische) Abhängigkeit zwischen $x$ und $y$ durch die Gleichung $y = K · x$ ausgedrückt wird. Dann ergibt sich für die Kovarianz:
- $\mu_{xy} = σ_x · σ_y$ bei positivem $K$–Wert,
- $\mu_{xy} = - σ_x · σ_y$ bei negativem $K$–Wert.
Deshalb verwendet man häufig als Beschreibungsgröße anstelle der Kovarianz den so genannten Korrelationskoeffizienten.
$\text{Definition:}$ Der Korrelationskoeffizient ist der Quotient aus der Kovarianz $\mu_{xy}$ und dem Produkt der Effektivwerte $σ_x$ und $σ_y$ der beiden Komponenten:
- $$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$
Der Korrelationskoeffizient $\rho_{xy}$ weist folgende Eigenschaften auf:
- Aufgrund der Normierung gilt stets $-1 \le ρ_{xy} ≤ +1$.
- Sind die beiden Zufallsgrößen $x$ und $y$ unkorreliert, so ist $ρ_{xy} = 0$.
- Bei strenger linearer Abhängigkeit zwischen $x$ und $y$ ist $ρ_{xy}= ±1$ ⇒ vollständige Korrelation.
- Ein positiver Korrelationskoeffizient bedeutet, dass bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
- Dagegen drückt ein negativer Korrelationskoeffizient aus, dass $y$ mit steigendem $x$ im Mittel kleiner wird.
$\text{Beispiel 5:}$ Es gelten folgende Voraussetzungen:
- Die betrachteten Komponenten $x$ und $y$ besitzen jeweils eine gaußförmige WDF.
- Die beiden Streuungen sind unterschiedlich $(σ_y < σ_x)$.
- Der Korrelationskoeffizient beträgt $ρ_{xy} = 0.8$.
Im Unterschied zum Beispiel 2 mit statistisch unabhängigen Komponenten ⇒ $ρ_{xy} = 0$ $($trotz $σ_y < σ_x)$ erkennt man, dass hier bei größerem $x$–Wert im statistischen Mittel auch $y$ größer ist als bei kleinerem $x$.
Regressionsgerade
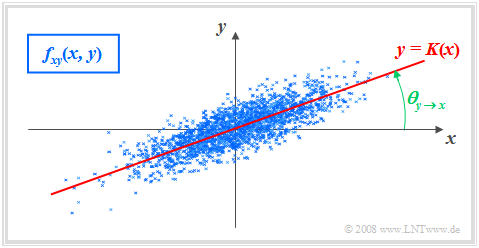
$\text{Definition:}$ Als Regressionsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch "Korrelationsgerade" genannt.
Die Regressionsgerade besitzt folgende Eigenschaften:
- Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:
- $$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$
- Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet:
- $$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$
- Der Winkel, den die Regressionsgerade zur $x$–Achse einnimmt, beträgt:
- $$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$
Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt.
- Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.
- Das interaktive Applet Korrelation und Regressionsgerade verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:
- $$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$
Aufgaben zum Kapitel
Aufgabe 4.1: Dreieckiges (x, y)-Gebiet
Aufgabe 4.1Z: Verabredung zum Frühstück
Aufgabe 4.1: Wieder Dreieckgebiet
Aufgabe 4.2Z: Korrelation zwischen $x$ und $e^x$
Aufgabe 4.3: Algebraische und Modulo-Summe
Aufgabe 4.3Z: Diracförmige 2D-WDF