Aufgaben:Aufgabe 2.7: Ist der Modulationsgrad zu groß?: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
[[Datei:P_ID1032__Mod_A_2_7.png|right|frame|Signalverläufe der „ZSB–AM mit Träger”]] | [[Datei:P_ID1032__Mod_A_2_7.png|right|frame|Signalverläufe der „ZSB–AM mit Träger”]] | ||
| − | Das cosinusförmige Quellensignal $q(t)$ mit Amplitude $A_{\rm N} = 5\ \rm V$ und Frequenz $f_{\rm N} = 1 \ \rm kHz$ wird $\rm | + | Das cosinusförmige Quellensignal $q(t)$ mit Amplitude $A_{\rm N} = 5\ \rm V$ und Frequenz $f_{\rm N} = 1 \ \rm kHz$ wird $\rm ZSB$–amplitudenmoduliert. Für das Empfangssignal gilt bei dem vorausgesetzten idealen Kanal: |
:$$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ | :$$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$ | ||
Es handelt sich folglich um eine „ZSB–AM mit Träger”. | Es handelt sich folglich um eine „ZSB–AM mit Träger”. | ||
| Zeile 12: | Zeile 12: | ||
dargestellt. Das rot gezeichnete Sinkensignal | dargestellt. Das rot gezeichnete Sinkensignal | ||
:$$v_{\rm A}(t) = a(t) - A_{\rm T}$$ | :$$v_{\rm A}(t) = a(t) - A_{\rm T}$$ | ||
| − | gehört zu einem Hüllkurvendemodulator, bei dem von der Hüllkurve $a(t)$ genau der beim Sender zugeführte Träger $(A_{\rm T})$ subtrahiert wird. | + | gehört zu einem Hüllkurvendemodulator, bei dem von der Hüllkurve $a(t)$ genau der beim Sender zugeführte Träger $(A_{\rm T})$ subtrahiert wird. |
Dieses Signal $v_{\rm A}(t)$ besitzt ebenso wie das zugehörige Fehlersignal $ε_{\rm A}(t)$ einen Gleichanteil. Aufgrund der Periodizität kann es durch die folgende Fourierreihe approximiert werden: | Dieses Signal $v_{\rm A}(t)$ besitzt ebenso wie das zugehörige Fehlersignal $ε_{\rm A}(t)$ einen Gleichanteil. Aufgrund der Periodizität kann es durch die folgende Fourierreihe approximiert werden: | ||
:$$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm mit}$$ | :$$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm mit}$$ | ||
| − | :$$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ | + | ::$$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$ |
| − | :$$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ | + | ::$$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$ |
| − | Wird dagegen der Gleichanteil durch einen idealen Hochpass eliminiert, so ergeben sich die gleichsignalfreien Signale | + | Wird dagegen der Gleichanteil durch einen idealen Hochpass eliminiert, so ergeben sich die gleichsignalfreien Signale |
:$$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),\hspace{0.5cm}\varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$ | :$$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),\hspace{0.5cm}\varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$ | ||
| Zeile 24: | Zeile 24: | ||
| − | + | Hinweise: | |
| − | |||
| − | |||
*Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]]. | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]]. | ||
| − | *Bezug genommen wird insbesondere auf das Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]] | + | *Bezug genommen wird insbesondere auf das Kapitel [[Modulationsverfahren/Qualitätskriterien|Qualitätskriterien]] sowie auf das Kapitel [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen|Nichtlineare Verzerrungen]] im Buch „Lineare zeitinvarianteSysteme”. |
| − | |||
*Zur Lösung dieser Aufgabe sind folgende unbestimmte Integrale gegeben: | *Zur Lösung dieser Aufgabe sind folgende unbestimmte Integrale gegeben: | ||
:$$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ | :$$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$ | ||
| Zeile 73: | Zeile 70: | ||
'''(1)''' Aus der Grafik erkennt man $A_{\rm T} = 4\ \rm V$. Daraus ergibt sich mit $A_{\rm N} = 5\ \rm V$ der Modulationsgrad | '''(1)''' Aus der Grafik erkennt man $A_{\rm T} = 4\ \rm V$. Daraus ergibt sich mit $A_{\rm N} = 5\ \rm V$ der Modulationsgrad | ||
:$$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$ | :$$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$ | ||
| − | |||
| Zeile 86: | Zeile 82: | ||
'''(3)''' Der Klirrfaktor zweiter Ordnung ist $K_2 = 0.458/4.48 ≈ 0.102$. | '''(3)''' Der Klirrfaktor zweiter Ordnung ist $K_2 = 0.458/4.48 ≈ 0.102$. | ||
*Entsprechend gilt für den Klirrfaktor dritter Ordnung: $K_3 = 0.367/4.48 ≈ 0.082$. | *Entsprechend gilt für den Klirrfaktor dritter Ordnung: $K_3 = 0.367/4.48 ≈ 0.082$. | ||
| − | *Die weiteren Klirrfaktoren sind $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ sowie $K_6 ≈ 0.015$. | + | *Die weiteren Klirrfaktoren sind $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ sowie $K_6 ≈ 0.015$. |
*Damit erhält man für den Gesamtklirrfaktor: | *Damit erhält man für den Gesamtklirrfaktor: | ||
:$$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$ | :$$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$ | ||
| Zeile 95: | Zeile 91: | ||
[[Datei:P_ID1033__Mod_A_2_7_d.png|right|frame|Zur Berechnung der Verzerrungsleistung]] | [[Datei:P_ID1033__Mod_A_2_7_d.png|right|frame|Zur Berechnung der Verzerrungsleistung]] | ||
:$$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$ | ||
| − | *Hierbei ist berücksichtigt, dass das Fehlersignal $ε_{\rm A}(t)$ außerhalb des Intervalls von $t_1$ und $t_2$ gleich Null ist. | + | *Hierbei ist berücksichtigt, dass das Fehlersignal $ε_{\rm A}(t)$ außerhalb des Intervalls von $t_1$ und $t_2$ gleich Null ist. |
| − | *Wie aus der Skizze hervorgeht, ist $I_ε$ doppelt so groß als das Integral $I_γ$ der Hilfsgröße $γ$ im Intervall von Null bis $t_3 = (t_2 – t_1)/2 ≈ 0.1 \ \rm ms$: | + | *Wie aus der Skizze hervorgeht, ist $I_ε$ doppelt so groß als das Integral $I_γ$ der Hilfsgröße $γ$ im Intervall von Null bis $t_3 = (t_2 – t_1)/2 ≈ 0.1 \ \rm ms$: |
:$$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm mit}\hspace{0.5cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$ | :$$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm mit}\hspace{0.5cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$ | ||
*Eine Nebenrechnung liefert $I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)$ mit | *Eine Nebenrechnung liefert $I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)$ mit | ||
| Zeile 106: | Zeile 102: | ||
*Somit erhält man als Endergebnis: | *Somit erhält man als Endergebnis: | ||
:$$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$ | ||
| + | |||
| Zeile 114: | Zeile 111: | ||
P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} | P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} | ||
P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$ | P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$ | ||
| − | *Damit ergibt sich für | + | *Damit ergibt sich für die Leistung des Fehlersignals $ε_{\rm B}(t)$: |
:$$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$ | :$$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$ | ||
*Ein ähnliches Ergebnis hätte man auch nach folgendem Rechengang erhalten: | *Ein ähnliches Ergebnis hätte man auch nach folgendem Rechengang erhalten: | ||
:$$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$ | :$$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$ | ||
| − | *Der geringe Unterschied in beiden Rechengängen ist darauf zurückzuführen, dass die Fourierkoeffizienten $A_7$, $A_8$, ... zwar sehr klein sind, aber nicht Null. | + | *Der geringe Unterschied in beiden Rechengängen ist darauf zurückzuführen, dass die Fourierkoeffizienten $A_7$, $A_8$, ... zwar sehr klein sind, aber nicht Null. |
| + | |||
| Zeile 124: | Zeile 122: | ||
'''(6)''' Die Leistung des Quellensignals $q(t)$ beträgt $P_q = A_{\rm N}^2/2 = 12.5 V^2$. Daraus ergeben sich die beiden S/N–Verhältnisse: | '''(6)''' Die Leistung des Quellensignals $q(t)$ beträgt $P_q = A_{\rm N}^2/2 = 12.5 V^2$. Daraus ergeben sich die beiden S/N–Verhältnisse: | ||
:$$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$ | :$$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$ | ||
| − | *Dies zeigt, dass der Hüllkurvendemodular $\rm B$ (mit Hochpass) um etwa $6 \ \rm dB$ besser ist als der Demodulator $\rm A$ (mit Subtraktion). | + | *Dies zeigt, dass der Hüllkurvendemodular $\rm B$ (mit Hochpass) um etwa $6 \ \rm dB$ besser ist als der Demodulator $\rm A$ (mit Subtraktion). |
| − | + | *Anzumerken ist ferner, dass die Näherung $ρ_v = α_2 · P_q/K^2$ hier zum verfälschten Zahlenwert $ρ_v = 36.66$ führen würde. | |
| − | *Anzumerken ist ferner, dass die Näherung $ρ_v = α_2 · P_q/K^2$ hier zum verfälschten Zahlenwert $ρ_v = 36.66$ führen würde. | + | *Dieses unterschiedliche Ergebnis wird auf der Seite „Der Klirrfaktor” im Buch „Lineare zeitinvariante Systeme” ausführlich begründet, wobei genau die für die vorliegende Aufgabe getroffenen Voraussetzungen zugrunde gelegt sind. |
| − | *Dieses unterschiedliche Ergebnis wird auf der Seite „Der Klirrfaktor” im Buch „Lineare zeitinvariante Systeme” ausführlich begründet, wobei genau die für die vorliegende Aufgabe getroffenen Voraussetzungen zugrunde gelegt sind. | ||
Aktuelle Version vom 15. Februar 2022, 11:39 Uhr
Das cosinusförmige Quellensignal $q(t)$ mit Amplitude $A_{\rm N} = 5\ \rm V$ und Frequenz $f_{\rm N} = 1 \ \rm kHz$ wird $\rm ZSB$–amplitudenmoduliert. Für das Empfangssignal gilt bei dem vorausgesetzten idealen Kanal:
- $$r(t) = s(t) =\left(q(t) + A_{\rm T}\right) \cdot \cos (2\pi \cdot f_{\rm T}\cdot t )\hspace{0.05cm}.$$
Es handelt sich folglich um eine „ZSB–AM mit Träger”.
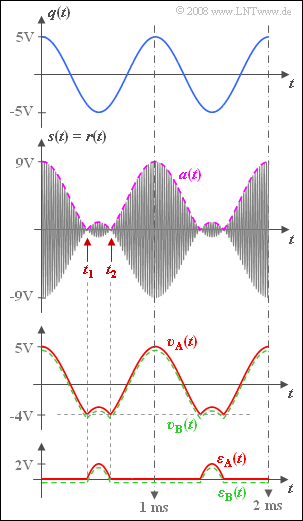
In der Grafik sind neben dem Quellensignal $q(t)$ und dem Empfangssignal $r(t)$ inklusive dessen Hüllkurve $a(t)$ auch das Sinkensignal $v(t)$ und das Fehlersignal
- $$ \varepsilon(t) = v(t) - q(t)$$
dargestellt. Das rot gezeichnete Sinkensignal
- $$v_{\rm A}(t) = a(t) - A_{\rm T}$$
gehört zu einem Hüllkurvendemodulator, bei dem von der Hüllkurve $a(t)$ genau der beim Sender zugeführte Träger $(A_{\rm T})$ subtrahiert wird.
Dieses Signal $v_{\rm A}(t)$ besitzt ebenso wie das zugehörige Fehlersignal $ε_{\rm A}(t)$ einen Gleichanteil. Aufgrund der Periodizität kann es durch die folgende Fourierreihe approximiert werden:
- $$v_{\rm A}(t) = A_0 + \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ), \hspace{0.3cm}{\rm mit}$$
- $$A_0 = 0.272\,{\rm V},\hspace{0.3cm}A_1 = 4.480\,{\rm V},\hspace{0.3cm}A_2 = 0.458\,{\rm V},\hspace{0.3cm}A_3 = -0.367\,{\rm V},\hspace{0.3cm}$$
- $$A_4 = 0.260\,{\rm V},\hspace{0.3cm}A_5 = -0.155\,{\rm V},\hspace{0.3cm}A_6 = 0.066\,{\rm V}\hspace{0.05cm}.$$
Wird dagegen der Gleichanteil durch einen idealen Hochpass eliminiert, so ergeben sich die gleichsignalfreien Signale
- $$ v_{\rm B}(t) = \sum_{n=1}^{6} A_i \cdot \cos (n \cdot \omega_{\rm N}\cdot t ),\hspace{0.5cm}\varepsilon_{\rm B}(t) = v_{\rm B}(t) - q(t) = a(t) - A_{\rm T} - A_0 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Hüllkurvendemodulation.
- Bezug genommen wird insbesondere auf das Kapitel Qualitätskriterien sowie auf das Kapitel Nichtlineare Verzerrungen im Buch „Lineare zeitinvarianteSysteme”.
- Zur Lösung dieser Aufgabe sind folgende unbestimmte Integrale gegeben:
- $$ \int { \cos (a x )}\hspace{0.1cm}{\rm d}x =\frac{1}{a} \cdot \sin (a x ), \hspace{0.5cm} \int { \cos^2 (a x )}\hspace{0.1cm}{\rm d}x = \frac{x}{2} +\frac{1}{4a} \cdot \sin (2a x ).$$
- Die Klirrfaktoren berechnen sich entsprechend den Gleichungen
- $$K_2 = {A_2}/{A_1}, \hspace{0.3cm} K_3 = {A_3}/{A_1}, \hspace{0.1cm} \text{...} \hspace{0.5cm} \Rightarrow \hspace{0.5cm}K = \sqrt{K_2^2 +K_3^2 + \text{...}}\hspace{0.1cm} .$$
Fragebogen
Musterlösung
- $$m = A_{\rm N}/A_{\rm T}\hspace{0.15cm}\underline { = 1.25}.$$
(2) Aus der Bedingung $a(t) = q(t) + A_{\rm T} = 0$ folgt direkt für die erste Nullstelle:
- $$ \cos (2\pi \cdot f_{\rm N}\cdot t_1 ) = \frac{-A_{\rm T}}{A_{\rm N}}= -0.8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1 = \frac{\rm arccos(-0.8)}{2\pi \cdot f_{\rm N}}\approx \frac{0.795 \cdot \pi}{2\pi \cdot f_{\rm N}} \hspace{0.05cm}.$$
- Mit $f_{\rm N} = 1 \ \rm kHz$ ergibt sich daraus $t_1\hspace{0.15cm}\underline { ≈ 0.4 \ \rm ms}$.
- Die zweite Nullstelle ist entsprechend $t_2\hspace{0.15cm}\underline { ≈ 0.6 \ \rm ms}$.
(3) Der Klirrfaktor zweiter Ordnung ist $K_2 = 0.458/4.48 ≈ 0.102$.
- Entsprechend gilt für den Klirrfaktor dritter Ordnung: $K_3 = 0.367/4.48 ≈ 0.082$.
- Die weiteren Klirrfaktoren sind $K_4 ≈ 0.058$, $K_5 ≈ 0.035$ sowie $K_6 ≈ 0.015$.
- Damit erhält man für den Gesamtklirrfaktor:
- $$ K = \sqrt{K_2^2 + K_3^2 + K_4^2 + K_5^2 + K_6^2 }\hspace{0.15cm}\underline { \approx 14.8 \%}.$$
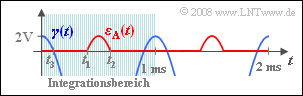
(4) Die Verzerrungsleistung ergibt sich aus Mittelung von $ε_{\rm A}(t)^2$ über eine Periodendauer $T_0 = 1\ \rm ms$:
- $$P_{\varepsilon \rm A} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{t_1}^{\hspace{0.1cm} t_2} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{I_{\varepsilon}}{T_{\rm 0}}\hspace{0.05cm}.$$
- Hierbei ist berücksichtigt, dass das Fehlersignal $ε_{\rm A}(t)$ außerhalb des Intervalls von $t_1$ und $t_2$ gleich Null ist.
- Wie aus der Skizze hervorgeht, ist $I_ε$ doppelt so groß als das Integral $I_γ$ der Hilfsgröße $γ$ im Intervall von Null bis $t_3 = (t_2 – t_1)/2 ≈ 0.1 \ \rm ms$:
- $$I_{\gamma} = \int_{0}^{\hspace{0.1cm} t_3} {\gamma^2(t) }\hspace{0.1cm}{\rm d}t \hspace{0.5cm}{\rm mit}\hspace{0.5cm} \gamma(t) = 2 \cdot \left( A_{\rm N} \cdot \cos (\omega_{\rm N}\cdot t ) - A_{\rm T}\right)\hspace{0.05cm}.$$
- Eine Nebenrechnung liefert $I_{\gamma} = 4 \cdot \left( I_1 + I_2 + I_3 \right)$ mit
- $$I_1 = A_{\rm N}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {\cos^2 (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = A_{\rm N}^2 \cdot \left[ \frac{t_3}{2} + \frac{\sin (2 \omega_{\rm N}\cdot t_3 )}{4 \omega_{\rm N}} \right] = 25\,{\rm V}^2 \cdot \left[ 0.05\,{\rm ms} + 0.0378\,{\rm ms} \right] = 2.196 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$
- $$ I_2 = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \int_{0}^{\hspace{0.1cm} t_3} \hspace{-0.2cm}{\cos (\omega_{\rm N}\cdot t ) }\hspace{0.1cm}{\rm d}t = - 2 \cdot A_{\rm N}\cdot A_{\rm T} \cdot \frac{\sin (\omega_{\rm N}\cdot t_3 )}{\omega_{\rm N}} = - 2 \cdot 5\,{\rm V} \cdot 4\,{\rm V}\cdot 0.0935\,{\rm ms} = -3.742 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm},$$
- $$ I_3 = A_{\rm T}^2 \cdot \int_{0}^{\hspace{0.1cm} t_3} {}\hspace{0.1cm}{\rm d}t = A_{\rm T}^2 \cdot {t_3} = 1.6 \cdot 10^{-3}\,{\rm V^2 s}$$
- $$\Rightarrow \hspace{0.3cm}I_{\gamma} = 0.216 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}I_{\varepsilon} = 2 \cdot I_{\gamma} =0.432 \cdot 10^{-3}\,{\rm V^2 s} \hspace{0.05cm}.$$
- Somit erhält man als Endergebnis:
- $$P_{\varepsilon \rm A} = {I_{\varepsilon}}/{T_{\rm 0}}\hspace{0.15cm}\underline {=0.432 \,{\rm V^2 }}\hspace{0.05cm}.$$
(5) Die beiden Sinkensignale $v_{\rm A}(t)$ und $v_{\rm B}(t)$ unterscheiden sich ebenso wie die beiden Fehlersignale $ε_{\rm A}(t)$ und $ε_{\rm B}(t)$ um den Gleichanteil $A_0$. Deshalb gilt:
- $$ P_{\varepsilon \rm B} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm B}^2(t) }\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\left[\varepsilon_{\rm A}(t) - A_0 \right]^2}\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Hierfür kann auch geschrieben werden:
- $$P_{1} = \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}^2(t) }\hspace{0.1cm}{\rm d}t = P_{\varepsilon \rm A} \hspace{0.05cm},\hspace{0.3cm} P_{2} = - 2 A_0 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} {\varepsilon_{\rm A}(t) }\hspace{0.1cm}{\rm d}t = - 2 A_0^2 \hspace{0.05cm},\hspace{0.3cm} P_{3} = A_0^2 \cdot \frac{1}{T_{\rm 0}}\hspace{0.05cm} \cdot \int_{0}^{T_0} { }\hspace{0.1cm}{\rm d}t = A_0^2 \hspace{0.05cm}.$$
- Damit ergibt sich für die Leistung des Fehlersignals $ε_{\rm B}(t)$:
- $$P_{\varepsilon \rm B} = P_{\varepsilon \rm A}- A_0^2 = 0.432\,{\rm V}^2 - (0.272\,{\rm V})^2 \hspace{0.15cm}\underline {= 0.358\,{\rm V}^2} \hspace{0.05cm}.$$
- Ein ähnliches Ergebnis hätte man auch nach folgendem Rechengang erhalten:
- $$ P_{\varepsilon \rm B} = \frac{1\,{\rm V}^2}{2} \cdot \left[ (5 - 4.48)^2 + 0.458^2 + 0.367^2 + ... + 0.066^2 \right] \approx 0.356\,{\rm V}^2 \hspace{0.05cm}.$$
- Der geringe Unterschied in beiden Rechengängen ist darauf zurückzuführen, dass die Fourierkoeffizienten $A_7$, $A_8$, ... zwar sehr klein sind, aber nicht Null.
(6) Die Leistung des Quellensignals $q(t)$ beträgt $P_q = A_{\rm N}^2/2 = 12.5 V^2$. Daraus ergeben sich die beiden S/N–Verhältnisse:
- $$\rho_{v {\rm A}} = \frac{P_{q}}{P_{\varepsilon \rm A}} \hspace{0.15cm}\underline {= 28.94} \hspace{0.05cm}, \hspace{0.3cm} \rho_{v {\rm B}} = \frac{P_{q}}{P_{\varepsilon \rm B}}\hspace{0.15cm}\underline { = 34.92} \hspace{0.05cm}.$$
- Dies zeigt, dass der Hüllkurvendemodular $\rm B$ (mit Hochpass) um etwa $6 \ \rm dB$ besser ist als der Demodulator $\rm A$ (mit Subtraktion).
- Anzumerken ist ferner, dass die Näherung $ρ_v = α_2 · P_q/K^2$ hier zum verfälschten Zahlenwert $ρ_v = 36.66$ führen würde.
- Dieses unterschiedliche Ergebnis wird auf der Seite „Der Klirrfaktor” im Buch „Lineare zeitinvariante Systeme” ausführlich begründet, wobei genau die für die vorliegende Aufgabe getroffenen Voraussetzungen zugrunde gelegt sind.