Aufgaben:Aufgabe 1.1: Musiksignale: Unterschied zwischen den Versionen
Aus LNTwww
| Zeile 62: | Zeile 62: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | '''(1)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | ||
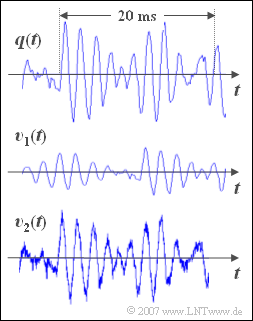
| − | *Im markierten Bereich von $20$ Millisekunden sind ca. $10$ Schwingungen zu erkennen. | + | *Im markierten Bereich von $20$ Millisekunden sind ca. $10$ Schwingungen zu erkennen. |
*Daraus folgt für die Signalfrequenz näherungsweise das Ergebnis $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$. | *Daraus folgt für die Signalfrequenz näherungsweise das Ergebnis $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$. | ||
| Zeile 68: | Zeile 68: | ||
'''(2)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | '''(2)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | ||
| − | *Das Signal <math>v_1(t)</math> ist gegenüber dem Orginalsignal <math>q(t)</math> unverzerrt. Es gilt: $v_1(t)=\alpha \cdot q(t-\tau) .$ | + | *Das Signal <math>v_1(t)</math> ist gegenüber dem Orginalsignal <math>q(t)</math> unverzerrt. Es gilt: $v_1(t)=\alpha \cdot q(t-\tau) .$ |
*Eine Dämpfung <math>\alpha</math> und eine Laufzeit <math>\tau</math> führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original. | *Eine Dämpfung <math>\alpha</math> und eine Laufzeit <math>\tau</math> führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original. | ||
| Zeile 76: | Zeile 76: | ||
'''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
*Man erkennt sowohl im dargestellten Signalverlauf <math>v_2(t)</math> als auch im Audiosignal ''additives Rauschen'' ⇒ <u>Lösungsvorschlag 3</u>. | *Man erkennt sowohl im dargestellten Signalverlauf <math>v_2(t)</math> als auch im Audiosignal ''additives Rauschen'' ⇒ <u>Lösungsvorschlag 3</u>. | ||
| − | *Der Signalrauschabstand beträgt dabei ca. $\text{30 dB}$; dies ist aber aus dieser Darstellung nicht erkennbar. | + | *Der Signalrauschabstand beträgt dabei ca. $\text{30 dB}$; dies ist aber aus dieser Darstellung nicht erkennbar. |
*Richtig ist aber auch der <u>Lösungsvorschlag 1</u>: Ohne diesen Rauschanteil wäre <math>v_2(t)</math> identisch mit <math>q(t)</math>. | *Richtig ist aber auch der <u>Lösungsvorschlag 1</u>: Ohne diesen Rauschanteil wäre <math>v_2(t)</math> identisch mit <math>q(t)</math>. | ||
| − | '''(4)''' Das Signal <math>v_1(t)</math> ist formgleich mit dem Originalsignal <math>q(t)</math> und unterscheidet sich von diesem lediglich | + | '''(4)''' Das Signal <math>v_1(t)</math> ist formgleich mit dem Originalsignal <math>q(t)</math> und unterscheidet sich von diesem lediglich durch |
| − | * | + | *den Amplitudenfaktor $\alpha = \underline{\text{0.3}}$ (dies entspricht etwa $\text{–10 dB)}$ |
*und die Laufzeit $\tau = \underline{10\,\text{ms}}$. | *und die Laufzeit $\tau = \underline{10\,\text{ms}}$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 8. April 2021, 09:15 Uhr
Nebenstehend sehen Sie einen ca. $\text{30 ms}$ langen Ausschnitt eines Musiksignals \(q(t)\). Es handelt sich um das Stück „Für Elise” von Ludwig van Beethoven.
- Darunter gezeichnet sind zwei Sinkensignale \(v_1(t)\) und \(v_2(t)\), die nach der Übertragung des Musiksignals \(q(t)\) über zwei unterschiedliche Kanäle aufgezeichnet wurden.
- Mit Hilfe der nachfolgenden Bedienelemente können Sie sich die jeweils ersten vierzehn Sekunden der drei Audiosignale \(q(t)\), \(v_1(t)\) und \(v_2(t)\) anhören.
Originalsignal \(q(t)\)
Sinkensignal \(v_1(t)\)
Sinkensignal \(v_2(t)\)
Hinweis:
- Die Aufgabe gehört zum Kapitel Prinzip der Nachrichtenübertragung.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 2:
- Im markierten Bereich von $20$ Millisekunden sind ca. $10$ Schwingungen zu erkennen.
- Daraus folgt für die Signalfrequenz näherungsweise das Ergebnis $f = {10}/(20 \,\text{ms}) = 500 \,\text{Hz}$.
(2) Richtig ist der Lösungsvorschlag 1:
- Das Signal \(v_1(t)\) ist gegenüber dem Orginalsignal \(q(t)\) unverzerrt. Es gilt: $v_1(t)=\alpha \cdot q(t-\tau) .$
- Eine Dämpfung \(\alpha\) und eine Laufzeit \(\tau\) führen nicht zu Verzerrungen, sondern das Signal ist dann nur leiser und es kommt später als das Original.
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Man erkennt sowohl im dargestellten Signalverlauf \(v_2(t)\) als auch im Audiosignal additives Rauschen ⇒ Lösungsvorschlag 3.
- Der Signalrauschabstand beträgt dabei ca. $\text{30 dB}$; dies ist aber aus dieser Darstellung nicht erkennbar.
- Richtig ist aber auch der Lösungsvorschlag 1: Ohne diesen Rauschanteil wäre \(v_2(t)\) identisch mit \(q(t)\).
(4) Das Signal \(v_1(t)\) ist formgleich mit dem Originalsignal \(q(t)\) und unterscheidet sich von diesem lediglich durch
- den Amplitudenfaktor $\alpha = \underline{\text{0.3}}$ (dies entspricht etwa $\text{–10 dB)}$
- und die Laufzeit $\tau = \underline{10\,\text{ms}}$.