Aufgaben:Aufgabe 2.4Z: Dreiecksignal

• Zurück zum Buch

Vorgegebenes Dreiecksignal

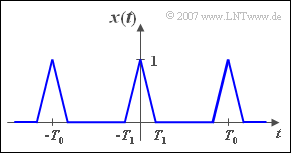
Wir betrachten das mit  $T_0$  periodische Signal  ${x(t)}$  entsprechend nebenstehender Skizze, wobei für den zweiten Signalparameter  $T_1 ≤ T_0/2$  gelten soll.  Dieses Signal ist dimensionslos und auf  $1$  begrenzt.

In der Teilaufgabe  (3)  wird die auf nur  $N = 3$  Koeffizienten basierende Fourierreihendarstellung  $x_3(t)$  verwendet.

Die Differenz zwischen der abgebrochenen Fourierreihe und dem tatsächlichen Signal lautet:

$$\varepsilon_3(t)=x_3(t)-x(t).$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Fourierreihe.
• Eine kompakte Zusammenfassung der Thematik finden Sie in den beiden Lernvideos

Zur Berechnung der Fourierkoeffizienten

Eigenschaften der Fourierreihendarstellung

• Zur Lösung der Aufgabe können Sie das folgende bestimmte Integral benutzen  $(n$ sei ganzzahlig$)$:

$$\int u \cdot \cos(au)\,{\rm d}u = \frac{\cos(au)}{a^2} + \frac{u \cdot \sin(au)}{a}.$$

Fragebogen

1

Welche der folgenden Aussagen treffen für alle zulässigen  $T_0$  und  $T_1$  zu?

	Der Gleichanteil beträgt  $A_0 = T_1/T_0$.
	Alle Sinuskoeffizienten  $B_n$  sind Null.
	Alle Cosinuskoeffizienten  $A_n$  mit geradzahligem  $n$  sind Null.

2

Berechnen Sie die Fourierkoeffizienten  $A_n$  in allgemeiner Form.  Welche Werte ergeben sich für  $A_1$,  $A_2$  und  $A_3$  mit  $T_1/T_0 = 0.25$?

$A_1\ = \ $

$A_2\ = \ $

$A_3\ = \ $

3

Schreiben Sie die Funktion  ${x(t)}$  als Fourierreihe und brechen Sie diese nach  $N = 3$  Koeffizienten ab.  Wie groß ist der Fehler  $\varepsilon_3(t = 0)$?

$\varepsilon_3(t = 0)\ = \ $

Musterlösung

Musterlösung

(1)  Richtig sind die Lösungsvorschläge 1 und 2:

• Der Gleichanteil ist tatsächlich  $T_1/T_0$.  Da  ${x(t)}$  eine gerade Funktion ist, sind alle Sinuskoeffizienten  $B_n = 0$.
• Die geradzahligen Cosinuskoeffizienten  $A_{2n}$  verschwinden nur dann, wenn  $T_1 = T_0/2$  ist.
• In diesem Fall ist die Bedingung  ${x(t)} = 2A_0 - x(t - T_0/2)$  erfüllt  $($mit $A_0 = 0.5)$.

(2)  Unter Ausnutzung der Symmetrieeigenschaft  ${x(-t)} = {x(t)}$  erhält man:

$$A_n=2 \cdot \frac{2}{T_0}\cdot \hspace{-0.1cm}\int_0^{T_1}(1-\frac{t}{T_1})\cos(2\pi n\frac{t}{T_0})\, {\rm d}t.$$

• Dies führt zu zwei Teilintegralen  $I_1$  und  $I_2$.  Das erste lautet:

$$I_1=\frac{4}{T_0} \cdot \hspace{-0.1cm} \int_0^{T_1}\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{2}{\pi n}\sin(2\pi n\frac{T_1}{T_0}).$$

• Für das zweite Integral gilt mit dem Integral auf der Angabenseite:

$$I_2=\frac{-4}{T_0\cdot T_1}\cdot \hspace{-0.1cm}\int_0^{T_1}t\cdot\cos(2\pi n\frac{t}{T_0})\,{\rm d}t=\frac{-4}{T_0\cdot T_1}\cdot \hspace{0.1cm}\left[\frac{T^2_0 \cdot \cos(2\pi nt/T_0)}{4\pi^2n^2}+\frac{T_0 \cdot t \cdot \sin(2\pi nt/T_0)}{2\pi n}\right]^{T_1}_0.$$

• Dieses letzte Integral kann wie folgt zusammengefasst werden:

$$I_2=\frac{-\cos(2\pi nT_1/T_0)}{\pi^2 n^2T_1/T_0}+\frac{1}{\pi^2 n^2 T_1/T_0}-I_1.$$

• Daraus folgt mit  $1 - \cos(2\alpha) = 2 \cdot \sin^2(\alpha)$:

$$A_n=I_1+I_2=\frac{1-\cos(2\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}=\frac{2\sin^2 (\pi nT_1/T_0)}{\pi^2 n^2 T_1/T_0}.$$

• Für  $T_1/T_0 = 0.25$  erhält man:

$$A_n=\frac{8\sin^2 (\pi n/4)}{\pi^2 n^2}.$$

• Insbesondere gilt:

$$A_1=\frac{8}{\pi^2}\sin^2(\pi/4)=\frac{4}{\pi^2}\hspace{0.15cm}\underline{\approx 0.405},\hspace{0.5cm} A_2=\frac{2}{\pi^2}\sin^2(\pi/2)=\frac{2}{\pi^2}\hspace{0.15cm}\underline{\approx 0.202},\hspace{0.5cm} A_3=\frac{8}{9\pi^2}\sin^2(3\pi/4)=\frac{4}{9\pi^2}\hspace{0.15cm}\underline{\approx 0.045}.$$

(3)  Es gilt:

$$x_3(t)=\frac{1}{4}+\frac{4}{\pi^2}\left[\cos(\omega_0 t)+\frac{1}{2}\cos(2\omega_0 t)+\frac{1}{9}\cos(3\omega_0 t)\right].$$

• Zum Zeitpunkt  $t = 0$  ergibt sich hieraus:

$$x_3(t=0)=\frac{1}{4}+\frac{4}{\pi^2}\cdot \frac{29}{18}\approx 0.9 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\varepsilon_3(t=0)=x_3(t=0)-x(t=0)\hspace{0.15cm}\underline{=-0.1}.$$

• Für die Zeit  $t = 0$  und bei Vielfachen der Periodendauer  $T_0$  (jeweils Spitze der Dreiecksfunktionen)  ist die Abweichung betragsmäßig am größten.