Aufgaben:Aufgabe 2.9: Symmetrische Verzerrungen

• Zurück zum Buch

Sende– und Empfangsspektrum im äquivalenten Tiefpass-Bereich

Das aus zwei Anteilen zusammengesetzte Quellensignal

$$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$

wird amplitudenmoduliert und über einen linear verzerrenden Übertragungskanal übertragen. 

• Die Trägerfrequenz ist  $f_{\rm T}$  und der zugesetzte Gleichanteil  $A_{\rm T}$. 
• Es liegt also eine  "Zweiseitenband-Amplitudenmoduluation  $\rm (ZSB–AM)$  mit Träger"  vor.

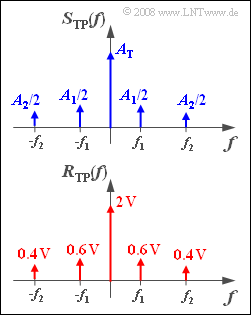
Die obere Grafik zeigt das Spektrum  $S_{\rm TP}(f)$  des äquivalenten Tiefpass–Signals in schematischer Form.  Das bedeutet,  dass die Längen der gezeichneten Diraclinien nicht den tatsächlichen Werten von  $A_{\rm T}$,  $A_1/2$  und  $A_2/2$  entsprechen.

Messtechnisch erfasst wurde die Spektralfunktion  $R(f)$  des Empfangssignals.  In der unteren Grafik sehen Sie das daraus berechnete äquivalente Tiefpass–Spektrum  $R_{\rm TP}(f)$.

Der Kanalfrequenzgang ist durch einige Stützwerte ausreichend genau beschrieben:

$$ H_{\rm K}(f = f_{\rm T}) = 0.5,$$

$$H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,$$

$$ H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Hüllkurvendemodulation.
• Bezug genommen wird insbesondere auf das Kapitel  Beschreibung mit Hilfe des äquivalenten Tiefpass-Signals.

Fragebogen

1

Ermitteln Sie die Amplituden von Träger– und Quellensignal.

$A_{\rm T} \ = \hspace{0.17cm} $ $\ \rm V$

$A_1 \ = \ $ $\ \rm V$

$A_2 \ = \ $ $\ \rm V$

2

Zu welcher Art von Verzerrung hätte der Einsatz eines Hüllkurvendemodulators bei idealem Kanal   ⇒   $H_{\rm K}(f) = 1$  geführt?

	Keine Verzerrungen.
	Lineare Verzerrungen.
	Nichtlineare Verzerrungen.

3

Berechnen Sie das äquivalente Tiefpass–Signal und beantworten Sie folgende Fragen.  Ist es zutreffend,  dass

	$r_{\rm TP}(t)$  stets reell ist,
	$r_{\rm TP}(t)$  stets größer oder gleich Null ist,
	die Phasenfunktion  $ϕ(t)$  die Werte  $0^\circ$  und  $180^\circ$  annehmen kann?

4

Zu welchen Verzerrungen führt der Hüllkurvendemodulator beim betrachteten Übertragungskanal?

	Keine Verzerrungen.
	Lineare Verzerrungen.
	Nichtlineare Verzerrungen.

Musterlösung

Musterlösung

(1)  Anhand der Grafiken auf der Angabenseite sind folgende Aussagen möglich:

$${A_{\rm T}} \cdot 0.5 = 2 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm T} \hspace{0.15cm}\underline {= 4 \,{\rm V}},$$

$${A_{\rm 1}}/{2} \cdot 0.4 = 0.6\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 1} \hspace{0.15cm}\underline {= 3 \,{\rm V}},$$

$${A_{\rm 2}}/{2} \cdot 0.2 = 0.4\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 2} \hspace{0.15cm}\underline {= 4 \,{\rm V}}\hspace{0.05cm}.$$

(2)  Richtig ist der  Lösungsvorschlag 3:

• Der Modulationsgrad ergibt sich zu  $m = (A_1 + A_2)/A_T = 1.75$.
• Damit ergeben sich bei Verwendung eines Hüllkurvendemodulators starke nichtlineare Verzerrungen.
• Ein Klirrfaktor kann aber nicht angegeben werden,  da das Quellensignal zwei Frequenzanteile beinhaltet.

(3)  Richtig sind  die Aussagen 1 und 2:

• Die Fourierrücktransformation von  $R_{\rm TP}(f)$  führt zum Ergebnis:

$$ r_{\rm TP}(t) = 2 \,{\rm V} + 1.2 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.8 \,{\rm V} \cdot \cos(2 \pi f_2 t )\hspace{0.05cm}.$$

• Diese Funktion ist stets reell und nicht–negativ.
• Damit gilt gleichzeitig  $ϕ(t) = 0$.  Dagegen ist  $ϕ(t) = 180^\circ$  nicht möglich.

(4)  Ein Vergleich der beiden Signale

$$q(t) = 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 4 \,{\rm V} \cdot \cos(2 \pi f_2 t ),$$

$$ v(t) = 0.4 \cdot 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.2 \cdot 4 \,{\rm V} \cdot \cos(2 \pi f_2 t )$$

zeigt, dass nun lineare Verzerrungen – genauer gesagt:  Dämpfungsverzerrungen – auftreten   ⇒   Lösungsvorschlag 2.

• Der Kanal  $H_{\rm K}(f)$  hat hier den positiven Effekt,  dass anstelle von irreversiblen nichtlinearen Verzerrungen nun lineare Verzerrungen entstehen,  die durch ein nachgeschaltetes Filter eliminiert werden können.
• Dies ist darauf zurückzuführen,  dass durch die stärkere Dämpfung des Quellensignals  $q(t)$  im Vergleich zum Trägersignal  $z(t)$  der Modulationsgrad herabgesetzt wird von  $m = 1.75$  auf 

$$m = (0.4 · 3 \ \rm V + 0.2 · 4 \ \rm V)/(0.5 · 4 \ \rm V) = 1.$$