Aufgaben:Aufgabe 4.5: Ortskurve bei ZSB-AM: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} 250px|right|* ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch +…“) |
|||
| (19 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signaldarstellung/Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion |
}} | }} | ||
| − | [[Datei: | + | [[Datei:P_ID751__Sig_A_4_5_neu.png|250px|right|frame|Spektrum des analytischen Signals]] |
| + | Wir betrachten ein ähnliches Übertragungsszenario wie in der [[Aufgaben:Aufgabe_4.4:_Zeigerdiagramm_bei_ZSB-AM|Aufgabe 4.4]] (aber nicht das gleiche): | ||
| + | * ein sinusförmiges Nachrichtensignal mit der Amplitude $A_{\rm N} = 2 \ \text{V}$ und der Frequenz $f_{\rm N} = 10 \ \text{kHz}$, | ||
| + | *ZSB-Amplitudenmodulation ohne Trägerunterdrückung mit der Trägerfrequenz $f_{\rm T} = 50 \ \text{kHz}$. | ||
| + | |||
| + | Nebenstehend sehen Sie die Spektralfunktion $S_+(f)$ des analytischen Signals $s_+(t)$. | ||
| + | |||
| + | Berücksichtigen Sie bei der Lösung, dass das äquivalente Tiefpass-Signal auch in der Form | ||
| + | |||
| + | :$$s_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)} $$ | ||
| + | |||
| + | dargestellt werden kann, wobei $a(t) ≥ 0$ gelten soll. Für $\phi(t)$ ist der Wertebereich $–\pi < \phi(t) \leq +\pi$ zulässig und es gilt die allgemeingültige Gleichung: | ||
| + | |||
| + | :$$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\big[s_{\rm | ||
| + | TP}(t)\big]}{{\rm Re}\big[s_{\rm TP}(t)\big]}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Äquivalentes_Tiefpass-Signal_und_zugehörige_Spektralfunktion|Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion]]. | ||
| + | |||
| + | *Sie können Ihre Lösung mit dem interaktiven Applet [[Applets:Physikalisches_Signal_%26_Äquivalentes_TP-Signal|Physikalisches Signal & Äquivalentes Tiefpass-Signal]] ⇒ „Ortskurve” überprüfen. | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie das äquivalente Tiefpass-Signal $s_{\rm TP}(t)$ im Frequenz– und Zeitbereich. Welchen Wert besitzt $s_{\rm TP}(t)$ zum Startzeitpunkt $t = 0$? |
| − | |type="[] | + | |type="{}"} |
| − | + | $\text{Re}[s_{\text{TP}}(t=0)]\ = \ $ { 1 3% } $\text{V}$ | |
| − | + | $\text{Im}[s_{\text{TP}}(t=0 )]\ = \ $ { 0. } $\text{V}$ | |
| + | {Welche Werte weist $s_{\rm TP}(t)$ zu den Zeitpunkten $t = 10 \ {\rm µ} \text{s}= T_0/10$, $t = 25 \ {\rm µ} \text{s}= T_0/4$, $t = 75 \ {\rm µ} \text{s}= 3T_0/4$ und $T_0 = 100 \ {\rm µ}s$ auf? <br>Zeigen Sie, dass alle Werte rein reell sind. | ||
| + | |type="{}"} | ||
| + | $\text{Re}[s_{\text{TP}}(t=10 \ {\rm µ} \text{s})]\ = \ $ { 2.176 3% } $\text{V}$ | ||
| + | $\text{Re}[s_{\text{TP}}(t=25 \ {\rm µ} \text{s})] \ = \ $ { 3 3% } $\text{V}$ | ||
| + | $\text{Re}[s_{\text{TP}}(t=75 \ {\rm µ} \text{s})]\ = \ $ { -1.03--0.97 } $\text{V}$ | ||
| + | $\text{Re}[s_{\text{TP}}(t=100 \ {\rm µ} \text{s})]\ = \ $ { 1 3% } $\text{V}$ | ||
| − | { | + | {Wie lautet die Betragsfunktion $a(t)$ im Zeitbereich? Welche Werte ergeben sich zu den Zeiten $t = 25 \ {\rm µ} \text{s}$ und $t = 75 \ {\rm µ} \text{s}$? |
|type="{}"} | |type="{}"} | ||
| − | + | $a(t=25 \ {\rm µ} \text{s})\ = \ $ { 3 3% } $\text{V}$ | |
| + | $a(t=75 \ {\rm µ} \text{s})\ = \ $ { 1 3% } $\text{V}$ | ||
| + | {Geben Sie die Phasenfunktion $\phi(t)$ im Zeitbereich allgemein an. Welche Werte ergeben sich zu den Zeiten $t = 25 \ {\rm µ} \text{s}$ und $t = 75 \ {\rm µ} \text{s}$? | ||
| + | |type="{}"} | ||
| + | $\phi(t=25 \ {\rm µ} \text{s}) \ = \ $ { 0. } $\text{Grad}$ | ||
| + | $\phi(t=75\ {\rm µ} \text{s})\ = \ $ { 180 1% } $\text{Grad}$ | ||
| Zeile 24: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
| + | |||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | |
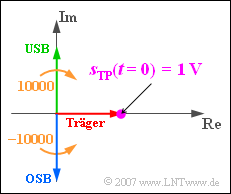
| + | [[Datei:P_ID755__Sig_A_4_5_a_neu.png|250px|right|frame|Ortskurve zur Zeit $t = 0$]] | ||
| + | '''(1)''' Verschiebt man alle Diraclinien jeweils um $f_{\rm T} = 50 \ \text{kHz}$ nach links, so liegen diese bei $-\hspace{-0.08cm}10 \ \text{kHz}$, $0$ und $+10 \ \text{kHz}$. | ||
| + | *Die Gleichung für $s_{\rm TP}(t)$ lautet mit $\omega_{10} = 2 \pi \cdot 10 \ \text{kHz}$: | ||
| + | |||
| + | :$$s_{\rm TP}(t) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 | ||
| + | \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} | ||
| + | \omega_{\rm 10} \hspace{0.05cm} t }+{\rm j}\cdot {\rm 1 | ||
| + | \hspace{0.05cm} V} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} | ||
| + | \omega_{\rm 10} \hspace{0.05cm} t }$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm} s_{\rm TP}(t = 0) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 | ||
| + | \hspace{0.05cm} V} +{\rm j}\cdot {\rm 1 \hspace{0.05cm} V}= {\rm 1 | ||
| + | \hspace{0.05cm} V}.$$ | ||
| + | |||
| + | :$$\Rightarrow \hspace{0.3cm} {\rm Re}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= {+\rm 1 \hspace{0.05cm} V}}, \hspace{0.2cm}{\rm Im}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= 0} | ||
| + | .$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Obige Gleichung kann man nach dem [[Signaldarstellung/Zum_Rechnen_mit_komplexen_Zahlen#Darstellung_nach_Betrag_und_Phase|Satz von Euler]] mit $T_0 = 1/f_{\rm N} = 100 \ {\rm µ} \text{s}$ wie folgt umformen: | ||
| + | |||
| + | :$$\frac{s_{\rm TP}(t)}{{\rm 1 \hspace{0.05cm} V}}\hspace{-0.05cm} =\hspace{-0.05cm}1\hspace{-0.05cm} - \hspace{-0.05cm}{\rm | ||
| + | j}\cdot \cos({ \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm} \sin({ | ||
| + | \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm}{\rm j}\cdot \cos({ | ||
| + | \omega_{\rm 10}\hspace{0.05cm} t })\hspace{-0.05cm} + \hspace{-0.05cm} \sin({ \omega_{\rm | ||
| + | 10}\hspace{0.05cm} t }) = 1+2 \cdot \sin(2 \pi | ||
| + | {t}/{T_0}) .$$ | ||
| + | |||
| + | *Damit ist gezeigt, dass $s_{\rm TP}(t)$ für alle Zeiten $t$ reell ist. | ||
| + | *Für die gesuchten Zahlenwerte erhält man: | ||
| + | |||
| + | :$$s_{\rm TP}(t = {\rm 10 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 | ||
| + | \hspace{0.05cm} V} \cdot \left[1+2 \cdot | ||
| + | \sin(36^\circ)\right]\hspace{0.15 cm}\underline{={{\rm +2.176 \hspace{0.05cm} V}}},$$ | ||
| + | |||
| + | :$$s_{\rm TP}(t = {\rm 25 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 | ||
| + | \hspace{0.05cm} V} \cdot \left[1+2 \cdot | ||
| + | \sin(90^\circ)\right]\hspace{0.15 cm}\underline{={{\rm +3 \hspace{0.05cm} V}}},$$ | ||
| + | |||
| + | :$$s_{\rm TP}(t = {\rm 75 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 | ||
| + | \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(270^\circ)\right]\hspace{0.15 cm}\underline{= | ||
| + | -{{\rm 1 \hspace{0.05cm} V}}},$$ | ||
| + | |||
| + | :$$s_{\rm TP}(t = {\rm 100 \hspace{0.1cm}{\rm µ} s}) = s_{\rm TP}(t = | ||
| + | 0) \hspace{0.15 cm}\underline{={{\rm +1 \hspace{0.05cm} V}}}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Definitionsgemäß gilt $a(t) = |s_{\rm TP}(t)|$. Damit erhält man folgende Zahlenwerte: | ||
| + | |||
| + | :$$a(t = {\rm 25 \hspace{0.1cm} {\rm µ} s}) = s_{\rm TP}(t = {\rm 25 | ||
| + | \hspace{0.05cm}{\rm µ} s}) \hspace{0.15 cm}\underline{= {\rm +3 \hspace{0.05cm} V}} , | ||
| + | \hspace{4.15 cm}$$ | ||
| + | |||
| + | :$$a(t = {\rm 75 \hspace{0.1cm} {\rm µ} s}) = |s_{\rm TP}(t = {\rm 75 | ||
| + | \hspace{0.05cm} {\rm µ} s})| \hspace{0.15 cm}\underline{= {\rm +1 \hspace{0.05cm} V}} .$$ | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Allgemein gilt für die Phasenfunktion: | ||
| + | |||
| + | :$$\phi(t)= {\rm arc} \left[s_{\rm TP}(t)\right]= {\rm arctan} | ||
| + | \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm | ||
| + | Re}\left[s_{\rm TP}(t)\right]}$$ | ||
| + | |||
| + | Aufgrund der Tatsache, dass hier für alle Zeiten ${\rm Im}[s_{\rm TP}(t)] = 0$ ist, erhält man hieraus das Ergebnis: | ||
| + | * Falls ${\rm Re}[s_{\rm TP}(t)] > 0$ gilt, ist die Phase $\phi(t) = 0$. | ||
| + | * Dagegen gilt bei negativem Realteil: $\phi(t) = \pi$. | ||
| + | |||
| + | |||
| + | Wir beschränken uns hier auf den Zeitbereich einer Periode: $0 \leq t \leq T_0$. | ||
| + | *Im Bereich zwischen $t_1$ und $t_2$ liegt eine Phase von $180^\circ$ vor, ansonsten gilt $\text{Re}[s_{\rm TP}(t)] \geq 0$. | ||
| + | |||
| + | *Zur Berechung von $t_1$ kann das Ergebnis der Teilaufgabe '''(2)''' herangezogen werden: | ||
| + | |||
| + | :$$\sin(2 \pi \cdot {t_1}/{T_0}) = -0.5 \hspace{0.3cm} \Rightarrow | ||
| + | \hspace{0.3cm} 2 \pi \cdot {t_1}/{T_0} = 2 \pi \cdot | ||
| + | {7}/{12}\hspace{0.3cm}{\rm (entspricht}\hspace{0.2cm}210^\circ | ||
| + | )$$ | ||
| + | |||
| + | *Daraus erhält man $t_1 = 7/12 · T_0 = 58.33 \ {\rm µ} \text{s}$. | ||
| + | *Durch ähnliche Überlegungen kommt man zum Ergebnis: $t_2 = 11/12 · T_0 = 91.63 \ {\rm µ} \text{s}$. | ||
| + | |||
| + | |||
| + | Die gesuchten Werte sind somit: | ||
| + | :$$\phi(t = 25 \ {\rm µ} \text{s}) \; \underline { = 0},$$ | ||
| + | :$$\phi(t = 75 \ {\rm µ} \text{s}) \; \underline { = 180^{\circ}}\; (= \pi).$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | ||
Aktuelle Version vom 11. Mai 2021, 13:44 Uhr
Wir betrachten ein ähnliches Übertragungsszenario wie in der Aufgabe 4.4 (aber nicht das gleiche):
- ein sinusförmiges Nachrichtensignal mit der Amplitude $A_{\rm N} = 2 \ \text{V}$ und der Frequenz $f_{\rm N} = 10 \ \text{kHz}$,
- ZSB-Amplitudenmodulation ohne Trägerunterdrückung mit der Trägerfrequenz $f_{\rm T} = 50 \ \text{kHz}$.
Nebenstehend sehen Sie die Spektralfunktion $S_+(f)$ des analytischen Signals $s_+(t)$.
Berücksichtigen Sie bei der Lösung, dass das äquivalente Tiefpass-Signal auch in der Form
- $$s_{\rm TP}(t) = a(t) \cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \phi(t)} $$
dargestellt werden kann, wobei $a(t) ≥ 0$ gelten soll. Für $\phi(t)$ ist der Wertebereich $–\pi < \phi(t) \leq +\pi$ zulässig und es gilt die allgemeingültige Gleichung:
- $$\phi(t)= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\big[s_{\rm TP}(t)\big]}{{\rm Re}\big[s_{\rm TP}(t)\big]}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Äquivalentes Tiefpass-Signal und zugehörige Spektralfunktion.
- Sie können Ihre Lösung mit dem interaktiven Applet Physikalisches Signal & Äquivalentes Tiefpass-Signal ⇒ „Ortskurve” überprüfen.
Fragebogen
Musterlösung
(1) Verschiebt man alle Diraclinien jeweils um $f_{\rm T} = 50 \ \text{kHz}$ nach links, so liegen diese bei $-\hspace{-0.08cm}10 \ \text{kHz}$, $0$ und $+10 \ \text{kHz}$.
- Die Gleichung für $s_{\rm TP}(t)$ lautet mit $\omega_{10} = 2 \pi \cdot 10 \ \text{kHz}$:
- $$s_{\rm TP}(t) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }+{\rm j}\cdot {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \omega_{\rm 10} \hspace{0.05cm} t }$$
- $$\Rightarrow \hspace{0.3cm} s_{\rm TP}(t = 0) = {\rm 1 \hspace{0.05cm} V} - {\rm j}\cdot {\rm 1 \hspace{0.05cm} V} +{\rm j}\cdot {\rm 1 \hspace{0.05cm} V}= {\rm 1 \hspace{0.05cm} V}.$$
- $$\Rightarrow \hspace{0.3cm} {\rm Re}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= {+\rm 1 \hspace{0.05cm} V}}, \hspace{0.2cm}{\rm Im}[s_{\rm TP}(t = 0) ] \hspace{0.15 cm}\underline{= 0} .$$
(2) Obige Gleichung kann man nach dem Satz von Euler mit $T_0 = 1/f_{\rm N} = 100 \ {\rm µ} \text{s}$ wie folgt umformen:
- $$\frac{s_{\rm TP}(t)}{{\rm 1 \hspace{0.05cm} V}}\hspace{-0.05cm} =\hspace{-0.05cm}1\hspace{-0.05cm} - \hspace{-0.05cm}{\rm j}\cdot \cos({ \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm} \sin({ \omega_{\rm 10}\hspace{0.05cm} t }) \hspace{-0.05cm}+\hspace{-0.05cm}{\rm j}\cdot \cos({ \omega_{\rm 10}\hspace{0.05cm} t })\hspace{-0.05cm} + \hspace{-0.05cm} \sin({ \omega_{\rm 10}\hspace{0.05cm} t }) = 1+2 \cdot \sin(2 \pi {t}/{T_0}) .$$
- Damit ist gezeigt, dass $s_{\rm TP}(t)$ für alle Zeiten $t$ reell ist.
- Für die gesuchten Zahlenwerte erhält man:
- $$s_{\rm TP}(t = {\rm 10 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(36^\circ)\right]\hspace{0.15 cm}\underline{={{\rm +2.176 \hspace{0.05cm} V}}},$$
- $$s_{\rm TP}(t = {\rm 25 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(90^\circ)\right]\hspace{0.15 cm}\underline{={{\rm +3 \hspace{0.05cm} V}}},$$
- $$s_{\rm TP}(t = {\rm 75 \hspace{0.1cm} {\rm µ} s}) = {\rm 1 \hspace{0.05cm} V} \cdot \left[1+2 \cdot \sin(270^\circ)\right]\hspace{0.15 cm}\underline{= -{{\rm 1 \hspace{0.05cm} V}}},$$
- $$s_{\rm TP}(t = {\rm 100 \hspace{0.1cm}{\rm µ} s}) = s_{\rm TP}(t = 0) \hspace{0.15 cm}\underline{={{\rm +1 \hspace{0.05cm} V}}}.$$
(3) Definitionsgemäß gilt $a(t) = |s_{\rm TP}(t)|$. Damit erhält man folgende Zahlenwerte:
- $$a(t = {\rm 25 \hspace{0.1cm} {\rm µ} s}) = s_{\rm TP}(t = {\rm 25 \hspace{0.05cm}{\rm µ} s}) \hspace{0.15 cm}\underline{= {\rm +3 \hspace{0.05cm} V}} , \hspace{4.15 cm}$$
- $$a(t = {\rm 75 \hspace{0.1cm} {\rm µ} s}) = |s_{\rm TP}(t = {\rm 75 \hspace{0.05cm} {\rm µ} s})| \hspace{0.15 cm}\underline{= {\rm +1 \hspace{0.05cm} V}} .$$
(4) Allgemein gilt für die Phasenfunktion:
- $$\phi(t)= {\rm arc} \left[s_{\rm TP}(t)\right]= {\rm arctan} \hspace{0.1cm}\frac{{\rm Im}\left[s_{\rm TP}(t)\right]}{{\rm Re}\left[s_{\rm TP}(t)\right]}$$
Aufgrund der Tatsache, dass hier für alle Zeiten ${\rm Im}[s_{\rm TP}(t)] = 0$ ist, erhält man hieraus das Ergebnis:
- Falls ${\rm Re}[s_{\rm TP}(t)] > 0$ gilt, ist die Phase $\phi(t) = 0$.
- Dagegen gilt bei negativem Realteil: $\phi(t) = \pi$.
Wir beschränken uns hier auf den Zeitbereich einer Periode: $0 \leq t \leq T_0$.
- Im Bereich zwischen $t_1$ und $t_2$ liegt eine Phase von $180^\circ$ vor, ansonsten gilt $\text{Re}[s_{\rm TP}(t)] \geq 0$.
- Zur Berechung von $t_1$ kann das Ergebnis der Teilaufgabe (2) herangezogen werden:
- $$\sin(2 \pi \cdot {t_1}/{T_0}) = -0.5 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2 \pi \cdot {t_1}/{T_0} = 2 \pi \cdot {7}/{12}\hspace{0.3cm}{\rm (entspricht}\hspace{0.2cm}210^\circ )$$
- Daraus erhält man $t_1 = 7/12 · T_0 = 58.33 \ {\rm µ} \text{s}$.
- Durch ähnliche Überlegungen kommt man zum Ergebnis: $t_2 = 11/12 · T_0 = 91.63 \ {\rm µ} \text{s}$.
Die gesuchten Werte sind somit:
- $$\phi(t = 25 \ {\rm µ} \text{s}) \; \underline { = 0},$$
- $$\phi(t = 75 \ {\rm µ} \text{s}) \; \underline { = 180^{\circ}}\; (= \pi).$$