Lineare zeitinvariante Systeme/Nichtlineare Verzerrungen: Unterschied zwischen den Versionen
David (Diskussion | Beiträge) |
|||
| (25 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
|Nächste Seite=Lineare Verzerrungen | |Nächste Seite=Lineare Verzerrungen | ||
}} | }} | ||
| + | |||
==Eigenschaften nichtlinearer Systeme== | ==Eigenschaften nichtlinearer Systeme== | ||
| − | + | <br> | |
| + | Die Systembeschreibung mittels des Frequenzgangs $H(f)$ und/oder der Impulsantwort $h(t)$ ist nur bei einem [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Frequenzbereich#.C3.9Cbertragungsfunktion_-_Frequenzgang|LZI–System]] möglich. Beinhaltet aber das System auch nichtlineare Komponenten wie es für dieses Kapitel vorausgesetzt wird, so sind kein Frequenzgang und auch keine Impulsantwort angebbar und das Modell muss allgemeiner gestaltet werden. | ||
| + | |||
| + | [[Datei:P_ID887__LZI_T_2_2_S1_neu.png |frame| Beschreibung eines nichtlinearen Systems|class=fit]] | ||
| − | + | Auch bei diesem nichtlinearen Systemen bezeichnen wir die Signale am Eingang und Ausgang mit $x(t)$ bzw. $y(t)$ und die dazugehörigen Spektralfunktionen mit $X(f)$ und $Y(f)$. | |
| − | + | Ein Beobachter wird hier Folgendes feststellen: | |
| − | *Die Übertragungseigenschaften sind nun auch von der Größe des Eingangssignals abhängig. Führt $x(t)$ zum Ausgangssignal $y(t)$, so kann daraus nun nicht mehr geschlossen werden, dass sich beim Eingangssignal $K · x(t)$ stets das Signal $K · y(t)$ ergeben wird. | + | *Die Übertragungseigenschaften sind nun auch '''von der Größe des Eingangssignals abhängig''' . Führt $x(t)$ zum Ausgangssignal $y(t)$, so kann daraus nun nicht mehr geschlossen werden, dass sich beim Eingangssignal $K · x(t)$ stets das Signal $K · y(t)$ ergeben wird. |
| − | *Das bedeutet | + | *Das bedeutet auch, dass das '''Superpositionsprinzip nicht mehr anwendbar ist''', mit der Konsequenz, dass aus den Korrespondenzen $x_1(t) ⇒ y_1(t)$ und $x_2(t) ⇒ y_2(t)$ nicht auf das Ergebnis $x_1(t) + x_2(t) ⇒ y_1(t) + y_2(t)$ geschlossen werden kann. |
| − | *Durch Nichtlinearitäten entstehen neue Frequenzen. Ist $x(t)$ eine harmonische Schwingung mit der Frequenz $f_0$, so beinhaltet das Ausgangssignal $y(t)$ auch Anteile bei Vielfachen von $f_0$. Diese bezeichnet man in der Nachrichtentechnik als Oberwellen. | + | *Durch Nichtlinearitäten '''entstehen neue Frequenzen'''. Ist $x(t)$ eine harmonische Schwingung mit der Frequenz $f_0$, so beinhaltet das Ausgangssignal $y(t)$ auch Anteile bei Vielfachen von $f_0$. Diese bezeichnet man in der Nachrichtentechnik als '''Oberwellen'''. |
| − | *Ein Nachrichtensignal beinhaltet in der Praxis meist sehr viele Frequenzanteile. Die Oberwellen der niederfrequenten Signalanteile fallen nun in den Bereich höherfrequenter Nutzanteile. Dadurch ergeben sich nichtreversible Signalverfälschungen. | + | *Ein Nachrichtensignal beinhaltet in der Praxis meist sehr viele Frequenzanteile. Die Oberwellen der niederfrequenten Signalanteile fallen nun in den Bereich höherfrequenter Nutzanteile. Dadurch ergeben sich '''nichtreversible Signalverfälschungen'''. |
| − | Bevor am | + | Bevor wir am Abschnittsende [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Konstellationen.2C_die_zu_nichtlinearen_Verzerrungen_f.C3.BChren|„Konstellationen, die zu nichtlinearen Verzerrungen führen”]] nennen, wird das Problem der nichtlinearen Verzerrungen mathematisch erfasst. |
| + | *Wir setzen dabei voraus, dass '''das System kein Gedächtnis besitzt''', so dass der Ausgangswert $y = y(t_0)$ nur vom momentanen Eingangswert $x = x(t_0)$ abhängt, | ||
| + | *nicht aber vom Signalverlauf $x(t)$ für $t < t_0$. | ||
| − | ==Beschreibung nichtlinearer Systeme | + | ==Beschreibung nichtlinearer Systeme== |
| − | {{Definition} | + | <br> |
| − | Ein System bezeichnet man als nichtlinear, wenn | + | {{BlaueBox|TEXT= |
| + | $\text{Definition:}$ | ||
| + | Ein System bezeichnet man als '''nichtlinear''', wenn zwischen dem Signalwert $x = x(t)$ am Eingang und dem Ausgang $y = y(t)$ der folgende Zusammenhang besteht: | ||
$$y = g(x) \ne {\rm const.} \cdot x.$$ | $$y = g(x) \ne {\rm const.} \cdot x.$$ | ||
| − | Man bezeichnet den Verlauf $y = g(x)$ als die nichtlineare Kennlinie des Systems. | + | Man bezeichnet den Verlauf $y = g(x)$ als die '''nichtlineare Kennlinie''' des Systems.}} |
| − | + | ||
| + | |||
| + | [[Datei:P_ID888__LZI_T_2_2_S2_neu.png |right|frame| Nichtlineare Kennlinie|class=fit]] | ||
| + | |||
| + | *In der Grafik ist beispielhaft als grüne Kurve die nichtlineare Kennlinie $y = g(x)$ zu erkennen, die entsprechend dem ersten Viertel einer Sinusfunktion geformt ist. | ||
| + | *In roter Farbe gestrichelt erkennt man den Sonderfall eines linearen Systems mit der Kennlinie $y = x$. | ||
| − | |||
| − | + | Da jede Kennlinie um den Arbeitspunkt in eine Taylorreihe entwickelt werden kann, lässt sich das Ausgangssignal auch wie folgt darstellen: | |
| + | $$y(t) = \sum_{i=0}^{\infty}\hspace{0.1cm} c_i \cdot x^{i}(t) = c_0 + c_1 \cdot x(t) + c_2 \cdot x^{2}(t) + c_3 \cdot x^{3}(t) + \hspace{0.05cm}\text{...}$$ | ||
| + | Besitzt $x(t)$ eine Einheit – zum Beispiel „Volt”, so sind auch die Koeffizienten der Taylorreihe mit Einheiten anzusetzen und zwar mit unterschiedlichen: | ||
| + | *$c_0$ mit $\rm V$, | ||
| + | *$c_1$ ohne Einheit, | ||
| + | *$c_2$ mit $\rm 1/V$, usw.. | ||
| − | |||
| − | |||
| − | |||
| − | In obiger Grafik ist der Arbeitspunkt identisch mit dem Nullpunkt und es gilt $c_0 = 0$. | + | In obiger Grafik ist der Arbeitspunkt identisch mit dem Nullpunkt und es gilt $c_0 = 0$. |
| − | = | + | {{GraueBox|TEXT= |
| − | + | $\text{Beispiel 1:}$ | |
| − | Die auf der ersten Seite dieses Abschnitts aufgelisteten Eigenschaften nichtlinearer Systeme werden hier anhand der Kennlinie $y = g(x) = | + | Die auf der [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Eigenschaften_nichtlinearer_Systeme|ersten Seite dieses Abschnitts]] aufgelisteten Eigenschaften nichtlinearer Systeme werden hier anhand der Kennlinie $y = g(x) = \sin(x)$ verdeutlicht, die in der Mitte der Grafik dargestellt ist. |
| + | *Das Gleichsignal $x(t) = 0.5$ hat hier das konstante Ausgangssignal $y(t) = 0.479$ zur Folge. | ||
| + | * Mit $x(t) = 1$ ergibt sich das Ausgangssignal zu $y(t) = 0.841 ≠ 2 · 0.479$. | ||
| + | *Durch eine Verdopplung von $x(t)$ wird hier also nicht auch gleichzeitig $y(t)$ verdoppelt ⇒ das Superpositionsprinzip wird verletzt. | ||
| − | |||
| − | + | [[Datei:P_ID889__LZI_T_2_2_S2b_neu.png|center|frame| Auswirkungen einer nichtlinearen Kennlinie|class=fit]] | |
| − | + | Die äußeren Grafiken zeigen – jeweils in blau – cosinusförmige Eingangssignale $x(t)$ mit unterschiedlichen Amplituden $A$ und in rot die dazugehörigen verzerrten Ausgangssignale $y(t)$. Man erkennt die Zunahme der nichtlinearen Verzerrungen mit größer werdender Amplitude, die durch den auf der nächsten Seite definierten Klirrfaktor $K$ quantifiziert werden. | |
| − | + | *Das rechte obere Diagramm für $A = 1.5$ zeigt eindeutig, dass nun $y(t)$ nicht mehr cosinusförmig ist; die Halbwellen verlaufen runder als bei der Cosinusfunktion. | |
| − | + | *Aber auch für $A = 0.5$ und $A = 1.0$ weichen – wenn auch weniger stark – die Signale $y(t)$ aufgrund von Oberwellen von der Cosinusform ab. Das heißt, es entstehen neue Frequenzanteile bei Vielfachen der Cosinusfrequenz $f_0$. | |
| − | + | *Im rechten unteren Bild wird durch einen zusätzlichen Gleichanteil die Kennlinie nur einseitig betrieben. Man erkennt nun auch eine Unsymmetrie im Signal $y(t)$. Die untere Halbwelle verläuft spitzförmiger als die obere. Der Klirrfaktor beträgt hier $K \approx 22\%$.}} | |
| − | |||
| − | + | ==Der Klirrfaktor== | |
| + | <br> | ||
| + | Zur quantitativen Erfassung der nichtlinearen Verzerrungen gehen wir von einem cosinusförmigen Eingangssignal $x(t)$ mit Amplitude $A_x$ aus. | ||
| + | [[Datei:LZI_T_2_2_S3_vers2.png|center|frame|Zur Definition des Klirrfaktors|class=fit]] | ||
| + | |||
Das Ausgangssignal beinhaltet aufgrund der nichtlinearen Verzerrungen Oberwellen und es gilt allgemein: | Das Ausgangssignal beinhaltet aufgrund der nichtlinearen Verzerrungen Oberwellen und es gilt allgemein: | ||
$$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + | $$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + | ||
| − | A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm} | + | A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm}\text{...}$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | Mit diesen Amplitudenwerten $A_i$ lautet die Gleichung für den '''Klirrfaktor''': | ||
| + | :$$K = \frac {\sqrt{A_2^2+ A_3^2+ A_4^2+ \hspace{0.05cm}\text{...} } }{A_1} = \sqrt{K_2^2+ | ||
| + | K_3^2+K_4^2+ \hspace{0.05cm}\text{...} }.$$ | ||
| + | In der zweiten Gleichung bezeichnet | ||
| + | *$K_2 = A_2/A_1$ den Klirrfaktor zweiter Ordnung, | ||
| + | *$K_3 = A_3/A_1$ den Klirrfaktor dritter Ordnung usw.}} | ||
| − | |||
| − | + | Ausdrücklich wird darauf hingewiesen, dass bei der Berechnung des Klirrfaktors die Amplitude $A_x$ des Eingangssignals nicht berücksichtigt wird. Auch ein entstehender Gleichanteil $A_0$ bleibt unberücksichtigt. | |
| − | + | Im [[Lineare_zeitinvariante_Systeme/Nichtlineare_Verzerrungen#Beschreibung_nichtlinearer_Systeme|$\text{Beispiel 1}$]] im letzten Abschnitt wurden die Klirrfaktoren mit Werten zwischen etwa $1\%$ und $20\%$ angegeben. | |
| − | + | *Diese Werte liegen schon deutlich über den Klirrfaktoren preisgünstiger Audioanlagen, für die $K < 0.1\%$ gilt. | |
| − | + | *Bei HiFi–Geräten wird auf die Linearität besonderer Wert gelegt und ein sehr kleiner Klirrfaktor schlägt sich auch im Preis nieder. | |
| − | |||
| − | |||
| − | [[ | + | Ein Vergleich mit der Seite [[Lineare_zeitinvariante_Systeme/Klassifizierung_der_Verzerrungen#Ber.C3.BCcksichtigung_von_D.C3.A4mpfung_und_Laufzeit|Berücksichtigung von Dämpfung und Laufzeit]] lässt erkennen, dass für den Sonderfall eines cosinusförmigem Eingangssignals das dort definierte Signal–zu–Verzerrungs–Leistungsverhältnis gleich dem Kehrwert des Klirrfaktors zum Quadrat ist: |
| + | :$$\rho_{\rm V} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} = \left(\frac{ A_{1}}{A_x} \right)^2 \cdot | ||
| + | \frac{ {1}/{2} \cdot A_{x}^2}{{1}/{2} \cdot (A_{2}^2 + A_{3}^2 + A_{4}^2 + \hspace{0.05cm}...) } = \frac{1}{K^2}\hspace{0.05cm}.$$ | ||
| + | [[Datei:P_ID1090__LZI_T_2_2_S3b_neu.png |frame|Einfluss einer Nichtlinearität auf ein Cosinussignal | right|class=fit]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
Wir betrachten nun ein mittelwertbehaftetes Cosinussignal: | Wir betrachten nun ein mittelwertbehaftetes Cosinussignal: | ||
| − | $$x(t) = | + | :$$x(t) = {1}/{2} + {1}/{2}\cdot \cos (\omega_0 \cdot t).$$ |
| − | + | $x(t)$ nimmt Werte zwischen $0$ und $1$ an und ist als blaue Kurve gezeichnet. Die Signalleistung ist | |
| + | :$$P_x = 1/4 + 1/8 = 0.375.$$ | ||
Gibt man dieses Signal auf eine Nichtlinearität mit der Kennlinie | Gibt man dieses Signal auf eine Nichtlinearität mit der Kennlinie | ||
| − | $$y=g(x) = \sin(x) \approx x - | + | :$$y=g(x) = \sin(x) \approx x - {x^3}/{6} \hspace{0.05cm},$$ |
so lautet das Ausgangssignal: | so lautet das Ausgangssignal: | ||
| − | $$y(t) = A_0 + A_1 \cdot \cos (\omega_0 \cdot t)+ A_2 \cdot \cos (2\omega_0 \cdot t)+ A_3 \cdot \cos (3\omega_0 \cdot t)\hspace{0.05cm},$$ | + | :$$y(t) = A_0 + A_1 \cdot \cos (\omega_0 \cdot t)+ A_2 \cdot \cos (2\omega_0 \cdot t)+ A_3 \cdot \cos (3\omega_0 \cdot t)\hspace{0.05cm},$$ |
| − | $$A_0 = | + | :$$\Rightarrow \hspace{0.3cm} A_0 = {86}/{192},\hspace{0.3cm}A_1 = {81}/{192},\hspace{0.3cm}A_2 = - {6}/{192},\hspace{0.3cm}A_3 = - |
| − | {1}{192} | + | {1}/{192}\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | |||
| − | + | Zur Berechnung der Fourierkoeffizienten wurden die trigonometrischen Umformungen für $\cos^2(α)$ und $\cos^3(α)$ verwendet. Der Klirrfaktor ergibt sich damit zu | |
| + | :$$K = \frac {\sqrt{A_2^{\hspace{0.05cm}2} + A_3^{\hspace{0.05cm}2} } }{A_1}\approx 7.5\%\hspace{0.05cm}.$$ | ||
| + | Man erkennt weiter, dass das rot skizzierte Signal $y(t)$ nahezu gleich dem grün gezeichneten Signal $α · x(t)$ mit $α = \sin(1) ≈ 5/6$ ist. | ||
| − | Definiert man das Fehlersignal $ε_1(t) = y(t) | + | Definiert man das Fehlersignal $ε_1(t) = y(t) - α · x(t)$, so ergibt sich mit dessen Leistung |
| − | $$P_{\varepsilon 1} = \frac {(80-86)^2}{192^2} + \frac {6^2 + (-1)^2}{2 \cdot 192^2}\approx 1.48 \cdot 10^{-3}$$ | + | :$$P_{\varepsilon 1} = \frac {(80-86)^2}{192^2} + \frac {6^2 + (-1)^2}{2 \cdot 192^2}\approx 1.48 \cdot 10^{-3}$$ |
für das Signal–zu–Stör–Leistungsverhältnis: | für das Signal–zu–Stör–Leistungsverhältnis: | ||
| − | $$\rho_{ | + | :$$\rho_{{\rm V} 1} = \frac {\alpha^2 \cdot P_x}{P_{\varepsilon 1} } = \frac {(5/6)^2 \cdot 0.375}{1.48 \cdot 10^{-3} }\approx |
| − | 176 = | + | 176 = {1}/{K^2}\hspace{0.05cm}.$$ |
| + | Dagegen ist das SNR deutlich geringer, wenn man den Dämpfungsfaktor $α$ nicht berücksichtigt, das heißt, wenn man vom Fehlersignal $ε_2 = y(t) - x(t)$ ausgeht: | ||
| + | :$$P_{\varepsilon 2} = \frac {(86-96)^2}{192^2} + \frac {(81-96)^2 + 6^2 + (-1)^2}{2 \cdot 192^2}\approx 6.3 \cdot 10^{-3} \hspace{0.3cm} | ||
| + | \Rightarrow | ||
| + | \hspace{0.3cm}\rho_{{\rm V} 2} = \frac { P_x}{P_{\varepsilon 2}}= \frac {0.375}{6.3 \cdot 10^{-3}} | ||
| + | \approx 60 \hspace{0.05cm}.$$}} | ||
| − | + | ==Rauschklirrmessung== | |
| − | + | <br> | |
| − | + | Ein großer Nachteil der Klirrfaktordefinition ist die damit einhergehende Festlegung auf cosinusförmige Testsignale, also auf realitätsferne Bedingungen. | |
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:P_ID892__LZI_T_2_2_S4_neu.png |right|frame| Prinzip der Rauschklirrmessung|class=fit]] | |
| − | + | ||
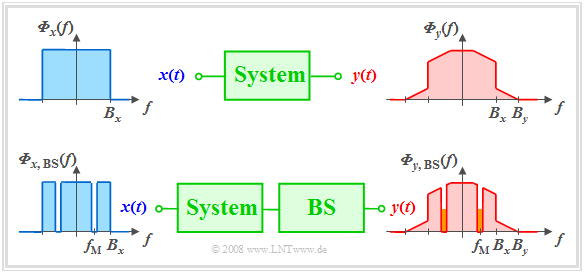
| + | *Bei der so genannten Rauschklirrmessung modelliert man das zu übertragende Signal $x(t)$ durch weißes Rauschen mit der Rauschleistungsdichte ${\it \Phi}_x(f)$. | ||
| + | *Zusätzlich bringt man in das System eine schmale Bandsperre $\rm (BS)$ mit Mittelfrequenz $f_{\rm M}$ und (sehr kleiner) Bandbreite $B_{\rm BS}$ ein. | ||
| − | |||
| − | Bei einem linearen System wäre das Ausgangsspektrum $ | + | Bei einem linearen System wäre das Ausgangsspektrum ${\it \Phi}_y(f)$ nicht breiter als $B_x$ und auch im Bereich um $f_{\rm M}$ gäbe es keine Anteile. |
| − | + | Diese ergeben sich allein durch Mischprodukte (Intermodulationsanteile) verschiedener Spektralanteile, also durch nichtlineare Verzerrungen. | |
| + | Durch Variation der Mittenfrequenz $f_{\rm M}$ und Integration über alle diese kleinen Störanteile kann somit die Verzerrungsleistung ermittelt werden. Nähere Angaben zu dieser Methode findet man zum Beispiel in [Kam04]<ref>Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.</ref>. | ||
| + | <br clear=all> | ||
==Konstellationen, die zu nichtlinearen Verzerrungen führen== | ==Konstellationen, die zu nichtlinearen Verzerrungen führen== | ||
| − | Als Beispiel für das Auftreten nichtlinearer Verzerrungen bei analogen Nachrichtenübertragungssystemen sollen hier einige Konstellationen genannt werden, die zu solchen führen. Inhaltlich bedeutet dies einen Vorgriff auf das Buch | + | <br> |
| + | Als Beispiel für das Auftreten nichtlinearer Verzerrungen bei analogen Nachrichtenübertragungssystemen sollen hier einige Konstellationen genannt werden, die zu solchen führen. Inhaltlich bedeutet dies einen Vorgriff auf das Buch [[Modulationsverfahren]]. | ||
| + | |||
| + | [[Datei:P_ID893__LZI_T_2_2_S5_neu.png |center|frame| Allgemeines Blockschaltbild eines Nachrichtenübertragungssystems|class=fit]] | ||
| + | |||
| + | Nichtlineare Verzerrungen des Sinkensignals $v(t)$ in Bezug zum Quellensignal $q(t)$ treten auf, wenn | ||
| + | *es bereits auf dem Kanal – also bezüglich des Sendesignals $s(t)$ und des Empfangssignals $r(t)$ – zu nichtlinearen Verzerrungen kommt, | ||
| + | *bei der [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#ZSB-Amplitudenmodulation_mit_Tr.C3.A4ger|Zweiseitenband–Amplitudenmodulation]] (ZSB–AM) mit Modulationsgrad $m > 1$ ein Hüllkurvendemodulator verwendet wird, | ||
| + | *bei ZSB–AM und Hüllkurvendemodulation ein linear verzerrender Kanal vorliegt und zwar auch bei einem Modulationsgrad $m < 1$, | ||
| + | *man die Kombination Einseitenband–AM und [[Modulationsverfahren/Hüllkurvendemodulation|Hüllkurvendemodulation]] verwendet (unabhängig vom Seitenband–zu–Träger–Verhältnis), | ||
| + | *eine [[Modulationsverfahren/Phasenmodulation_(PM)#Gemeinsamkeiten_zwischen_Phasen.E2.80.93_und_Frequenzmodulation|Winkelmodulation]] (Oberbegriff für Frequenz– und Phasenmodulation) angewandt wird und die zur Verfügung stehende Bandbreite nur endlich groß ist. | ||
| + | |||
| + | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:2.3_Sinusförmige_Kennlinie| Aufgabe 2.3: Sinusförmige Kennlinie]] | ||
| + | |||
| + | [[Aufgaben:2.3Z_Kennlinienbetrieb_asymmetrisch|Aufgabe 2.3Z: Kennlinienbetrieb asymmetrisch]] | ||
| + | |||
| + | [[Aufgaben:2.4_Klirrfaktor_und_Verzerrungsleistung|Aufgabe 2.4: Klirrfaktor und Verzerrungsleistung]] | ||
| + | |||
| + | [[2.4Z_Kennlinienvermessung|Aufgabe 2.4Z: Kennlinienvermessung]] | ||
| + | |||
| + | {{Display}} | ||
| − | + | ==Quellenverzeichnis== | |
| + | <references/> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 28. September 2021, 17:40 Uhr
Inhaltsverzeichnis
Eigenschaften nichtlinearer Systeme
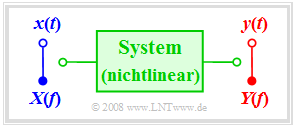
Die Systembeschreibung mittels des Frequenzgangs $H(f)$ und/oder der Impulsantwort $h(t)$ ist nur bei einem LZI–System möglich. Beinhaltet aber das System auch nichtlineare Komponenten wie es für dieses Kapitel vorausgesetzt wird, so sind kein Frequenzgang und auch keine Impulsantwort angebbar und das Modell muss allgemeiner gestaltet werden.
Auch bei diesem nichtlinearen Systemen bezeichnen wir die Signale am Eingang und Ausgang mit $x(t)$ bzw. $y(t)$ und die dazugehörigen Spektralfunktionen mit $X(f)$ und $Y(f)$.
Ein Beobachter wird hier Folgendes feststellen:
- Die Übertragungseigenschaften sind nun auch von der Größe des Eingangssignals abhängig . Führt $x(t)$ zum Ausgangssignal $y(t)$, so kann daraus nun nicht mehr geschlossen werden, dass sich beim Eingangssignal $K · x(t)$ stets das Signal $K · y(t)$ ergeben wird.
- Das bedeutet auch, dass das Superpositionsprinzip nicht mehr anwendbar ist, mit der Konsequenz, dass aus den Korrespondenzen $x_1(t) ⇒ y_1(t)$ und $x_2(t) ⇒ y_2(t)$ nicht auf das Ergebnis $x_1(t) + x_2(t) ⇒ y_1(t) + y_2(t)$ geschlossen werden kann.
- Durch Nichtlinearitäten entstehen neue Frequenzen. Ist $x(t)$ eine harmonische Schwingung mit der Frequenz $f_0$, so beinhaltet das Ausgangssignal $y(t)$ auch Anteile bei Vielfachen von $f_0$. Diese bezeichnet man in der Nachrichtentechnik als Oberwellen.
- Ein Nachrichtensignal beinhaltet in der Praxis meist sehr viele Frequenzanteile. Die Oberwellen der niederfrequenten Signalanteile fallen nun in den Bereich höherfrequenter Nutzanteile. Dadurch ergeben sich nichtreversible Signalverfälschungen.
Bevor wir am Abschnittsende „Konstellationen, die zu nichtlinearen Verzerrungen führen” nennen, wird das Problem der nichtlinearen Verzerrungen mathematisch erfasst.
- Wir setzen dabei voraus, dass das System kein Gedächtnis besitzt, so dass der Ausgangswert $y = y(t_0)$ nur vom momentanen Eingangswert $x = x(t_0)$ abhängt,
- nicht aber vom Signalverlauf $x(t)$ für $t < t_0$.
Beschreibung nichtlinearer Systeme
$\text{Definition:}$ Ein System bezeichnet man als nichtlinear, wenn zwischen dem Signalwert $x = x(t)$ am Eingang und dem Ausgang $y = y(t)$ der folgende Zusammenhang besteht: $$y = g(x) \ne {\rm const.} \cdot x.$$ Man bezeichnet den Verlauf $y = g(x)$ als die nichtlineare Kennlinie des Systems.
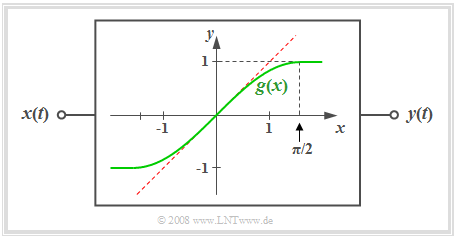
- In der Grafik ist beispielhaft als grüne Kurve die nichtlineare Kennlinie $y = g(x)$ zu erkennen, die entsprechend dem ersten Viertel einer Sinusfunktion geformt ist.
- In roter Farbe gestrichelt erkennt man den Sonderfall eines linearen Systems mit der Kennlinie $y = x$.
Da jede Kennlinie um den Arbeitspunkt in eine Taylorreihe entwickelt werden kann, lässt sich das Ausgangssignal auch wie folgt darstellen: $$y(t) = \sum_{i=0}^{\infty}\hspace{0.1cm} c_i \cdot x^{i}(t) = c_0 + c_1 \cdot x(t) + c_2 \cdot x^{2}(t) + c_3 \cdot x^{3}(t) + \hspace{0.05cm}\text{...}$$ Besitzt $x(t)$ eine Einheit – zum Beispiel „Volt”, so sind auch die Koeffizienten der Taylorreihe mit Einheiten anzusetzen und zwar mit unterschiedlichen:
- $c_0$ mit $\rm V$,
- $c_1$ ohne Einheit,
- $c_2$ mit $\rm 1/V$, usw..
In obiger Grafik ist der Arbeitspunkt identisch mit dem Nullpunkt und es gilt $c_0 = 0$.
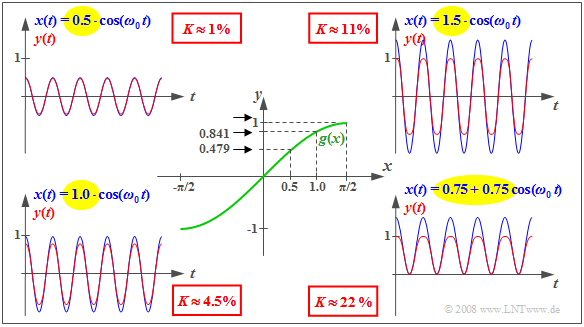
$\text{Beispiel 1:}$ Die auf der ersten Seite dieses Abschnitts aufgelisteten Eigenschaften nichtlinearer Systeme werden hier anhand der Kennlinie $y = g(x) = \sin(x)$ verdeutlicht, die in der Mitte der Grafik dargestellt ist.
- Das Gleichsignal $x(t) = 0.5$ hat hier das konstante Ausgangssignal $y(t) = 0.479$ zur Folge.
- Mit $x(t) = 1$ ergibt sich das Ausgangssignal zu $y(t) = 0.841 ≠ 2 · 0.479$.
- Durch eine Verdopplung von $x(t)$ wird hier also nicht auch gleichzeitig $y(t)$ verdoppelt ⇒ das Superpositionsprinzip wird verletzt.
Die äußeren Grafiken zeigen – jeweils in blau – cosinusförmige Eingangssignale $x(t)$ mit unterschiedlichen Amplituden $A$ und in rot die dazugehörigen verzerrten Ausgangssignale $y(t)$. Man erkennt die Zunahme der nichtlinearen Verzerrungen mit größer werdender Amplitude, die durch den auf der nächsten Seite definierten Klirrfaktor $K$ quantifiziert werden.
- Das rechte obere Diagramm für $A = 1.5$ zeigt eindeutig, dass nun $y(t)$ nicht mehr cosinusförmig ist; die Halbwellen verlaufen runder als bei der Cosinusfunktion.
- Aber auch für $A = 0.5$ und $A = 1.0$ weichen – wenn auch weniger stark – die Signale $y(t)$ aufgrund von Oberwellen von der Cosinusform ab. Das heißt, es entstehen neue Frequenzanteile bei Vielfachen der Cosinusfrequenz $f_0$.
- Im rechten unteren Bild wird durch einen zusätzlichen Gleichanteil die Kennlinie nur einseitig betrieben. Man erkennt nun auch eine Unsymmetrie im Signal $y(t)$. Die untere Halbwelle verläuft spitzförmiger als die obere. Der Klirrfaktor beträgt hier $K \approx 22\%$.
Der Klirrfaktor
Zur quantitativen Erfassung der nichtlinearen Verzerrungen gehen wir von einem cosinusförmigen Eingangssignal $x(t)$ mit Amplitude $A_x$ aus.
Das Ausgangssignal beinhaltet aufgrund der nichtlinearen Verzerrungen Oberwellen und es gilt allgemein: $$y(t) = A_0 + A_1 \cdot \cos(\omega_0 t) + A_2 \cdot \cos(2\omega_0 t) + A_3 \cdot \cos(3\omega_0 t) + \hspace{0.05cm}\text{...}$$
$\text{Definition:}$ Mit diesen Amplitudenwerten $A_i$ lautet die Gleichung für den Klirrfaktor:
- $$K = \frac {\sqrt{A_2^2+ A_3^2+ A_4^2+ \hspace{0.05cm}\text{...} } }{A_1} = \sqrt{K_2^2+ K_3^2+K_4^2+ \hspace{0.05cm}\text{...} }.$$
In der zweiten Gleichung bezeichnet
- $K_2 = A_2/A_1$ den Klirrfaktor zweiter Ordnung,
- $K_3 = A_3/A_1$ den Klirrfaktor dritter Ordnung usw.
Ausdrücklich wird darauf hingewiesen, dass bei der Berechnung des Klirrfaktors die Amplitude $A_x$ des Eingangssignals nicht berücksichtigt wird. Auch ein entstehender Gleichanteil $A_0$ bleibt unberücksichtigt.
Im $\text{Beispiel 1}$ im letzten Abschnitt wurden die Klirrfaktoren mit Werten zwischen etwa $1\%$ und $20\%$ angegeben.
- Diese Werte liegen schon deutlich über den Klirrfaktoren preisgünstiger Audioanlagen, für die $K < 0.1\%$ gilt.
- Bei HiFi–Geräten wird auf die Linearität besonderer Wert gelegt und ein sehr kleiner Klirrfaktor schlägt sich auch im Preis nieder.
Ein Vergleich mit der Seite Berücksichtigung von Dämpfung und Laufzeit lässt erkennen, dass für den Sonderfall eines cosinusförmigem Eingangssignals das dort definierte Signal–zu–Verzerrungs–Leistungsverhältnis gleich dem Kehrwert des Klirrfaktors zum Quadrat ist:
- $$\rho_{\rm V} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} = \left(\frac{ A_{1}}{A_x} \right)^2 \cdot \frac{ {1}/{2} \cdot A_{x}^2}{{1}/{2} \cdot (A_{2}^2 + A_{3}^2 + A_{4}^2 + \hspace{0.05cm}...) } = \frac{1}{K^2}\hspace{0.05cm}.$$
$\text{Beispiel 2:}$ Wir betrachten nun ein mittelwertbehaftetes Cosinussignal:
- $$x(t) = {1}/{2} + {1}/{2}\cdot \cos (\omega_0 \cdot t).$$
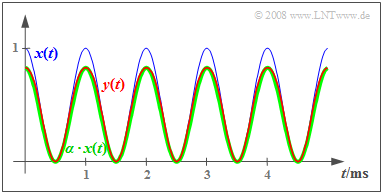
$x(t)$ nimmt Werte zwischen $0$ und $1$ an und ist als blaue Kurve gezeichnet. Die Signalleistung ist
- $$P_x = 1/4 + 1/8 = 0.375.$$
Gibt man dieses Signal auf eine Nichtlinearität mit der Kennlinie
- $$y=g(x) = \sin(x) \approx x - {x^3}/{6} \hspace{0.05cm},$$
so lautet das Ausgangssignal:
- $$y(t) = A_0 + A_1 \cdot \cos (\omega_0 \cdot t)+ A_2 \cdot \cos (2\omega_0 \cdot t)+ A_3 \cdot \cos (3\omega_0 \cdot t)\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm} A_0 = {86}/{192},\hspace{0.3cm}A_1 = {81}/{192},\hspace{0.3cm}A_2 = - {6}/{192},\hspace{0.3cm}A_3 = - {1}/{192}\hspace{0.05cm}.$$
Zur Berechnung der Fourierkoeffizienten wurden die trigonometrischen Umformungen für $\cos^2(α)$ und $\cos^3(α)$ verwendet. Der Klirrfaktor ergibt sich damit zu
- $$K = \frac {\sqrt{A_2^{\hspace{0.05cm}2} + A_3^{\hspace{0.05cm}2} } }{A_1}\approx 7.5\%\hspace{0.05cm}.$$
Man erkennt weiter, dass das rot skizzierte Signal $y(t)$ nahezu gleich dem grün gezeichneten Signal $α · x(t)$ mit $α = \sin(1) ≈ 5/6$ ist.
Definiert man das Fehlersignal $ε_1(t) = y(t) - α · x(t)$, so ergibt sich mit dessen Leistung
- $$P_{\varepsilon 1} = \frac {(80-86)^2}{192^2} + \frac {6^2 + (-1)^2}{2 \cdot 192^2}\approx 1.48 \cdot 10^{-3}$$
für das Signal–zu–Stör–Leistungsverhältnis:
- $$\rho_{{\rm V} 1} = \frac {\alpha^2 \cdot P_x}{P_{\varepsilon 1} } = \frac {(5/6)^2 \cdot 0.375}{1.48 \cdot 10^{-3} }\approx 176 = {1}/{K^2}\hspace{0.05cm}.$$
Dagegen ist das SNR deutlich geringer, wenn man den Dämpfungsfaktor $α$ nicht berücksichtigt, das heißt, wenn man vom Fehlersignal $ε_2 = y(t) - x(t)$ ausgeht:
- $$P_{\varepsilon 2} = \frac {(86-96)^2}{192^2} + \frac {(81-96)^2 + 6^2 + (-1)^2}{2 \cdot 192^2}\approx 6.3 \cdot 10^{-3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\rho_{{\rm V} 2} = \frac { P_x}{P_{\varepsilon 2}}= \frac {0.375}{6.3 \cdot 10^{-3}} \approx 60 \hspace{0.05cm}.$$
Rauschklirrmessung
Ein großer Nachteil der Klirrfaktordefinition ist die damit einhergehende Festlegung auf cosinusförmige Testsignale, also auf realitätsferne Bedingungen.
- Bei der so genannten Rauschklirrmessung modelliert man das zu übertragende Signal $x(t)$ durch weißes Rauschen mit der Rauschleistungsdichte ${\it \Phi}_x(f)$.
- Zusätzlich bringt man in das System eine schmale Bandsperre $\rm (BS)$ mit Mittelfrequenz $f_{\rm M}$ und (sehr kleiner) Bandbreite $B_{\rm BS}$ ein.
Bei einem linearen System wäre das Ausgangsspektrum ${\it \Phi}_y(f)$ nicht breiter als $B_x$ und auch im Bereich um $f_{\rm M}$ gäbe es keine Anteile.
Diese ergeben sich allein durch Mischprodukte (Intermodulationsanteile) verschiedener Spektralanteile, also durch nichtlineare Verzerrungen.
Durch Variation der Mittenfrequenz $f_{\rm M}$ und Integration über alle diese kleinen Störanteile kann somit die Verzerrungsleistung ermittelt werden. Nähere Angaben zu dieser Methode findet man zum Beispiel in [Kam04][1].
Konstellationen, die zu nichtlinearen Verzerrungen führen
Als Beispiel für das Auftreten nichtlinearer Verzerrungen bei analogen Nachrichtenübertragungssystemen sollen hier einige Konstellationen genannt werden, die zu solchen führen. Inhaltlich bedeutet dies einen Vorgriff auf das Buch Modulationsverfahren.
Nichtlineare Verzerrungen des Sinkensignals $v(t)$ in Bezug zum Quellensignal $q(t)$ treten auf, wenn
- es bereits auf dem Kanal – also bezüglich des Sendesignals $s(t)$ und des Empfangssignals $r(t)$ – zu nichtlinearen Verzerrungen kommt,
- bei der Zweiseitenband–Amplitudenmodulation (ZSB–AM) mit Modulationsgrad $m > 1$ ein Hüllkurvendemodulator verwendet wird,
- bei ZSB–AM und Hüllkurvendemodulation ein linear verzerrender Kanal vorliegt und zwar auch bei einem Modulationsgrad $m < 1$,
- man die Kombination Einseitenband–AM und Hüllkurvendemodulation verwendet (unabhängig vom Seitenband–zu–Träger–Verhältnis),
- eine Winkelmodulation (Oberbegriff für Frequenz– und Phasenmodulation) angewandt wird und die zur Verfügung stehende Bandbreite nur endlich groß ist.
Aufgaben zum Kapitel
Aufgabe 2.3: Sinusförmige Kennlinie
Aufgabe 2.3Z: Kennlinienbetrieb asymmetrisch
Aufgabe 2.4: Klirrfaktor und Verzerrungsleistung
Aufgabe 2.4Z: Kennlinienvermessung
Quellenverzeichnis
- ↑ Kammeyer, K.D.: Nachrichtenübertragung. Stuttgart: B.G. Teubner, 4. Auflage, 2004.