Aufgaben:Aufgabe 1.7: Ternäre Markovkette: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Markovketten }} right| Wir betrachten eine Markovkette mit den drei mög…“) |
|||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID453__Sto_A_1_7.png|right|]] | + | [[Datei:P_ID453__Sto_A_1_7.png|right|frame|Ternäre Markovkette]] |
| − | Wir betrachten eine Markovkette mit den drei möglichen Ereignissen $A, B | + | Wir betrachten eine Markovkette mit den drei möglichen Ereignissen $A$, $B$ und $C$: |
| + | *Die Übergangswahrscheinlichkeiten sind der Grafik zu entnehmen. | ||
| + | *Ein Übergang von $A$ nach $C$ und umgekehrt ist somit nicht möglich: | ||
| − | $p_\text{AC} = p_\text{CA} = 0 $ | + | :$$p_\text{AC} = p_\text{CA} = 0.$$ |
| − | Die drei Ereigniswahrscheinlichkeiten zum Startzeitpunkt $ | + | Die drei Ereigniswahrscheinlichkeiten zum Startzeitpunkt $\nu = 0$ sind wie folgt gegeben: |
| − | $Pr(A_0) = 0,$ | + | :$${\rm Pr}(A_0) = 0,$$ |
| + | |||
| + | :$${\rm Pr}(B_0) = 1,$$ | ||
| + | |||
| + | :$${\rm Pr}(C_0) = 0.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Markovketten|Markovketten]]. | ||
| + | *Insbesondere wird auf die Seite [[Stochastische_Signaltheorie/Markovketten#Matrix-Vektordarstellung|Matrix-Vektordarstellung]] Bezug genommen. | ||
| − | + | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie die Übergangsmatrix P und die Übergangswahrscheinlichkeiten $p_\text{AA}$, $p_\text{BB}$ und $p_\text{CC}$ an. | + | {Geben Sie die Übergangsmatrix ${\mathbf{P}}$ und die Übergangswahrscheinlichkeiten $p_\text{AA}$, $p_\text{BB}$ und $p_\text{CC}$ an. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $p_\text{AA} \ = \ $ { 0.25 3% } |
| − | $ | + | $p_\text{BB} \ = \ $ { 0. } |
| − | $ | + | $p_\text{CC} \ = \ $ { 0.75 3% } |
| − | {Berechnen Sie die Ereigniswahrscheinlichkeiten zum Zeitpunkt $ | + | {Berechnen Sie die Ereigniswahrscheinlichkeiten zum Zeitpunkt $\nu = 1$, insbesondere |
|type="{}"} | |type="{}"} | ||
| − | $Pr(A_1)$ | + | ${\rm Pr}(A_1) \ = \ $ { 0.75 3% } |
| − | {Berechnen Sie die Ereigniswahrscheinlichkeiten zum Zeitpunkt $ | + | {Berechnen Sie die Ereigniswahrscheinlichkeiten zum Zeitpunkt $\nu = 2$, insbesondere |
|type="{}"} | |type="{}"} | ||
| − | $Pr(A_2)$ | + | ${\rm Pr}(A_2) \ = \ ${ 0.1875 3% } |
| − | {Welche Wahrscheinlichkeiten werden sich sehr lange nach Einschalten der Markovkette einstellen $(ν \rightarrow \infty)$? Wie groß ist insbesondere $Pr(A)$? | + | {Welche Wahrscheinlichkeiten werden sich sehr lange nach Einschalten der Markovkette einstellen $(ν \rightarrow \infty)$? <br>Wie groß ist insbesondere die ergodische Wahrscheinlichkeit ${\rm Pr}(A)$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr(A)$ | + | ${\rm Pr}(A) \ = \ $ { 0.333 3% } |
| Zeile 47: | Zeile 58: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Allgemein bzw. in diesem Sonderfall muss gelten: |
| − | '''2 | + | :$$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$ |
| − | '''3 | + | :$$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$ |
| − | '''4 | + | :$$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$ |
| − | + | *Damit lautet die Übergangsmatrix: | |
| − | + | :$${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$ | |
| − | + | ||
| + | |||
| + | |||
| + | '''(2)''' Wegen ${\rm Pr}(B_0) = 1$ und $p_\text{BB} = 0$ kann zum Zeitpunkt $\nu = 1$ das Ereignis $B$ nicht auftreten und $A$ ist sehr viel wahrscheinlicher als $C$: | ||
| + | :$$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$ | ||
| + | *Zum gleichen Ergebnis kommt man durch Anwendung der Vektor-Matrixdarstellung. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Für den Wahrscheinlichkeitsvektor zum Zeitpunkt $\nu = 2$ gilt: | ||
| + | :$${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$ | ||
| + | *Damit ist die Ereigniswahrscheinlichkeit ${\rm Pr}(A_2) = 3/16\hspace{0.15cm}\underline {= 0.1875}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Zur Lösung dieser Aufgabe sollen verschiedene Möglichkeiten angegeben werden. | ||
| + | *Zum einen das Lösen eines Gleichungssystems mit drei Unbekannten: | ||
| + | :$${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$ | ||
| + | :$${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$ | ||
| + | :$${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$ | ||
| + | :Aus der ersten Gleichung erhält man ${\rm Pr}(B) = {\rm Pr}(A)$, aus der letzten ${\rm Pr}(C) = {\rm Pr}(A)$. Da die Summe aller Wahrscheinlichkeiten gleich $1$ ist, folgt $ {\rm Pr}(A) = {\rm Pr}(B) = {\rm Pr}(C) = 1/3 \hspace{0.15cm}\underline {\approx 0.333}$. | ||
| + | *Zum gleichen Ergebnis kommt man durch Analyse der Übergangsmatrix. Da die Summe jeder Spalte gleich $1$ ist $($das heißt: die Summe einer jeden Zeile der transponierten Matrix ergibt ebenfalls $1)$, ist offensichtlich, dass alle Ereigniswahrscheinlichkeiten gleich sein müssen. | ||
| + | |||
| + | *Auch durch kurzes Nachdenken hätte man das Ergebnis ohne Rechnung vorhersagen können. Da bei jedem Ereignis die Zahlenwerte bei den abgehenden Pfeilen (nur zu anderen Ereignissen) mit denen bei den ankommenden gleich sind, ist nicht einzusehen, warum eines der Ereignisse bevorzugt sein sollte. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 12. November 2019, 14:12 Uhr
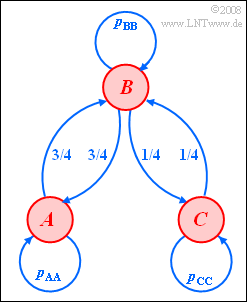
Wir betrachten eine Markovkette mit den drei möglichen Ereignissen $A$, $B$ und $C$:
- Die Übergangswahrscheinlichkeiten sind der Grafik zu entnehmen.
- Ein Übergang von $A$ nach $C$ und umgekehrt ist somit nicht möglich:
- $$p_\text{AC} = p_\text{CA} = 0.$$
Die drei Ereigniswahrscheinlichkeiten zum Startzeitpunkt $\nu = 0$ sind wie folgt gegeben:
- $${\rm Pr}(A_0) = 0,$$
- $${\rm Pr}(B_0) = 1,$$
- $${\rm Pr}(C_0) = 0.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Markovketten.
- Insbesondere wird auf die Seite Matrix-Vektordarstellung Bezug genommen.
Fragebogen
Musterlösung
(1) Allgemein bzw. in diesem Sonderfall muss gelten:
- $$p_{\rm AA} = 1 - p_{\rm AB} - p_{\rm AC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm AA} = 1 - 0.75 -0 \hspace{0.15cm}\underline {= 0.25},$$
- $$p_{\rm BB} = 1 - p_{\rm BA} - p_{\rm BC} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm BB} = 1 - 0.75 -0.25 \hspace{0.15cm}\underline {= 0},$$
- $$p_{\rm CC} = 1 - p_{\rm CA} - p_{\rm CB} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm CC} = 1 - 0 - 0.25 \hspace{0.15cm}\underline {= 0.75}.$$
- Damit lautet die Übergangsmatrix:
- $${\mathbf{P}} = \left[ \begin{array}{ccc} 1/4 & 3/4 & 0 \\ 3/4 & 0 & 1/4 \\ 0 & 1/4 & 3/4 \end{array} \right] .$$
(2) Wegen ${\rm Pr}(B_0) = 1$ und $p_\text{BB} = 0$ kann zum Zeitpunkt $\nu = 1$ das Ereignis $B$ nicht auftreten und $A$ ist sehr viel wahrscheinlicher als $C$:
- $$\hspace{0.15cm}\underline {{\rm Pr}(A_1) = 0.75}; \hspace{0.5cm} {\rm Pr}(B_1) = 0; \hspace{0.5cm}{\rm Pr}(C_1) = 0.25.$$
- Zum gleichen Ergebnis kommt man durch Anwendung der Vektor-Matrixdarstellung.
(3) Für den Wahrscheinlichkeitsvektor zum Zeitpunkt $\nu = 2$ gilt:
- $${\mathbf{p}^{(\nu = 2)}} = {\mathbf{P}}^{\rm T} \cdot {\mathbf{p}^{(\nu =1 )}}= \left[ \begin{array}{ccc} 1/4 & 3/4& 0 \\ 3/4 & 0 & 1/4 \\ 0& 1/4& 3/4 \end{array} \right] \left[ \begin{array}{c} 3/4 \\ 0 \\ 1/4 \end{array} \right] = \left[ \begin{array}{c} 3/16 \\ 10/16 \\ 3/16 \end{array} \right] .$$
- Damit ist die Ereigniswahrscheinlichkeit ${\rm Pr}(A_2) = 3/16\hspace{0.15cm}\underline {= 0.1875}$.
(4) Zur Lösung dieser Aufgabe sollen verschiedene Möglichkeiten angegeben werden.
- Zum einen das Lösen eines Gleichungssystems mit drei Unbekannten:
- $${\rm Pr}(A) = 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B),$$
- $${\rm Pr}(B) = 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{2.8cm} + \hspace{0.1cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C),$$
- $${\rm Pr}(C) = \hspace{2.8cm} 1/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm} 3/4 \hspace{0.05cm} \cdot \hspace{0.05cm} {\rm Pr}(C).$$
- Aus der ersten Gleichung erhält man ${\rm Pr}(B) = {\rm Pr}(A)$, aus der letzten ${\rm Pr}(C) = {\rm Pr}(A)$. Da die Summe aller Wahrscheinlichkeiten gleich $1$ ist, folgt $ {\rm Pr}(A) = {\rm Pr}(B) = {\rm Pr}(C) = 1/3 \hspace{0.15cm}\underline {\approx 0.333}$.
- Zum gleichen Ergebnis kommt man durch Analyse der Übergangsmatrix. Da die Summe jeder Spalte gleich $1$ ist $($das heißt: die Summe einer jeden Zeile der transponierten Matrix ergibt ebenfalls $1)$, ist offensichtlich, dass alle Ereigniswahrscheinlichkeiten gleich sein müssen.
- Auch durch kurzes Nachdenken hätte man das Ergebnis ohne Rechnung vorhersagen können. Da bei jedem Ereignis die Zahlenwerte bei den abgehenden Pfeilen (nur zu anderen Ereignissen) mit denen bei den ankommenden gleich sind, ist nicht einzusehen, warum eines der Ereignisse bevorzugt sein sollte.