Aufgaben:Aufgabe 3.12: Cauchyverteilung: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Weitere Verteilungen }} right| :Die Wahrscheinlichkeitsdichtefunktion s…“) |
|||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
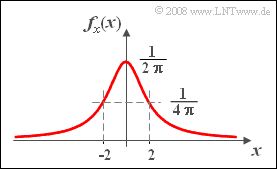
| − | [[Datei:P_ID207__Sto_A_3_12.png|right|]] | + | [[Datei:P_ID207__Sto_A_3_12.png|right|frame|WDF der Cauchyverteilung]] |
| − | + | Die Wahrscheinlichkeitsdichtefunktion der Cauchyverteilung ist wie folgt gegeben: | |
:$$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$ | :$$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$ | ||
| − | + | Aus der Grafik ist bereits der extrem langsame Abfall des WDF–Verlaufs zu erkennen. | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Weitere_Verteilungen|Weitere Verteilungen]]. | ||
| + | *Insbesondere wird auf die Seite [[Stochastische_Signaltheorie/Weitere_Verteilungen#Cauchyverteilung|"Cauchyverteilung"]] Bezug genommen. | ||
| + | |||
| − | |||
| Zeile 15: | Zeile 22: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet die Verteilungsfunktion | + | {Wie lautet die Verteilungsfunktion $F_x(r)$? Mit welcher Wahrscheinlichkeit ist $x$ betragsmäßig kleiner als $2$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr (|x| < 2)$ | + | ${\rm Pr} (|x| < 2) \ = \ $ { 50 3% } $ \ \%$ |
| − | {Mit welcher Wahrscheinlichkeit ist | + | {Mit welcher Wahrscheinlichkeit ist $x$ betragsmäßig größer als $4$? |
|type="{}"} | |type="{}"} | ||
| − | $Pr (|x| > 4)$ | + | ${\rm Pr} (|x| > 4) \ = \ $ { 29.6 3% } $ \ \%$ |
| − | {Welche der | + | {Welche der folgenden Aussagen treffen für die Cauchyverteilung zu? |
|type="[]"} | |type="[]"} | ||
+ Die Cauchyverteilung besitzt eine unendlich große Varianz. | + Die Cauchyverteilung besitzt eine unendlich große Varianz. | ||
| − | + Die Tschebyscheff | + | + Die Tschebyscheff–Ungleichung macht hier keinen Sinn. |
+ Eine in der Natur messbare Zufallsgröße ist nie cauchyverteilt. | + Eine in der Natur messbare Zufallsgröße ist nie cauchyverteilt. | ||
| Zeile 36: | Zeile 43: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Theorieteil, so erkennt man, dass der Parameter $\lambda= 2$ ist. | |
| + | *Daraus folgt (nach Integration über die WDF): | ||
:$$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$ | :$$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$ | ||
| − | + | *Insbesondere sind | |
| − | :$$F_x ( r = 2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$ | + | :$$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$ |
:$$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$ | :$$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$ | ||
| − | + | *Die gesuchte Wahrscheinlichkeit ergibt sich als die Differenz zu | |
| + | :$${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$ | ||
| + | |||
| + | |||
| − | + | '''(2)''' Nach dem Ergebnis der Teilaufgabe '''(1)''' ist $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$. | |
| − | :$${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = | + | *Damit gilt für die „komplementäre” Wahrscheinlichkeit ${\rm Pr} (x > 4)= 0.148$. |
| + | *Die gesuchte Wahrscheinlichkeit ist aus Symmetriegründen doppelt so groß: | ||
| + | :$${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 29.6\%}.$$ | ||
| − | + | ||
| + | |||
| + | '''(3)''' <u>Alle Lösungsvorschläge</u> treffen zu: | ||
| + | *Für die Varianz der Cauchyverteilung gilt nämlich: | ||
:$$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} | :$$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} | ||
\hspace{-0.15cm} | \hspace{-0.15cm} | ||
\frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$ | \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$ | ||
| − | + | *Für große $x$ liefert der Integrand den konstanten Wert $4$. Deshalb divergiert das Integral. | |
| − | + | *Mit $\sigma_x \to \infty$ liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke. | |
| − | + | *„Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten. | |
| − | „Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten. Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße | + | *Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße nicht dieser Beschränkung. Beispiel: Der Quotient zweier mittelwertfreier Gaußgrößen. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 3. Februar 2022, 13:30 Uhr
Die Wahrscheinlichkeitsdichtefunktion der Cauchyverteilung ist wie folgt gegeben:
- $$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$
Aus der Grafik ist bereits der extrem langsame Abfall des WDF–Verlaufs zu erkennen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
- Insbesondere wird auf die Seite "Cauchyverteilung" Bezug genommen.
Fragebogen
Musterlösung
(1) Vergleicht man die vorgegebene WDF mit der allgemeinen Gleichung im Theorieteil, so erkennt man, dass der Parameter $\lambda= 2$ ist.
- Daraus folgt (nach Integration über die WDF):
- $$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$
- Insbesondere sind
- $$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$
- $$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$
- Die gesuchte Wahrscheinlichkeit ergibt sich als die Differenz zu
- $${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$
(2) Nach dem Ergebnis der Teilaufgabe (1) ist $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$.
- Damit gilt für die „komplementäre” Wahrscheinlichkeit ${\rm Pr} (x > 4)= 0.148$.
- Die gesuchte Wahrscheinlichkeit ist aus Symmetriegründen doppelt so groß:
- $${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 29.6\%}.$$
(3) Alle Lösungsvorschläge treffen zu:
- Für die Varianz der Cauchyverteilung gilt nämlich:
- $$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \hspace{-0.15cm} \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$
- Für große $x$ liefert der Integrand den konstanten Wert $4$. Deshalb divergiert das Integral.
- Mit $\sigma_x \to \infty$ liefert aber auch die Tschebyscheffsche Ungleichung keine auswertbare Schranke.
- „Natürliche“ Zufallsgrößen (physikalisch interpretierbar) können nie cauchyverteilt sein, da sie sonst eine unendlich große Leistung besitzen müssten.
- Dagegen unterliegt eine „künstliche“ (oder mathematische) Zufallsgröße nicht dieser Beschränkung. Beispiel: Der Quotient zweier mittelwertfreier Gaußgrößen.