Aufgaben:Aufgabe 4.7Z: Erzeugung einer 2D–WDF: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Stochastische Signaltheorie/Linearkombinationen von Zufallsgrößen }} right| :Ausgehend von statist…“) |
|||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID423__Sto_Z_4_7.png|right|]] | + | [[Datei:P_ID423__Sto_Z_4_7.png|right|frame|Vorgaben zur Erzeugung einer <br>2D-Zufallsgröße]] |
| − | + | Ausgehend von statistisch unabhängigen Größen $u$ und $v$, | |
| + | *die beide zwischen $-1$ und $+1$ gleichverteilt sind und | ||
| + | *somit jeweils die Varianz $\sigma^2 = 2/3$ besitzen, | ||
| + | |||
| + | |||
| + | soll eine 2D-Zufallsgröße $(x,\hspace{0.08cm} y)$ generiert werden, wobei für die Komponenten gilt: | ||
:$$x = A \cdot u + B \cdot v + C,$$ | :$$x = A \cdot u + B \cdot v + C,$$ | ||
:$$y= D \cdot u + E \cdot v + F.$$ | :$$y= D \cdot u + E \cdot v + F.$$ | ||
| − | + | Die zu erzeugende 2D–Zufallsgröße $(x,\hspace{0.08cm} y)$ soll die folgenden statistischen Eigenschaften aufweisen: | |
| + | * Die Varianzen seien $\sigma_x^2 = 4$ und $\sigma_y^2 = 10$. | ||
| + | * Die Zufallsgröße $x$ sei mittelwertfrei $(m_x =0)$. | ||
| + | * Für den Mittelwert von $y$ gelte $m_y = 1$. | ||
| + | * Der Korrelationskoeffizient zwischen $x$ und $y$ betrage $\rho_{xy} = \sqrt{0.9} = 0.949.$ | ||
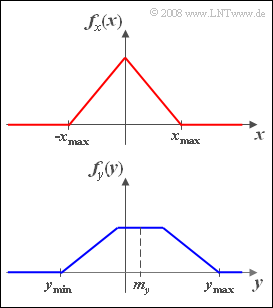
| + | * Die Zufallsgröße $x$ besitze eine dreieckförmige WDF $f_x(x)$ entsprechend der oberen Skizze. | ||
| + | * Die Zufallsgröße $y$ besitze eine trapezförmige WDF $f_y(y)$ entsprechend der unteren Skizze. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | :* Die | + | Hinweise: |
| − | + | *Die Aufgabe gehört zum Kapitel [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen|Linearkombinationen von Zufallsgrößen]]. | |
| − | + | *Insbesondere wird Bezug genommen auf die Seite [[Stochastische_Signaltheorie/Linearkombinationen_von_Zufallsgrößen#Erzeugung_korrelierter_Zufallsgr.C3.B6.C3.9Fen|Erzeugung korrelierter Zufallsgrößen]]. | |
| − | + | *Um Mehrdeutigkeiten zu vermeiden wird festgelegt, dass alle Koeffizienten $A$, ... , $F$ nicht negativ sein sollen. | |
| − | + | ||
| Zeile 29: | Zeile 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bestimmen Sie die Koeffizienten | + | {Bestimmen Sie die Koeffizienten $C$ und $F$. |
|type="{}"} | |type="{}"} | ||
| − | $C$ | + | $C \ = \ $ { 0. } |
| − | $F$ | + | $F\ = \ $ { 1 3% } |
| − | {Bestimmen Sie die Koeffizienten | + | {Bestimmen Sie die Koeffizienten $A$ und $B$. |
|type="{}"} | |type="{}"} | ||
| − | $A$ | + | $A \ = \ $ { 1.732 3% } |
| − | $B$ | + | $B \ = \ $ { 1.732 3% } |
| − | {Bestimmen Sie die Koeffizienten | + | {Bestimmen Sie die Koeffizienten $D$ und $E$, wobei $D > E$ gelten soll. |
|type="{}"} | |type="{}"} | ||
| − | $D$ | + | $D \ = \ $ { 3.464 3% } |
| − | $E$ | + | $E \ = \ $ { 1.732 3% } |
| − | {Geben Sie die Maximalwerte für | + | {Geben Sie die Maximalwerte für $x$ und $y$ an. |
|type="{}"} | |type="{}"} | ||
| − | $x_\text{max}$ | + | $x_\text{max}\ = \ $ { 3.464 3% } |
| − | $y_\text{max}$ | + | $y_\text{max}\ = \ $ { 6.196 3% } |
| Zeile 57: | Zeile 63: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Aufgrund der angegebenen Mittelwerte muss gelten: | |
| + | :$$ C = m_x\hspace{0.15cm}\underline{ = 0},$$ | ||
| + | :$$ F = m_y\hspace{0.15cm}\underline{ = 1}.$$ | ||
| + | |||
| − | + | '''(2)''' Unter Berücksichtigung von $\sigma^2 = 2/3$ gilt: | |
| − | :$$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= | + | :$$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= {2}/{3} \cdot ( A^2 + B^2) .$$ |
| − | + | *Wegen $\sigma_x^2 = 4$ folgt $A^2 + B^2= 6$. | |
| + | *Eine dreieckförmige WDF bedeutet, dass $A = \pm B$ gelten muss. | ||
| + | *Somit erhält man, da negative Koeffizienten ausgeschlossen wurden: | ||
| + | :$$ A = B = \sqrt{3}\hspace{0.15cm}\underline{ = 1.732}.$$ | ||
| − | : | + | |
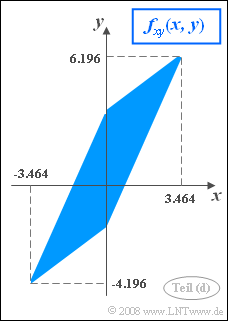
| + | [[Datei:P_ID424__Sto_Z_4_7_d.png|right|frame|Rautenförmige 2D-WDF]] | ||
| + | '''(3)''' Mit $ A = B = \sqrt{3}$ entsprechend der letzten Teilaufgabe verbleiben zwei Bestimmungsgleichungen für $D$ und $E$: | ||
:$$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$ | :$$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$ | ||
:$$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$ | :$$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$ | ||
| − | |||
| − | + | *Daraus folgt weiter: $D + E = \sqrt{1.8 \cdot ( D^2 + E^2)} = \sqrt{27} = 3 \cdot \sqrt{3}.$ | |
| − | + | *Die Gleichung führt in Verbindung mit $D^2 + E^2 = 15$ und der Nebenbedingung $(D>E)$ zum Ergebnis: | |
| + | :$$ D= 2 \cdot \sqrt{3}\hspace{0.15cm}\underline{ = 3.464}, \hspace{0.5cm}E= \sqrt{3} \hspace{0.15cm}\underline{= 1.732}.$$ | ||
| − | |||
| − | |||
| − | + | '''(4)''' Die Zufallsgröße $x$ bzw. $y$ nehmen ihre maximalen Werte an, wenn jeweils $u= +1$ und $v= +1$ gilt: | |
| + | :$$ x_\text{max}= A+B \hspace{0.15cm}\underline{ = +3.464}, \hspace{0.5cm} x_\text{min} = - A - B= -3.464.$$ | ||
| + | :$$ y_\text{max}= D+E+F \hspace{0.15cm}\underline{ = +6.196}, \hspace{0.5cm} y_\text{min} = -D-E+F= -4.196.$$ | ||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Stochastische Signaltheorie|^4.3 Linearkombinationen | + | [[Category:Aufgaben zu Stochastische Signaltheorie|^4.3 Linearkombinationen^]] |
Aktuelle Version vom 25. Februar 2022, 18:01 Uhr
Ausgehend von statistisch unabhängigen Größen $u$ und $v$,
- die beide zwischen $-1$ und $+1$ gleichverteilt sind und
- somit jeweils die Varianz $\sigma^2 = 2/3$ besitzen,
soll eine 2D-Zufallsgröße $(x,\hspace{0.08cm} y)$ generiert werden, wobei für die Komponenten gilt:
- $$x = A \cdot u + B \cdot v + C,$$
- $$y= D \cdot u + E \cdot v + F.$$
Die zu erzeugende 2D–Zufallsgröße $(x,\hspace{0.08cm} y)$ soll die folgenden statistischen Eigenschaften aufweisen:
- Die Varianzen seien $\sigma_x^2 = 4$ und $\sigma_y^2 = 10$.
- Die Zufallsgröße $x$ sei mittelwertfrei $(m_x =0)$.
- Für den Mittelwert von $y$ gelte $m_y = 1$.
- Der Korrelationskoeffizient zwischen $x$ und $y$ betrage $\rho_{xy} = \sqrt{0.9} = 0.949.$
- Die Zufallsgröße $x$ besitze eine dreieckförmige WDF $f_x(x)$ entsprechend der oberen Skizze.
- Die Zufallsgröße $y$ besitze eine trapezförmige WDF $f_y(y)$ entsprechend der unteren Skizze.
Hinweise:
- Die Aufgabe gehört zum Kapitel Linearkombinationen von Zufallsgrößen.
- Insbesondere wird Bezug genommen auf die Seite Erzeugung korrelierter Zufallsgrößen.
- Um Mehrdeutigkeiten zu vermeiden wird festgelegt, dass alle Koeffizienten $A$, ... , $F$ nicht negativ sein sollen.
Fragebogen
Musterlösung
(1) Aufgrund der angegebenen Mittelwerte muss gelten:
- $$ C = m_x\hspace{0.15cm}\underline{ = 0},$$
- $$ F = m_y\hspace{0.15cm}\underline{ = 1}.$$
(2) Unter Berücksichtigung von $\sigma^2 = 2/3$ gilt:
- $$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= {2}/{3} \cdot ( A^2 + B^2) .$$
- Wegen $\sigma_x^2 = 4$ folgt $A^2 + B^2= 6$.
- Eine dreieckförmige WDF bedeutet, dass $A = \pm B$ gelten muss.
- Somit erhält man, da negative Koeffizienten ausgeschlossen wurden:
- $$ A = B = \sqrt{3}\hspace{0.15cm}\underline{ = 1.732}.$$
(3) Mit $ A = B = \sqrt{3}$ entsprechend der letzten Teilaufgabe verbleiben zwei Bestimmungsgleichungen für $D$ und $E$:
- $$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$
- $$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$
- Daraus folgt weiter: $D + E = \sqrt{1.8 \cdot ( D^2 + E^2)} = \sqrt{27} = 3 \cdot \sqrt{3}.$
- Die Gleichung führt in Verbindung mit $D^2 + E^2 = 15$ und der Nebenbedingung $(D>E)$ zum Ergebnis:
- $$ D= 2 \cdot \sqrt{3}\hspace{0.15cm}\underline{ = 3.464}, \hspace{0.5cm}E= \sqrt{3} \hspace{0.15cm}\underline{= 1.732}.$$
(4) Die Zufallsgröße $x$ bzw. $y$ nehmen ihre maximalen Werte an, wenn jeweils $u= +1$ und $v= +1$ gilt:
- $$ x_\text{max}= A+B \hspace{0.15cm}\underline{ = +3.464}, \hspace{0.5cm} x_\text{min} = - A - B= -3.464.$$
- $$ y_\text{max}= D+E+F \hspace{0.15cm}\underline{ = +6.196}, \hspace{0.5cm} y_\text{min} = -D-E+F= -4.196.$$