Aufgaben:Aufgabe 2.1Z: Verzerrung und Entzerrung: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Klassifizierung der Verzerrungen }} right| :Die Grafik zeigt drei kon…“) |
|||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID880__LZI_Z_2_1.png|right|]] | + | [[Datei:P_ID880__LZI_Z_2_1.png|right|frame|Drei kontinuierliche Spektralfunktionen]] |
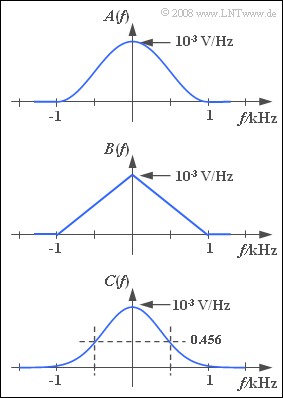
| − | + | Die Grafik zeigt drei kontinuierliche Spektralfunktionen: | |
| − | + | * ein cos<sup>2</sup>–Spektrum, das nur Anteile im Bereich $|f| < 1 \ \rm kHz$ besitzt, wobei gilt: | |
| − | :$$A(f) = 10^{\rm -3} \ | + | :$$A(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \cos^2(\frac{|f|}{1 \, \rm kHz} \cdot \frac{\pi}{ 2} ) ,$$ |
| − | |||
| − | + | * ein Dreieckspektrum, ebenfalls begrenzt auf den Frequenzbereich $|f| < 1 \ \rm kHz$: | |
| − | :$$B(f) = 10^{\rm -3} \ | + | :$$B(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \left(1-\frac{|f|}{1 \, \rm kHz} \right),$$ |
| − | |||
| − | + | * ein so genanntes Gaußspektrum: | |
| − | :$$C(f) = 10^{\rm -3} \ | + | :$$C(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot {\rm e}^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} (f/{1 \, \rm kHz})^2} .$$ |
| − | |||
| − | + | Weiterhin betrachten wir | |
| + | *ein linear verzerrendes System $S_{\rm V}$ mit $X(f)$ am Eingang und $Y(f)$ am Ausgang, sowie | ||
| + | *das Entzerrungssystem $S_{\rm E}$ mit Eingangsspektrum $Y(f)$ und Ausgangsspektrum $Z(f)$. | ||
| − | |||
| − | + | Die Frequenzgänge der beiden Systeme $S_{\rm V}$ und $S_{\rm E}$ lauten: | |
| − | :$$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$ | + | :$$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}$$ |
| + | :$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Lineare_zeitinvariante_Systeme/Klassifizierung_der_Verzerrungen|Klassifizierung der Verzerrungen]]. | ||
| + | *Eine vollständige Entzerrung bedeutet, dass $Z(f) = X(f)$ gilt. | ||
| − | |||
| Zeile 32: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Ist mit einem linearen System die Konstellation | + | {Ist mit einem linearen System die Konstellation $X(f) = A(f)$ und $Y(f) = B(f)$ möglich? Begründen Sie Ihre Antwort. |
| − | |type=" | + | |type="()"} |
+ Ja. | + Ja. | ||
- Nein. | - Nein. | ||
| − | {Es gelte weiterhin | + | {Es gelte weiterhin $X(f) = A(f)$ und $Y(f) = B(f)$. Ist mit einem linearen Filter $H_{\rm E}(f)$ eine vollständige Entzerrung möglich? <br>Wenn JA, so geben Sie bitte $H_{\rm E}(f)$ an. |
| − | |type=" | + | |type="()"} |
+ Ja. | + Ja. | ||
- Nein. | - Nein. | ||
| − | {Ist mit einem linearen System die Konstellation | + | {Ist mit einem linearen System die Konstellation $X(f) = C(f)$ und $Y(f) = B(f)$ möglich? Begründen Sie Ihre Antwort. |
| − | |type=" | + | |type="()"} |
+ Ja. | + Ja. | ||
- Nein. | - Nein. | ||
| − | {Es gelte weiterhin | + | {Es gelte weiterhin $X(f) = C(f)$ und $Y(f) = B(f)$. Ist mit einem linearen Filter $H_{\rm E}(f)$ eine vollständige Entzerrung möglich? <br>Wenn JA, so geben Sie bitte $H_{\rm E}(f)$ an. |
| − | |type=" | + | |type="()"} |
- Ja. | - Ja. | ||
+ Nein. | + Nein. | ||
| − | {Ist mit einem linearen System die Konstellation | + | {Ist mit einem linearen System die Konstellation $X(f) = A(f)$ und $Y(f) = C(f)$ möglich? <br>Begründen Sie Ihre Antwort. |
| − | |type=" | + | |type="()"} |
- Ja. | - Ja. | ||
+ Nein. | + Nein. | ||
| − | |||
| − | |||
</quiz> | </quiz> | ||
| Zeile 67: | Zeile 72: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Richtig ist <u>Ja</u>: | |
| + | *Diese Konstellation ist möglich, da für alle $Y(f) \ne 0$ auch $X(f)$ stets von Null verschieden ist. | ||
| + | *Für alle Frequenzen kleiner als $0.5 \ \rm kHz$ bewirkt $H_{\rm V} = B(f)/A(f) < 1$ eine Dämpfung. | ||
| + | * Die Frequenzen zwischen $0.5 \ \rm kHz$ und $1 \ \rm kHz$ werden dagegen durch das System angehoben. | ||
| − | + | ||
| + | |||
| + | '''(2)''' Richtig ist <u>Ja</u>: | ||
| + | *Bei dieser Konstellation ist auch eine vollständige lineare Entzerrung mit | ||
:$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$ | :$$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$ | ||
| − | :möglich, da beide Spektren genau bis 1 kHz | + | :möglich, da beide Spektren genau bis $1 \ \rm kHz$ reichen. |
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig ist <u>Ja</u>: | ||
| + | *Auch diese Konstellation ist möglich. Das Filter $H_{\rm V}(f)$ muss für die Frequenzen $|f| <1 \ \rm kHz$ aus dem Gaußspektrum ein Dreieckspektrum formen und alle Frequenzen $|f| > 1 \ \rm kHz$ unterdrücken. | ||
| + | |||
| + | |||
| − | + | '''(4)''' Richtig ist <u>Nein</u>: | |
| + | *Eine vollständige Entzerrung ist hier nicht möglich: | ||
| + | *Die Anteile des Gaußspektrums, die durch $H_{\rm V}(f)$ vollständig eliminiert wurden, können durch das lineare System nicht wieder hergestellt werden. | ||
| − | |||
| − | |||
| − | :Die Frage, ob es ein nichtlineares System gibt, das aus dem cos | + | '''(5)''' Richtig ist <u>Nein</u>: |
| + | *Diese Konstellation ist mit einem linearen System nicht möglich, da im Spektrum $C(f) = A(f) \cdot H_{\rm V}(f)$ keine Spektralanteile enthalten sein können, die es in $A(f)$ nicht gibt. | ||
| + | *Die Frage, ob es ein nichtlineares System gibt, das aus dem $\cos^2$-Spektrum ein Gaußspektrum formt, ist nicht gestellt und muss deshalb auch nicht beantwortet werden: Die Autoren glauben eher „Nein”. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 28. Oktober 2019, 09:05 Uhr
Die Grafik zeigt drei kontinuierliche Spektralfunktionen:
- ein cos2–Spektrum, das nur Anteile im Bereich $|f| < 1 \ \rm kHz$ besitzt, wobei gilt:
- $$A(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \cos^2(\frac{|f|}{1 \, \rm kHz} \cdot \frac{\pi}{ 2} ) ,$$
- ein Dreieckspektrum, ebenfalls begrenzt auf den Frequenzbereich $|f| < 1 \ \rm kHz$:
- $$B(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot \left(1-\frac{|f|}{1 \, \rm kHz} \right),$$
- ein so genanntes Gaußspektrum:
- $$C(f) = 10^{\rm -3} \ {\rm V}/{\rm Hz} \cdot {\rm e}^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} (f/{1 \, \rm kHz})^2} .$$
Weiterhin betrachten wir
- ein linear verzerrendes System $S_{\rm V}$ mit $X(f)$ am Eingang und $Y(f)$ am Ausgang, sowie
- das Entzerrungssystem $S_{\rm E}$ mit Eingangsspektrum $Y(f)$ und Ausgangsspektrum $Z(f)$.
Die Frequenzgänge der beiden Systeme $S_{\rm V}$ und $S_{\rm E}$ lauten:
- $$H_{\rm V}(f) = \frac{Y(f)}{X(f)} , \hspace{0.3cm}$$
- $$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} .$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Klassifizierung der Verzerrungen.
- Eine vollständige Entzerrung bedeutet, dass $Z(f) = X(f)$ gilt.
Fragebogen
Musterlösung
(1) Richtig ist Ja:
- Diese Konstellation ist möglich, da für alle $Y(f) \ne 0$ auch $X(f)$ stets von Null verschieden ist.
- Für alle Frequenzen kleiner als $0.5 \ \rm kHz$ bewirkt $H_{\rm V} = B(f)/A(f) < 1$ eine Dämpfung.
- Die Frequenzen zwischen $0.5 \ \rm kHz$ und $1 \ \rm kHz$ werden dagegen durch das System angehoben.
(2) Richtig ist Ja:
- Bei dieser Konstellation ist auch eine vollständige lineare Entzerrung mit
- $$H_{\rm E}(f) = \frac{Z(f)}{Y(f)} = \frac{A(f)}{B(f)} = \frac{1}{H_{\rm V}(f)}$$
- möglich, da beide Spektren genau bis $1 \ \rm kHz$ reichen.
(3) Richtig ist Ja:
- Auch diese Konstellation ist möglich. Das Filter $H_{\rm V}(f)$ muss für die Frequenzen $|f| <1 \ \rm kHz$ aus dem Gaußspektrum ein Dreieckspektrum formen und alle Frequenzen $|f| > 1 \ \rm kHz$ unterdrücken.
(4) Richtig ist Nein:
- Eine vollständige Entzerrung ist hier nicht möglich:
- Die Anteile des Gaußspektrums, die durch $H_{\rm V}(f)$ vollständig eliminiert wurden, können durch das lineare System nicht wieder hergestellt werden.
(5) Richtig ist Nein:
- Diese Konstellation ist mit einem linearen System nicht möglich, da im Spektrum $C(f) = A(f) \cdot H_{\rm V}(f)$ keine Spektralanteile enthalten sein können, die es in $A(f)$ nicht gibt.
- Die Frage, ob es ein nichtlineares System gibt, das aus dem $\cos^2$-Spektrum ein Gaußspektrum formt, ist nicht gestellt und muss deshalb auch nicht beantwortet werden: Die Autoren glauben eher „Nein”.