Aufgaben:Aufgabe 1.2Z: Pulscodemodulation: Unterschied zwischen den Versionen
Aus LNTwww
Nabil (Diskussion | Beiträge) |
|||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{quiz-Header|Buchseite=Signaldarstellung/Prinzip der Nachrichtenübertragung}} | {{quiz-Header|Buchseite=Signaldarstellung/Prinzip der Nachrichtenübertragung}} | ||
| − | |||
| − | |||
| − | |||
| − | + | [[Datei:P_ID342__Sig_Z_1_2.png|right|frame|Komponenten der Pulscodemodulation]] | |
| + | Alle modernen Nachrichtenübertragungssysteme sind digital. Das Prinzip der digitalen Übertragung von Sprachsignalen geht auf [https://de.wikipedia.org/wiki/Alec_Reeves Alec Reeves] zurück, der die so genannte ''Pulscodemodulation'' $\rm (PCM)$ bereits 1938 erfunden hat. | ||
| − | :* Das bandbegrenzte Sprachsignal $ | + | Rechts sehen Sie das (vereinfachte) Blockschaltbild des PCM–Senders mit drei Funktionseinheiten: |
| + | * Das bandbegrenzte Sprachsignal ${q(t)}$ wird abgetastet, wobei das [[Signaldarstellung/Zeitdiskrete_Signaldarstellung#Das_Abtasttheorem|Abtasttheorem]] zu beachten ist, und ergibt das abgetastete Signal $q_{\rm A}(t)$. | ||
| + | * Jeder Abtastwert $q_{\rm A}(t)$ wird auf einen von $M = 2^N$ quantisierten Werten abgebildet und führt zum quantisierten Signal $q_{\rm Q}(t)$. | ||
| + | * Jeder einzelne Quantisierungswert wird durch eine Codefolge von $N$ Binärsymbolen dargestellt und ergibt das codierte Signal $q_{\rm C}(t)$. | ||
| − | |||
| − | : | + | In dieser Aufgabe sollen nur die verschiedenen Signale des PCM–Senders klassifiziert werden. Spätere Aufgaben behandeln weitere Eigenschaften der Pulscodemodulation. |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweis:'' Die Aufgabe gehört zum Kapitel [[Signaldarstellung/Klassifizierung_von_Signalen|Klassifizierung von Signalen]]. | ||
| − | |||
| − | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Welche der Aussagen sind für das Quellensignal $ | + | {Welche der Aussagen sind für das Quellensignal ${q(t)}$ zutreffend? |
|type="[]"} | |type="[]"} | ||
| − | + Im Normalbetrieb ist $ | + | + Im Normalbetrieb ist ${q(t)}$ ein stochastisches Signal. |
+ Ein deterministisches Quellensignal ist nur bei Testbetrieb oder für theoretische Untersuchungen sinnvoll. | + Ein deterministisches Quellensignal ist nur bei Testbetrieb oder für theoretische Untersuchungen sinnvoll. | ||
| − | - $ | + | - ${q(t)}$ ist ein zeitdiskretes Signal. |
| − | + | + ${q(t)}$ ist ein wertkontinuierliches Signal. | |
| − | {Welche der Aussagen treffen für das abgetastete Signal $ | + | {Welche der Aussagen treffen für das abgetastete Signal $q_{\rm A}(t)$ zu? |
|type="[]"} | |type="[]"} | ||
| − | - $ | + | - $q_{\rm A}(t)$ ist ein wertdiskretes Signal. |
| − | + $ | + | + $q_{\rm A}(t)$ ist ein zeitdiskretes Signal. |
+ Je größer die maximale Frequenz des Nachrichtensignals ist, desto größer muss die Abtastrate gewählt werden. | + Je größer die maximale Frequenz des Nachrichtensignals ist, desto größer muss die Abtastrate gewählt werden. | ||
| − | {Welche Aussagen sind für das quantisierte Signal $ | + | {Welche Aussagen sind für das quantisierte Signal $q_{\rm Q}(t)$ zutreffend, wenn $N = 8$ zugrunde gelegt wird? |
|type="[]"} | |type="[]"} | ||
| − | + $ | + | + $q_{\rm Q}(t)$ ist ein zeitdiskretes Signal. |
| − | - $ | + | - $q_{\rm Q}(t)$ ist wertdiskret mit $M = 8$ möglichen Werten. |
| − | + $ | + | + $q_{\rm Q}(t)$ ist wertdiskret mit $M = 256$ möglichen Werten. |
| − | - $ | + | - $q_{\rm Q}(t)$ ist ein Binärsignal. |
| − | {Welche Aussagen sind für das codierte Signal $ | + | {Welche Aussagen sind für das codierte Signal $q_{\rm C}(t)$ zutreffend, wenn $N = 8$ zugrunde gelegt wird? |
|type="[]"} | |type="[]"} | ||
| − | + $ | + | + $q_{\rm C}(t)$ ist ein zeitdiskretes Signal. |
| − | - $ | + | - $q_{\rm C}(t)$ ist ein wertdiskretes Signal mit $M = 8$ möglichen Werten. |
| − | + $ | + | + $q_{\rm C}(t)$ ist ein Binärsignal. |
| − | - Bei Abtastung im Abstand $ | + | - Bei Abtastung im Abstand $T_{\rm A}$ beträgt die Bitdauer $T_{\rm B} = T_{\rm A}$. |
| − | + Bei Abtastung im Abstand $ | + | + Bei Abtastung im Abstand $T_{\rm A}$ beträgt die Bitdauer $T_{\rm B} = T_{\rm A}/8$. |
| Zeile 57: | Zeile 62: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig sind die <u>Lösungsvorschläge 1, 2 und 4</u>: |
| + | *Das Quellensignal ${q(t)}$ ist analog, also wert- und zeitkontinuierlich. | ||
| + | *Im Allgemeinen macht es keinen Sinn, ein deterministisches Signal zu übertragen. | ||
| + | *Für die mathematische Beschreibung eignet sich ein deterministisches Quellensignal – wie zum Beispiel ein periodisches Signal – besser als ein Zufallssignal. | ||
| + | *Deterministische Signale werden auch für den Testbetrieb herangezogen, um erkannte Fehlfunktionen rekonstruieren zu können. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Richtig sind die <u>Lösungsvorschläge 2 und 3</u>: | ||
| + | *Das Signal $q_{\rm A}(t)$ nach der Abtastung ist weiterhin wertkontinuierlich , aber nun zeitdiskret. | ||
| + | *Die Abtastfrequenz $f_{\rm A}$ ist dabei durch das so genannte Abtasttheorem vorgegeben. | ||
| + | *Je größer die maximale Frequenz $f_{\rm N,\,max}$ des Nachrichtensignals ist, desto größer muss $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ gewählt werden. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
| + | *Das quantisierte Signal $q_{\rm Q}(t)$ ist zeit- und wertdiskret, wobei die Stufenzahl $M = 2^8 = 256$ beträgt. | ||
| + | *Ein Binärsignal ist dagegen ein wertdiskretes Signal mit der Stufenzahl $M = 2$. | ||
| + | |||
| − | |||
| − | |||
| − | '''4 | + | '''(4)''' Richtig sind die <u>Lösungsvorschläge 1, 3 und 5</u>: |
| + | *Das codierte Signal $q_{\rm C}(t)$ ist binär $($Stufenzahl $M = 2)$ mit Bitdauer $T_{\rm B} = T_{\rm A}/8$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 9. April 2021, 13:14 Uhr
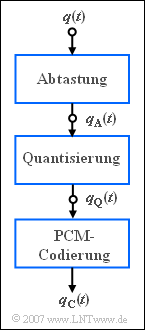
Alle modernen Nachrichtenübertragungssysteme sind digital. Das Prinzip der digitalen Übertragung von Sprachsignalen geht auf Alec Reeves zurück, der die so genannte Pulscodemodulation $\rm (PCM)$ bereits 1938 erfunden hat.
Rechts sehen Sie das (vereinfachte) Blockschaltbild des PCM–Senders mit drei Funktionseinheiten:
- Das bandbegrenzte Sprachsignal ${q(t)}$ wird abgetastet, wobei das Abtasttheorem zu beachten ist, und ergibt das abgetastete Signal $q_{\rm A}(t)$.
- Jeder Abtastwert $q_{\rm A}(t)$ wird auf einen von $M = 2^N$ quantisierten Werten abgebildet und führt zum quantisierten Signal $q_{\rm Q}(t)$.
- Jeder einzelne Quantisierungswert wird durch eine Codefolge von $N$ Binärsymbolen dargestellt und ergibt das codierte Signal $q_{\rm C}(t)$.
In dieser Aufgabe sollen nur die verschiedenen Signale des PCM–Senders klassifiziert werden. Spätere Aufgaben behandeln weitere Eigenschaften der Pulscodemodulation.
Hinweis: Die Aufgabe gehört zum Kapitel Klassifizierung von Signalen.
Fragebogen
Musterlösung
(1) Richtig sind die Lösungsvorschläge 1, 2 und 4:
- Das Quellensignal ${q(t)}$ ist analog, also wert- und zeitkontinuierlich.
- Im Allgemeinen macht es keinen Sinn, ein deterministisches Signal zu übertragen.
- Für die mathematische Beschreibung eignet sich ein deterministisches Quellensignal – wie zum Beispiel ein periodisches Signal – besser als ein Zufallssignal.
- Deterministische Signale werden auch für den Testbetrieb herangezogen, um erkannte Fehlfunktionen rekonstruieren zu können.
(2) Richtig sind die Lösungsvorschläge 2 und 3:
- Das Signal $q_{\rm A}(t)$ nach der Abtastung ist weiterhin wertkontinuierlich , aber nun zeitdiskret.
- Die Abtastfrequenz $f_{\rm A}$ ist dabei durch das so genannte Abtasttheorem vorgegeben.
- Je größer die maximale Frequenz $f_{\rm N,\,max}$ des Nachrichtensignals ist, desto größer muss $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ gewählt werden.
(3) Richtig sind die Lösungsvorschläge 1 und 3:
- Das quantisierte Signal $q_{\rm Q}(t)$ ist zeit- und wertdiskret, wobei die Stufenzahl $M = 2^8 = 256$ beträgt.
- Ein Binärsignal ist dagegen ein wertdiskretes Signal mit der Stufenzahl $M = 2$.
(4) Richtig sind die Lösungsvorschläge 1, 3 und 5:
- Das codierte Signal $q_{\rm C}(t)$ ist binär $($Stufenzahl $M = 2)$ mit Bitdauer $T_{\rm B} = T_{\rm A}/8$.