Aufgaben:Aufgabe 2.2Z: Mittlere Codewortlänge: Unterschied zwischen den Versionen
Nabil (Diskussion | Beiträge) K (Nabil verschob die Seite Zusatzaufgaben:2.02 Mittlere Codewortlänge nach 2.02Z Mittlere Codewortlänge) |
|||
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Informationstheorie | + | {{quiz-Header|Buchseite=Informationstheorie/Allgemeine Beschreibung |
}} | }} | ||
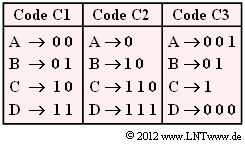
| − | [[Datei:P_ID2417__Inf_Z_2_2.png|right|]] | + | [[Datei:P_ID2417__Inf_Z_2_2.png|right|frame|Tabelle zur Quellencodierung]] |
| − | + | Ziel von Datenkomprimierung ist es, die Nachricht einer Quelle mit möglichst wenigen Binärzeichen darzustellen. | |
| − | + | Wir betrachten hier eine wertdiskrete Nachrichtenquelle mit dem Symbolvorrat $\rm \{ A, \ B, \ C, \ D\}$ ⇒ Symbolumfang $M = 4$ und den Auftrittswahrscheinlichkeiten | |
| + | :*$p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ (Teilaufgabe 1), | ||
| + | :* $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ (ab Teilaufgabe 2). | ||
| − | |||
| − | + | Vorausgesetzt wird, dass es zwischen den einzelnen Quellensymbolen keine statistischen Bindungen gibt. | |
| − | + | Ein Maß für die Güte eines Komprimierungsverfahrens ist die mittlere Codewortlänge $L_{\rm M}$ mit der Zusatzeinheit „bit/Quellensymbol”. | |
| − | : | + | Vorgegeben sind drei Zuordnungen. Anzumerken ist: |
| + | * Jeder dieser Binärcodes $\rm C1$, $\rm C2$ und $\rm C3$ ist für eine spezielle Quellenstatistik ausgelegt. | ||
| + | * Alle Codes sind präfixfrei und somit ohne weitere Angabe sofort decodierbar. | ||
| − | |||
| − | |||
| − | + | ||
| + | |||
| + | ''Hinweis:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Allgemeine_Beschreibung|Allgemeine Beschreibung der Quellencodierung]]. | ||
| + | |||
| Zeile 26: | Zeile 31: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Bestimmen Sie die mittlere Codewortlänge für | + | {Bestimmen Sie die mittlere Codewortlänge $L_{\rm M}$ für $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$. |
|type="{}"} | |type="{}"} | ||
| − | $C1:\ \ | + | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/Quellensymbol$ |
| − | $C2:\ | + | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/Quellensymbol$ |
| − | $C3:\ | + | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.25 1% } $\ \rm bit/Quellensymbol$ |
| − | {Welche Werte ergeben sich für | + | {Welche Werte ergeben sich für $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$? |
|type="{}"} | |type="{}"} | ||
| − | $C1:\ | + | $\text{C1:}\ \ L_{\rm M} \ = \ $ { 2 1% } $\ \rm bit/Quellensymbol$ |
| − | $C2:\ | + | $\text{C2:}\ \ L_{\rm M} \ = \ $ { 1.75 1% } $\ \rm bit/Quellensymbol$ |
| − | $C3:\ | + | $\text{C3:}\ \ L_{\rm M} \ = \ $ { 2.5 1% } $\ \rm bit/Quellensymbol$ |
| Zeile 46: | Zeile 51: | ||
| − | {Für die spezielle | + | {Für die spezielle Quellensymbolfolge $\rm ADBDCBCBADCA$ ergibt sich die Codesymbolfolge $\rm 001101111001100100111000$. |
| − | |type=" | + | <br>Welcher Code wurde verwendet? |
| − | + | + | |type="()"} |
| − | - der Code C2. | + | + Der Code $\rm C1$, |
| + | - der Code $\rm C2$. | ||
| − | {Nach Codierung mit C3 erhält man | + | {Nach Codierung mit $\rm C3$ erhält man $\rm 001101111001100100111000$. Wie lautet die zugehörige Quellensymbolfolge? |
| − | |type=" | + | |type="()"} |
| − | - | + | - $\rm AACDBACABADAAA$ ... |
| − | + | + | + $\rm ACBCCCACAACCD$ ... |
| Zeile 63: | Zeile 69: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Die mittlere Codewortlänge ergibt sich allgemein zu | |
:$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | :$$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | Sind die vier Quellensymbole gleichwahrscheinlich $($alle Wahrscheinlichkeiten genau $1/4)$, so kann dafür auch geschrieben werden: | |
| − | :$$L_{\rm M} = 1/4 \cdot | + | :$$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | :* Code C1: | + | * $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/Quellensymbol$, |
| + | * $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$ | ||
| + | * $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Mit der Codetabelle $\text{C1}$ ergibt sich unabhängig von den Symbolwahrscheinlichkeiten stets die mittlere Codewortlänge $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \ \rm bit/Quellensymbol$. | ||
| + | |||
| + | Für die beiden anderen Codes erhält man: | ||
| + | * $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/Quellensymbol$, | ||
| + | * $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/Quellensymbol$. | ||
| + | |||
| + | |||
| + | Man erkennt aus dem Beispiel das Prinzip: | ||
| + | *Wahrscheinliche Symbole werden durch wenige Binärsymbole dargestellt, unwahrscheinliche durch mehr. | ||
| + | *Bei gleichwahrscheinlichen Symbolen wählt man am besten auch die Codewortlängen gleich. | ||
| + | |||
| − | |||
| − | |||
| − | + | '''(3)''' Richtig ist der <u>Lösungsvorschlag 1</u>: | |
| + | *Der Code $\text{C1}$ mit einheitlicher Länge aller Codeworte ist präfixfrei, | ||
| + | *aber auch andere Codes können präfixfrei sein, zum Beispiel die Codes $\text{C2}$ und $\text{C3}$. | ||
| − | |||
| − | |||
| − | : | + | '''(4)''' Richtig ist der <u>Lösungsvorschlag 1</u>: |
| + | *Bereits aus „00” am Anfang erkennt man, dass der Code $\text{C2}$ hier nicht in Frage kommt, da sonst die Quellensymbolfolge mit „AA” beginnen müsste. | ||
| + | *Tatsächlich wurde der Code $\text{C1}$ verwendet. | ||
| − | |||
| − | |||
| − | + | '''(5)''' Richtig ist der <u>Lösungsvorschlag 2</u>: | |
| + | *Der erste Lösungsvorschlag gibt dagegen die Quellensymbolfolge für den Code $\text{C2}$ an, wenn die Codesymbolfolge $\rm 001101111001100100111000$ lauten würde. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Informationstheorie | + | [[Category:Aufgaben zu Informationstheorie|^2.1 Allgemeine Beschreibung^]] |
Aktuelle Version vom 7. Juli 2021, 15:53 Uhr
Ziel von Datenkomprimierung ist es, die Nachricht einer Quelle mit möglichst wenigen Binärzeichen darzustellen.
Wir betrachten hier eine wertdiskrete Nachrichtenquelle mit dem Symbolvorrat $\rm \{ A, \ B, \ C, \ D\}$ ⇒ Symbolumfang $M = 4$ und den Auftrittswahrscheinlichkeiten
- $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 1/4$ (Teilaufgabe 1),
- $p_{\rm A} = 1/2, \, p_{\rm B} = 1/4, \, p_{\rm C} = p_{\rm D} = 1/8$ (ab Teilaufgabe 2).
Vorausgesetzt wird, dass es zwischen den einzelnen Quellensymbolen keine statistischen Bindungen gibt.
Ein Maß für die Güte eines Komprimierungsverfahrens ist die mittlere Codewortlänge $L_{\rm M}$ mit der Zusatzeinheit „bit/Quellensymbol”.
Vorgegeben sind drei Zuordnungen. Anzumerken ist:
- Jeder dieser Binärcodes $\rm C1$, $\rm C2$ und $\rm C3$ ist für eine spezielle Quellenstatistik ausgelegt.
- Alle Codes sind präfixfrei und somit ohne weitere Angabe sofort decodierbar.
Hinweis:
- Die Aufgabe gehört zum Kapitel Allgemeine Beschreibung der Quellencodierung.
Fragebogen
Musterlösung
- $$L_{\rm M} = p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B}+ p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}.$$
Sind die vier Quellensymbole gleichwahrscheinlich $($alle Wahrscheinlichkeiten genau $1/4)$, so kann dafür auch geschrieben werden:
- $$L_{\rm M} = 1/4 \cdot ( L_{\rm A} + L_{\rm B}+ L_{\rm C} + L_{\rm D}) \hspace{0.05cm}.$$
- $\text{Code C1:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.00}\ \rm bit/Quellensymbol$,
- $\text{Code C2:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$
- $\text{Code C3:}$ $L_{\rm M} \hspace{0.15cm}\underline{= 2.25}\ \rm bit/Quellensymbol$.
(2) Mit der Codetabelle $\text{C1}$ ergibt sich unabhängig von den Symbolwahrscheinlichkeiten stets die mittlere Codewortlänge $L_{\rm M} \hspace{0.15cm}\underline{= 2}\ \ \rm bit/Quellensymbol$.
Für die beiden anderen Codes erhält man:
- $\text{Code C2:}$ $L_{\rm M} = 1/2 \cdot 1 + 1/4 \cdot 2 + 1/8 \cdot 3 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 1.75}\ \rm bit/Quellensymbol$,
- $\text{Code C3:}$ $L_{\rm M} = 1/2 \cdot 3 + 1/4 \cdot 2 + 1/8 \cdot 1 + 1/8 \cdot 3 \hspace{0.15cm}\underline{= 2.50}\ \rm bit/Quellensymbol$.
Man erkennt aus dem Beispiel das Prinzip:
- Wahrscheinliche Symbole werden durch wenige Binärsymbole dargestellt, unwahrscheinliche durch mehr.
- Bei gleichwahrscheinlichen Symbolen wählt man am besten auch die Codewortlängen gleich.
(3) Richtig ist der Lösungsvorschlag 1:
- Der Code $\text{C1}$ mit einheitlicher Länge aller Codeworte ist präfixfrei,
- aber auch andere Codes können präfixfrei sein, zum Beispiel die Codes $\text{C2}$ und $\text{C3}$.
(4) Richtig ist der Lösungsvorschlag 1:
- Bereits aus „00” am Anfang erkennt man, dass der Code $\text{C2}$ hier nicht in Frage kommt, da sonst die Quellensymbolfolge mit „AA” beginnen müsste.
- Tatsächlich wurde der Code $\text{C1}$ verwendet.
(5) Richtig ist der Lösungsvorschlag 2:
- Der erste Lösungsvorschlag gibt dagegen die Quellensymbolfolge für den Code $\text{C2}$ an, wenn die Codesymbolfolge $\rm 001101111001100100111000$ lauten würde.