Aufgaben:Aufgabe 2.10: Shannon-Fano-Codierung: Unterschied zwischen den Versionen
Markus (Diskussion | Beiträge) |
|||
| (13 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Informationstheorie | + | {{quiz-Header|Buchseite=Informationstheorie/Weitere Quellencodierverfahren |
}} | }} | ||
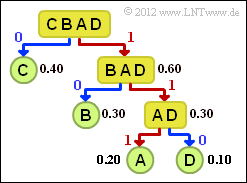
| − | [[Datei:P_ID2465__Inf_A_2_10.png |right|]] | + | [[Datei:P_ID2465__Inf_A_2_10.png |right|frame|Baumdiagramm der <br>Shannon–Fano–Codierung]] |
| − | Ein weiterer Algorithmus zur Entropiecodierung wurde 1949 von Claude Elwood Shannon und Robert Fano angegeben, der im Theorieteil beschrieben ist. | + | Ein weiterer Algorithmus zur Entropiecodierung wurde 1949 von [https://de.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] und [https://de.wikipedia.org/wiki/Robert_Fano Robert Fano] angegeben, der im Theorieteil beschrieben ist. |
| − | Diese spezielle Art von Quellencodierung soll hier an einem einfachen Beispiel für den Symbolumfang | + | Diese spezielle Art von Quellencodierung soll hier an einem einfachen Beispiel für den Symbolumfang $M = 4$ und die folgenden Symbolwahrscheinlichkeiten beschrieben werden: |
| − | :$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0. | + | :$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} |
p_{\rm D}= 0.1 \hspace{0.05cm}. $$ | p_{\rm D}= 0.1 \hspace{0.05cm}. $$ | ||
| − | Die | + | Die Grafik zeigt das dazugehörige Baumdiagramm. Man geht folgendermaßen vor: |
| − | :1. Man ordnet die Symbole nach fallender Auftrittswahrscheinlichkeit, hier | + | :1. Man ordnet die Symbole nach fallender Auftrittswahrscheinlichkeit, hier $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$. |
| − | :2. Man teilt die Symbole in zwei etwa gleichwahrscheinliche Gruppen ein, hier | + | :2. Man teilt die Symbole in zwei etwa gleichwahrscheinliche Gruppen ein, hier $\rm C$ und $\rm BAD$. |
| − | :3. Der unwahrscheinlicheren Gruppe wird das Binärsymbol <b>0</b>, der anderen die <b>1</b> zugeordnet. | + | :3. Der unwahrscheinlicheren Gruppe wird das Binärsymbol <b>0</b>, der anderen Gruppe die <b>1</b> zugeordnet. |
:4. Sind in einer Gruppe mehr als ein Zeichen, so ist der Algorithmus rekursiv anzuwenden. | :4. Sind in einer Gruppe mehr als ein Zeichen, so ist der Algorithmus rekursiv anzuwenden. | ||
| − | Für dieses Beispiel ergibt sich die folgende Codezuordnung ( | + | Für dieses Beispiel ergibt sich die folgende Codezuordnung (im Baumdiagramm markiert eine rote Verbindung eine <b>1</b> und eine blaue eine <b>0</b>): |
| − | : | + | : $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. |
Damit ergibt sich für die mittlere Codewortlänge: | Damit ergibt sich für die mittlere Codewortlänge: | ||
:$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$ | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$ | ||
| − | Der Huffman-Algorithmus würde hier zwar einen geringfügig anderen Code erzeugen, aber auch bei diesem würde | + | Der Huffman-Algorithmus würde hier zwar einen geringfügig anderen Code erzeugen, aber auch bei diesem würde |
| + | *$\rm C$ mit einem Bit, | ||
| + | *$\rm B$ mit zwei Bit und | ||
| + | *$\rm A$ und $\rm D$ mit jeweils drei Bit | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | codiert. Damit ergäbe sich ebenfalls $L_{\rm M} = 1.9 \ \rm bit/Quellensymbol$. | |
| − | <b> | + | In dieser Aufgabe sollen Sie den Shannon–Fano–Code für $M = 8$ und die Wahrscheinlichkeiten |
| + | :$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | ||
| + | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$ | ||
| + | ermitteln. Sie werden erkennen, dass sich mit diesen Wahrscheinlichkeiten „Shannon–Fano” auch hinsichtlich der Effizienz von „Huffman” unterscheiden wird. | ||
| + | |||
| + | Beim Huffman–Code ergibt sich mit den vorliegenden Wahrscheinlichkeiten die folgende Zuordnung: | ||
| + | |||
| + | : $\rm A$ → <b>100</b>, $\rm B$ → <b>0</b>, $\rm C$ → <b>111100</b>, $\rm D$ → <b>101</b>, $\rm E$ → <b>110</b>, $\rm F$ → <b>111101</b>, $\rm G$ → <b>11111</b>, $\rm H$ → <b>1110</b>. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Informationstheorie/Weitere_Quellencodierverfahren|Weitere Quellencodierverfahren]]. | ||
| + | *Insbesondere wird Bezug genommen auf die Seite [[Informationstheorie/Weitere_Quellencodierverfahren#Der_Shannon.E2.80.93Fano.E2.80.93Algorithmus|Der Shannon-Fano-Algorithmus]]. | ||
| + | *Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das folgende Interaktionsmodul: [[Applets:Huffman_Shannon_Fano|Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version]]. | ||
| + | |||
| − | |||
| Zeile 46: | Zeile 61: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie groß ist die mittlere Codewortlänge beim Huffman–Code? | + | {Wie groß ist die mittlere Codewortlänge $L_{\rm M}$ beim <u>Huffman–Code</u>? |
|type="{}"} | |type="{}"} | ||
| − | + | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/Quellensymbol$ | |
| − | {Was geschieht im ersten Schritt der Shannon–Fano–Codierung? Alle anderen Symbole werden in der zweiten Gruppe zusammengefasst. | + | {Was geschieht im ersten Schritt der <u>Shannon–Fano–Codierung</u>? <u>Hinweis</u>: Alle anderen Symbole werden in der zweiten Gruppe zusammengefasst. |
| − | |type=" | + | |type="()"} |
| − | - Man fasst | + | - Man fasst $\rm A$ und $\rm B$ zur ersten Gruppe zusammen. |
| − | + Man fasst | + | + Man fasst $\rm B$ und $\rm E$ zur ersten Gruppe zusammen. |
| − | - Die erste Gruppe besteht nur aus dem Symbol | + | - Die erste Gruppe besteht nur aus dem Symbol $\rm B$. |
| − | {Welche Zuordnungen ergeben sich für den Shannon–Fano–Algorithmus? | + | {Welche Zuordnungen ergeben sich für den <u>Shannon–Fano–Algorithmus</u>? |
|type="[]"} | |type="[]"} | ||
| − | + Das Zeichen | + | + Das Zeichen $\rm A$ wird binär mit <b>010</b> codiert. |
| − | + Das Zeichen | + | + Das Zeichen $\rm B$ wird binär mit <b>11</b> codiert. |
| − | + Das Zeichen | + | + Das Zeichen $\rm C$ wird binär mit <b>00110</b> codiert. |
| − | {Wie groß ist die mittlere Codewortlänge beim Shannon–Fano–Code? | + | {Wie groß ist die mittlere Codewortlänge $L_{\rm M}$ beim <u>Shannon–Fano–Code</u>? |
|type="{}"} | |type="{}"} | ||
| − | + | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/Quellensymbol$ | |
{Welche Aussagen gelten für beliebige Wahrscheinlichkeiten? | {Welche Aussagen gelten für beliebige Wahrscheinlichkeiten? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - $L_{\rm M}$ könnte bei „Shannon–Fano” kleiner sein als bei „Huffman”. |
| − | + | + | + $L_{\rm M}$ könnte bei „Shannon–Fano” größer sein als bei „Huffman”. |
| − | + | + | + $L_{\rm M}$ könnte bei „Shannon–Fano” und „Huffman” gleich groß sein. |
| Zeile 82: | Zeile 97: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' Für den angegebenen Huffman–Code erhält man: | |
| − | :$$L_{\rm M | + | :$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$ |
| + | |||
| + | |||
| − | < | + | '''(2)''' Richtig ist die <u>Antwort 2</u>: |
| + | *Vor Anwendung des Shannon–Fano–Algorithmus müssen die Zeichen erst nach ihren Auftrittswahrscheinlichkeiten sortiert werden. Damit ist die Antwort 1 falsch. | ||
| + | *Alle sortierten Zeichen müssen so in zwei Gruppen eingeteilt werden, dass die Gruppenwahrscheinlichkeiten möglichst gleich sind. Für den ersten Schritt: | ||
| − | |||
:$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | ||
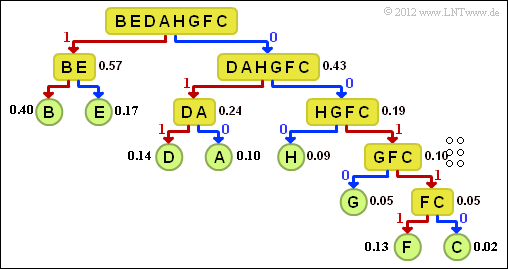
| − | Bei der Aufteilung gemäß Lösungsvorschlag 3 würde die Gleichverteilung noch weniger erreicht: | + | [[Datei:P_ID2466__Inf_A_2_10c.png|right|frame|Baumdiagramm der Shannon–Fano–Codierung]] |
| + | *Bei der Aufteilung gemäß Lösungsvorschlag 3 würde die Gleichverteilung noch weniger erreicht: | ||
:$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <b> | + | '''(3)''' <u>Alle Lösungsvorschläge</u> sind richtig: |
| − | :$$L_{\rm M | + | *Die Grafik zeigt das Baumdiagramm der Shannon–Fano–Codierung. |
| + | *Daraus ergibt sich folgende Zuordnung (eine rote Verbindung weist auf eine <b>1</b> hin, eine blaue auf eine <b>0</b>): | ||
| + | : $\underline{\rm A}$ → <u><b>010</b></u>, $\underline{\rm B}$ → <u><b>11</b></u>, $\underline{\rm C}$ → <u><b>00110</b></u>, | ||
| + | : ${\rm D}$ → <b>011</b>, ${\rm E}$ → <b>10</b>, ${\rm F}$ → <b>00111</b>, ${\rm G}$ → <b>0010</b>, ${\rm H}$ → <b>000</b>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Mit dem Ergebnis der Teilaufgabe '''(3)''' erhält man: | ||
| + | :$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$ | ||
| + | |||
| + | |||
| − | + | '''(5)''' Richtig sind die <u>Aussagen 2 und 3</u>: | |
| + | *Im vorliegenden Beispiel ergibt sich bei Shannon–Fano ein ungünstigerer Wert als bei Huffman. | ||
| + | *In den meisten Fällen – so auch im Beispiel auf der Angabenseite – ergibt sich für Huffman und Shannon–Fano ein gleichwertiger Code und damit auch die gleiche mittlere Codewortlänge. | ||
| + | *Einen effektiveren Code als Huffman liefert Shannon–Fano dagegen nie. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 12. August 2021, 12:59 Uhr
Ein weiterer Algorithmus zur Entropiecodierung wurde 1949 von Claude Elwood Shannon und Robert Fano angegeben, der im Theorieteil beschrieben ist.
Diese spezielle Art von Quellencodierung soll hier an einem einfachen Beispiel für den Symbolumfang $M = 4$ und die folgenden Symbolwahrscheinlichkeiten beschrieben werden:
- $$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$
Die Grafik zeigt das dazugehörige Baumdiagramm. Man geht folgendermaßen vor:
- 1. Man ordnet die Symbole nach fallender Auftrittswahrscheinlichkeit, hier $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.
- 2. Man teilt die Symbole in zwei etwa gleichwahrscheinliche Gruppen ein, hier $\rm C$ und $\rm BAD$.
- 3. Der unwahrscheinlicheren Gruppe wird das Binärsymbol 0, der anderen Gruppe die 1 zugeordnet.
- 4. Sind in einer Gruppe mehr als ein Zeichen, so ist der Algorithmus rekursiv anzuwenden.
Für dieses Beispiel ergibt sich die folgende Codezuordnung (im Baumdiagramm markiert eine rote Verbindung eine 1 und eine blaue eine 0):
- $\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.
Damit ergibt sich für die mittlere Codewortlänge:
- $$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
Der Huffman-Algorithmus würde hier zwar einen geringfügig anderen Code erzeugen, aber auch bei diesem würde
- $\rm C$ mit einem Bit,
- $\rm B$ mit zwei Bit und
- $\rm A$ und $\rm D$ mit jeweils drei Bit
codiert. Damit ergäbe sich ebenfalls $L_{\rm M} = 1.9 \ \rm bit/Quellensymbol$.
In dieser Aufgabe sollen Sie den Shannon–Fano–Code für $M = 8$ und die Wahrscheinlichkeiten
- $$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$
ermitteln. Sie werden erkennen, dass sich mit diesen Wahrscheinlichkeiten „Shannon–Fano” auch hinsichtlich der Effizienz von „Huffman” unterscheiden wird.
Beim Huffman–Code ergibt sich mit den vorliegenden Wahrscheinlichkeiten die folgende Zuordnung:
- $\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.
Hinweise:
- Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
- Insbesondere wird Bezug genommen auf die Seite Der Shannon-Fano-Algorithmus.
- Zur Kontrolle Ihrer Ergebnisse verweisen wir auf das folgende Interaktionsmodul: Huffman- und Shannon-Fano-Codierung ⇒ $\text{SWF}$–Version.
Fragebogen
Musterlösung
- $$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
(2) Richtig ist die Antwort 2:
- Vor Anwendung des Shannon–Fano–Algorithmus müssen die Zeichen erst nach ihren Auftrittswahrscheinlichkeiten sortiert werden. Damit ist die Antwort 1 falsch.
- Alle sortierten Zeichen müssen so in zwei Gruppen eingeteilt werden, dass die Gruppenwahrscheinlichkeiten möglichst gleich sind. Für den ersten Schritt:
- $${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$
- Bei der Aufteilung gemäß Lösungsvorschlag 3 würde die Gleichverteilung noch weniger erreicht:
- $${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$
(3) Alle Lösungsvorschläge sind richtig:
- Die Grafik zeigt das Baumdiagramm der Shannon–Fano–Codierung.
- Daraus ergibt sich folgende Zuordnung (eine rote Verbindung weist auf eine 1 hin, eine blaue auf eine 0):
- $\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,
- ${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.
(4) Mit dem Ergebnis der Teilaufgabe (3) erhält man:
- $$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$
(5) Richtig sind die Aussagen 2 und 3:
- Im vorliegenden Beispiel ergibt sich bei Shannon–Fano ein ungünstigerer Wert als bei Huffman.
- In den meisten Fällen – so auch im Beispiel auf der Angabenseite – ergibt sich für Huffman und Shannon–Fano ein gleichwertiger Code und damit auch die gleiche mittlere Codewortlänge.
- Einen effektiveren Code als Huffman liefert Shannon–Fano dagegen nie.