Aufgaben:Aufgabe 2.1Z: ZSB-AM ohne/mit Träger: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
|||
| (15 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Modulationsverfahren/ Zweiseitenband-Amplitudenmodulation | + | {{quiz-Header|Buchseite=Modulationsverfahren/Zweiseitenband-Amplitudenmodulation |
}} | }} | ||
| − | [[Datei:|right|]] | + | [[Datei:P_ID987__Mod_Z_2_1.png|right|frame|Die bei dieser AM beteiligten Signale]] |
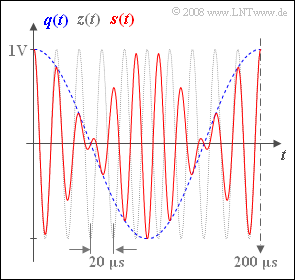
| + | Die Grafik zeigt als rote Kurve einen Ausschnitt des Sendesignals $s(t) = q(t) · z(t)$ einer Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $\rm 200 \ µ s$. | ||
| + | |||
| + | Zusätzlich sind in der Grafik eingetragen: | ||
| + | *das Quellensignal (als blau–gestrichelte Kurve): | ||
| + | :$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$ | ||
| + | *das Trägersignal (grau–gepunkteter Verlauf): | ||
| + | :$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$ | ||
| + | |||
| + | Ab der Teilaufgabe '''(4)''' wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_{\rm T} = 2\text{ V}$: | ||
| + | :$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation|Zweiseitenband-Amplitudenmodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seiten [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#Beschreibung_im_Zeitbereich|Beschreibung im Zeitbereich]] und [[Modulationsverfahren/Zweiseitenband-Amplitudenmodulation#ZSB-Amplitudenmodulation_mit_Tr.C3.A4ger|ZSB-Amplitudenmodulation mit Träger]]. | ||
| + | |||
| + | |||
| Zeile 9: | Zeile 29: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Ermitteln Sie aus der Grafik die Phasenwerte von Quellen– und Trägersignal. |
| + | |type="{}"} | ||
| + | $\phi_{\rm N} \ = \ $ { 0. } $\ \text{Grad}$ | ||
| + | $\phi_{\rm T} \ = \ $ { 0. } $\ \text{Grad}$ | ||
| + | |||
| + | {Welche Frequenz $f_{\rm N}$ besitzt das Nachrichtensignal $q(t)$ und welche Frequenz $f_{\rm T}$ das Trägersignal $z(t)$? | ||
| + | |type="{}"} | ||
| + | $f_{\rm N} \ = \ $ { 5 3% } $\ \text{kHz}$ | ||
| + | $f_{\rm T} \ = \ $ { 50 3% } $\ \text{kHz}$ | ||
| + | |||
| + | {Analysieren Sie die Nulldurchgänge von $s(t)$. Welche Aussagen treffen zu? | ||
|type="[]"} | |type="[]"} | ||
| − | + | + Alle Nulldurchgänge von $z(t)$ bleiben in $s(t)$ erhalten. | |
| − | + | + | + Es gibt weitere Nullstellen, verursacht durch $q(t)$. |
| + | - Es gilt $s(t) = a(t) · \cos(ω_T · t)$ mit $a(t) = |q(t)|$. | ||
| + | {Bestimmen Sie die Spektralfunktion $S(f)$ über die Faltung. Welche (positiven) Frequenzen $f_1$ und $f_2 > f_1$ sind im Signal enthalten? | ||
| + | |type="{}"} | ||
| + | $f_1 \ = \ $ { 45 3% } $\ \text{kHz}$ | ||
| + | $f_2\ = \ $ { 55 3% } $\ \text{kHz}$ | ||
| − | { | + | {Es gelte nun $A_{\rm T} = 2\text{ V}$. Wie groß ist der Modulationsgrad $m$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $m \ = \ $ { 0.5 3% } |
| − | |||
| + | {Welche der Aussagen treffen bei der „ZSB–AM mit Träger” und $A_{\rm T} = 2\text{ V}$ zu? | ||
| + | |type="[]"} | ||
| + | + $S(f)$ beinhaltet nun auch Diracfunktionen bei $±f_{\rm T}$. | ||
| + | - Die Gewichte dieser Diraclinien sind jeweils $2\text{ V}$. | ||
| + | + $q(t)$ ist in der Hüllkurve von $s(t)$ zu erkennen. | ||
| + | - Durch den zusätzlichen Trägeranteil bleibt die Leistung unverändert. | ||
</quiz> | </quiz> | ||
| Zeile 25: | Zeile 65: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Beide Signale sind cosinusförmig ⇒ $ϕ_{\rm N} \hspace{0.15cm}\underline { = 0}$ und $ϕ_{\rm T} \hspace{0.15cm}\underline { = 0}$. |
| − | '''2 | + | |
| − | '''3 | + | |
| − | '''4 | + | '''(2)''' Aus der Grafik können für $q(t)$ und $z(t)$ die Periodendauern $200$ μs bzw. $20$ μs abgelesen werden. |
| − | ''' | + | *Daraus ergeben sich die Frequenzen zu $f_{\rm N} \hspace{0.15cm}\underline { = 5}$ kHz und $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz. |
| − | ''' | + | |
| − | ''' | + | |
| + | '''(3)''' Richtig sind die <u>Lösungsvorschläge 1 und 2</u>: | ||
| + | *Die Nullstellen von $z(t)$ bei $±5$ μs, $±15$ μs, $±25$ μs, ... sind auch im Signal $s(t)$ vorhanden ⇒ Aussage 1 ist richtig. | ||
| + | *Weitere Nullstellen von $s(t)$ – verursacht durch $q(t)$ – liegen bei $±50$ μs, $±150$ μs, $±250$ μs, .... ⇒ Aussage 2 ist richtig. | ||
| + | *Die dritte Aussage trifft dagegen nicht zu, sondern es gilt: $ s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$ | ||
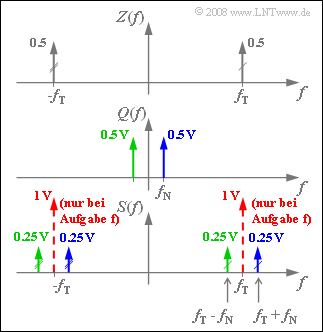
| + | [[Datei:P_ID988__Mod_Z_2_1_d.png|right|frame|ZSB–AM–Spektrum $Z(f)$, $Q(f)$ und $S(f)$]] | ||
| + | |||
| + | *Für $q(t) > 0$ ist die Phasenfunktion $ϕ(t) = 0$ und $s(t)$ ist gleichlaufend mit $z(t)$. | ||
| + | *Dagegen gilt für $q(t) < 0$: $ϕ(t) = π = 180^\circ$. | ||
| + | *Bei den Nulldurchgängen von $q(t)$ weist das modulierte Signal $s(t)$ Phasensprünge auf. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Das Spektrum $S(f)$ ergibt sich aus der Faltung der Spektren $Z(f)$ und $Q(f)$, die jeweils aus nur zwei Diracfunktionen bestehen. Die Grafik zeigt das Ergebnis. | ||
| + | *Die rot gezeichneten Diracs gelten nur für die „ZSB–AM mit Träger” und beziehen sich auf die Frage '''(6)'''. | ||
| + | *Die Faltung der beiden $Z(f)$–Diracfunktionen bei $f_{\rm T} = 50\text{ kHz}$ mit $Q(f)$ führt zu den Diraclinien bei $f_{\rm T} - f_{\rm N}$ und $f_{\rm T} + f_{\rm N}$, jeweils mit Gewicht $0.5 · 0.5\text{ V}= 0.25\text{ V}$. | ||
| + | *Die gesuchten Werte sind somit $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$ und $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$. | ||
| + | *Die mit zwei Markierungsstrichen versehene Diracfunktion $0.5 · δ(f + f_{\rm T})$ führt zu zwei weiteren Diraclinien bei $-f_1$ und $-f_2$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(5)''' Der Modulationsgrad berechnet sich zu: | ||
| + | :$$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(6)''' Richtig sind die <u>Lösungsvorschläge 1 und 3</u>: | ||
| + | *Gemäß der Skizze ergeben sich Diraclinien bei $±f_{\rm T}$, beide mit dem Impulsgewicht $A_{\rm T}/2 = 1\text{ V}$. | ||
| + | *Bei $m ≤ 1$ ist $q(t)$ in der Hüllkurve erkennbar und Hüllkurvendemodulation anwendbar. | ||
| + | *Allerdings muss diese einfachere Empfängervariante durch eine sehr viel größere Sendeleistung erkauft werden. | ||
| + | *In diesem Beispiel $(m = 0.5)$ wird die Sendeleistung durch den Trägerzusatz verneunfacht. | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Modulationsverfahren|^2.1 | + | [[Category:Aufgaben zu Modulationsverfahren|^2.1 ZSB-Amplitudenmodulation^]] |
Aktuelle Version vom 29. November 2021, 15:10 Uhr
Die Grafik zeigt als rote Kurve einen Ausschnitt des Sendesignals $s(t) = q(t) · z(t)$ einer Zweiseitenband–Amplitudenmodulation (abgekürzt mit ZSB-AM) ohne Träger. Die Dauer des Zeitausschnitts beträgt $\rm 200 \ µ s$.
Zusätzlich sind in der Grafik eingetragen:
- das Quellensignal (als blau–gestrichelte Kurve):
- $$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$
- das Trägersignal (grau–gepunkteter Verlauf):
- $$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$
Ab der Teilaufgabe (4) wird die „ZSB–AM mit Träger” betrachtet. Dann gilt mit $A_{\rm T} = 2\text{ V}$:
- $$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
- Bezug genommen wird insbesondere auf die Seiten Beschreibung im Zeitbereich und ZSB-Amplitudenmodulation mit Träger.
Fragebogen
Musterlösung
(2) Aus der Grafik können für $q(t)$ und $z(t)$ die Periodendauern $200$ μs bzw. $20$ μs abgelesen werden.
- Daraus ergeben sich die Frequenzen zu $f_{\rm N} \hspace{0.15cm}\underline { = 5}$ kHz und $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz.
(3) Richtig sind die Lösungsvorschläge 1 und 2:
- Die Nullstellen von $z(t)$ bei $±5$ μs, $±15$ μs, $±25$ μs, ... sind auch im Signal $s(t)$ vorhanden ⇒ Aussage 1 ist richtig.
- Weitere Nullstellen von $s(t)$ – verursacht durch $q(t)$ – liegen bei $±50$ μs, $±150$ μs, $±250$ μs, .... ⇒ Aussage 2 ist richtig.
- Die dritte Aussage trifft dagegen nicht zu, sondern es gilt: $ s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$
- Für $q(t) > 0$ ist die Phasenfunktion $ϕ(t) = 0$ und $s(t)$ ist gleichlaufend mit $z(t)$.
- Dagegen gilt für $q(t) < 0$: $ϕ(t) = π = 180^\circ$.
- Bei den Nulldurchgängen von $q(t)$ weist das modulierte Signal $s(t)$ Phasensprünge auf.
(4) Das Spektrum $S(f)$ ergibt sich aus der Faltung der Spektren $Z(f)$ und $Q(f)$, die jeweils aus nur zwei Diracfunktionen bestehen. Die Grafik zeigt das Ergebnis.
- Die rot gezeichneten Diracs gelten nur für die „ZSB–AM mit Träger” und beziehen sich auf die Frage (6).
- Die Faltung der beiden $Z(f)$–Diracfunktionen bei $f_{\rm T} = 50\text{ kHz}$ mit $Q(f)$ führt zu den Diraclinien bei $f_{\rm T} - f_{\rm N}$ und $f_{\rm T} + f_{\rm N}$, jeweils mit Gewicht $0.5 · 0.5\text{ V}= 0.25\text{ V}$.
- Die gesuchten Werte sind somit $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$ und $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$.
- Die mit zwei Markierungsstrichen versehene Diracfunktion $0.5 · δ(f + f_{\rm T})$ führt zu zwei weiteren Diraclinien bei $-f_1$ und $-f_2$.
(5) Der Modulationsgrad berechnet sich zu:
- $$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(6) Richtig sind die Lösungsvorschläge 1 und 3:
- Gemäß der Skizze ergeben sich Diraclinien bei $±f_{\rm T}$, beide mit dem Impulsgewicht $A_{\rm T}/2 = 1\text{ V}$.
- Bei $m ≤ 1$ ist $q(t)$ in der Hüllkurve erkennbar und Hüllkurvendemodulation anwendbar.
- Allerdings muss diese einfachere Empfängervariante durch eine sehr viel größere Sendeleistung erkauft werden.
- In diesem Beispiel $(m = 0.5)$ wird die Sendeleistung durch den Trägerzusatz verneunfacht.