Digitalsignalübertragung/Approximation der Fehlerwahrscheinlichkeit: Unterschied zwischen den Versionen
Ayush (Diskussion | Beiträge) |
|||
| (39 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
| − | == Optimale Entscheidung bei binärer Übertragung | + | == Optimale Entscheidung bei binärer Übertragung== |
<br> | <br> | ||
| − | Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: | + | Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: $\boldsymbol{r} = \boldsymbol{s} + \boldsymbol{n}$. Dieses System weist folgende Eigenschaften auf: |
| − | *Der das Übertragungssystem vollständig beschreibende Vektorraum wird von | + | *Der das Übertragungssystem vollständig beschreibende Vektorraum wird von $N = 2$ zueinander orthogonalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ aufgespannt.<br> |
| − | *Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor | + | *Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$.<br> |
| − | *Es gibt nur zwei mögliche Sendesignale ( | + | *Es gibt nur zwei mögliche Sendesignale $(M = 2)$, die durch die beiden Vektoren $\boldsymbol{ s_0} = (s_{01},\hspace{0.05cm}s_{02})$ und $\boldsymbol{ s_1} = (s_{11},\hspace{0.05cm}s_{12})$ beschrieben werden: |
| + | [[Datei:P ID2019 Dig T 4 3 S1 version1.png|right|frame|Entscheidungsregionen für gleiche (links) bzw. ungleiche (rechts) Auftrittswahrscheinlichkeiten|class=fit]] | ||
| + | :$$s_0(t)= s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},$$ | ||
| + | :$$s_1(t) = s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.$$ | ||
| − | + | *Die beiden Nachrichten $m_0 \ \Leftrightarrow \ \boldsymbol{ s_0}$ und $m_1 \ \Leftrightarrow \ \boldsymbol{ s_1}$ sind nicht notwendigermaßen gleichwahrscheinlich.<br> | |
| − | |||
| − | * | + | *Aufgabe des Entscheiders ist es, einen Schätzwert für den Empfangsvektor $\boldsymbol{r}$ nach der [[Digitalsignalübertragung/Struktur_des_optimalen_Empfängers#Fundamentaler_Ansatz_zum_optimalen_Empf.C3.A4ngerentwurf |"MAP–Entscheidungsregel"]] anzugeben. Diese lautet im vorliegenden Fall mit $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2) |
| + | \hspace{0.05cm}$: | ||
| + | :$$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm}|\hspace{0.05cm} m_i )\big ] | ||
| + | \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\} | ||
| + | \hspace{0.05cm}.$$ | ||
| − | * | + | *Im betrachteten Sonderfall $N = 2$ und $M = 2$ partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete $I_0$ (rot hinterlegt) und $I_1$ (blau), wie die nebenstehende Grafik verdeutlicht. |
| − | + | *Liegt der Empfangswert in $I_0$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | {{BlaueBox|TEXT= |
| − | + | $\text{Herleitung und Bildbeschreibung:}$ | |
| − | Beim AWGN–Kanal und | + | Beim AWGN–Kanal und $M = 2$ lautet somit die Entscheidungsregel: |
| − | : | + | ⇒ Man entscheide sich immer dann für die Nachricht $m_0$, falls folgende Bedingung erfüllt ist: |
| − | |||
| − | |||
| − | + | :$${\rm Pr}( m_0) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 \right ] | |
| + | > {\rm Pr}( m_1) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 \right ] | ||
| + | \hspace{0.05cm}.$$ | ||
| − | : | + | ⇒ Die Grenzlinie zwischen den beiden Entscheidungsregionen $I_0$ und $I_1$ erhält man, wenn man in obiger Gleichung das Größerzeichen durch das Gleichheitszeichen ersetzt und die Gleichung etwas umformt: |
| − | |||
| − | : | + | :$$\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_0)\big ] = |
| + | \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_1)\big ]$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 | ||
| + | + 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_0)}{ {\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ | ||
| − | Aus dieser | + | Aus dieser Darstellung erkennt man: |
| − | *Die Grenzkurve zwischen den Regionen | + | *Die Grenzkurve zwischen den Regionen $I_0$ und $I_1$ ist eine Gerade, da die Bestimmungsgleichung linear im Empfangsvektor $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2)$ ist.<br> |
| − | *Bei gleichwahrscheinlichen Symbolen verläuft die Grenze genau in der Mitte zwischen | + | *Bei gleichwahrscheinlichen Symbolen verläuft die Grenze genau in der Mitte zwischen $\boldsymbol{ s }_0$ und $\boldsymbol{ s }_1$ und um $90^\circ$ verdreht gegenüber der Verbindungslinie zwischen diesen Sendepunkten (linke Grafik): |
| − | : | + | :$$\vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert ^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert ^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$ |
| − | *Für Pr( | + | *Für ${\rm Pr}(m_0) > {\rm Pr}(m_1)$ ist die Entscheidungsgrenze in Richtung des unwahrscheinlicheren Symbols $\boldsymbol{ s }_1$ verschoben, und zwar um so mehr, je größer die AWGN–Streuung $\sigma_n$ ist.<br> |
| − | + | *Die grün–durchgezogene Entscheidungsgrenze im rechten Bild sowie die Entscheidungsregionen $I_0$ (rot) und $I_1$ (blau) gelten für die (normierte) Streuung $\sigma_n = 1$ und die gestrichelten Grenzlinien für $\sigma_n = 0$ bzw. $\sigma_n = 2$.<br>}} | |
| − | + | ==Der Sonderfall gleichwahrscheinlicher Binärsymbolen == | |
| − | |||
| − | |||
<br> | <br> | ||
| − | Wir gehen weiterhin von einem Binärsystem aus ( | + | Wir gehen weiterhin von einem Binärsystem aus $(M = 2)$, betrachten aber nun den einfachen Fall, dass dieses durch eine einzige Basisfunktion beschrieben werden kann $(N = 1)$. Die Fehlerwahrscheinlichkeit hierfür wurde bereits im Abschnitt [[Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung#Definition_der_Bitfehlerwahrscheinlichkeit|"Definition der Bitfehlerwahrscheinlichkeit"]] berechnet.<br> |
| − | Mit der für | + | Mit der für das vierte Hauptkapitel gewählten Nomenklatur und Darstellungsform ergibt sich folgende Konstellation: |
| − | + | [[Datei:P ID2020 Dig T 4 3 S2 version1.png||right|frame|Bedingte Dichtefunktionen bei gleichwahrscheinlichen Symbolen<br><br><br>|class=fit]] | |
| − | *Die Abszisse | + | *Der Empfangswert $r = s + n$ ist nunmehr ein Skalar und setzt sich aus dem Sendesignal $s \in \{s_0, \hspace{0.05cm}s_1\}$ und dem Rauschterm $n$ additiv zusammen. Die Abszisse $\rho$ bezeichnet eine Realisierung von $r$.<br> |
| − | * | + | *Die Abszisse ist zudem auf die Bezugsgröße $\sqrt{E}$ normiert, wobei die formale Normierungsenergie $E$ keine physikalisch interpretierbare Bedeutung hat.<br> |
| − | * | + | *Der Rauschterm $n$ ist gaußverteilt mit Mittelwert $m_n = 0$ und Varianz $\sigma_n^2$. Die Wurzel aus der Varianz $(\sigma_n)$ wird als der Effektivwert oder die Streuung bezeichnet.<br> |
| − | * | + | *Die Entscheidergrenze $G$ unterteilt den gesamten Wertebereich von $r$ in die zwei Teilbereiche $I_0$ $($in dem unter anderem $s_0$ liegt$)$ und $I_1$ $($mit dem Signalwert $s_1)$.<br> |
| − | |||
| − | + | *Ist $\rho > G$, so liefert der Entscheider den Schätzwert $m_0$, andernfalls $m_1$. Hierbei ist vorausgesetzt, dass die Nachricht $m_i$ mit dem Sendesignal $s_i$ eineindeutig zusammenhängt: $m_i \Leftrightarrow s_i$. | |
| − | |||
| − | |||
| − | + | Die Grafik zeigt die bedingten (eindimensionalen) Wahrscheinlichkeitsdichtefunktionen $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_0}$ und $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_1}$ für den AWGN–Kanal, wobei gleiche Symbolwahrscheinlichkeiten vorausgesetzt sind: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Die (optimale) Entscheidergrenze ist somit $G = 0$. Man erkennt aus dieser Darstellung: | |
| + | #Ist $m = m_0$ ⇒ t $s = s_0 = 2 \cdot E^{1/2}$, so kommt es nur dann zu einer Fehlentscheidung, wenn $\eta$, die Realisierung der Rauschgröße $n$, kleiner ist als $-2 \cdot E^{1/2}$. | ||
| + | #In diesem Fall ist $\rho < 0$, wobei $\rho$ eine Realisierung des Empfangswertes $r$ bezeichnet. | ||
| + | #Bei $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$ kommt es dagegen immer dann zu einer Fehlentscheidung, wenn $\eta$ größer ist als $+2 \cdot E^{1/2}$. In diesem Fall ist $\rho > 0$. | ||
| − | |||
| − | == | + | == Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen == |
<br> | <br> | ||
| − | [[ | + | Es gelte ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Bei AWGN–Rauschen mit Effektivwert (Streuung) $\sigma_n$ erhält man, wie bereits im Abschnitt [[Digitalsignal%C3%BCbertragung/Fehlerwahrscheinlichkeit_bei_Basisband%C3%BCbertragung#Definition_der_Bitfehlerwahrscheinlichkeit| "Definition der Bitfehlerwahrscheinlichkeit"]] mit anderer Nomenklatur berechnet wurde, für die Wahrscheinlichkeit einer Fehlentscheidung $(\cal E)$ unter der Bedingung, dass die Nachricht $m_0$ gesendet wurde: |
| − | + | :$${\rm Pr}({ \cal E}\hspace{0.05cm} \vert \hspace{0.05cm} m_0) = \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } \hspace{0.05cm} \vert \hspace{0.05cm}m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}\vert\hspace{0.05cm}m_0 } ({ \eta } \hspace{0.05cm}|\hspace{0.05cm}m_0 ) \,{\rm d} \eta = \int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = | |
| − | |||
| − | |||
| − | |||
| − | |||
\int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) | \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) | ||
| − | \hspace{0.05cm}. | + | \hspace{0.05cm}.$$ |
| − | + | Bei der Herleitung der Gleichung wurde berücksichtigt, dass das AWGN–Rauschen $\eta$ unabhängig vom Signal $(m_0$ oder $m_1)$ ist und eine symmetrische WDF besitzt. Verwendet wurde zudem das komplementäre Gaußsche Fehlerintegral | |
| − | + | :$${\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u | |
| − | : | + | \hspace{0.05cm}.$$ |
| − | \hspace{0.05cm}. | ||
| − | + | Entsprechend gilt für $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$: | |
| + | :$${\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}\vert\hspace{0.05cm}m_1 } ({ \rho } \hspace{0.05cm}\vert\hspace{0.05cm}m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) | ||
| + | \hspace{0.05cm}.$$ | ||
| − | :: | + | {{BlaueBox|TEXT= |
| − | \hspace{0.05cm}. | + | $\text{Fazit:}$ Mit dem Abstand $d = s_1 - s_0$ der Signalraumpunkte kann man die Ergebnisse zusammenfassen, wobei noch ${\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$ zu berücksichtigen ist: |
| + | :$${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0) = {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = {\rm Q} \big ( {d}/(2{\sigma_n}) \big )$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1)= \big [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \big ] \cdot | ||
| + | {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] \hspace{0.05cm}.$$ | ||
| − | + | <u>Hinweise:</u> | |
| + | #Diese Gleichung gilt unter der Voraussetzung $G = 0$ ganz allgemein, also auch für ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$. | ||
| + | #Bei [[Digitalsignalübertragung/Approximation_der_Fehlerwahrscheinlichkeit#Optimale_Schwelle_bei_nicht_gleichwahrscheinlichen_Symbolen|"nicht gleichwahrscheinlichen Symbolen"]] lässt sich allerdings die Fehlerwahrscheinlichkeit durch eine andere Entscheidergrenze verkleinern.<br> | ||
| + | #Die hier genannte Gleichung gilt auch dann, wenn die Signalraumpunkte keine Skalare sind, sondern durch die Vektoren $\boldsymbol{ s}_0$ und $\boldsymbol{ s}_1$ beschrieben werden. | ||
| + | #Der Abstand $d$ ergibt sich dann als die "Norm" des Differenzvektors: $d = \vert \hspace{-0.05cm} \vert \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} \vert \hspace{-0.05cm} \vert | ||
| + | \hspace{0.05cm}.$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| + | $\text{Beispiel 1:}$ Betrachten wir nochmals die Signalraumkonstellation von der [[Digitalsignal%C3%BCbertragung/Approximation_der_Fehlerwahrscheinlichkeit#Optimale_Entscheidung_bei_bin.C3.A4rer_.C3.9Cbertragung_.281.29| ersten Kapitelseite]] (untere Grafik) mit den Werten | ||
| − | + | [[Datei:Dig_T_4_3_S2b_version2.png|right|frame|Zwei Signalraumkonstellationen|class=fit]] | |
| + | *$\boldsymbol{ s}_0/E^{1/2} = (3.6, \hspace{0.05cm}0.8)$, | ||
| − | + | *$\boldsymbol{ s}_1/E^{1/2} = (0.4, \hspace{0.05cm}3.2)$. | |
| − | \hspace{0.05cm}. | ||
| − | |||
| − | |||
| − | |||
| − | + | Hier beträgt der Abstand der Signalraumpunkte | |
| − | |||
| − | + | :$$d = \vert \hspace{-0.05cm} \vert s_1 - s_0 \vert \hspace{-0.05cm} \vert = \sqrt{E \cdot (0.4 - 3.6)^2 + E \cdot (3.2 - 0.8)^2} = 4 \cdot \sqrt {E}\hspace{0.05cm}.$$ | |
| − | + | Es ergibt sich also der genau gleiche Wert wie für die obere Konstellation mit | |
| + | *$\boldsymbol{ s}_0/E^{1/2} = (2, \hspace{0.05cm}0)$, | ||
| + | |||
| + | *$\boldsymbol{ s}_1/E^{1/2} = (-2, \hspace{0.05cm}0)$. <br> | ||
| − | |||
| − | |||
| − | + | Die Abbildungen zeigen diese beiden Konstellationen und lassen folgende Gemeinsamkeiten bzw. Unterschiede erkennen, wobei jeweils von der AWGN–Rauschvarianz $\sigma_n^2 = N_0/2$ ausgegangen wird. Die Kreise in der Grafik veranschaulichen die zirkuläre Symmetrie von 2D–AWGN–Rauschen. | |
| + | *Wie bereits gesagt, sind sowohl der Abstand der Signalpunkte von der Entscheidungsgeraden $(d/2 = 2 \cdot \sqrt {E})$ als auch der AWGN–Kennwert $\sigma_n$ in beiden Fällen gleich.<br> | ||
| − | : | + | *Daraus folgt: Die beiden Anordnungen führen zur gleichen Fehlerwahrscheinlichkeit, wenn man den Parameter $E$ (eine Art Normierungsenergie) konstant lässt: |
| − | + | :$${\rm Pr} ({\rm Symbolfehler}) = {\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ]\hspace{0.05cm}.$$ | |
| − | Auf diesen Sachverhalt wird in der Aufgabe | + | *Die "mittlere Energie pro Symbol" ⇒ $E_{\rm S}$ ergibt sich für die obere Konstellation zu |
| + | :$$E_{\rm S} = 1/2 \cdot \vert \hspace{-0.05cm} \vert s_0 \vert \hspace{-0.05cm} \vert^2 + 1/2 \cdot \vert \hspace{-0.05cm} \vert s_1 \vert \hspace{-0.05cm} \vert^2 = E/2 \cdot \big[(+2)^2 + (-2)^2\big] = 4 \cdot {E}\hspace{0.05cm}.$$ | ||
| + | *Bei der unteren Konstellation erhält man in gleicher Weise: | ||
| + | :$$E_{\rm S} = \ \text{...} \ = E/2 \cdot \big[(3.6)^2 + (0.8)^2\big] + E/2 \cdot \big[(0.4)^2 + (3.2)^2 \big] = 12 \cdot {E}\hspace{0.05cm}.$$ | ||
| + | *Bei gegebener mittlerer Energie pro Symbol $(E_{\rm S})$ ist demnach die obere Konstellation der unteren deutlich überlegen: Die gleiche Fehlerwahrscheinlichkeit ergibt sich mit einem Drittel der aufzuwendenden Energie pro Symbol. Auf diesen Sachverhalt wird in der [[Aufgaben:Aufgabe_4.06Z:_Signalraumkonstellationen|"Aufgabe 4.6Z"]] noch im Detail eingegangen. }}<br> | ||
| − | == | + | == Optimale Schwelle bei nicht gleichwahrscheinlichen Symbolen == |
<br> | <br> | ||
| − | Gilt Pr( | + | Gilt ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$, so kann man durch eine Verschiebung der Entscheidungsgrenze $G$ eine etwas kleinere Fehlerwahrscheinlichkeit erreichen. Die nachfolgenden Ergebnisse werden ausführlich in der Musterlösung zur [[Aufgaben:Aufgabe_4.07:_Nochmals_Entscheidungsgrenzen|"Aufgabe 4.7"]] hergeleitet: |
| − | *Bei ungleichen Symbolwahrscheinlichkeiten liegt die optimale Entscheidungsgrenze | + | *Bei ungleichen Symbolwahrscheinlichkeiten liegt die optimale Entscheidungsgrenze $G_{\rm opt}$ zwischen den Regionen $I_0$, $I_1$ näher beim unwahrscheinlicheren Symbol.<br> |
| − | *Die normierte optimale Verschiebung gegenüber der Grenze | + | *Die normierte optimale Verschiebung gegenüber der Grenze $G = 0$ bei gleichwahrscheinlichen Symbolen beträgt |
::<math>\gamma_{\rm opt} = \frac{G_{\rm opt}}{s_0 } = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm}.</math> | ::<math>\gamma_{\rm opt} = \frac{G_{\rm opt}}{s_0 } = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm}.</math> | ||
| Zeile 155: | Zeile 157: | ||
*Die Fehlerwahrscheinlichkeit ist dann gleich | *Die Fehlerwahrscheinlichkeit ist dann gleich | ||
| − | : | + | :$${\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Q} \big[ {d}/(2{\sigma_n}) \cdot (1 - \gamma_{\rm opt}) \big ] |
| − | + {\rm Pr}(m_1) \cdot {\rm Q} \ | + | + {\rm Pr}(m_1) \cdot {\rm Q} \big [ {d}/(2{\sigma_n}) \cdot (1 + \gamma_{\rm opt}) \big ]\hspace{0.05cm}.$$ |
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ Der formale Parameter $\rho$ (Abszisse) kennzeichnet wieder eine Realisierung der AWGN–Zufallsgröße $r = s + n$. | ||
| + | [[Datei:P ID2024 Dig T 4 3 S3 version2.png|right|frame|Dichtefunktionen für gleiche/ungleiche Symbolwahrscheinlichkeiten<br><br>|class=fit]] | ||
| + | |||
| + | Für das Folgende gelte weiter: | ||
| + | :$$\boldsymbol{ s }_0 = (2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \boldsymbol{ s }_1 = (- 2 \cdot \sqrt{E}, \hspace{0.1cm} 0)$$ | ||
| + | :$$ \Rightarrow \hspace{0.2cm} d = 2 \cdot \sqrt{E}, \hspace{0.2cm} \sigma_n = \sqrt{E} \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1)$ ergibt sich die optimale Entscheidungsgrenze zu $G_{\rm opt} = 0$ (siehe obere Skizze). Damit erhält man für die Fehlerwahrscheinlichkeit: | ||
| − | {{ | + | :$${\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} (2) \approx 2.26\% \hspace{0.05cm}.$$ |
| − | + | *Nun betrachten wir mit ${\rm Pr}( m_0) = 3/4\hspace{0.05cm},\hspace{0.1cm}{\rm Pr}( m_1) = 1/4\hspace{0.05cm}$ ungleiche Symbolwahrscheinlichkeiten (untere Skizze). Die weiteren Größen seien gegenüber der oberen Grafik unverändert. In diesem Fall beträgt der optimale (normierte) Verschiebungsfaktor | |
| − | |||
| − | + | ::<math>\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_1)}{ {\rm Pr}( m_0)} = 2 \cdot | |
| + | \frac{ E}{16 \cdot E} \cdot {\rm ln} \hspace{0.15cm} \frac{1/4}{3/4 } \approx - 0.14 | ||
| + | \hspace{0.05cm}.</math> | ||
| + | *Verschiebung nach links um $14\%$ hin zum unwahrscheinlicheren Symbol $\boldsymbol {s}_1$. Dadurch wird die Fehlerwahrscheinlichkeit geringfügig kleiner als bei gleichwahrscheinlichen Symbolen: | ||
| − | :<math>{\rm Pr}({ \cal E} ) = | + | ::<math>{\rm Pr}({ \cal E} )= 0.75 \cdot {\rm Q} \left ( 2 \cdot 1.14 \right ) + 0.25 \cdot {\rm Q} \left ( 2 \cdot 0.86 \right ) = 0.75 \cdot 0.0113 + 0.25 \cdot 0.0427 \approx 1.92\% \hspace{0.05cm}.</math> |
| − | + | Man erkennt aus diesen Zahlenwerten: | |
| + | #Durch die Schwellenverschiebung wird nun zwar das Symbol $\boldsymbol {s}_1$ stärker verfälscht, das wahrscheinlichere Symbol $\boldsymbol {s}_0$ jedoch überproportional weniger.<br> | ||
| + | #Das Ergebnis sollte aber nicht zu Fehlinterpretationen führen. Im unsymmetrischen Fall ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ ergibt sich zwar eine kleinere Fehlerwahrscheinlichkeit als für ${\rm Pr}( m_0) ={\rm Pr}( m_1) = 0.5$, aber mit jedem Symbol kann dann auch nur weniger Information übertragen werden. | ||
| + | # Bei den gewählten Zahlenwerten $0.81 \ \rm bit/Symbol$ statt $1\ \rm bit/Symbol$. Aus informationstheoretischer Sicht wäre ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ optimal.}} | ||
| − | |||
| − | == | + | {{BlaueBox|TEXT= |
| + | $\text{Fazit:}$ | ||
| + | *Im symmetrischen Fall ⇒ ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ können zur Entscheidungsfindung die herkömmlichen bedingten WDF–Werte $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$ herangezogen werden. | ||
| + | *Im unsymmetrischen Fall ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ müssen diese Funktionen vorher gewichtet werden: ${\rm Pr}(m_i) \cdot p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m_i } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$. | ||
| + | |||
| + | |||
| + | Im Folgenden wird dieser Sachverhalt berücksichtigt.}} | ||
| + | |||
| + | == Entscheidungsregionen im nichtbinären Fall == | ||
<br> | <br> | ||
| + | Allgemein partitionieren die Entscheidungsregionen $I_i$ den $N$–dimensionalen reellen Raum in $M$ zueinander disjunkte Gebiete. $I_i$ ist dabei definiert als die Menge aller Punkte, die zum Schätzwert $m_i$ führen: | ||
| − | {{ | + | ::<math>\boldsymbol{ \rho } \in I_i \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} \hat{m} = m_i, \hspace{0.3cm}{\rm wobei}\hspace{0.3cm}I_i = \left \{ \boldsymbol{ \rho } \in { \cal R}^N \hspace{0.05cm} | \hspace{0.05cm} |
| + | {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm} m_i ) > | ||
| + | {\rm Pr}( m_k) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm}m_k )\hspace{0.15cm} \forall k \ne i | ||
| + | \right \} \hspace{0.05cm}.</math> | ||
| − | + | *Die Form der Entscheidungsregionen $I_i$ mit $i = 0$, ... , $M-1$ im $N$–dimensionalen Raum hängen von den bedingten Wahrscheinlichkeitsdichtefunktionen $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m }$ ab, also vom betrachteten Kanal. | |
| + | |||
| + | *In vielen Fällen – so auch beim AWGN–Kanal – sind die Entscheidungsgrenzen zwischen je zwei Signalpunkten Gerade, was die weiteren Betrachtungen vereinfacht.<br> | ||
| − | |||
| − | Die | + | {{GraueBox|TEXT= |
| + | [[Datei:P ID2025 Dig T 4 3 S4 version2.png|right|frame|AWGN–Entscheidungsregionen für <br>$N = 2$, $M = 3$]] | ||
| + | $\text{Beispiel 3:}$ Die Grafik zeigt die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ für ein Übertragungssystem mit den Parametern $N = 2$ und $M = 3$. Die normierten Sendevektoren sind dabei | ||
| + | :$$\boldsymbol{ s }_0 = (2,\hspace{0.05cm} 2),$$ | ||
| + | :$$ \boldsymbol{ s }_1 = (1,\hspace{0.05cm} 3),$$ | ||
| + | :$$ \boldsymbol{ s }_2 = (1,\hspace{0.05cm} -1) \hspace{0.05cm}.$$ | ||
| − | : | + | Es sind nun zwei Fälle zu unterscheiden: |
| − | + | *Bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1) ={\rm Pr}( m_2) = 1/3 $ verlaufen die Grenzen zwischen jeweils zwei Regionen stets geradlinig, mittig und rechtwinklig zu den Verbindungsgeraden.<br> | |
| − | |||
| − | + | *Bei ungleichen Symbolwahrscheinlichkeiten sind dagegen die Entscheidungsgrenzen jeweils in Richtung des unwahrscheinlicheren Symbols parallel zu verschieben – umso weiter, je größer die AWGN–Streuung $\sigma_n$ ist.}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Fehlerwahrscheinlichkeitsberechnung im nichtbinären Fall == | |
| + | <br> | ||
| + | Nachdem die Entscheidungsregionen $I_i$ festliegen, kann man die Symbolfehlerwahrscheinlichkeit des Gesamtsystems berechnen. Wir benutzen folgende Bezeichnungen, wobei wir aufgrund der Einschränkungen durch unseren Zeichensatz im Fließtext manchmal andere Namen als in Gleichungen verwenden müssen: | ||
| + | #Symbolfehlerwahrscheinlichkeit: ${\rm Pr}({ \cal E} ) = {\rm Pr(Symbolfehler)} \hspace{0.05cm},$ | ||
| + | #Wahrscheinlichkeit für eine korrekte Entscheidung: ${\rm Pr}({ \cal C} ) = 1 - {\rm Pr}({ \cal E} ) = {\rm Pr(korrekte \hspace{0.15cm} Entscheidung)} \hspace{0.05cm},$ | ||
| + | #Bedingte Wahrscheinlichkeit einer korrekten Entscheidung unter der Bedingung $m = m_i$: ${\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) \hspace{0.05cm}.$ | ||
| − | |||
| − | + | *Mit diesen Definitionen gilt für die Wahrscheinlichkeit einer korrekten Entscheidung: | |
| − | {{ | + | ::<math>{\rm Pr}({ \cal C} ) \hspace{-0.1cm} = \hspace{-0.1cm} \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot |
| + | \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } | ||
| + | \hspace{0.05cm}.</math> | ||
| − | + | *Für den AWGN–Kanal gilt dabei entsprechend dem Abschnitt [[Digitalsignalübertragung/Struktur_des_optimalen_Empfängers#N.E2.80.93dimensionales_Gau.C3.9Fsches_Rauschen| "N–dimensionales Gaußsches Rauschen"]]: | |
| − | |||
| − | |||
| − | :<math>\ | + | ::<math>{\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) = \frac{1}{(\sqrt{2\pi} \cdot \sigma_n)^N} \cdot |
| + | \int_{I_i} {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_i ||^2 \right ] \,{\rm d} \boldsymbol {\rho }\hspace{0.05cm}.</math> | ||
| − | + | #Dieses Integral muss im allgemeinen Fall numerisch berechnet werden. | |
| − | + | #Nur bei einigen wenigen, einfach beschreibbaren Entscheidungsregionen $\{I_i\}$ ist eine analytische Lösung möglich.<br> | |
| − | |||
| − | |||
| − | |||
| − | {{Beispiel}} | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 4:}$ Beim AWGN–Kanal liegt eine 2D–Gaußglocke um den Sendepunkt $\boldsymbol{ s }_i$, in der linken Grafik erkennbar an den konzentrischen Höhenlinien. | ||
| + | [[Datei:P ID2026 Dig T 4 3 S5b version1.png|right|frame|Zur Berechnung der Fehlerwahrscheinlichkeit bei AWGN|class=fit]] | ||
| − | + | #Etwas willkürlich ist zudem die Entscheidungsgerade $G$ eingezeichnet. | |
| + | #Rechts dargestellt ist in einem anderen Koordinatensystem (verschoben und gedreht) allein die WDF des Rauschens. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Die Grafik kann wie folgt interpretiert werden: | |
| − | * | + | *Die Wahrscheinlichkeit, dass der Empfangsvektor nicht in das „Sollgebiet” $I_i$ fällt, sondern in das rot hinterlegte Gebiet $I_k$, ist $ {\rm Q} (A/\sigma_n)$. ${\rm Q}(x)$ ist die Gaußsche Fehlerfunktion. |
| − | + | ||
| + | *$A$ bezeichnet den Abstand zwischen $\boldsymbol{ s }_i$ und $G$. $\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an. | ||
| − | + | *Entsprechend ist die Wahrscheinlichkeit für das Ereignis $r \in I_i$ gleich dem Komplementärwert | |
| − | + | ::<math>{\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) = {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) = | |
| + | 1 - {\rm Q} (A/\sigma_n)\hspace{0.05cm}.</math>}}<br> | ||
| − | + | Wir betrachten nun die oben angegebenen Gleichungen, | |
| − | |||
| − | |||
| − | + | ::<math>{\rm Pr}({ \cal C} ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.3cm}{\rm mit} | |
| − | ::<math>{\rm Pr}({ \cal C} ) = 1 | + | \hspace{0.3cm} {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = |
| + | \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } | ||
| + | \hspace{0.05cm},</math> | ||
| − | + | etwas genauer, wobei wir wieder von zwei Basisfunktionen $(N = 2)$ und den drei Signalraumpunkten $\boldsymbol{ s }_0$, $\boldsymbol{ s }_1$ und $\boldsymbol{ s }_2$ $(M = 3)$ ausgehen. | |
| − | : | + | [[Datei:P ID2028 Dig T 4 3 S5 version1.png|right|frame|Fehlerwahrscheinlichkeitsberechnung beim AWGN-Kanal und $M = 3$]] |
| + | #Die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ sind [[Digitalsignalübertragung/Approximation_der_Fehlerwahrscheinlichkeit#Optimale_Schwelle_bei_nicht_gleichwahrscheinlichen_Symbolen|"bestmöglich"]] gewählt. | ||
| + | #Das AWGN–Rauschen ist in der Skizze durch jeweils drei kreisförmige Höhenlinien angedeutet. | ||
| − | |||
| − | |||
| − | |||
| − | : | + | Man erkennt aus dieser Darstellung: |
| − | + | *Unter der Voraussetzung, dass $m = m_i \ \Leftrightarrow \ \boldsymbol{ s } = \boldsymbol{ s }_i$ gesendet wurde, wird nur dann eine richtige Entscheidung getroffen, wenn der Empfangswert $\boldsymbol{ r }$ in der Region $I_i$ liegt.<br> | |
| − | |||
| − | |||
| − | + | *Die Wahrscheinlichkeit ${\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist für $i = 2$ (weitaus) am größten ⇒ richtige Entscheidung. | |
| − | + | *${\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist deutlich kleiner. Nahezu vernachlässigbar ist ${\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm}m_2)$. | |
| − | |||
| − | + | *Die Verfälschungswahrscheinlichkeiten für $m = m_0$ bzw. $m = m_1$ lauten somit: | |
| − | {{ | + | ::<math>{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ),</math> |
| + | ::<math> {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) ={\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) | ||
| + | \hspace{0.05cm}.</math> | ||
| − | + | *Die größte Verfälschungswahrscheinlichkeit ergibt sich für $m = m_0$. Wegen | |
| − | + | ::<math>{\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \approx {\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) | |
| − | + | \hspace{0.05cm}, </math> | |
| + | ::<math>{\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \gg {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) | ||
| + | \hspace{0.05cm}</math> | ||
| − | + | :gelten folgende Relationen: | |
| + | :$${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) > {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) >{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\hspace{0.05cm}. $$ | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Fazit:}$ Diese Ergebnisse können wie folgt zusammengefasst werden: | |
| − | + | #Zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit muss auch bei gleichwahrscheinlichen Symbolen allgemein über alle $M$ Terme gemittelt werden. | |
| + | #Bei gleichwahrscheinlichen Symbolen kann ${\rm Pr}(m_i) = 1/M$ vor die Summation gezogen werden, was allerdings den Rechengang nicht sonderlich vereinfacht. | ||
| + | #Nur bei symmetrischer Anordnung kann auf die Mittelung ganz verzichtet werden.<br>}} | ||
| − | == | + | == Union Bound - Obere Schranke für die Fehlerwahrscheinlichkeit== |
<br> | <br> | ||
| − | + | Bei beliebigen Werten von $M$ gilt für die Verfälschungswahrscheinlichkeit unter der Voraussetzung, dass die Nachricht $m_i$ $($bzw. das Signal $\boldsymbol{s}_i)$ gesendet wurde: | |
| + | |||
| + | ::<math>{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] | ||
| + | \hspace{0.05cm},\hspace{0.5cm}{ \cal E}_{ik}\hspace{-0.1cm}: \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i | ||
| + | \hspace{0.05cm}. </math> | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ Für diesen Ausdruck lässt sich mit einer Booleschen Ungleichung – der so genannten '''Union Bound''' – eine obere Schranke angeben: | ||
| + | |||
| + | ::<math>{\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) \le \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1} | ||
| + | {\rm Pr}({ \cal E}_{ik}) = \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ]\hspace{0.05cm}. </math> | ||
| + | |||
| + | <u>Anmerkungen:</u> | ||
| + | #$d_{ik} = \vert \hspace{-0.05cm} \vert \boldsymbol{s}_i - \boldsymbol{s}_k \vert \hspace{-0.05cm} \vert$ ist der Abstand der Signalraumpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$. | ||
| + | #$\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an.<br> | ||
| + | #Die "Union Bound" ist nur bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(m_i) = 1/M$ anwendbar. | ||
| + | #Auch dann muss zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit über alle $m_i$ gemittelt werden.}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel 5:}$ Die Grafik verdeutlicht die <b>Union Bound</b> am Beispiel $M = 3$ mit gleichwahrscheinlichen Symbolen: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) =1/3$.<br> | |
| − | [[Datei:P | + | [[Datei:P ID2041 Dig T 4 3 S6 version1.png|right|frame|Zur Verdeutlichung der „Union Bound”|class=fit]] |
| + | Zu diesen Darstellungen ist anzumerken: | ||
| + | :$${\rm Pr}({ \cal E} ) = 1 - {\rm Pr}({ \cal C} ) \hspace{0.05cm},$$ | ||
| + | :$${\rm Pr}({ \cal C} ) = {1}/{3} \cdot | ||
| + | \big [ {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_1 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_2 ) \big ]\hspace{0.05cm}.$$ | ||
| − | + | *Der erste Term ${\rm Pr}(\boldsymbol{r} \in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ im Klammerausdruck unter der Voraussetzung $m = m_0 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_0$ ist in der linken Grafik durch die rote Region $I_0$ visualisiert. | |
| − | * | ||
| − | *Die | + | *Die Komplementärregion ${\rm Pr}(\boldsymbol{r} \not\in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ ist links entweder blau oder grün oder blau–grün schraffiert markiert. Es gilt ${\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = 1 - {\rm Pr}({ \cal E}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 )$ mit |
| + | :$${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = | ||
| + | {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\cup \hspace{0.05cm} \boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) + | ||
| + | {\rm Pr}(\boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) $$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Q} \big [ d_{01}/(2{\sigma_n}) \big ]+ | ||
| + | {\rm Q} \big [ d_{02}/(2{\sigma_n}) \big ] | ||
| + | \hspace{0.05cm}.$$ | ||
| − | *Die | + | *Das „$\le$”–Zeichen berücksichtigt hier, dass die blau–grün schraffierte Fläche sowohl zum Gebiet „$\boldsymbol{r} \in I_1$” als auch zum Gebiet „$\boldsymbol{r} \in I_2$” gehört, so dass die Summe einen zu großen Wert liefert. Das heißt: Die Union Bound liefert stets eine obere Schranke.<br> |
| − | + | *Die mittlere Grafik verdeutlicht die Berechnung der Union Bound unter der Voraussetzung, dass $m = m_1 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_1$ gesendet wurde. | |
| − | + | ||
| − | + | *Dem rechten Bild liegt $m = m_2 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_2$ zugrunde.}}<br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | + | == Weitere Aufwandsreduzierung bei der Union Bound== |
| + | <br> | ||
| + | Die Abschätzung nach der „Union Bound” lässt sich weiter verbessern, indem man nur solche Signalraumpunkte berücksichtigt, die direkte Nachbarn des aktuellen Sendevektors $\boldsymbol{s}_i$ sind: | ||
| + | [[Datei:P ID2032 Dig T 4 3 S6b version1.png|right|frame|Zur Definition der Nachbarmengen $N(i)$]] | ||
| − | ::<math>{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} | + | ::<math>{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}{\rm Q}\big [ d_{ik}/(2{\sigma_n}) \big ] |
| + | \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \hspace{0.05cm}\in \hspace{0.05cm}N(i)}^{M-1}\hspace{-0.4cm}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ] | ||
| + | \hspace{0.05cm}. </math> | ||
| − | + | Dazu definieren wir die Nachbarn von $\boldsymbol{s}_i$ als | |
| − | |||
| − | + | ::<math>N(i) = \left \{ k \in \left \{ i = 0, 1, 2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, M-1 \right \}\hspace{0.05cm}|\hspace{0.05cm} I_i {\rm \hspace{0.15cm}grenzt \hspace{0.15cm}direkt \hspace{0.15cm}an \hspace{0.15cm}}I_k \right \} | |
| + | \hspace{0.05cm}. </math> | ||
| + | Die Grafik verdeutlicht diese Definiton am Beispiel $M = 5$. | ||
| + | *Die Regionen $I_0$ und $I_3$ haben jeweils nur zwei direkte Nachbarn, | ||
| + | *während $I_4$ an alle anderen Entscheidungsregionen angrenzt. | ||
| + | Durch die Einführung der Nachbarmengen $N(i)$ wird die Qualität der Union Bound–Approximation verbessert, das heißt, die Schranke liegt dann näher an der tatsächlichen Fehlerwahrscheinlichkeit, wird also nach unten verschoben. | ||
| + | Eine weitere Schranke benutzt nur den minimalen Abstand $d_{\rm min}$ zwischen zwei Signalraumpunkten: | ||
| + | *Im obigen Beispiel tritt dieser zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ auf. | ||
| + | *Für gleichwahrscheinliche Symbole ⇒ ${\rm Pr}(m_i) =1/M$ gilt dann die folgende Abschätzung: | ||
| + | ::<math>{\rm Pr}({ \cal E} ) \le \sum\limits_{i = 0 }^{M-1} \left [ {\rm Pr}(m_i) \cdot \sum\limits_{k \ne i }{\rm Q} \big [d_{ik}/(2{\sigma_n})\big ] \right ] | ||
| + | \le \frac{1}{M} \cdot \sum\limits_{i = 0 }^{M-1} \left [ \sum\limits_{k \ne i } {\rm Q} [d_{\rm min}/(2{\sigma_n})] \right ] = \sum\limits_{k \ne i }{\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] = (M-1) \cdot | ||
| + | {\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] | ||
| + | \hspace{0.05cm}. </math> | ||
| + | Hierzu ist anzumerken: | ||
| + | #Diese Schranke ist auch für große $M$ sehr einfach zu berechnen. Bei vielen Anwendungen ergibt sich jedoch damit eine viel zu große Fehlerwahrscheinlichkeit.<br> | ||
| + | #Die Schranke ist nur dann gleich der tatsächlichen Fehlerwahrscheinlichkeit, wenn die Distanzen aller $M$ Signalpunkte zueinander gleich $d_{\rm min}$ sind.<br> | ||
| + | #Im Sonderfall $M = 2$ ist diese Voraussetzung häufig erfüllt, so dass die Schranke exakt mit der tatsächlichen Fehlerwahrscheinlichkeit übereinstimmt.<br> | ||
| + | == Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:4.06_Optimale_Entscheidungsgrenzen|Aufgabe 4.6: Optimale Entscheidungsgrenze]] | ||
| + | [[Aufgaben:4.06Z_Signalraumkonstellationen|Aufgabe 4.6Z: Signalraumkonstellationen]] | ||
| + | [[Aufgaben:Aufgabe_4.07:_Nochmals_Entscheidungsgrenzen|Aufgabe 4.7: Nochmals Entscheidungsgrenzen]] | ||
| + | [[Aufgaben:4.08_Entscheidungsregionen_bei_drei_Symbolen|Aufgabe 4.8: Entscheidungsregionen bei drei Symbolen]] | ||
| + | [[Aufgaben:4.08Z_Fehlerwahrscheinlichkeit_bei_drei_Symbolen|Aufgabe 4.8Z: Fehlerwahrscheinlichkeit bei drei Symbolen]] | ||
| + | [[Aufgaben:Aufgabe_4.09:_Entscheidungsregionen_bei_Laplace|Aufgabe 4.9: Entscheidungsregionen bei Laplace]] | ||
| + | [[Aufgaben:Aufgabe_4.09Z:_Laplace-verteiltes_Rauschen|Aufgabe 4.9Z: Laplace-verteiltes Rauschen]] | ||
| + | [[Aufgaben:4.10_Union_Bound|Aufgabe 4.10: Union Bound]] | ||
{{Display}} | {{Display}} | ||
Aktuelle Version vom 27. Juli 2022, 15:24 Uhr
Inhaltsverzeichnis
- 1 Optimale Entscheidung bei binärer Übertragung
- 2 Der Sonderfall gleichwahrscheinlicher Binärsymbolen
- 3 Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen
- 4 Optimale Schwelle bei nicht gleichwahrscheinlichen Symbolen
- 5 Entscheidungsregionen im nichtbinären Fall
- 6 Fehlerwahrscheinlichkeitsberechnung im nichtbinären Fall
- 7 Union Bound - Obere Schranke für die Fehlerwahrscheinlichkeit
- 8 Weitere Aufwandsreduzierung bei der Union Bound
- 9 Aufgaben zum Kapitel
Optimale Entscheidung bei binärer Übertragung
Wir gehen hier von einem Übertragungssystem aus, das wie folgt charakterisiert werden kann: $\boldsymbol{r} = \boldsymbol{s} + \boldsymbol{n}$. Dieses System weist folgende Eigenschaften auf:
- Der das Übertragungssystem vollständig beschreibende Vektorraum wird von $N = 2$ zueinander orthogonalen Basisfunktionen $\varphi_1(t)$ und $\varphi_2(t)$ aufgespannt.
- Demzufolge ist auch die Wahrscheinlichkeitsdichtefunktion des additiven und weißen Gaußschen Rauschens zweidimensional anzusetzen, gekennzeichnet durch den Vektor $\boldsymbol{ n} = (n_1,\hspace{0.05cm}n_2)$.
- Es gibt nur zwei mögliche Sendesignale $(M = 2)$, die durch die beiden Vektoren $\boldsymbol{ s_0} = (s_{01},\hspace{0.05cm}s_{02})$ und $\boldsymbol{ s_1} = (s_{11},\hspace{0.05cm}s_{12})$ beschrieben werden:
- $$s_0(t)= s_{01} \cdot \varphi_1(t) + s_{02} \cdot \varphi_2(t) \hspace{0.05cm},$$
- $$s_1(t) = s_{11} \cdot \varphi_1(t) + s_{12} \cdot \varphi_2(t) \hspace{0.05cm}.$$
- Die beiden Nachrichten $m_0 \ \Leftrightarrow \ \boldsymbol{ s_0}$ und $m_1 \ \Leftrightarrow \ \boldsymbol{ s_1}$ sind nicht notwendigermaßen gleichwahrscheinlich.
- Aufgabe des Entscheiders ist es, einen Schätzwert für den Empfangsvektor $\boldsymbol{r}$ nach der "MAP–Entscheidungsregel" anzugeben. Diese lautet im vorliegenden Fall mit $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2) \hspace{0.05cm}$:
- $$\hat{m} = {\rm arg} \max_i \hspace{0.1cm} \big[ {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm}|\hspace{0.05cm} m_i )\big ] \hspace{0.15cm} \in \hspace{0.15cm}\{ m_i\} \hspace{0.05cm}.$$
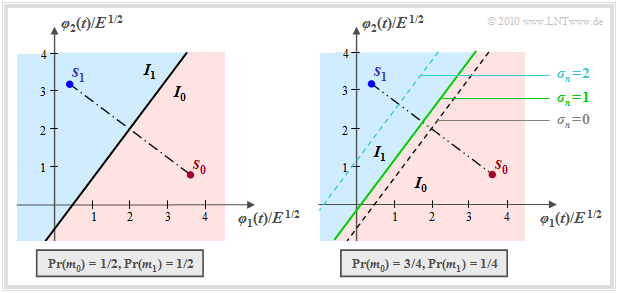
- Im betrachteten Sonderfall $N = 2$ und $M = 2$ partitioniert der Entscheider den zweidimensionalen Raum in die zwei disjunkten Gebiete $I_0$ (rot hinterlegt) und $I_1$ (blau), wie die nebenstehende Grafik verdeutlicht.
- Liegt der Empfangswert in $I_0$, so wird als Schätzwert $m_0$ ausgegeben, andernfalls $m_1$.
$\text{Herleitung und Bildbeschreibung:}$ Beim AWGN–Kanal und $M = 2$ lautet somit die Entscheidungsregel:
⇒ Man entscheide sich immer dann für die Nachricht $m_0$, falls folgende Bedingung erfüllt ist:
- $${\rm Pr}( m_0) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 \right ] > {\rm Pr}( m_1) \cdot {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 \right ] \hspace{0.05cm}.$$
⇒ Die Grenzlinie zwischen den beiden Entscheidungsregionen $I_0$ und $I_1$ erhält man, wenn man in obiger Gleichung das Größerzeichen durch das Gleichheitszeichen ersetzt und die Gleichung etwas umformt:
- $$\vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_0)\big ] = \vert \hspace{-0.05cm} \vert \boldsymbol{ \rho } - \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm}\big [{\rm Pr}( m_1)\big ]$$
- $$\Rightarrow \hspace{0.3cm} \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert^2 + 2 \sigma_n^2 \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_0)}{ {\rm Pr}( m_1)} = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
Aus dieser Darstellung erkennt man:
- Die Grenzkurve zwischen den Regionen $I_0$ und $I_1$ ist eine Gerade, da die Bestimmungsgleichung linear im Empfangsvektor $\boldsymbol{ \rho } = (\rho_1, \hspace{0.05cm}\rho_2)$ ist.
- Bei gleichwahrscheinlichen Symbolen verläuft die Grenze genau in der Mitte zwischen $\boldsymbol{ s }_0$ und $\boldsymbol{ s }_1$ und um $90^\circ$ verdreht gegenüber der Verbindungslinie zwischen diesen Sendepunkten (linke Grafik):
- $$\vert \hspace{-0.05cm} \vert \boldsymbol{ s }_1 \vert \hspace{-0.05cm} \vert ^2 - \vert \hspace{-0.05cm} \vert \boldsymbol{ s }_0 \vert \hspace{-0.05cm} \vert ^2 = 2 \cdot \boldsymbol{ \rho }^{\rm T} \cdot (\boldsymbol{ s }_1 - \boldsymbol{ s }_0)\hspace{0.05cm}.$$
- Für ${\rm Pr}(m_0) > {\rm Pr}(m_1)$ ist die Entscheidungsgrenze in Richtung des unwahrscheinlicheren Symbols $\boldsymbol{ s }_1$ verschoben, und zwar um so mehr, je größer die AWGN–Streuung $\sigma_n$ ist.
- Die grün–durchgezogene Entscheidungsgrenze im rechten Bild sowie die Entscheidungsregionen $I_0$ (rot) und $I_1$ (blau) gelten für die (normierte) Streuung $\sigma_n = 1$ und die gestrichelten Grenzlinien für $\sigma_n = 0$ bzw. $\sigma_n = 2$.
Der Sonderfall gleichwahrscheinlicher Binärsymbolen
Wir gehen weiterhin von einem Binärsystem aus $(M = 2)$, betrachten aber nun den einfachen Fall, dass dieses durch eine einzige Basisfunktion beschrieben werden kann $(N = 1)$. Die Fehlerwahrscheinlichkeit hierfür wurde bereits im Abschnitt "Definition der Bitfehlerwahrscheinlichkeit" berechnet.
Mit der für das vierte Hauptkapitel gewählten Nomenklatur und Darstellungsform ergibt sich folgende Konstellation:
- Der Empfangswert $r = s + n$ ist nunmehr ein Skalar und setzt sich aus dem Sendesignal $s \in \{s_0, \hspace{0.05cm}s_1\}$ und dem Rauschterm $n$ additiv zusammen. Die Abszisse $\rho$ bezeichnet eine Realisierung von $r$.
- Die Abszisse ist zudem auf die Bezugsgröße $\sqrt{E}$ normiert, wobei die formale Normierungsenergie $E$ keine physikalisch interpretierbare Bedeutung hat.
- Der Rauschterm $n$ ist gaußverteilt mit Mittelwert $m_n = 0$ und Varianz $\sigma_n^2$. Die Wurzel aus der Varianz $(\sigma_n)$ wird als der Effektivwert oder die Streuung bezeichnet.
- Die Entscheidergrenze $G$ unterteilt den gesamten Wertebereich von $r$ in die zwei Teilbereiche $I_0$ $($in dem unter anderem $s_0$ liegt$)$ und $I_1$ $($mit dem Signalwert $s_1)$.
- Ist $\rho > G$, so liefert der Entscheider den Schätzwert $m_0$, andernfalls $m_1$. Hierbei ist vorausgesetzt, dass die Nachricht $m_i$ mit dem Sendesignal $s_i$ eineindeutig zusammenhängt: $m_i \Leftrightarrow s_i$.
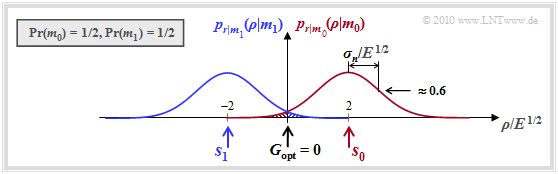
Die Grafik zeigt die bedingten (eindimensionalen) Wahrscheinlichkeitsdichtefunktionen $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_0}$ und $p_{\hspace{0.02cm}r\hspace{0.05cm} \vert \hspace{0.05cm}m_1}$ für den AWGN–Kanal, wobei gleiche Symbolwahrscheinlichkeiten vorausgesetzt sind: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Die (optimale) Entscheidergrenze ist somit $G = 0$. Man erkennt aus dieser Darstellung:
- Ist $m = m_0$ ⇒ t $s = s_0 = 2 \cdot E^{1/2}$, so kommt es nur dann zu einer Fehlentscheidung, wenn $\eta$, die Realisierung der Rauschgröße $n$, kleiner ist als $-2 \cdot E^{1/2}$.
- In diesem Fall ist $\rho < 0$, wobei $\rho$ eine Realisierung des Empfangswertes $r$ bezeichnet.
- Bei $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$ kommt es dagegen immer dann zu einer Fehlentscheidung, wenn $\eta$ größer ist als $+2 \cdot E^{1/2}$. In diesem Fall ist $\rho > 0$.
Fehlerwahrscheinlichkeit bei gleichwahrscheinlichen Symbolen
Es gelte ${\rm Pr}(m_0) = {\rm Pr}(m_1) = 0.5$. Bei AWGN–Rauschen mit Effektivwert (Streuung) $\sigma_n$ erhält man, wie bereits im Abschnitt "Definition der Bitfehlerwahrscheinlichkeit" mit anderer Nomenklatur berechnet wurde, für die Wahrscheinlichkeit einer Fehlentscheidung $(\cal E)$ unter der Bedingung, dass die Nachricht $m_0$ gesendet wurde:
- $${\rm Pr}({ \cal E}\hspace{0.05cm} \vert \hspace{0.05cm} m_0) = \int_{-\infty}^{G = 0} p_{r \hspace{0.05cm}|\hspace{0.05cm}m_0 } ({ \rho } \hspace{0.05cm} \vert \hspace{0.05cm}m_0 ) \,{\rm d} \rho = \int_{-\infty}^{- s_0 } p_{{ n} \hspace{0.05cm}\vert\hspace{0.05cm}m_0 } ({ \eta } \hspace{0.05cm}|\hspace{0.05cm}m_0 ) \,{\rm d} \eta = \int_{-\infty}^{- s_0 } p_{{ n} } ({ \eta } ) \,{\rm d} \eta = \int_{ s_0 }^{\infty} p_{{ n} } ({ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {s_0 }/{\sigma_n} \right ) \hspace{0.05cm}.$$
Bei der Herleitung der Gleichung wurde berücksichtigt, dass das AWGN–Rauschen $\eta$ unabhängig vom Signal $(m_0$ oder $m_1)$ ist und eine symmetrische WDF besitzt. Verwendet wurde zudem das komplementäre Gaußsche Fehlerintegral
- $${\rm Q}(x) = \frac{1}{\sqrt{2\pi}} \int_{x}^{\infty} {\rm e}^{-u^2/2} \,{\rm d} u \hspace{0.05cm}.$$
Entsprechend gilt für $m = m_1$ ⇒ $s = s_1 = -2 \cdot E^{1/2}$:
- $${\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = \int_{0}^{\infty} p_{{ r} \hspace{0.05cm}\vert\hspace{0.05cm}m_1 } ({ \rho } \hspace{0.05cm}\vert\hspace{0.05cm}m_1 ) \,{\rm d} \rho = \int_{- s_1 }^{\infty} p_{{ n} } (\boldsymbol{ \eta } ) \,{\rm d} \eta = {\rm Q} \left ( {- s_1 }/{\sigma_n} \right ) \hspace{0.05cm}.$$
$\text{Fazit:}$ Mit dem Abstand $d = s_1 - s_0$ der Signalraumpunkte kann man die Ergebnisse zusammenfassen, wobei noch ${\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$ zu berücksichtigen ist:
- $${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0) = {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1) = {\rm Q} \big ( {d}/(2{\sigma_n}) \big )$$
- $$\Rightarrow \hspace{0.3cm}{\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_0) + {\rm Pr}(m_1) \cdot {\rm Pr}({ \cal E} \hspace{0.05cm}\vert\hspace{0.05cm} m_1)= \big [ {\rm Pr}(m_0) + {\rm Pr}(m_1) \big ] \cdot {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] \hspace{0.05cm}.$$
Hinweise:
- Diese Gleichung gilt unter der Voraussetzung $G = 0$ ganz allgemein, also auch für ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$.
- Bei "nicht gleichwahrscheinlichen Symbolen" lässt sich allerdings die Fehlerwahrscheinlichkeit durch eine andere Entscheidergrenze verkleinern.
- Die hier genannte Gleichung gilt auch dann, wenn die Signalraumpunkte keine Skalare sind, sondern durch die Vektoren $\boldsymbol{ s}_0$ und $\boldsymbol{ s}_1$ beschrieben werden.
- Der Abstand $d$ ergibt sich dann als die "Norm" des Differenzvektors: $d = \vert \hspace{-0.05cm} \vert \hspace{0.05cm} \boldsymbol{ s}_1 - \boldsymbol{ s}_0 \hspace{0.05cm} \vert \hspace{-0.05cm} \vert \hspace{0.05cm}.$
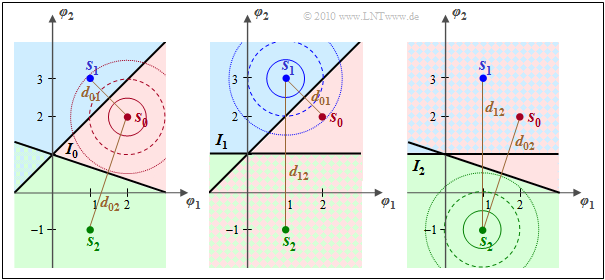
$\text{Beispiel 1:}$ Betrachten wir nochmals die Signalraumkonstellation von der ersten Kapitelseite (untere Grafik) mit den Werten
- $\boldsymbol{ s}_0/E^{1/2} = (3.6, \hspace{0.05cm}0.8)$,
- $\boldsymbol{ s}_1/E^{1/2} = (0.4, \hspace{0.05cm}3.2)$.
Hier beträgt der Abstand der Signalraumpunkte
- $$d = \vert \hspace{-0.05cm} \vert s_1 - s_0 \vert \hspace{-0.05cm} \vert = \sqrt{E \cdot (0.4 - 3.6)^2 + E \cdot (3.2 - 0.8)^2} = 4 \cdot \sqrt {E}\hspace{0.05cm}.$$
Es ergibt sich also der genau gleiche Wert wie für die obere Konstellation mit
- $\boldsymbol{ s}_0/E^{1/2} = (2, \hspace{0.05cm}0)$,
- $\boldsymbol{ s}_1/E^{1/2} = (-2, \hspace{0.05cm}0)$.
Die Abbildungen zeigen diese beiden Konstellationen und lassen folgende Gemeinsamkeiten bzw. Unterschiede erkennen, wobei jeweils von der AWGN–Rauschvarianz $\sigma_n^2 = N_0/2$ ausgegangen wird. Die Kreise in der Grafik veranschaulichen die zirkuläre Symmetrie von 2D–AWGN–Rauschen.
- Wie bereits gesagt, sind sowohl der Abstand der Signalpunkte von der Entscheidungsgeraden $(d/2 = 2 \cdot \sqrt {E})$ als auch der AWGN–Kennwert $\sigma_n$ in beiden Fällen gleich.
- Daraus folgt: Die beiden Anordnungen führen zur gleichen Fehlerwahrscheinlichkeit, wenn man den Parameter $E$ (eine Art Normierungsenergie) konstant lässt:
- $${\rm Pr} ({\rm Symbolfehler}) = {\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ]\hspace{0.05cm}.$$
- Die "mittlere Energie pro Symbol" ⇒ $E_{\rm S}$ ergibt sich für die obere Konstellation zu
- $$E_{\rm S} = 1/2 \cdot \vert \hspace{-0.05cm} \vert s_0 \vert \hspace{-0.05cm} \vert^2 + 1/2 \cdot \vert \hspace{-0.05cm} \vert s_1 \vert \hspace{-0.05cm} \vert^2 = E/2 \cdot \big[(+2)^2 + (-2)^2\big] = 4 \cdot {E}\hspace{0.05cm}.$$
- Bei der unteren Konstellation erhält man in gleicher Weise:
- $$E_{\rm S} = \ \text{...} \ = E/2 \cdot \big[(3.6)^2 + (0.8)^2\big] + E/2 \cdot \big[(0.4)^2 + (3.2)^2 \big] = 12 \cdot {E}\hspace{0.05cm}.$$
- Bei gegebener mittlerer Energie pro Symbol $(E_{\rm S})$ ist demnach die obere Konstellation der unteren deutlich überlegen: Die gleiche Fehlerwahrscheinlichkeit ergibt sich mit einem Drittel der aufzuwendenden Energie pro Symbol. Auf diesen Sachverhalt wird in der "Aufgabe 4.6Z" noch im Detail eingegangen.
Optimale Schwelle bei nicht gleichwahrscheinlichen Symbolen
Gilt ${\rm Pr}(m_0) \ne {\rm Pr}(m_1)$, so kann man durch eine Verschiebung der Entscheidungsgrenze $G$ eine etwas kleinere Fehlerwahrscheinlichkeit erreichen. Die nachfolgenden Ergebnisse werden ausführlich in der Musterlösung zur "Aufgabe 4.7" hergeleitet:
- Bei ungleichen Symbolwahrscheinlichkeiten liegt die optimale Entscheidungsgrenze $G_{\rm opt}$ zwischen den Regionen $I_0$, $I_1$ näher beim unwahrscheinlicheren Symbol.
- Die normierte optimale Verschiebung gegenüber der Grenze $G = 0$ bei gleichwahrscheinlichen Symbolen beträgt
- \[\gamma_{\rm opt} = \frac{G_{\rm opt}}{s_0 } = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm}.\]
- Die Fehlerwahrscheinlichkeit ist dann gleich
- $${\rm Pr}({ \cal E} ) = {\rm Pr}(m_0) \cdot {\rm Q} \big[ {d}/(2{\sigma_n}) \cdot (1 - \gamma_{\rm opt}) \big ] + {\rm Pr}(m_1) \cdot {\rm Q} \big [ {d}/(2{\sigma_n}) \cdot (1 + \gamma_{\rm opt}) \big ]\hspace{0.05cm}.$$
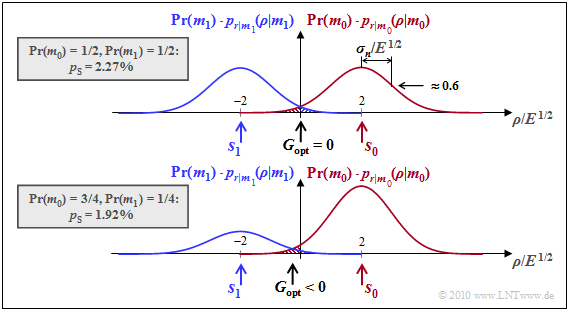
$\text{Beispiel 2:}$ Der formale Parameter $\rho$ (Abszisse) kennzeichnet wieder eine Realisierung der AWGN–Zufallsgröße $r = s + n$.
Für das Folgende gelte weiter:
- $$\boldsymbol{ s }_0 = (2 \cdot \sqrt{E}, \hspace{0.1cm} 0), \hspace{0.2cm} \boldsymbol{ s }_1 = (- 2 \cdot \sqrt{E}, \hspace{0.1cm} 0)$$
- $$ \Rightarrow \hspace{0.2cm} d = 2 \cdot \sqrt{E}, \hspace{0.2cm} \sigma_n = \sqrt{E} \hspace{0.05cm}.$$
- Bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1)$ ergibt sich die optimale Entscheidungsgrenze zu $G_{\rm opt} = 0$ (siehe obere Skizze). Damit erhält man für die Fehlerwahrscheinlichkeit:
- $${\rm Pr}({ \cal E} ) = {\rm Q} \big [ {d}/(2{\sigma_n}) \big ] = {\rm Q} (2) \approx 2.26\% \hspace{0.05cm}.$$
- Nun betrachten wir mit ${\rm Pr}( m_0) = 3/4\hspace{0.05cm},\hspace{0.1cm}{\rm Pr}( m_1) = 1/4\hspace{0.05cm}$ ungleiche Symbolwahrscheinlichkeiten (untere Skizze). Die weiteren Größen seien gegenüber der oberen Grafik unverändert. In diesem Fall beträgt der optimale (normierte) Verschiebungsfaktor
- \[\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}( m_1)}{ {\rm Pr}( m_0)} = 2 \cdot \frac{ E}{16 \cdot E} \cdot {\rm ln} \hspace{0.15cm} \frac{1/4}{3/4 } \approx - 0.14 \hspace{0.05cm}.\]
- Verschiebung nach links um $14\%$ hin zum unwahrscheinlicheren Symbol $\boldsymbol {s}_1$. Dadurch wird die Fehlerwahrscheinlichkeit geringfügig kleiner als bei gleichwahrscheinlichen Symbolen:
- \[{\rm Pr}({ \cal E} )= 0.75 \cdot {\rm Q} \left ( 2 \cdot 1.14 \right ) + 0.25 \cdot {\rm Q} \left ( 2 \cdot 0.86 \right ) = 0.75 \cdot 0.0113 + 0.25 \cdot 0.0427 \approx 1.92\% \hspace{0.05cm}.\]
Man erkennt aus diesen Zahlenwerten:
- Durch die Schwellenverschiebung wird nun zwar das Symbol $\boldsymbol {s}_1$ stärker verfälscht, das wahrscheinlichere Symbol $\boldsymbol {s}_0$ jedoch überproportional weniger.
- Das Ergebnis sollte aber nicht zu Fehlinterpretationen führen. Im unsymmetrischen Fall ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ ergibt sich zwar eine kleinere Fehlerwahrscheinlichkeit als für ${\rm Pr}( m_0) ={\rm Pr}( m_1) = 0.5$, aber mit jedem Symbol kann dann auch nur weniger Information übertragen werden.
- Bei den gewählten Zahlenwerten $0.81 \ \rm bit/Symbol$ statt $1\ \rm bit/Symbol$. Aus informationstheoretischer Sicht wäre ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ optimal.
$\text{Fazit:}$
- Im symmetrischen Fall ⇒ ${\rm Pr}( m_0) ={\rm Pr}( m_1)$ können zur Entscheidungsfindung die herkömmlichen bedingten WDF–Werte $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$ herangezogen werden.
- Im unsymmetrischen Fall ⇒ ${\rm Pr}( m_0) \ne {\rm Pr}( m_1)$ müssen diese Funktionen vorher gewichtet werden: ${\rm Pr}(m_i) \cdot p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m_i } ( \rho \hspace{0.05cm}\vert \hspace{0.05cm}m_i )$.
Im Folgenden wird dieser Sachverhalt berücksichtigt.
Entscheidungsregionen im nichtbinären Fall
Allgemein partitionieren die Entscheidungsregionen $I_i$ den $N$–dimensionalen reellen Raum in $M$ zueinander disjunkte Gebiete. $I_i$ ist dabei definiert als die Menge aller Punkte, die zum Schätzwert $m_i$ führen:
- \[\boldsymbol{ \rho } \in I_i \hspace{0.2cm} \Longleftrightarrow \hspace{0.2cm} \hat{m} = m_i, \hspace{0.3cm}{\rm wobei}\hspace{0.3cm}I_i = \left \{ \boldsymbol{ \rho } \in { \cal R}^N \hspace{0.05cm} | \hspace{0.05cm} {\rm Pr}( m_i) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm} m_i ) > {\rm Pr}( m_k) \cdot p_{\boldsymbol{ r} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol{ \rho } \hspace{0.05cm} | \hspace{0.05cm}m_k )\hspace{0.15cm} \forall k \ne i \right \} \hspace{0.05cm}.\]
- Die Form der Entscheidungsregionen $I_i$ mit $i = 0$, ... , $M-1$ im $N$–dimensionalen Raum hängen von den bedingten Wahrscheinlichkeitsdichtefunktionen $p_{r \hspace{0.05cm}\vert \hspace{0.05cm}m }$ ab, also vom betrachteten Kanal.
- In vielen Fällen – so auch beim AWGN–Kanal – sind die Entscheidungsgrenzen zwischen je zwei Signalpunkten Gerade, was die weiteren Betrachtungen vereinfacht.
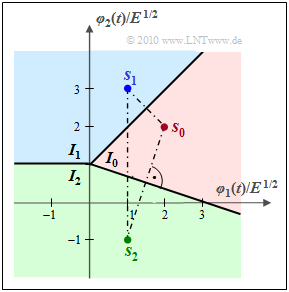
$\text{Beispiel 3:}$ Die Grafik zeigt die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ für ein Übertragungssystem mit den Parametern $N = 2$ und $M = 3$. Die normierten Sendevektoren sind dabei
- $$\boldsymbol{ s }_0 = (2,\hspace{0.05cm} 2),$$
- $$ \boldsymbol{ s }_1 = (1,\hspace{0.05cm} 3),$$
- $$ \boldsymbol{ s }_2 = (1,\hspace{0.05cm} -1) \hspace{0.05cm}.$$
Es sind nun zwei Fälle zu unterscheiden:
- Bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}( m_0) = {\rm Pr}( m_1) ={\rm Pr}( m_2) = 1/3 $ verlaufen die Grenzen zwischen jeweils zwei Regionen stets geradlinig, mittig und rechtwinklig zu den Verbindungsgeraden.
- Bei ungleichen Symbolwahrscheinlichkeiten sind dagegen die Entscheidungsgrenzen jeweils in Richtung des unwahrscheinlicheren Symbols parallel zu verschieben – umso weiter, je größer die AWGN–Streuung $\sigma_n$ ist.
Fehlerwahrscheinlichkeitsberechnung im nichtbinären Fall
Nachdem die Entscheidungsregionen $I_i$ festliegen, kann man die Symbolfehlerwahrscheinlichkeit des Gesamtsystems berechnen. Wir benutzen folgende Bezeichnungen, wobei wir aufgrund der Einschränkungen durch unseren Zeichensatz im Fließtext manchmal andere Namen als in Gleichungen verwenden müssen:
- Symbolfehlerwahrscheinlichkeit: ${\rm Pr}({ \cal E} ) = {\rm Pr(Symbolfehler)} \hspace{0.05cm},$
- Wahrscheinlichkeit für eine korrekte Entscheidung: ${\rm Pr}({ \cal C} ) = 1 - {\rm Pr}({ \cal E} ) = {\rm Pr(korrekte \hspace{0.15cm} Entscheidung)} \hspace{0.05cm},$
- Bedingte Wahrscheinlichkeit einer korrekten Entscheidung unter der Bedingung $m = m_i$: ${\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) \hspace{0.05cm}.$
- Mit diesen Definitionen gilt für die Wahrscheinlichkeit einer korrekten Entscheidung:
- \[{\rm Pr}({ \cal C} ) \hspace{-0.1cm} = \hspace{-0.1cm} \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm}.\]
- Für den AWGN–Kanal gilt dabei entsprechend dem Abschnitt "N–dimensionales Gaußsches Rauschen":
- \[{\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = 1 - {\rm Pr}({ \cal E} \hspace{0.05cm}|\hspace{0.05cm} m_i) = \frac{1}{(\sqrt{2\pi} \cdot \sigma_n)^N} \cdot \int_{I_i} {\rm exp} \left [ - \frac{1}{2 \sigma_n^2} \cdot || \boldsymbol{ \rho } - \boldsymbol{ s }_i ||^2 \right ] \,{\rm d} \boldsymbol {\rho }\hspace{0.05cm}.\]
- Dieses Integral muss im allgemeinen Fall numerisch berechnet werden.
- Nur bei einigen wenigen, einfach beschreibbaren Entscheidungsregionen $\{I_i\}$ ist eine analytische Lösung möglich.
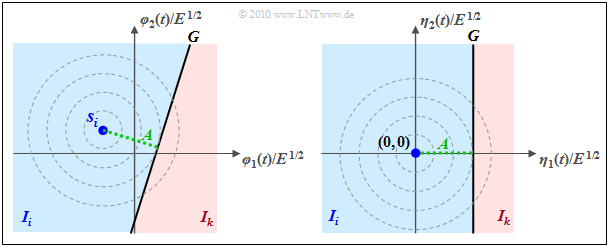
$\text{Beispiel 4:}$ Beim AWGN–Kanal liegt eine 2D–Gaußglocke um den Sendepunkt $\boldsymbol{ s }_i$, in der linken Grafik erkennbar an den konzentrischen Höhenlinien.
- Etwas willkürlich ist zudem die Entscheidungsgerade $G$ eingezeichnet.
- Rechts dargestellt ist in einem anderen Koordinatensystem (verschoben und gedreht) allein die WDF des Rauschens.
Die Grafik kann wie folgt interpretiert werden:
- Die Wahrscheinlichkeit, dass der Empfangsvektor nicht in das „Sollgebiet” $I_i$ fällt, sondern in das rot hinterlegte Gebiet $I_k$, ist $ {\rm Q} (A/\sigma_n)$. ${\rm Q}(x)$ ist die Gaußsche Fehlerfunktion.
- $A$ bezeichnet den Abstand zwischen $\boldsymbol{ s }_i$ und $G$. $\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an.
- Entsprechend ist die Wahrscheinlichkeit für das Ereignis $r \in I_i$ gleich dem Komplementärwert
- \[{\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) = {\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm} \vert \hspace{0.05cm} m_i ) = 1 - {\rm Q} (A/\sigma_n)\hspace{0.05cm}.\]
Wir betrachten nun die oben angegebenen Gleichungen,
- \[{\rm Pr}({ \cal C} ) = \sum\limits_{i = 0}^{M-1} {\rm Pr}(m_i) \cdot {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) \hspace{0.3cm}{\rm mit} \hspace{0.3cm} {\rm Pr}({ \cal C}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \int_{I_i} p_{{ \boldsymbol{ r }} \hspace{0.05cm}|\hspace{0.05cm}m } (\boldsymbol {\rho } \hspace{0.05cm}|\hspace{0.05cm} m_i ) \,{\rm d} \boldsymbol {\rho } \hspace{0.05cm},\]
etwas genauer, wobei wir wieder von zwei Basisfunktionen $(N = 2)$ und den drei Signalraumpunkten $\boldsymbol{ s }_0$, $\boldsymbol{ s }_1$ und $\boldsymbol{ s }_2$ $(M = 3)$ ausgehen.
- Die Entscheidungsregionen $I_0$, $I_1$ und $I_2$ sind "bestmöglich" gewählt.
- Das AWGN–Rauschen ist in der Skizze durch jeweils drei kreisförmige Höhenlinien angedeutet.
Man erkennt aus dieser Darstellung:
- Unter der Voraussetzung, dass $m = m_i \ \Leftrightarrow \ \boldsymbol{ s } = \boldsymbol{ s }_i$ gesendet wurde, wird nur dann eine richtige Entscheidung getroffen, wenn der Empfangswert $\boldsymbol{ r }$ in der Region $I_i$ liegt.
- Die Wahrscheinlichkeit ${\rm Pr}(\boldsymbol{ r } \in I_i\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist für $i = 2$ (weitaus) am größten ⇒ richtige Entscheidung.
- ${\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm}m_2)$ ist deutlich kleiner. Nahezu vernachlässigbar ist ${\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm}m_2)$.
- Die Verfälschungswahrscheinlichkeiten für $m = m_0$ bzw. $m = m_1$ lauten somit:
- \[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 )={\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ),\]
- \[ {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) ={\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) + {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}.\]
- Die größte Verfälschungswahrscheinlichkeit ergibt sich für $m = m_0$. Wegen
- \[{\rm Pr}(\boldsymbol{ r } \in I_1\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \approx {\rm Pr}(\boldsymbol{ r } \in I_0\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}, \]
- \[{\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_0 ) \gg {\rm Pr}(\boldsymbol{ r } \in I_2\hspace{0.05cm}|\hspace{0.05cm} m_1 ) \hspace{0.05cm}\]
- gelten folgende Relationen:
- $${\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_0 ) > {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_1 ) >{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_2 )\hspace{0.05cm}. $$
$\text{Fazit:}$ Diese Ergebnisse können wie folgt zusammengefasst werden:
- Zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit muss auch bei gleichwahrscheinlichen Symbolen allgemein über alle $M$ Terme gemittelt werden.
- Bei gleichwahrscheinlichen Symbolen kann ${\rm Pr}(m_i) = 1/M$ vor die Summation gezogen werden, was allerdings den Rechengang nicht sonderlich vereinfacht.
- Nur bei symmetrischer Anordnung kann auf die Mittelung ganz verzichtet werden.
Union Bound - Obere Schranke für die Fehlerwahrscheinlichkeit
Bei beliebigen Werten von $M$ gilt für die Verfälschungswahrscheinlichkeit unter der Voraussetzung, dass die Nachricht $m_i$ $($bzw. das Signal $\boldsymbol{s}_i)$ gesendet wurde:
- \[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = {\rm Pr} \left [ \bigcup_{k \ne i} { \cal E}_{ik}\right ] \hspace{0.05cm},\hspace{0.5cm}{ \cal E}_{ik}\hspace{-0.1cm}: \boldsymbol{ r }{\rm \hspace{0.15cm}liegt \hspace{0.15cm}n\ddot{a}her \hspace{0.15cm}bei \hspace{0.15cm}}\boldsymbol{ s }_k {\rm \hspace{0.15cm}als \hspace{0.15cm}beim \hspace{0.15cm}Sollwert \hspace{0.15cm}}\boldsymbol{ s }_i \hspace{0.05cm}. \]
$\text{Definition:}$ Für diesen Ausdruck lässt sich mit einer Booleschen Ungleichung – der so genannten Union Bound – eine obere Schranke angeben:
- \[{\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_i ) \le \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1} {\rm Pr}({ \cal E}_{ik}) = \sum\limits_{k = 0, \hspace{0.1cm}k \ne i}^{M-1}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ]\hspace{0.05cm}. \]
Anmerkungen:
- $d_{ik} = \vert \hspace{-0.05cm} \vert \boldsymbol{s}_i - \boldsymbol{s}_k \vert \hspace{-0.05cm} \vert$ ist der Abstand der Signalraumpunkte $\boldsymbol{s}_i$ und $\boldsymbol{s}_k$.
- $\sigma_n$ gibt den Effektivwert des AWGN–Rauschens an.
- Die "Union Bound" ist nur bei gleichwahrscheinlichen Symbolen ⇒ ${\rm Pr}(m_i) = 1/M$ anwendbar.
- Auch dann muss zur Berechnung der (mittleren) Fehlerwahrscheinlichkeit über alle $m_i$ gemittelt werden.
$\text{Beispiel 5:}$ Die Grafik verdeutlicht die Union Bound am Beispiel $M = 3$ mit gleichwahrscheinlichen Symbolen: ${\rm Pr}(m_0) = {\rm Pr}(m_1) = {\rm Pr}(m_2) =1/3$.
Zu diesen Darstellungen ist anzumerken:
- $${\rm Pr}({ \cal E} ) = 1 - {\rm Pr}({ \cal C} ) \hspace{0.05cm},$$
- $${\rm Pr}({ \cal C} ) = {1}/{3} \cdot \big [ {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_1 ) + {\rm Pr}({ \cal C}\hspace{0.05cm}\vert \hspace{0.05cm} m_2 ) \big ]\hspace{0.05cm}.$$
- Der erste Term ${\rm Pr}(\boldsymbol{r} \in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ im Klammerausdruck unter der Voraussetzung $m = m_0 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_0$ ist in der linken Grafik durch die rote Region $I_0$ visualisiert.
- Die Komplementärregion ${\rm Pr}(\boldsymbol{r} \not\in I_0\hspace{0.05cm}\vert \hspace{0.05cm} m_0)$ ist links entweder blau oder grün oder blau–grün schraffiert markiert. Es gilt ${\rm Pr}({ \cal C}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = 1 - {\rm Pr}({ \cal E}\hspace{0.05cm}\vert \hspace{0.05cm} m_0 )$ mit
- $${\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) = {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\cup \hspace{0.05cm} \boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) $$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Pr}(\boldsymbol{ r } \in I_1 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) + {\rm Pr}(\boldsymbol{ r } \in I_2 \hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) $$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}({ \cal E}\hspace{0.05cm}\vert\hspace{0.05cm} m_0 ) \le {\rm Q} \big [ d_{01}/(2{\sigma_n}) \big ]+ {\rm Q} \big [ d_{02}/(2{\sigma_n}) \big ] \hspace{0.05cm}.$$
- Das „$\le$”–Zeichen berücksichtigt hier, dass die blau–grün schraffierte Fläche sowohl zum Gebiet „$\boldsymbol{r} \in I_1$” als auch zum Gebiet „$\boldsymbol{r} \in I_2$” gehört, so dass die Summe einen zu großen Wert liefert. Das heißt: Die Union Bound liefert stets eine obere Schranke.
- Die mittlere Grafik verdeutlicht die Berechnung der Union Bound unter der Voraussetzung, dass $m = m_1 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_1$ gesendet wurde.
- Dem rechten Bild liegt $m = m_2 \ \Leftrightarrow \ \boldsymbol{s} = \boldsymbol{s}_2$ zugrunde.
Weitere Aufwandsreduzierung bei der Union Bound
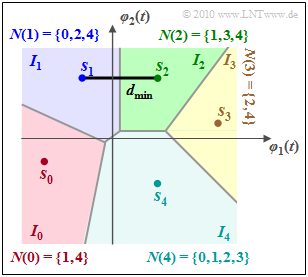
Die Abschätzung nach der „Union Bound” lässt sich weiter verbessern, indem man nur solche Signalraumpunkte berücksichtigt, die direkte Nachbarn des aktuellen Sendevektors $\boldsymbol{s}_i$ sind:
- \[{\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \ne i}^{M-1}{\rm Q}\big [ d_{ik}/(2{\sigma_n}) \big ] \hspace{0.2cm} \Rightarrow \hspace{0.2cm} {\rm Pr}({ \cal E}\hspace{0.05cm}|\hspace{0.05cm} m_i ) = \sum\limits_{k = 0, \hspace{0.1cm} k \hspace{0.05cm}\in \hspace{0.05cm}N(i)}^{M-1}\hspace{-0.4cm}{\rm Q} \big [ d_{ik}/(2{\sigma_n}) \big ] \hspace{0.05cm}. \]
Dazu definieren wir die Nachbarn von $\boldsymbol{s}_i$ als
- \[N(i) = \left \{ k \in \left \{ i = 0, 1, 2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, M-1 \right \}\hspace{0.05cm}|\hspace{0.05cm} I_i {\rm \hspace{0.15cm}grenzt \hspace{0.15cm}direkt \hspace{0.15cm}an \hspace{0.15cm}}I_k \right \} \hspace{0.05cm}. \]
Die Grafik verdeutlicht diese Definiton am Beispiel $M = 5$.
- Die Regionen $I_0$ und $I_3$ haben jeweils nur zwei direkte Nachbarn,
- während $I_4$ an alle anderen Entscheidungsregionen angrenzt.
Durch die Einführung der Nachbarmengen $N(i)$ wird die Qualität der Union Bound–Approximation verbessert, das heißt, die Schranke liegt dann näher an der tatsächlichen Fehlerwahrscheinlichkeit, wird also nach unten verschoben.
Eine weitere Schranke benutzt nur den minimalen Abstand $d_{\rm min}$ zwischen zwei Signalraumpunkten:
- Im obigen Beispiel tritt dieser zwischen $\boldsymbol{s}_1$ und $\boldsymbol{s}_2$ auf.
- Für gleichwahrscheinliche Symbole ⇒ ${\rm Pr}(m_i) =1/M$ gilt dann die folgende Abschätzung:
- \[{\rm Pr}({ \cal E} ) \le \sum\limits_{i = 0 }^{M-1} \left [ {\rm Pr}(m_i) \cdot \sum\limits_{k \ne i }{\rm Q} \big [d_{ik}/(2{\sigma_n})\big ] \right ] \le \frac{1}{M} \cdot \sum\limits_{i = 0 }^{M-1} \left [ \sum\limits_{k \ne i } {\rm Q} [d_{\rm min}/(2{\sigma_n})] \right ] = \sum\limits_{k \ne i }{\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] = (M-1) \cdot {\rm Q} \big [d_{\rm min}/(2{\sigma_n})\big ] \hspace{0.05cm}. \]
Hierzu ist anzumerken:
- Diese Schranke ist auch für große $M$ sehr einfach zu berechnen. Bei vielen Anwendungen ergibt sich jedoch damit eine viel zu große Fehlerwahrscheinlichkeit.
- Die Schranke ist nur dann gleich der tatsächlichen Fehlerwahrscheinlichkeit, wenn die Distanzen aller $M$ Signalpunkte zueinander gleich $d_{\rm min}$ sind.
- Im Sonderfall $M = 2$ ist diese Voraussetzung häufig erfüllt, so dass die Schranke exakt mit der tatsächlichen Fehlerwahrscheinlichkeit übereinstimmt.
Aufgaben zum Kapitel
Aufgabe 4.6: Optimale Entscheidungsgrenze
Aufgabe 4.6Z: Signalraumkonstellationen
Aufgabe 4.7: Nochmals Entscheidungsgrenzen
Aufgabe 4.8: Entscheidungsregionen bei drei Symbolen
Aufgabe 4.8Z: Fehlerwahrscheinlichkeit bei drei Symbolen
Aufgabe 4.9: Entscheidungsregionen bei Laplace
Aufgabe 4.9Z: Laplace-verteiltes Rauschen