Aufgaben:Aufgabe 2.5Z: Lineare Verzerrungen bei ZSB-AM: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Modulationsverfahren/Synchrondemodulation }} [[Datei:|right|]] ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type…“) |
|||
| (16 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
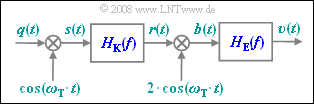
| − | [[Datei:|right|]] | + | [[Datei:P_ID1013__Mod_Z_2_5.png|right|frame|Betrachtes Systemmodell]] |
| + | Untersucht wird hier wie in der [[Aufgaben:2.5_ZSB–AM_über_einen_Gaußkanal|Aufgabe 2.5]] wieder | ||
| + | *die Kombination ZSB–AM/Synchrondemodulator | ||
| + | *bei Berücksichtigung eines linear verzerrenden Kanals . | ||
| + | |||
| + | |||
| + | Das Quellensignal $q(t)$ sei ein Cosinussignal mit Amplitude $A_{\rm N}$ und Frequenz $f_{\rm N}$, so dass das Spektrum des modulierten Signals wie folgt lautet: | ||
| + | :$$S(f)= \frac{A_{\rm N}}{4} \cdot \big[\delta(f + f_{\rm O}) + \delta(f + f_{\rm U}) + \delta(f - f_{\rm U}) + \delta(f - f_{\rm O}) \big]\hspace{0.05cm}.$$ | ||
| + | Die Abkürzungen stehen für $f_{\rm O} = f_{\rm T} + f_{\rm N}$ ('''O'''beres Seitenband) und $f_{\rm U} = f_{\rm T} - f_{\rm N}$ ('''U'''nteres Seitenband). | ||
| + | |||
| + | Der Kanalfrequenzgang ist nur für diese beiden Frequenzen gegeben und lautet: | ||
| + | :$$ H_{\rm K}(f_{\rm O}) = R_{\rm O} + {\rm j} \cdot I_{\rm O},\hspace{0.2cm}H_{\rm K}(f_{\rm U}) = R_{\rm U} + {\rm j} \cdot I_{\rm U} \hspace{0.05cm}.$$ | ||
| + | Für negative Frequenzen gilt stets $H_{\rm K}(– f) = H_{\rm K}^*(f)$. | ||
| + | |||
| + | Verwenden Sie bei numerischen Berechnungen folgende Zahlenwerte: | ||
| + | :$$A_{\rm N} = 2\,{\rm V}, \hspace{0.15cm}f_{\rm N} = 3\,{\rm kHz}, \hspace{0.15cm}f_{\rm T} = 30\,{\rm kHz} \hspace{0.05cm},$$ | ||
| + | :$$R_{\rm U} = 0.8, \hspace{0.15cm}I_{\rm U} = -0.2, \hspace{0.15cm}R_{\rm O} = 0.4, \hspace{0.15cm}I_{\rm O} = -0.2 \hspace{0.05cm}.$$ | ||
| + | In der Teilaufgabe '''(3)''' soll die Lösung über den resultierenden Frequenzgang von Modulator, Kanal und Demodulator erfolgen: | ||
| + | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]\hspace{0.05cm}.$$ | ||
| + | Abschließend wird in der Teilaufgabe '''(4)''' der folgende Kanalfrequenzgang betrachtet (diese Darstellung gilt nur für positive Frequenzen): | ||
| + | :$$ H_{\rm K}(f) = H_{\rm(4)}(f) = \frac{1}{1 + 3{\rm j} \cdot ({f}/{f_{\rm T}} - 1)}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hinweise: | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]]. | ||
| + | *Bezug genommen wird insbesondere auf die Seite [[Modulationsverfahren/Synchrondemodulation#Einfluss_linearer_Kanalverzerrungen|Einfluss linearer Kanalverzerrungen]]. | ||
| + | |||
| + | |||
| Zeile 9: | Zeile 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | |
| − | |type="[] | + | {Es gelte $R_{\rm U} = 0.8, \ I_{\rm U} = -0.2, \ R_{\rm O} = 0.4,\ I_{\rm O} = -0.2.$ Berechnen und skizzieren Sie das Spektrum $R(f)$ am Kanalausgang. <br>Wie lautet die Spektrallinie bei $-f_{\rm O}$? |
| − | - | + | |type="{}"} |
| − | + | ${\rm Re}[R(-f_{\rm O})] \ = \ $ { 0.2 3% } $\ \text{V}$ | |
| + | ${\rm Im}[R(-f_{\rm O})] \ = \ $ { 0.1 3% } $\ \text{V}$ | ||
| − | { | + | {Wie lautet das Sinkensignal $v(t)$? Berücksichtigen Sie bei der Berechnung auch den Tiefpass des Synchrondemodulators. <br>Wie groß ist der Signalwert bei $t = 0$? |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $ v(t = 0) \ = \ $ { 1.2 3% } $\ \text{V}$ |
| − | |||
| + | {Berechnen Sie nun das Sinkensignal $v(t)$ über den resultierenden Frequenzgang $H_{\rm MKD}(f)$ und bewerten Sie den Rechengang. | ||
| + | |type="()"} | ||
| + | - Die Berechnung gemäß Teilaufgabe '''(2)''' führt schneller zum Erfolg. | ||
| + | + Die Berechnung gemäß Teilaufgabe '''(3)''' führt schneller zum Erfolg. | ||
| + | {Berechnen Sie $v(t)$ für den Kanalfrequenzgang $ H_{\rm K}(f) = H_{\rm(4)}(f)$. Wie groß ist der Signalwert bei $t = 0$? | ||
| + | |type="{}"} | ||
| + | $ v(t = 0) \ = \ $ { 1.835 3% } $\ \text{V}$ | ||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
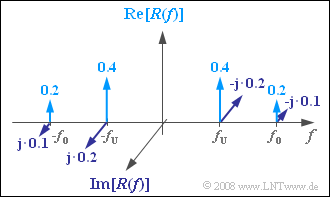
| − | '''1 | + | [[Datei:P_ID1014__Mod_Z_2_5_a.png|right|frame|Spektrum $R(f)$ des Empfangssignals]] |
| − | '''2 | + | '''(1)''' Allgemein gilt $R(f) = S(f) · H_K(f)$. Damit erhält man das Linienspektrum gemäß nebenstehender Skizze (alle Gewichte sind noch um die Einheit „V” zu ergänzen). |
| − | '''3 | + | |
| − | '''4 | + | *Für das Gewicht der Spektrallinie bei $f = -f_{\rm O}$ gilt: |
| − | + | :$${\rm Re}[R(-f_{\rm O})]\hspace{0.15cm}\underline{=0.2 \ \rm V},$$ | |
| − | + | :$${\rm Im}[R(-f_{\rm O})]\hspace{0.15cm}\underline{=0.1 \ \rm V}.$$ | |
| − | + | ||
| + | |||
| + | '''(2)''' Die Spektralfunktion $V(f)$ des Sinkensignals $v(t)$ lautet: | ||
| + | :$$V(f) = \big[ R(f) \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]\big]\cdot H_{\rm E}(f).$$ | ||
| + | *Nach den Gesetzmäßigkeiten der Fouriertransformation kann hierfür auch geschrieben werden: | ||
| + | :$$V(f) = \frac{A_{\rm N}}{4} \cdot (R_{\rm O} + {\rm j} \cdot I_{\rm O}) \cdot \delta(f - f_{\rm N}) + \frac{A_{\rm N}}{4} \cdot (R_{\rm U} + {\rm j} \cdot I_{\rm U}) \cdot \delta(f + f_{\rm N})+$$ | ||
| + | :$$\hspace{2.25cm}+ \frac{A_{\rm N}}{4} \cdot (R_{\rm O} - {\rm j} \cdot I_{\rm O}) \cdot \delta(f + f_{\rm N})+ \frac{A_{\rm N}}{4} \cdot (R_{\rm U} - {\rm j} \cdot I_{\rm U}) \cdot \delta(f - f_{\rm N}) \hspace{0.05cm}.$$ | ||
| + | *Alle anderen Terme liegen um die doppelte Trägerfrequenz und werden durch den Tiefpass eliminiert. | ||
| + | * Umsortieren und Zusammenfassen der Terme führt zu: | ||
| + | :$$V(f) = A_{\rm N}\cdot \frac{R_{\rm U} +R_{\rm O}}{2}\cdot \frac{1}{2} \cdot \left[\delta(f - f_{\rm N}) + \delta(f + f_{\rm N}) \right] + | ||
| + | A_{\rm N}\cdot \frac{I_{\rm U} - I_{\rm O}}{2}\cdot \frac{\rm j}{2} \cdot \left[-\delta(f - f_{\rm N}) + \delta(f + f_{\rm N}) \right]$$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm}v(t) = A_{\rm N}\cdot \frac{R_{\rm U} +R_{\rm O}}{2}\cdot\cos (\omega_{\rm N}\cdot t)+ A_{\rm N}\cdot \frac{I_{\rm U} -I_{\rm O}}{2}\cdot\sin (\omega_{\rm N}\cdot t)\hspace{0.05cm}.$$ | ||
| + | *Mit $R_{\rm U} = 0.8,\ I_{\rm U} = -0.2,\ R_{\rm O} = 0.4,\ I_{\rm O} = -0.2$ folgt daraus: | ||
| + | :$$v(t) = 0.6 \cdot A_{\rm N}\cdot \cos (\omega_{\rm N}\cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} v(t=0) = 0.6 \cdot A_{\rm N}\hspace{0.15cm}\underline {= 1.2\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | *Es ergibt sich gegenüber $q(t)$ eine Dämpfung um den Faktor $0.6$. | ||
| + | *Der Synchrondemodulator bekommt durch das untere Seitenband mehr Information über das Quellensignal als über das obere. | ||
| + | *Wegen der Eigenschaft $I_{\rm O} = I_{\rm U}$ ist $v(t)$ ebenfalls cosinusförmig. | ||
| + | *Es tritt demnach keine Laufzeit auf bzw. die Laufzeit ist ein geradzahliges Vielfaches der Periodendauer. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' Hier gelten folgende Gleichungen: | ||
| + | :$$ H_{\rm K}(f_{\rm N}+ f_{\rm T}) = R_{\rm O} + {\rm j} \cdot I_{\rm O} \hspace{0.05cm}, $$ | ||
| + | :$$ H_{\rm K}(f_{\rm N}- f_{\rm T}) = H_{\rm K}^{\star}(f_{\rm T}- f_{\rm N}) = R_{\rm U} - {\rm j} \cdot I_{\rm U} $$ | ||
| + | :$$\Rightarrow \hspace{0.2cm} H_{\rm MKD}(f_{\rm N}) = {1}/{2} \cdot \big[(R_{\rm O} +R_{\rm U}) + {\rm j} \cdot (I_{\rm O} -I_{\rm U}) \big]\hspace{0.05cm},\hspace{0.2cm} | ||
| + | H_{\rm MKD}(-f_{\rm N}) = H_{\rm MKD}^\star(f_{\rm N}) = {1}/{2} \cdot \big[(R_{\rm O} +R_{\rm U}) - {\rm j} \cdot (I_{\rm O} -I_{\rm U}) \big]\hspace{0.05cm}.$$ | ||
| + | *Man erhält somit das gleiche Ergebnis wie unter (2), aber schneller ⇒ <u>Lösungsvorschlag 2</u>. | ||
| + | |||
| + | |||
| + | |||
| + | '''(4)''' Für $f > 0$ lautet nun der resultierende Frequenzgang: | ||
| + | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \left[ H_{\rm K}(f_{\rm T}+ f) + H_{\rm K}^\star(f_{\rm T}-f)\right]= {1}/{2} \cdot \left[ \frac{1}{1 + 3{\rm j} \cdot (\frac{f_{\rm T}+f}{f_{\rm T}} - 1)} + \frac{1}{1 - 3{\rm j} \cdot (\frac{f_{\rm T}-f}{f_{\rm T}} - 1)}\right] $$ | ||
| + | :$$ \Rightarrow \hspace{0.3cm} H_{\rm MKD}(f) = \frac{1}{1 + {\rm j} \cdot {3f}/{f_{\rm T}} } \hspace{0.05cm}.$$ | ||
| + | *Eingesetzt an der Stelle $f = f_{\rm N}$ führt dies zum Ergebnis: | ||
| + | :$$H_{\rm MKD}(f_{\rm N}) = \frac{1}{1 + {\rm j} \cdot {3f_{\rm N}}/{f_{\rm T}} } \hspace{1.0cm} | ||
| + | \Rightarrow \hspace{0.3cm}{\rm Betrag} = \frac{1}{\sqrt{1 + ({3f_{\rm N}}/{f_{\rm T}} )^2}} \hspace{0.05cm}, \hspace{0.3cm} {\rm Phase} = {\rm arctan}\hspace{0.1cm}({3f_{\rm N}}/{f_{\rm T}}) \hspace{0.05cm}.$$ | ||
| + | *Mit $f_{\rm N}/f_{\rm T} = 0.1$ erhält man den Betrag $0.958$ und die Phase $16.7^\circ$. Damit lautet das Sinkensignal: | ||
| + | :$$v(t) = 0.958 \cdot 2\,{\rm V}\cdot \cos (\omega_{\rm N}\cdot t + 16.7^\circ) \hspace{0.3cm} | ||
| + | \Rightarrow \hspace{0.3cm} v(t=0)= 1.916\,{\rm V}\cdot \cos ( 16.7^\circ)\hspace{0.15cm}\underline { = 1.835\,{\rm V}}\hspace{0.05cm}.$$ | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 8. Dezember 2021, 17:06 Uhr
Untersucht wird hier wie in der Aufgabe 2.5 wieder
- die Kombination ZSB–AM/Synchrondemodulator
- bei Berücksichtigung eines linear verzerrenden Kanals .
Das Quellensignal $q(t)$ sei ein Cosinussignal mit Amplitude $A_{\rm N}$ und Frequenz $f_{\rm N}$, so dass das Spektrum des modulierten Signals wie folgt lautet:
- $$S(f)= \frac{A_{\rm N}}{4} \cdot \big[\delta(f + f_{\rm O}) + \delta(f + f_{\rm U}) + \delta(f - f_{\rm U}) + \delta(f - f_{\rm O}) \big]\hspace{0.05cm}.$$
Die Abkürzungen stehen für $f_{\rm O} = f_{\rm T} + f_{\rm N}$ (Oberes Seitenband) und $f_{\rm U} = f_{\rm T} - f_{\rm N}$ (Unteres Seitenband).
Der Kanalfrequenzgang ist nur für diese beiden Frequenzen gegeben und lautet:
- $$ H_{\rm K}(f_{\rm O}) = R_{\rm O} + {\rm j} \cdot I_{\rm O},\hspace{0.2cm}H_{\rm K}(f_{\rm U}) = R_{\rm U} + {\rm j} \cdot I_{\rm U} \hspace{0.05cm}.$$
Für negative Frequenzen gilt stets $H_{\rm K}(– f) = H_{\rm K}^*(f)$.
Verwenden Sie bei numerischen Berechnungen folgende Zahlenwerte:
- $$A_{\rm N} = 2\,{\rm V}, \hspace{0.15cm}f_{\rm N} = 3\,{\rm kHz}, \hspace{0.15cm}f_{\rm T} = 30\,{\rm kHz} \hspace{0.05cm},$$
- $$R_{\rm U} = 0.8, \hspace{0.15cm}I_{\rm U} = -0.2, \hspace{0.15cm}R_{\rm O} = 0.4, \hspace{0.15cm}I_{\rm O} = -0.2 \hspace{0.05cm}.$$
In der Teilaufgabe (3) soll die Lösung über den resultierenden Frequenzgang von Modulator, Kanal und Demodulator erfolgen:
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]\hspace{0.05cm}.$$
Abschließend wird in der Teilaufgabe (4) der folgende Kanalfrequenzgang betrachtet (diese Darstellung gilt nur für positive Frequenzen):
- $$ H_{\rm K}(f) = H_{\rm(4)}(f) = \frac{1}{1 + 3{\rm j} \cdot ({f}/{f_{\rm T}} - 1)}\hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seite Einfluss linearer Kanalverzerrungen.
Fragebogen
Musterlösung
(1) Allgemein gilt $R(f) = S(f) · H_K(f)$. Damit erhält man das Linienspektrum gemäß nebenstehender Skizze (alle Gewichte sind noch um die Einheit „V” zu ergänzen).
- Für das Gewicht der Spektrallinie bei $f = -f_{\rm O}$ gilt:
- $${\rm Re}[R(-f_{\rm O})]\hspace{0.15cm}\underline{=0.2 \ \rm V},$$
- $${\rm Im}[R(-f_{\rm O})]\hspace{0.15cm}\underline{=0.1 \ \rm V}.$$
(2) Die Spektralfunktion $V(f)$ des Sinkensignals $v(t)$ lautet:
- $$V(f) = \big[ R(f) \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]\big]\cdot H_{\rm E}(f).$$
- Nach den Gesetzmäßigkeiten der Fouriertransformation kann hierfür auch geschrieben werden:
- $$V(f) = \frac{A_{\rm N}}{4} \cdot (R_{\rm O} + {\rm j} \cdot I_{\rm O}) \cdot \delta(f - f_{\rm N}) + \frac{A_{\rm N}}{4} \cdot (R_{\rm U} + {\rm j} \cdot I_{\rm U}) \cdot \delta(f + f_{\rm N})+$$
- $$\hspace{2.25cm}+ \frac{A_{\rm N}}{4} \cdot (R_{\rm O} - {\rm j} \cdot I_{\rm O}) \cdot \delta(f + f_{\rm N})+ \frac{A_{\rm N}}{4} \cdot (R_{\rm U} - {\rm j} \cdot I_{\rm U}) \cdot \delta(f - f_{\rm N}) \hspace{0.05cm}.$$
- Alle anderen Terme liegen um die doppelte Trägerfrequenz und werden durch den Tiefpass eliminiert.
- Umsortieren und Zusammenfassen der Terme führt zu:
- $$V(f) = A_{\rm N}\cdot \frac{R_{\rm U} +R_{\rm O}}{2}\cdot \frac{1}{2} \cdot \left[\delta(f - f_{\rm N}) + \delta(f + f_{\rm N}) \right] + A_{\rm N}\cdot \frac{I_{\rm U} - I_{\rm O}}{2}\cdot \frac{\rm j}{2} \cdot \left[-\delta(f - f_{\rm N}) + \delta(f + f_{\rm N}) \right]$$
- $$ \Rightarrow \hspace{0.3cm}v(t) = A_{\rm N}\cdot \frac{R_{\rm U} +R_{\rm O}}{2}\cdot\cos (\omega_{\rm N}\cdot t)+ A_{\rm N}\cdot \frac{I_{\rm U} -I_{\rm O}}{2}\cdot\sin (\omega_{\rm N}\cdot t)\hspace{0.05cm}.$$
- Mit $R_{\rm U} = 0.8,\ I_{\rm U} = -0.2,\ R_{\rm O} = 0.4,\ I_{\rm O} = -0.2$ folgt daraus:
- $$v(t) = 0.6 \cdot A_{\rm N}\cdot \cos (\omega_{\rm N}\cdot t)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} v(t=0) = 0.6 \cdot A_{\rm N}\hspace{0.15cm}\underline {= 1.2\,{\rm V}}\hspace{0.05cm}.$$
- Es ergibt sich gegenüber $q(t)$ eine Dämpfung um den Faktor $0.6$.
- Der Synchrondemodulator bekommt durch das untere Seitenband mehr Information über das Quellensignal als über das obere.
- Wegen der Eigenschaft $I_{\rm O} = I_{\rm U}$ ist $v(t)$ ebenfalls cosinusförmig.
- Es tritt demnach keine Laufzeit auf bzw. die Laufzeit ist ein geradzahliges Vielfaches der Periodendauer.
(3) Hier gelten folgende Gleichungen:
- $$ H_{\rm K}(f_{\rm N}+ f_{\rm T}) = R_{\rm O} + {\rm j} \cdot I_{\rm O} \hspace{0.05cm}, $$
- $$ H_{\rm K}(f_{\rm N}- f_{\rm T}) = H_{\rm K}^{\star}(f_{\rm T}- f_{\rm N}) = R_{\rm U} - {\rm j} \cdot I_{\rm U} $$
- $$\Rightarrow \hspace{0.2cm} H_{\rm MKD}(f_{\rm N}) = {1}/{2} \cdot \big[(R_{\rm O} +R_{\rm U}) + {\rm j} \cdot (I_{\rm O} -I_{\rm U}) \big]\hspace{0.05cm},\hspace{0.2cm} H_{\rm MKD}(-f_{\rm N}) = H_{\rm MKD}^\star(f_{\rm N}) = {1}/{2} \cdot \big[(R_{\rm O} +R_{\rm U}) - {\rm j} \cdot (I_{\rm O} -I_{\rm U}) \big]\hspace{0.05cm}.$$
- Man erhält somit das gleiche Ergebnis wie unter (2), aber schneller ⇒ Lösungsvorschlag 2.
(4) Für $f > 0$ lautet nun der resultierende Frequenzgang:
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \left[ H_{\rm K}(f_{\rm T}+ f) + H_{\rm K}^\star(f_{\rm T}-f)\right]= {1}/{2} \cdot \left[ \frac{1}{1 + 3{\rm j} \cdot (\frac{f_{\rm T}+f}{f_{\rm T}} - 1)} + \frac{1}{1 - 3{\rm j} \cdot (\frac{f_{\rm T}-f}{f_{\rm T}} - 1)}\right] $$
- $$ \Rightarrow \hspace{0.3cm} H_{\rm MKD}(f) = \frac{1}{1 + {\rm j} \cdot {3f}/{f_{\rm T}} } \hspace{0.05cm}.$$
- Eingesetzt an der Stelle $f = f_{\rm N}$ führt dies zum Ergebnis:
- $$H_{\rm MKD}(f_{\rm N}) = \frac{1}{1 + {\rm j} \cdot {3f_{\rm N}}/{f_{\rm T}} } \hspace{1.0cm} \Rightarrow \hspace{0.3cm}{\rm Betrag} = \frac{1}{\sqrt{1 + ({3f_{\rm N}}/{f_{\rm T}} )^2}} \hspace{0.05cm}, \hspace{0.3cm} {\rm Phase} = {\rm arctan}\hspace{0.1cm}({3f_{\rm N}}/{f_{\rm T}}) \hspace{0.05cm}.$$
- Mit $f_{\rm N}/f_{\rm T} = 0.1$ erhält man den Betrag $0.958$ und die Phase $16.7^\circ$. Damit lautet das Sinkensignal:
- $$v(t) = 0.958 \cdot 2\,{\rm V}\cdot \cos (\omega_{\rm N}\cdot t + 16.7^\circ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t=0)= 1.916\,{\rm V}\cdot \cos ( 16.7^\circ)\hspace{0.15cm}\underline { = 1.835\,{\rm V}}\hspace{0.05cm}.$$