Aufgaben:Aufgabe 2.6Z: Signal–zu–Rausch–Leistungsverhältnis: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
|||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
}} | }} | ||
| − | [[Datei:P_ID1017__Mod_Z_2_6.png|right|]] | + | [[Datei:P_ID1017__Mod_Z_2_6.png|right|frame|Spektren und Leistungsdichtespektren]] |
| − | Wir gehen von folgenden Voraussetzungen aus: | + | Wir gehen in dieser Aufgabe von folgenden Voraussetzungen aus: |
| − | + | *ein cosinusförmiges Quellensignal: | |
| − | $$ q(t) = 4 \,{\rm V} \cdot \cos(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm},$$ | + | :$$ q(t) = 4 \,{\rm V} \cdot \cos(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm},$$ |
| − | + | * ZSB–AM durch Multiplikation mit | |
| − | $$z(t) = 1 \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t )\hspace{0.05cm},$$ | + | :$$z(t) = 1 \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t )\hspace{0.05cm},$$ |
| − | + | * eine frequenzunabhängige Dämpfung auf dem Kanal entsprechend $α_{\rm K} = 10^{–4}$, | |
| − | + | * additives weißes Eingangsrauschen mit Rauschleistungsdichte $N_0 = 4 · 10^{–19} \ \rm W/Hz$, | |
| − | + | * phasen– und frequenzsynchrone Demodulation durch Multiplikation mit gleichem $z(t)$ wie beim Sender, | |
| − | + | * ein rechteckförmiger Tiefpass beim Synchrondemodulator mit Grenzfrequenz $f_{\rm E} = 5 \ \rm kHz$. | |
| − | In der Grafik sind diese Vorgaben im Spektralbereich dargestellt. Ausdrücklich soll erwähnt werden, dass das Leistungsdichtespektrum $ | + | In der Grafik sind diese Vorgaben im Spektralbereich dargestellt. Ausdrücklich soll erwähnt werden, dass sich das Leistungsdichtespektrum ${\it Φ}_z(f)$ der Cosinusschwingung $z(t)$ ebenso wie das Amplitudenspektrum $Z(f)$ aus zwei Diraclinien bei $±f_{\rm T}$ zusammensetzt, aber mit dem Gewicht $A^2/4$ anstelle von $A/2$. Die Amplitude ist bei dieser Aufgabe stets $A=1$ zu setzen. |
| − | Das Sinkensignal $ | + | Das Sinkensignal $v(t)$ setzt sich aus dem Nutzanteil $α · q(t)$ und dem Rauschanteil $ε(t)$ zusammen. Somit gilt allgemein für das zu bestimmende Signal–zu–Rausch–Leistungsverhältnis: |
| − | $$ \rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon}\hspace{0.05cm}.$$ | + | :$$ \rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon}\hspace{0.05cm}.$$ |
| − | Dieses wichtige Qualitätskriterium wird häufig mit SNR (englisch: | + | Dieses wichtige Qualitätskriterium wird häufig mit $\rm SNR$ (englisch: "signal–to–noise power ratio") abgekürzt. |
| − | + | ||
| − | + | ||
| − | + | Hinweise: | |
| − | + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Synchrondemodulation|Synchrondemodulation]]. | |
| + | *Bezug genommen wird insbesondere auf die Seiten <br> [[Modulationsverfahren/Synchrondemodulation#Berechnung_der_Rauschleistung|Berechnung der Rauschleistung]] sowie <br> [[Modulationsverfahren/Synchrondemodulation#Zusammenhang_zwischen_den_Leistungen_von_Quellensignal_und_Sendesignal|Zusammenhang zwischen den Leistungen von Quellensignal und Sendesignal]]. | ||
| + | *Beachten Sie bitte auch, dass die Größen $α$ und $α_{\rm K}$ nicht unbedingt gleich sein müssen. | ||
| + | *Alle Leistungen mit Ausnahme der Teilaufgabe '''(1)''' beziehen sich auf den Widerstand $R = 50 \ \rm Ω$. | ||
| + | *$P_q$ gibt bei „ZSB–AM ohne Träger” gleichzeitig die Sendeleistung $P_{\rm S}$ an. | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
| Zeile 31: | Zeile 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | + | {Berechnen Sie die Sendeleistung bezogen auf den Einheitswiderstand $R = 1 \ \rm Ω$. | |
| − | {Berechnen Sie die Sendeleistung | ||
|type="{}"} | |type="{}"} | ||
| − | $P_q$ | + | $P_q \ = \ $ { 8 3% } $\ \rm V^2$ |
| − | {Wie groß ist die Leistung $P_q$ in | + | {Wie groß ist die Leistung $P_q$ in „Watt” für den Widerstand $R = 50 \ \rm Ω$? |
|type="{}"} | |type="{}"} | ||
| − | $P_q$ | + | $P_q \ = \ $ { 0.16 3% } $\ \rm W$ |
| − | {Welcher Dämpfungsfaktor ergibt sich für das Gesamtsystem? | + | {Welcher Dämpfungsfaktor $α$ ergibt sich für das Gesamtsystem? |
|type="{}"} | |type="{}"} | ||
| − | $α$ | + | $α \ = \ $ { 0.5 3% } $\ \cdot 10^{-4}$ |
| − | {Berechnen Sie die Leistungsdichte der Rauschkomponente $ε(t)$ am Ausgang. Wie groß ist der Wert bei $f = 0$? Es gelte $ | + | {Berechnen Sie die Leistungsdichte der Rauschkomponente $ε(t)$ am Ausgang. Wie groß ist der Wert bei $f = 0$? Es gelte $H_{\rm E}(f = 0) = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | ${\it Φ}_ε(f = 0) \ = \ $ { 4 3% } $\ \cdot 10^{-19} \ \rm W/Hz$ |
{Wie groß ist die Rauschleistung im Sinkensignal? | {Wie groß ist die Rauschleistung im Sinkensignal? | ||
|type="{}"} | |type="{}"} | ||
| − | $P_ε$ | + | $P_ε \ = \ $ { 4 3% } $\ \cdot 10^{-15} \ \rm W$ |
| − | {Wie groß ist das Signal–zu–Rausch–Leistungsverhältnis (SNR) an der Sinke? Welcher | + | {Wie groß ist das Signal–zu–Rausch–Leistungsverhältnis (SNR) an der Sinke? Welcher dB–Wert ergibt sich daraus? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ρ_v \ = \ $ { 100000 3% } |
| − | $10 · lg | + | $10 · \lg ρ_v \ = \ $ { 50 3% } $\ \rm dB$ |
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Das Leistungsdichtespektrum eines Cosinussignals mit der Amplitude $A$ besteht aus zwei Diraclinien, jeweils mit Gewicht $A^2/4$. |
| − | $$ P_q = \frac{A^2}{2} \hspace{0.15cm}\underline {= 8\,{\rm V^2}} \hspace{0.05cm}.$$ | + | *Die Leistung ergibt sich aus dem Integral über das LDS und ist somit gleich der Summe der beiden Diracgewichte. |
| − | Beim Modulationsverfahren „ZSB-AM ohne Träger” ist dies gleichzeitig die auf den Einheitswiderstand 1 Ω bezogene Sendeleistung. | + | *Mit $A = 4 \ \rm V$ erhält man somit für die Leistung des Quellensignals: |
| + | :$$ P_q = \frac{A^2}{2} \hspace{0.15cm}\underline {= 8\,{\rm V^2}} \hspace{0.05cm}.$$ | ||
| + | *Beim Modulationsverfahren „ZSB-AM ohne Träger” ist dies gleichzeitig die auf den Einheitswiderstand $1\ \rm Ω$ bezogene Sendeleistung $P_{\rm S}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Nach den elementaren Gesetzen der Elektrotechnik gilt: | ||
| + | :$$P_q = \frac{8\,{\rm V^2}}{50\,{\Omega}} \hspace{0.15cm}\underline {= 0.16\,{\rm W}} \hspace{0.05cm}.$$ | ||
| + | |||
| + | '''(3)''' Im Theorieteil wird gezeigt, dass bei idealen Voraussetzungen $v(t) = q(t)$ gilt. Zu berücksichtigen ist allerdings: | ||
| + | *Aus der Grafik erkennt man, dass $Z_{\rm E}(f) = Z(f)$ gilt. Damit hat das empfängerseitige Trägersignal $z_{\rm E}(t)$ wie $z(t)$ die Amplitude $1$. | ||
| + | *Im Idealfall müsste aber das empfängerseitige Trägersignal $z_{\rm E}(t)$ die Amplitude $2$ besitzen. | ||
| + | *Deshalb gilt gilt hier $υ(t) = q(t)/2$. | ||
| + | *Berücksichtigt man weiter die Kanaldämpfung $α_{\rm K} = 10^{–4}$, so erhält man das Endergebnis: $α\hspace{0.15cm}\underline { = 0.5 · 10^{–4}}.$ | ||
| − | |||
| − | |||
| − | ''' | + | '''(4)''' Das Leistungsdichtespektrum des Produktes $n(t) · z(t)$ ergibt sich aus der Faltung der beiden Leistungsdichtespektren von $n(t)$ und $z(t)$: |
| + | :$$ {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) = {\it \Phi}_n (f) \star {\it \Phi}_{z }(f)= \frac{N_0}{2} \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]= N_0 \hspace{0.05cm}.$$ | ||
| + | *Für das Leistungsdichtespektrum des Signals $ε(t)$ nach dem Tiefpass erhält man eine Rechteckform mit dem gleichen Wert bei $f = 0$: | ||
| + | :$${\it \Phi}_\varepsilon (f) = {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) \cdot |H_{\rm E}(f)|^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\it \Phi}_\varepsilon (f=0)= N_0\hspace{0.15cm}\underline {= 4 \cdot 10^{-19}\,{\rm W/Hz}} \hspace{0.05cm}.$$ | ||
| − | ''' | + | '''(5)''' Die Rauschleistung ist das Integral über die Rauschleistungsdichte: |
| − | $$ { | + | :$$ P_{\varepsilon} = \int_{-f_{\rm E}}^{ + f_{\rm E}} {{\it \Phi}_\varepsilon (f)}\hspace{0.1cm}{\rm d}f = N_0 \cdot 2 f_{\rm E} = 4 \cdot 10^{-19}\,\frac{ \rm W}{\rm Hz} \cdot 10^{4}\,{\rm Hz} \hspace{0.15cm}\underline {= 4 \cdot 10^{-15}\,{\rm W}}\hspace{0.05cm}.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''6 | + | '''(6)''' Aus den Ergebnissen der Teilaufgaben '''(2)''', '''(3)''' und '''(5)''' folgt: |
| − | $$\rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon} = \frac{(0.5 \cdot 10^{-4})^2 \cdot 0.16\,{\rm W}}{4 \cdot 10^{-15}\,{\rm W}} \hspace{0.15cm}\underline {= | + | :$$\rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon} = \frac{(0.5 \cdot 10^{-4})^2 \cdot 0.16\,{\rm W}}{4 \cdot 10^{-15}\,{\rm W}} \hspace{0.15cm}\underline {= 100000} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg }\hspace{0.1cm}\rho_{v } \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Aktuelle Version vom 9. Dezember 2021, 14:54 Uhr
Wir gehen in dieser Aufgabe von folgenden Voraussetzungen aus:
- ein cosinusförmiges Quellensignal:
- $$ q(t) = 4 \,{\rm V} \cdot \cos(2 \pi \cdot 5\,{\rm kHz} \cdot t )\hspace{0.05cm},$$
- ZSB–AM durch Multiplikation mit
- $$z(t) = 1 \cdot \cos(2 \pi \cdot 20\,{\rm kHz} \cdot t )\hspace{0.05cm},$$
- eine frequenzunabhängige Dämpfung auf dem Kanal entsprechend $α_{\rm K} = 10^{–4}$,
- additives weißes Eingangsrauschen mit Rauschleistungsdichte $N_0 = 4 · 10^{–19} \ \rm W/Hz$,
- phasen– und frequenzsynchrone Demodulation durch Multiplikation mit gleichem $z(t)$ wie beim Sender,
- ein rechteckförmiger Tiefpass beim Synchrondemodulator mit Grenzfrequenz $f_{\rm E} = 5 \ \rm kHz$.
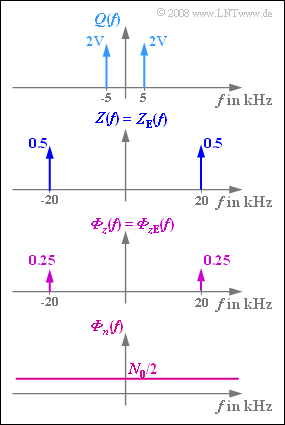
In der Grafik sind diese Vorgaben im Spektralbereich dargestellt. Ausdrücklich soll erwähnt werden, dass sich das Leistungsdichtespektrum ${\it Φ}_z(f)$ der Cosinusschwingung $z(t)$ ebenso wie das Amplitudenspektrum $Z(f)$ aus zwei Diraclinien bei $±f_{\rm T}$ zusammensetzt, aber mit dem Gewicht $A^2/4$ anstelle von $A/2$. Die Amplitude ist bei dieser Aufgabe stets $A=1$ zu setzen.
Das Sinkensignal $v(t)$ setzt sich aus dem Nutzanteil $α · q(t)$ und dem Rauschanteil $ε(t)$ zusammen. Somit gilt allgemein für das zu bestimmende Signal–zu–Rausch–Leistungsverhältnis:
- $$ \rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon}\hspace{0.05cm}.$$
Dieses wichtige Qualitätskriterium wird häufig mit $\rm SNR$ (englisch: "signal–to–noise power ratio") abgekürzt.
Hinweise:
- Die Aufgabe gehört zum Kapitel Synchrondemodulation.
- Bezug genommen wird insbesondere auf die Seiten
Berechnung der Rauschleistung sowie
Zusammenhang zwischen den Leistungen von Quellensignal und Sendesignal. - Beachten Sie bitte auch, dass die Größen $α$ und $α_{\rm K}$ nicht unbedingt gleich sein müssen.
- Alle Leistungen mit Ausnahme der Teilaufgabe (1) beziehen sich auf den Widerstand $R = 50 \ \rm Ω$.
- $P_q$ gibt bei „ZSB–AM ohne Träger” gleichzeitig die Sendeleistung $P_{\rm S}$ an.
Fragebogen
Musterlösung
- Die Leistung ergibt sich aus dem Integral über das LDS und ist somit gleich der Summe der beiden Diracgewichte.
- Mit $A = 4 \ \rm V$ erhält man somit für die Leistung des Quellensignals:
- $$ P_q = \frac{A^2}{2} \hspace{0.15cm}\underline {= 8\,{\rm V^2}} \hspace{0.05cm}.$$
- Beim Modulationsverfahren „ZSB-AM ohne Träger” ist dies gleichzeitig die auf den Einheitswiderstand $1\ \rm Ω$ bezogene Sendeleistung $P_{\rm S}$.
(2) Nach den elementaren Gesetzen der Elektrotechnik gilt:
- $$P_q = \frac{8\,{\rm V^2}}{50\,{\Omega}} \hspace{0.15cm}\underline {= 0.16\,{\rm W}} \hspace{0.05cm}.$$
(3) Im Theorieteil wird gezeigt, dass bei idealen Voraussetzungen $v(t) = q(t)$ gilt. Zu berücksichtigen ist allerdings:
- Aus der Grafik erkennt man, dass $Z_{\rm E}(f) = Z(f)$ gilt. Damit hat das empfängerseitige Trägersignal $z_{\rm E}(t)$ wie $z(t)$ die Amplitude $1$.
- Im Idealfall müsste aber das empfängerseitige Trägersignal $z_{\rm E}(t)$ die Amplitude $2$ besitzen.
- Deshalb gilt gilt hier $υ(t) = q(t)/2$.
- Berücksichtigt man weiter die Kanaldämpfung $α_{\rm K} = 10^{–4}$, so erhält man das Endergebnis: $α\hspace{0.15cm}\underline { = 0.5 · 10^{–4}}.$
(4) Das Leistungsdichtespektrum des Produktes $n(t) · z(t)$ ergibt sich aus der Faltung der beiden Leistungsdichtespektren von $n(t)$ und $z(t)$:
- $$ {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) = {\it \Phi}_n (f) \star {\it \Phi}_{z }(f)= \frac{N_0}{2} \star \left[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \right]= N_0 \hspace{0.05cm}.$$
- Für das Leistungsdichtespektrum des Signals $ε(t)$ nach dem Tiefpass erhält man eine Rechteckform mit dem gleichen Wert bei $f = 0$:
- $${\it \Phi}_\varepsilon (f) = {\it \Phi}_\varepsilon \hspace{0.01cm} '(f) \cdot |H_{\rm E}(f)|^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\it \Phi}_\varepsilon (f=0)= N_0\hspace{0.15cm}\underline {= 4 \cdot 10^{-19}\,{\rm W/Hz}} \hspace{0.05cm}.$$
(5) Die Rauschleistung ist das Integral über die Rauschleistungsdichte:
- $$ P_{\varepsilon} = \int_{-f_{\rm E}}^{ + f_{\rm E}} {{\it \Phi}_\varepsilon (f)}\hspace{0.1cm}{\rm d}f = N_0 \cdot 2 f_{\rm E} = 4 \cdot 10^{-19}\,\frac{ \rm W}{\rm Hz} \cdot 10^{4}\,{\rm Hz} \hspace{0.15cm}\underline {= 4 \cdot 10^{-15}\,{\rm W}}\hspace{0.05cm}.$$
(6) Aus den Ergebnissen der Teilaufgaben (2), (3) und (5) folgt:
- $$\rho_{v } = \frac{\alpha^2 \cdot P_q}{P_\varepsilon} = \frac{(0.5 \cdot 10^{-4})^2 \cdot 0.16\,{\rm W}}{4 \cdot 10^{-15}\,{\rm W}} \hspace{0.15cm}\underline {= 100000} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg }\hspace{0.1cm}\rho_{v } \hspace{0.15cm}\underline {= 50\,{\rm dB}}\hspace{0.05cm}.$$