Aufgaben:Aufgabe 3.11: Pre-emphase und De-emphase: Unterschied zwischen den Versionen
Safwen (Diskussion | Beiträge) |
K (Guenter verschob die Seite Aufgabe 3.11: Preemphase und Deemphase nach Aufgabe 3.11: Pre-emphase und De-emphase) |
||
| (15 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{quiz-Header|Buchseite=Modulationsverfahren/ | + | {{quiz-Header|Buchseite=Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation |
}} | }} | ||
| − | [[Datei:P_ID1116__Mod_A_3_10.png|right|]] | + | [[Datei:P_ID1116__Mod_A_3_10.png|right|frame|Realisierung einer Preemphase]] |
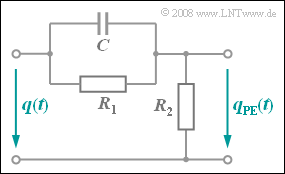
| − | Bei der Sprach– und Tonsignalübertragung wird das Signalfrequenzband vor dem FM–Modulator über ein RC–Hochpassglied gemäß der Skizze vorverzerrt. Man bezeichnet diese Maßnahme als Preemphase. | + | Bei der Sprach– und Tonsignalübertragung wird das Signalfrequenzband vor dem FM–Modulator über ein RC–Hochpassglied gemäß der Skizze vorverzerrt. Man bezeichnet diese Maßnahme als „Preemphase” $\rm (PE)$. |
| − | Der Amplitudengang des Preemphase–Netzwerks lautet mit den beiden Grenzfrequenzen $f_{G1} = (2π · R_1 · C)^{–1}$ und $f_{G2} = f_{G1}/α_0$ sowie dem | + | Der Amplitudengang des Preemphase–Netzwerks lautet |
| − | $$ |H_{\rm PE} (f)| = \alpha_0 \cdot \sqrt{\frac{1 + (f/f_{\rm G1})^2}{1 + (f/f_{\rm G2})^2}} \hspace{0.05cm}.$$ | + | *mit den beiden Grenzfrequenzen $f_{\rm G1} = (2π · R_1 · C)^{–1}$ und $f_{\rm G2} = f_{\rm G1}/α_0$, sowie |
| − | + | *dem Gleichsignalübertragungsfaktor $α_0 = R_2/(R_1 + R_2)$: | |
| − | + | :$$ |H_{\rm PE} (f)| = \alpha_0 \cdot \sqrt{\frac{1 + (f/f_{\rm G1})^2}{1 + (f/f_{\rm G2})^2}} \hspace{0.05cm}.$$ | |
| − | |||
| − | |||
| − | |||
| + | Für die Praxis kann man davon ausgehen, dass die maximale Nachrichtenfrequenz $f_{\rm N}$ sehr viel kleiner als $f_{\rm G2}$ ist. | ||
| − | + | Berücksichtigt man weiter, dass der Gleichsignalübertragungsfaktor $α_0$ durch eine Verstärkung um $α$ verändert werden kann, so ist im Weiteren von folgendem Preemphase–Frequenzgang auszugehen $(f_{\rm G} = f_{\rm G1} = 3 \ \rm kHz)$: | |
| + | :$$|H_{\rm PE} (f)| \approx \alpha \cdot \sqrt{{1 + \left({f}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$ | ||
| + | Mit diesem Netzwerk lautet der Frequenzhub $Δf_{\rm A}$ in Abhängigkeit der Nachrichtenfrequenz $f_{\rm N}$: | ||
| + | :$$ \Delta f_{\rm A} (f_{\rm N}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left({f_{\rm N}}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$ | ||
| + | *Hierbei ist $Δf_\text{A, min}$ der Frequenzhub für sehr kleine Frequenzen $(f_{\rm N} → 0)$. | ||
| + | *Dieser Parameter ist so zu wählen, dass der maximale Frequenzhub $Δf_\text{A, max}$ nicht größer wird als $45 \ \rm kHz$. | ||
| − | Um das Nutzsignal nicht zu verfälschen, muss diese Vorverzerrung durch ein | + | Um das Nutzsignal nicht zu verfälschen, muss diese Vorverzerrung durch ein „Deemphase”–Netzwerk beim Empfänger wieder ausgeglichen werden. Ziel und Zweck von Preemphase/Deemphase ist es allein, die Abhängigkeit des Signal–zu–Rausch–Leistungsverhältnisses von der Signalfrequenz zu vermindern. |
In dieser Aufgabe werden folgende Größen verwendet: | In dieser Aufgabe werden folgende Größen verwendet: | ||
| − | + | * Sinken–SNR bei Zweiseitenband-Amplitudenmodulation $\rm (ZSB–AM)$: | |
| − | $$\rho_{{\rm AM} } = \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} } = \xi\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{{\rm AM} } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.05cm},$$ | + | :$$\rho_{{\rm AM} } = \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} } = \xi\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{{\rm AM} } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.05cm},$$ |
| − | + | * Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation $\rm (FM)$ ohne Preemphase/Deemphase: | |
| − | $$ \rho_{ FM} = {3}/{2 } \cdot \eta^2 \cdot \rho_ | + | :$$ \rho_{\rm FM} = {3}/{2 } \cdot \eta^2 \cdot \rho_{\rm AM } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |
| − | + | G_{\rm FM} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM} - | |
| − | $$ \rho_{ DE} = \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{ DE} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{ DE} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{ FM}\hspace{0.05cm} | + | 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm AM}= 10 \cdot {\rm |
| − | + | lg} \hspace{0.15cm}{3}/{2 } \cdot \eta^2 | |
| + | \hspace{0.05cm},$$ | ||
| + | *Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation $\rm (FM)$ durch Preemphase/Deemphase: | ||
| + | :$$ \rho_{\rm DE} = \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) } | ||
| + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | G_{\rm DE} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm DE} - | ||
| + | 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM}\hspace{0.05cm}$$ | ||
| + | |||
| + | |||
| + | |||
| + | ''Hinweise:'' | ||
| + | *Die Aufgabe gehört zum Kapitel [[Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation|Rauscheinfluss bei Winkelmodulation]]. | ||
| + | *Bezug genommen wirdinsbesondere auf den Abschnitt [[Modulationsverfahren/Rauscheinfluss_bei_Winkelmodulation#Preemphase_und_Deemphase|Preemphase und Deemphase]]. | ||
| + | *Gehen Sie in der gesamten Aufgabe von einem Nachrichtensignal aus, das Frequenzen bis einschließlich $B_{\rm NF}= 9 \ \rm kHz$ beinhaltet. | ||
| + | |||
| Zeile 36: | Zeile 53: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Geben Sie eine mögliche Realisierung des Deemphase–Netzwerks $H_{DE}(f)$ an. Welche der | + | {Geben Sie eine mögliche Realisierung des Deemphase–Netzwerks $H_{\rm DE}(f)$ an. Welche der folgenden Aussagen sind richtig? |
|type="[]"} | |type="[]"} | ||
| − | + $H_{DE}(f)$ ist ein Tiefpass erster Ordnung. | + | + $H_{\rm DE}(f)$ ist ein Tiefpass erster Ordnung. |
| − | - $H_{DE}(f)$ ist ein Hochpass erster Ordnung. | + | - $H_{\rm DE}(f)$ ist ein Hochpass erster Ordnung. |
| − | - $H_{DE}(f)$ ist ein Bandpass. | + | - $H_{\rm DE}(f)$ ist ein Bandpass. |
| − | + Zusätzlich muss der Faktor $α$ korrigiert werden. | + | + Zusätzlich muss der Faktor $α$ korrigiert werden. |
| − | {Wie groß ist der Störabstandsgewinn der herkömmlichen FM gegenüber AM | + | {Wie groß ist der Störabstandsgewinn $G_{\rm FM}$ der herkömmlichen FM gegenüber AM bei den genannten Nachrichtenfrequenzen $ f_{\rm N}$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ f_{\rm N} = \text{9 kHz:} \hspace{0.2cm} G_{\rm FM} \ = \ $ { 15.74 3% } $\ \rm dB$ |
| − | $ | + | $ f_{\rm N} = \text{3 kHz:} \hspace{0.2cm} G_{\rm FM} \ = \ $ { 25.28 3% } $\ \rm dB$ |
| − | $ | + | $ f_{\rm N} = \text{1 kHz:} \hspace{0.2cm} G_{\rm FM} \ = \ $ { 34.82 3% } $\ \rm dB$ |
| − | {Wie groß ist $Δf_{A, min}$ mit $Δf_{A, max} = 45 kHz$ und $B_{NF} = 9 kHz$ zu wählen? | + | {Wie groß ist $Δf_\text{A, min}$ mit $Δf_\text{A, max} = 45 \ \rm kHz$ und $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ zu wählen? |
|type="{}"} | |type="{}"} | ||
| − | $Δf_{A, min} | + | $Δf_\text{A, min} \ = \ $ { 14.23 3% } $\ \rm kHz$ |
{Welcher zusätzliche Gewinn ist durch Preemphase/Deemphase zu erzielen? | {Welcher zusätzliche Gewinn ist durch Preemphase/Deemphase zu erzielen? | ||
|type="{}"} | |type="{}"} | ||
| − | $ | + | $ f_{\rm N} = \text{9 kHz:} \hspace{0.2cm} G_{\rm DE} \ = \ $ { 7.1 3% } $\ \rm dB$ |
| − | $ | + | $ f_{\rm N} = \text{3 kHz:} \hspace{0.2cm} G_{\rm DE} \ = \ $ { 1.9 3% } $\ \rm dB$ |
| − | $ | + | $ f_{\rm N} = \text{1 kHz:} \hspace{0.2cm} G_{\rm DE} \ = \ $ { 0.28 3% } $\ \rm dB$ |
| Zeile 69: | Zeile 86: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' Richtig sind <u>der erste und der letzte Lösungsvorschlag</u>: |
| − | $$ |H_{\rm DE} (f)| = \frac{1}{|H_{\rm PE} (f)|}= \frac{1}{\alpha}\cdot \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}} \hspace{0.05cm}.$$ | + | *Der Betragsfrequenzgang des Deemphase–Netzwerks ist wie folgt festgelegt: |
| − | Der Frequenzgang eines einfachen RC–Tiefpasses – auch bekannt als Tiefpass erster Ordnung – lautet: | + | :$$ |H_{\rm DE} (f)| = \frac{1}{|H_{\rm PE} (f)|}= \frac{1}{\alpha}\cdot \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}} \hspace{0.05cm}.$$ |
| − | $$ H_{\rm | + | *Der Frequenzgang eines einfachen RC–Tiefpasses – auch bekannt als Tiefpass erster Ordnung – lautet: |
| − | + | :$$ H_{\rm RC-TP} (f) = \frac{1}{{1 + {\rm j}\cdot f/f_{\rm G}}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |H_{\rm RC-TP} (f)| = \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}}\hspace{0.05cm}.$$ | |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Die Frequenzmodulation ist auf die maximale Frequenz $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ ausgelegt. Dann soll der (maximale) Frequenzhub $Δf_{\rm A} = 45\ \rm kHz$ betragen. | ||
| + | *Daraus folgt für den Modulationsindex: | ||
| + | :$$ \eta = \frac{\Delta f_{\rm A}}{f_{\rm N} } = 5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| + | G_{\rm FM} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg} | ||
| + | \hspace{0.15cm}(1.5 \cdot 5^2) \hspace{0.15cm}\underline {\approx 15.74\,{\rm dB}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Mit der Nachrichtenfrequenz $ f_{\rm N} = 3 \ \rm kHz$ ergibt sich ein um den Faktor $3$ größerer Modulationsindex und damit ein um den Faktor $10 · \lg \ 9 = 9.54 \ \rm dB$ größerer Störabstand: | ||
| + | :$$G_{\rm FM} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg} | ||
| + | \hspace{0.15cm}(1.5 \cdot 15^2) \hspace{0.15cm}\underline {\approx 25.28\,{\rm dB}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | *Ein weiterer Zugewinn ergibt sich durch den Übergang von $3\ \rm kHz$ auf $1\ \rm kHz$: | ||
| + | :$$G_{\rm FM} (f_{\rm N} = 1\,{\rm kHz}) = 25.28\,{\rm dB} + 9.54\,{\rm | ||
| + | dB}\hspace{0.15cm}\underline {= 34.82\,{\rm dB}} | ||
| + | \hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | '''(3)''' Der maximale Frequenzhub ergibt sich für $f_{\rm N} = B_{\rm NF}$. | ||
| + | *Daraus folgt mit $f_{\rm G} = 3 \ \rm kHz$ und $B_{\rm NF} = 9 \ \rm kHz$: | ||
| + | :$$\Delta f_{\rm A} (B_{\rm NF}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left(\frac{B_{\rm NF}}{f_{\rm G}}\right)^2}} = \sqrt {10} \cdot \Delta f_{\rm A, \hspace{0.08cm}min}= \Delta f_{\rm A, \hspace{0.08cm}max} = 45\,{\rm kHz}$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} \Delta f_{\rm A, \hspace{0.08cm}min} = \frac{45\,{\rm kHz}}{\sqrt {10}}\hspace{0.15cm}\underline {\approx 14.23\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(4)''' Mit der angegebenen Formel erhält man folgende „Gewinne durch Premphase/Deemphase”: | ||
| + | :$$G_{\rm DE} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm | ||
| + | lg}\hspace{0.15cm} \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm | ||
| + | N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) }= 10 \cdot {\rm lg}\hspace{0.15cm} \frac{3^3}{3 \cdot (3 - | ||
| + | 1.249) }\hspace{0.15cm}\underline {\approx 7.1\,{\rm dB}}\hspace{0.05cm},$$ | ||
| + | :$$ G_{\rm DE} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{1^3}{3 \cdot (1 - \pi/4) }\hspace{0.15cm}\underline {\approx 1.9\,{\rm dB}}\hspace{0.05cm},$$ | ||
| + | :$$G_{\rm DE} (f_{\rm N} = 1\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(1/3)^3}{3 \cdot (1/3 - 0.322) }\hspace{0.15cm}\underline {\approx 0.28\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Aufgaben zu Modulationsverfahren|^3.3 Rauscheinfluss bei | + | [[Category:Aufgaben zu Modulationsverfahren|^3.3 Rauscheinfluss bei PM und FM^]] |
Aktuelle Version vom 30. März 2022, 14:41 Uhr
Bei der Sprach– und Tonsignalübertragung wird das Signalfrequenzband vor dem FM–Modulator über ein RC–Hochpassglied gemäß der Skizze vorverzerrt. Man bezeichnet diese Maßnahme als „Preemphase” $\rm (PE)$.
Der Amplitudengang des Preemphase–Netzwerks lautet
- mit den beiden Grenzfrequenzen $f_{\rm G1} = (2π · R_1 · C)^{–1}$ und $f_{\rm G2} = f_{\rm G1}/α_0$, sowie
- dem Gleichsignalübertragungsfaktor $α_0 = R_2/(R_1 + R_2)$:
- $$ |H_{\rm PE} (f)| = \alpha_0 \cdot \sqrt{\frac{1 + (f/f_{\rm G1})^2}{1 + (f/f_{\rm G2})^2}} \hspace{0.05cm}.$$
Für die Praxis kann man davon ausgehen, dass die maximale Nachrichtenfrequenz $f_{\rm N}$ sehr viel kleiner als $f_{\rm G2}$ ist.
Berücksichtigt man weiter, dass der Gleichsignalübertragungsfaktor $α_0$ durch eine Verstärkung um $α$ verändert werden kann, so ist im Weiteren von folgendem Preemphase–Frequenzgang auszugehen $(f_{\rm G} = f_{\rm G1} = 3 \ \rm kHz)$:
- $$|H_{\rm PE} (f)| \approx \alpha \cdot \sqrt{{1 + \left({f}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$
Mit diesem Netzwerk lautet der Frequenzhub $Δf_{\rm A}$ in Abhängigkeit der Nachrichtenfrequenz $f_{\rm N}$:
- $$ \Delta f_{\rm A} (f_{\rm N}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left({f_{\rm N}}/{f_{\rm G}}\right)^2}} \hspace{0.05cm}.$$
- Hierbei ist $Δf_\text{A, min}$ der Frequenzhub für sehr kleine Frequenzen $(f_{\rm N} → 0)$.
- Dieser Parameter ist so zu wählen, dass der maximale Frequenzhub $Δf_\text{A, max}$ nicht größer wird als $45 \ \rm kHz$.
Um das Nutzsignal nicht zu verfälschen, muss diese Vorverzerrung durch ein „Deemphase”–Netzwerk beim Empfänger wieder ausgeglichen werden. Ziel und Zweck von Preemphase/Deemphase ist es allein, die Abhängigkeit des Signal–zu–Rausch–Leistungsverhältnisses von der Signalfrequenz zu vermindern.
In dieser Aufgabe werden folgende Größen verwendet:
- Sinken–SNR bei Zweiseitenband-Amplitudenmodulation $\rm (ZSB–AM)$:
- $$\rho_{{\rm AM} } = \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} } = \xi\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{{\rm AM} } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi \hspace{0.05cm},$$
- Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation $\rm (FM)$ ohne Preemphase/Deemphase:
- $$ \rho_{\rm FM} = {3}/{2 } \cdot \eta^2 \cdot \rho_{\rm AM } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm AM}= 10 \cdot {\rm lg} \hspace{0.15cm}{3}/{2 } \cdot \eta^2 \hspace{0.05cm},$$
- Sinken–SNR und Störabstandsgewinn bei Frequenzmodulation $\rm (FM)$ durch Preemphase/Deemphase:
- $$ \rho_{\rm DE} = \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm DE} = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm DE} - 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{\rm FM}\hspace{0.05cm}$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Rauscheinfluss bei Winkelmodulation.
- Bezug genommen wirdinsbesondere auf den Abschnitt Preemphase und Deemphase.
- Gehen Sie in der gesamten Aufgabe von einem Nachrichtensignal aus, das Frequenzen bis einschließlich $B_{\rm NF}= 9 \ \rm kHz$ beinhaltet.
Fragebogen
Musterlösung
- Der Betragsfrequenzgang des Deemphase–Netzwerks ist wie folgt festgelegt:
- $$ |H_{\rm DE} (f)| = \frac{1}{|H_{\rm PE} (f)|}= \frac{1}{\alpha}\cdot \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}} \hspace{0.05cm}.$$
- Der Frequenzgang eines einfachen RC–Tiefpasses – auch bekannt als Tiefpass erster Ordnung – lautet:
- $$ H_{\rm RC-TP} (f) = \frac{1}{{1 + {\rm j}\cdot f/f_{\rm G}}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} |H_{\rm RC-TP} (f)| = \frac{1}{\sqrt{1 + (f/f_{\rm G})^2}}\hspace{0.05cm}.$$
(2) Die Frequenzmodulation ist auf die maximale Frequenz $B_{\rm NF} = f_\text{N, max}= 9 \ \rm kHz$ ausgelegt. Dann soll der (maximale) Frequenzhub $Δf_{\rm A} = 45\ \rm kHz$ betragen.
- Daraus folgt für den Modulationsindex:
- $$ \eta = \frac{\Delta f_{\rm A}}{f_{\rm N} } = 5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} G_{\rm FM} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 5^2) \hspace{0.15cm}\underline {\approx 15.74\,{\rm dB}} \hspace{0.05cm}.$$
- Mit der Nachrichtenfrequenz $ f_{\rm N} = 3 \ \rm kHz$ ergibt sich ein um den Faktor $3$ größerer Modulationsindex und damit ein um den Faktor $10 · \lg \ 9 = 9.54 \ \rm dB$ größerer Störabstand:
- $$G_{\rm FM} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg} \hspace{0.15cm}(1.5 \cdot 15^2) \hspace{0.15cm}\underline {\approx 25.28\,{\rm dB}} \hspace{0.05cm}.$$
- Ein weiterer Zugewinn ergibt sich durch den Übergang von $3\ \rm kHz$ auf $1\ \rm kHz$:
- $$G_{\rm FM} (f_{\rm N} = 1\,{\rm kHz}) = 25.28\,{\rm dB} + 9.54\,{\rm dB}\hspace{0.15cm}\underline {= 34.82\,{\rm dB}} \hspace{0.05cm}.$$
(3) Der maximale Frequenzhub ergibt sich für $f_{\rm N} = B_{\rm NF}$.
- Daraus folgt mit $f_{\rm G} = 3 \ \rm kHz$ und $B_{\rm NF} = 9 \ \rm kHz$:
- $$\Delta f_{\rm A} (B_{\rm NF}) = \Delta f_{\rm A, \hspace{0.08cm}min} \cdot \sqrt{{1 + \left(\frac{B_{\rm NF}}{f_{\rm G}}\right)^2}} = \sqrt {10} \cdot \Delta f_{\rm A, \hspace{0.08cm}min}= \Delta f_{\rm A, \hspace{0.08cm}max} = 45\,{\rm kHz}$$
- $$\Rightarrow \hspace{0.3cm} \Delta f_{\rm A, \hspace{0.08cm}min} = \frac{45\,{\rm kHz}}{\sqrt {10}}\hspace{0.15cm}\underline {\approx 14.23\,{\rm kHz}}\hspace{0.05cm}.$$
(4) Mit der angegebenen Formel erhält man folgende „Gewinne durch Premphase/Deemphase”:
- $$G_{\rm DE} (f_{\rm N} = 9\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(f_{\rm N}/f_{\rm G})^3}{3 \cdot (f_{\rm N}/f_{\rm G} - \arctan (f_{\rm N}/f_{\rm G}) }= 10 \cdot {\rm lg}\hspace{0.15cm} \frac{3^3}{3 \cdot (3 - 1.249) }\hspace{0.15cm}\underline {\approx 7.1\,{\rm dB}}\hspace{0.05cm},$$
- $$ G_{\rm DE} (f_{\rm N} = 3\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{1^3}{3 \cdot (1 - \pi/4) }\hspace{0.15cm}\underline {\approx 1.9\,{\rm dB}}\hspace{0.05cm},$$
- $$G_{\rm DE} (f_{\rm N} = 1\,{\rm kHz}) = 10 \cdot {\rm lg}\hspace{0.15cm} \frac{(1/3)^3}{3 \cdot (1/3 - 0.322) }\hspace{0.15cm}\underline {\approx 0.28\,{\rm dB}}\hspace{0.05cm}.$$